华为OD技术面试-最短距离矩阵(动态规划、广度优先)
背景
记录2023-10-21 晚华为OD三面的手撕代码题,当时没做出来,给面试官说了我的想法,评价:解法复杂了,只是简单的动态规范 或 广度优先算法,事后找资料记录实现方式。
题目
腐烂的橘子
问题描述:
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
【每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。】
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。【如果不可能,返回 -1。】
示例 1:
输入:[[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:[[2,1,1],[0,1,1],[1 ,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:[[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
实现一(广度优先)
求解思路
就按照题目描述,
(1)按照时间 线
(2)逐步 遍历所有的位置
(3)根据规则,如果有坏橘子,且四个正方向(东南西北)有好橘子,则更新之
(4)设计一个状态变量,记录当前时刻:是否有橘子腐败,如果无橘子腐败,是 全部好,还是全部坏,亦或者 好坏相间。
代码实现
testA = [[2,1,1],[1,1,0],[0,1,1]]
testB = [[2,1,1],[0,1,1],[1,0,1]]
testC = [[0,2]]M_position = testA
print(M_position)row = len(M_position)
col = len(M_position[0])
set_bad = []for ir in range(row):for jc in range(col):if M_position[ir][jc]==1:set_bad.append((ir, jc))
print(row, col)# 一次时间变更
def onetimeupndate():# 状态变量 # 0 无橘子# 1、全部新鲜# (1, 2) 好坏 混杂,且未 感染# 2、全部坏、# 3、坏感染flag = 0# 变更状态的坐标changed_set = []for ir in range(row):for jc in range(col):if M_position[ir][jc]==0:continue# 记录唯一状态if flag!=3:flag = (flag + M_position[ir][jc])/(1 if flag==0 else 2)# 坏橘子才更新if M_position[ir][jc]!=2 or ((ir, jc) in changed_set):continue# 遍历方向for i,j in [[1,0],[0,1],[-1,0],[0,-1]]:ar_, bc_ = ir + i, jc + jif ar_<0 or ar_>=row or bc_<0 or bc_>=col:continueif M_position[ar_][bc_]==1:# 记录更新的坐标changed_set.append((ar_, bc_))# 标记状态flag = 3# 换橘子M_position[ar_][bc_]=2return flagitime = 0
while True:flag = onetimeupndate()print("当前次数",itime)print("状态变量",flag)print("最新结果",M_position)if flag!=3:if 1<flag<2:itime = -1breakitime +=1print("结果",itime)
实现二(动态规范)
求解思路
- 问题抽象为 求每个点 到最近的 坏的橘子的 最短距离
- 构造初始距离矩阵,约定:
0、坏橘子 inf、永远不坏 row*col、好橘子最大距离
- 做两次 扫描,更新最短距离
- 得到整体最短距离,找到 永不更新的点
代码实现
def calmintime(M_position):# 最短路径矩阵M_status = []# 尺寸信息row = len(M_position)col = len(M_position[0])MAXTIME = row * col# 初始矩阵for ir in range(row):for ic in range(col):if ic == 0:M_status.append([])if M_position[ir][ic] == 2: # 腐烂v = 0elif M_position[ir][ic] == 0: # 无v = infelif M_position[ir][ic] == 1: # 新鲜v = MAXTIME # 设为一个到不了的实数最大值M_status[ir].append(v)# 往左下遍历,比较右上两个方向for ir in range(row):for ic in range(col):if M_position[ir][ic]==0:continueif ic-1>=0:if M_status[ir][ic-1]+1<M_status[ir][ic]:M_status[ir][ic] = M_status[ir][ic-1]+1if ir-1>=0:if M_status[ir-1][ic]+1<M_status[ir][ic]:M_status[ir][ic] = M_status[ir-1][ic]+1# 往 右上遍历,比较左下两个方向for ir in reversed(range(row)):for ic in reversed(range(col)):if M_position[ir][ic]==0:continueif ic+1<col:if M_status[ir][ic+1]+1<M_status[ir][ic]:M_status[ir][ic] = M_status[ir][ic+1]+1if ir+1<row:if M_status[ir+1][ic]+1<M_status[ir][ic]:M_status[ir][ic] = M_status[ir+1][ic]+1# 最短距离vlist = []for ir in range(row):for ic in range(col):v = M_status[ir][ic]if not v is inf:vlist.append(v)if len(vlist)==0:return 0vmax = max(vlist)if vmax==MAXTIME: # 还存在新鲜的橘子return -1else:return vmaxtestA = [[2,1,1],[1,1,0],[0,1,1]]
testB = [[2,1,1],[0,1,1],[1,0,1]]
testC = [[0,2]]结果验证

参考资料
矩阵(广度优先搜索)(动态规划)
相关文章:

华为OD技术面试-最短距离矩阵(动态规划、广度优先)
背景 记录2023-10-21 晚华为OD三面的手撕代码题,当时没做出来,给面试官说了我的想法,评价:解法复杂了,只是简单的动态规范 或 广度优先算法,事后找资料记录实现方式。 题目 腐烂的橘子 问题描述ÿ…...

【代码规范】switch 块级的作用域问题
代码规范的一些事儿 问题 今日 Git 提交代码时,出现报错: error Unexpected lexical declaration in case block no-case-declarations 解决过程 我马上就去百度,就找到了这篇文章:解决 Unexpected lexical declaration in ca…...

PHP 基础/练习
练习 成绩定级 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>成绩定级脚本</title> </…...

TCP协议与UDP协议
UDP协议 UDP协议端的格式 16位UDP长度,表示整个数据报(UDP首部UDP数据)的最大长度;如果校验和出错,就会直接丢弃; UDP的特点 UDP传输过程类似寄信 无连接 知道对端的IP和端口号就直接进行传输,不需要建立连接; 不可靠 没有任何安全机制,…...

极智嘉(Geek+)柔性货箱到人拣选方案,助力Starlinks实现高效运营
近些年,电商业务席卷全球,一众企业蓬勃发展。比如沙特阿拉伯先进的物流与供应链解决方案供应商Starlinks的电子商务的销售额从6%增长到了23%。为满足日益增长的国际电商业务需求,以及订单交付时效性更高的要求,Starlinks与全球仓储…...

Hadoop3教程(三十一):(生产调优篇)异构存储
文章目录 (157)异构存储概述概述异构存储的shell操作 (158)异构存储案例实操参考文献 (157)异构存储概述 概述 异构存储,也叫做冷热数据分离。其中,经常使用的数据被叫做是热数据&…...

网络协议--UDP:用户数据报协议
11.1 引言 UDP是一个简单的面向数据报的运输层协议:进程的每个输出操作都正好产生一个UDP数据报,并组装成一份待发送的IP数据报。这与面向流字符的协议不同,如TCP,应用程序产生的全体数据与真正发送的单个IP数据报可能没有什么联…...
vscode摸鱼插件开发
不知道大家在写代码的时候,摸不摸鱼,是不是时不时得打开一下微博,看看今天发生了什么大事,又有谁塌房,而你没有及时赶上。 为此,我决定开发一个vscode插件,来查看微博热搜 插件名称࿱…...
音频录制和处理软件 Audio Hijack mac中文版说明
Audio Hijack mac是一款功能强大的音频录制和处理软件,它可以帮助用户从各种来源捕获和处理音频。 首先,Audio Hijack具有灵活的音频捕获功能。它支持从多个来源录制音频,包括麦克风、应用程序、网络流媒体、硬件设备等等。你可以选择捕获整个…...

寻找二叉树一个节点的后继节点
后继节点:中序遍历的后一个节点 普通二叉树:中序遍历得到一个list,时间复杂度O(n) 本题的二叉树:有父节点的指针,后继节点与原节点的距离为1,因此可以直接通过父节点找到下一个节点 优化:节点…...

如何能够获取到本行业的能力架构图去了解自己的能力缺陷与短板,从而能清晰的去弥补差距?
如何能够获取到本行业的能力架构图去了解自己的能力缺陷与短板,从而能清晰的去弥补差距? 获取并利用能力架构图(Competency Model)来了解自己在特定行业或职位中的能力缺陷和短板,并据此弥补差距,是一个非常…...

红队打靶:Misdirection打靶思路详解(vulnhub)
目录 写在开头 第一步:主机发现与端口扫描 第二步:Web渗透(80端口,战术放弃) 第三步:Web渗透(8080端口) 第四步:sudo bash提权 第五步:/etc/passwd利…...

10.23归并排序
课上 归并排序 最大时,就是两个都是完全倒序,但注意一定有一个序列先用完,此时剩一个序列只有一个元素,不用比较,直接加入,所以就是nn-1, 最小时,是都是完全有序,且一个序列中的元…...
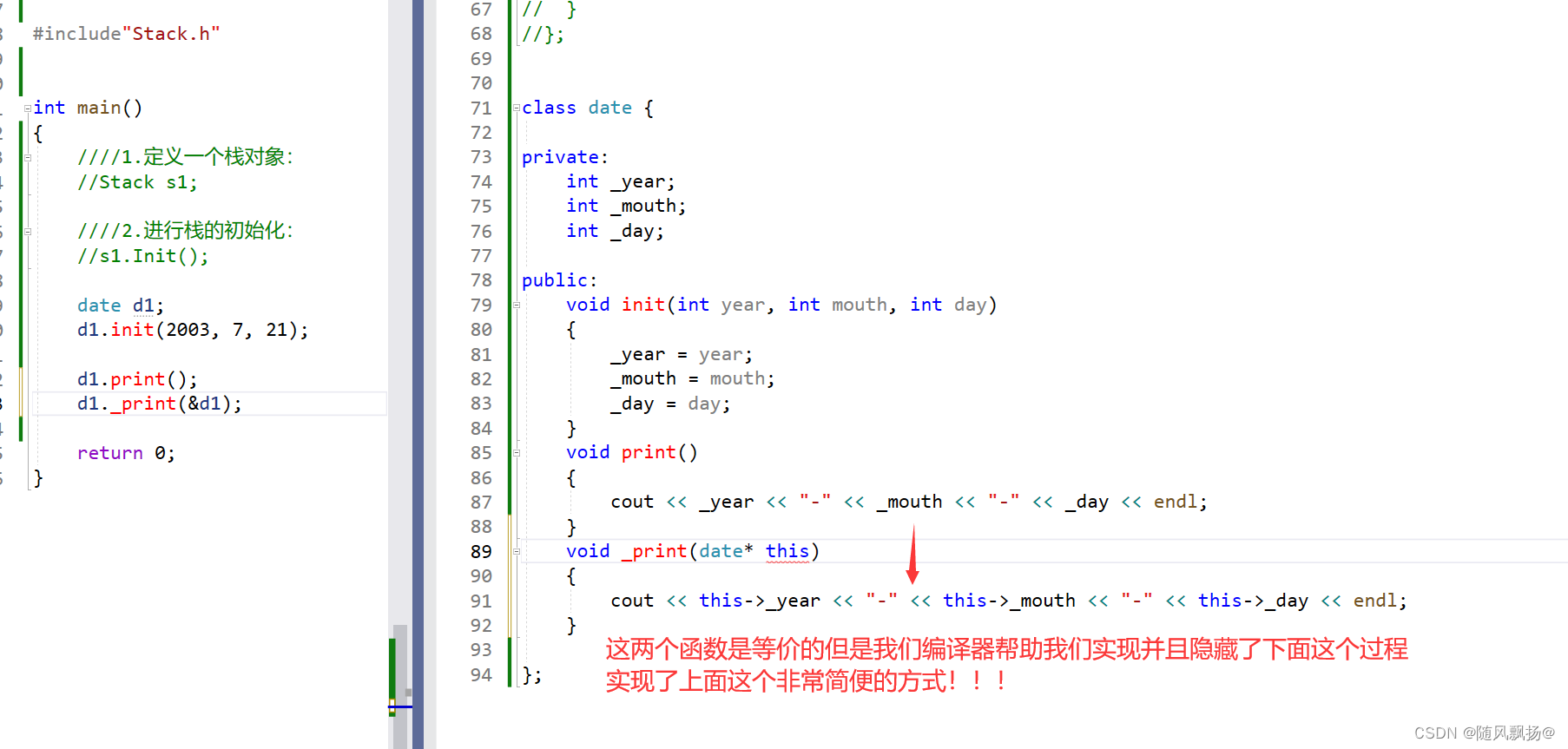
[C++]:2初识C++(auto) + 类和对象上:
[TOC](初识C(auto) 类和对象上) 一.初始C 1.auto关键字:(C11) 1.作为一个变量的类型给这个类型初始化,auto自动识别初始化这个变量值的类型,为auto类型的这个变量开辟一个合适的空间。 补充: 1.typeid(变量名).name—>可以打…...

大学英语试卷
大学英语试卷 If everyone learns to set forth facts and reason things out in social life, many of the contradictions are easy to ____. A. oblige B. engage C. resolve D. commitIf we let the fastest runner set the____, the others will fall behind. A. pace B.…...

SpringBoot Lombok的使用
目录 下载Lombok插件 Lombok的用法 获取日志对象 生成get,set方法 Lombok框架的实现原理 Lombok的常用注解 下载Lombok插件 要使用Lombok首先要确保idea安装了lombok插件 在项目中添加 lombok依赖 在<dependency>里右键生成点击edit starters 插件(没有就下载,可…...

后台管理系统SQL注入漏洞
对于edu来说,是新人挖洞较好的平台,本次记录一次走运的捡漏0x01 前景 在进行fofa盲打站点的时候,来到了一个后台管理处看到集市二字,应该是edu站点 确认目标身份(使用的quake进行然后去ipc备案查询) 网…...

变量常用函数
查看变量类型 type(变量名) 用来查询变量所指的对象类型 >>> a, b, c, d 20, 5.5, True, 43j >>> print(type(a), type(b), type(c), type(d)) <class int> <class float> <class bool> <class complex> 基础数据类型 # coding…...
)
从零学算法(LCR 157)
某店铺将用于组成套餐的商品记作字符串 goods,其中 goods[i] 表示对应商品。请返回该套餐内所含商品的 全部排列方式 。 返回结果 无顺序要求,但不能含有重复的元素。 示例 1: 输入:goods “agew” 输出:[“aegw”,“aewg”,“ag…...

mysql 优化 聚簇索引=主键索引吗
在 InnoDB 引擎中,每张表都会有一个特殊的索引“聚簇索引”,也被称之为聚集索引,它是用来存储行数据的。一般情况下,聚簇索引等同于主键索引,但这里有一个前提条件,那就是这张表需要有主键,只有…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
