最短路相关笔记
Floyd
Floyd 算法,是一种在图中求任意两点间最短路径的算法。
Floyd 算法适用于求解无负边权回路的图。
时间复杂度为 O ( n 3 ) O(n^3) O(n3),空间复杂度 O ( n 2 ) O(n^2) O(n2)。
对于两点 ( i , j ) (i,j) (i,j) 之间的最短路径,有两种可能:从 i i i 直接到 j j j,或者从 i i i 经过若干结点 k k k 到 j j j。
设 f ( k , i , j ) f(k,i,j) f(k,i,j) 为以 k k k 为中转结点时 i i i, j j j 两点间最短路径。
递推转移方程: f ( i , j , k ) = min ( f ( k − 1 , i , j ) , f ( k − 1 , i , k ) + f ( k − 1 , k , j ) ) f(i,j,k)=\min(f(k-1,i,j),f(k-1,i,k)+f(k-1,k,j)) f(i,j,k)=min(f(k−1,i,j),f(k−1,i,k)+f(k−1,k,j))。
滚动数组可以优化为二维数组,即 f ( i , j ) f(i,j) f(i,j)。
核心代码:
for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
预处理操作:
- 将递推数组
memset为无穷大 - 令 f ( i , i ) = 0 f(i,i)=0 f(i,i)=0,即自己和自己距离为 0 0 0
- 读入 ( u , v ) (u,v) (u,v) 之间边权的同时更新 f ( u , v ) f(u,v) f(u,v),无向图无需双向赋值
Dijkstra
单源最短路径问题(SSSP),我们通常使用 Dijkstra 算法。Dijkstra 算法,本质上是使用 BFS 和贪心解决单源图最短路径的问题。虽然但是,Dijkstra 算法不适用于有负边权的图。
所谓单源图,顾名思义,就是规定只有一个起点的图。
对于求解的图,假设任意两顶点之间距离为正无穷。然后开始加入边,更新当前源点与其他顶点的最短距离。将除起点外所有点加入未知集合,并将起点加入已知集合,直至确定该点到起点最短路径;依次更新起点到 i i i 的距离
dis[i],将未知集合dis中与起点距离最小的 x x x 加入已知集合;用 Floyd 的思想,若起点与 n n n 间距离大于起点到 x x x 距离加 x x x 到 n n n 距离,更新dis[n],更新与它相连的点;重复以上步骤直到终点进入已知集合即可。
我们可以用优先队列造小顶堆解决问题。
我们先把每一条边按照举例排序构造小顶堆,然后依次进行操作。
举个栗子,以下图为例:
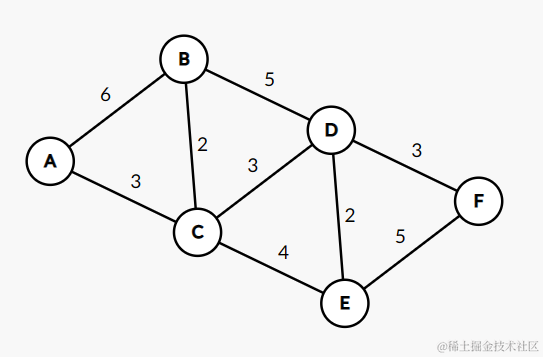
Dijkstra 的基本思想,其实是先把每一个点的 dis 修改为无穷大,然后开始找最小 dis 点,然后枚举以该点为中转点到达的点比较路径长度试图修改。以 A A A 为源点,枚举当前点可以到达的点,第一次我们可以修改 B B B、 C C C 的dis;此时 dis 最小的点为 C C C,所以下一次我们以 C C C 为中转点尝试转移,显然可以改变 dis[D]、dis[E],由于以 C C C 为中转点到 B B B 的距离更优,所以 B B B 也可以被修改,以此类推。
时间复杂度为 O ( m log n ) O(m\log n) O(mlogn), n n n 为顶点数, m m m 为边数。
struct node
{int u,dis;friend bool operator < (node a,node b){return a.dis>b.dis;//小顶堆!}
};priority_queue<node> q;void dij(int s)//s表示源点
{memset(diss,0x7f,sizeof(diss));diss[s]=0;q.push(node{s,0});while(!q.empty()){int u=q.top().id;q.pop();if(vis[u]) continue;vis[u]=1;for(int i=head[u];i;i=nxt[i]){if(diss[to[i]]>diss[u]+w[i]){diss[to[i]]=diss[u]+w[i];q.push(node{to[i],diss[to[i]]});}}}
}
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;const int maxn=2*1e5+5;
int head[maxn],nxt[maxn],to[maxn],w[maxn],cnt,dis[maxn],vis[maxn];void add(int x,int y,int z)
{to[++cnt]=y;w[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}struct node
{int id,dis;friend bool operator < (node a,node b){return a.dis>b.dis;//小顶堆!}
};priority_queue<node> q;void dij(int s)
{memset(vis,0,sizeof(vis));memset(dis,0x3f,sizeof(dis));dis[s]=0;q.push(node{s,0});while(!q.empty()){int u=q.top().id;q.pop();if(vis[u]) continue;vis[u]=1;for(int i=head[u];i;i=nxt[i])if(dis[to[i]]>dis[u]+w[i])dis[to[i]]=dis[u]+w[i],q.push(node{to[i],dis[to[i]]});}
}int main()
{int n,m,s,u,v,w;cin>>n>>m>>s;for(int i=1;i<=m;i++) cin>>u>>v>>w,add(u,v,w);dij(s);for(int i=1;i<=n;i++) cout<<dis[i]<<' ';return 0;
}
SPFA
SPFA 其实是 Bellman-Ford 算法的队列优化算法的别称,常用于求含负边权的单源最短路径(参见 Johnson 算法)以及判负权环。
关于什么是负环,一条边权和为负数的回路就是负环。如果一个点被加入队列的次数大于等于总点数,那么不存在最短路,即一定存在负环。
最坏情况下,SPFA 算法的时间复杂度为 O ( V E ) O(VE) O(VE)(边数 × \times ×点数)。
SPFA 的流程为,每次从队列中取出队首点,尝试更新与这个点相连的点的 dis,若可以更新就将其入队。
代码如下:
void spfa()
{memset(dis,0x3f3f3f,sizeof(vis));dis[s]=0;z[top=1]=s;for(int j=1;j<=top;j++){int now=z[j];vis[now]=0;for(int head[now];i;i=nxt[i])if(dis[to[i]]>dis[now]+w[i]){dis[to[i]]=dis[now]+w[i];if(!vis[to[i]]) vis[to[i]]=1,z[++top]=to[i];}}
}
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;const int maxn=40005;
int nxt[maxn],to[maxn],head[maxn],val[maxn],dis[maxn],vis[maxn],rec[maxn],cnt,n,m;
queue<int> q;void add(int x,int y,int z)
{to[++cnt]=y;val[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}bool spfa()
{memset(dis,127,sizeof(dis));memset(vis,0,sizeof(vis));memset(rec,0,sizeof(rec));while(!q.empty) q.pop();q.push(1);dis[1]=0,vis[1]=1,rec[1]++;while(!q.empty()){int u=q.front();q.pop();vis[u]=0;//队首已出队for(int i=head[u];i;i=nxt[i]){if(dis[to[i]]>dis[u]+val[i]){dis[to[i]]=dis[u]+val[i];//对于判断是否有负环,用数组rec记录点的入队次数,如果入队次数>n,就证明出现了负环导致没有最短路if(!vis[to[i]]) vis[to[i]]=true,rec[to[i]]++,q.push(to[i]);//能更新,压入队列if(rec[to[i]]>=n) return true;}} }return false;
}int main()
{int T,u,v,w;cin>>T;while(T--){cin>>n>>m;memset(head,0,sizeof(head));cnt=0;for(int i=1;i<=m;i++){cin>>u>>v>>w;add(u,v,w);if(w>=0) add(v,u,w);}if(spfa()) cout<<"YES"<<endl;else cout<<"NO"<<endl;}return 0;
}
Johnson
Johnson 全源最短路算法,顾名思义就是一个名为 Johnson 的大神发明的一种求全源最短路的算法。可以解决图中任意起点的最短路问题。
首先考虑一种逆天的朴素做法,每次取一个点去跑 SPFA,时间复杂度 O ( m n 2 ) O(mn^2) O(mn2)(点数 × \times × 边数);或者干脆直接跑 O ( n 3 ) O(n^3) O(n3) 的 Floyd。显然这都是会炸掉的。
所以我们考虑一种很强的单源最短路径算法——Dijkstra。但是 Dijkstra 不能解决负边权,怎么办?
第一反应是把所有边的边权都加上一个数使其非负,但是显然可以被 Hack 掉:
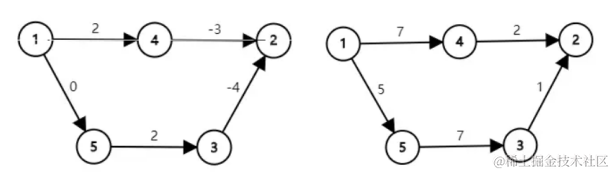
对于上图,我们惊奇地发现,原先 1 1 1 到 2 2 2 的最短路是 1 → 5 → 3 → 2 1\rightarrow5\rightarrow3\rightarrow2 1→5→3→2,结果变成正的之后最短路变成 1 → 4 → 2 1\rightarrow4\rightarrow2 1→4→2 了,寄。
Johnson 算法登场!它是一种可以替代上面逆天的负边权转正方法的算法。
我们新建一个虚拟节点编号为 0 0 0,这个点向其他所有点都连一条边权为 0 0 0 的边。然后跑一遍 SPFA,统计 0 0 0 到所有其他结点的最短路长度 h i h_i hi(为什么叫 h h h 是因为《算法导论》里这么叫)。如果存在一条边 u → v u\rightarrow v u→v 边权为 w w w,那么将该边边权重新设置为 w + h u − h v w+h_u-h_v w+hu−hv。
重新设置边权之后,我们就可以对于每一个节点跑一遍 Dijkstra 了。总时间复杂度 O ( n m log m ) O(nm\log m) O(nmlogm)。
如何证明 Johnson 算法的正确性?
首先我们证明经过这样一波操作之后最短路不会变。对于原最短路 s → p 1 → p 2 → ⋯ → p k → t s\rightarrow p_1\rightarrow p_2\rightarrow\cdots\rightarrow p_k\rightarrow t s→p1→p2→⋯→pk→t,用 Johnson 算法改变边权之后的长度可以表示为 ( w ( s , p 1 ) + h s − h p 1 ) + ( w ( p 1 , p 2 ) + h p 1 − h p 2 ) + ⋯ + ( w ( p k , t ) + h p k − h t ) (w(s,p_1)+h_s-h_{p_1})+(w(p_1,p_2)+h_{p_1}-h_{p_2})+\cdots+(w(p_k,t)+h_{p_k}-h_t) (w(s,p1)+hs−hp1)+(w(p1,p2)+hp1−hp2)+⋯+(w(pk,t)+hpk−ht),化简之后为 w ( s , p 1 ) + w ( p 1 , p 2 ) + ⋯ + w ( p k , t ) + h s − h t w(s,p_1)+w(p_1,p_2)+\cdots+w(p_k,t)+h_s-h_t w(s,p1)+w(p1,p2)+⋯+w(pk,t)+hs−ht。如果原先的 s → t s\rightarrow t s→t 为最短路,那么更改之后其实就是加了个 h s − h t h_s-h_t hs−ht,因为这个 h s − h t h_s-h_t hs−ht 是定值,所以说原先的最短路和改变边权之后的最短路显然是一条路径因为原先要经过的点必须经过而无论中间取什么点都不可能改变加上的 h s − h t h_s-h_t hs−ht 的值,所以在新图上我们跑 Dijkstra 得到的最短路经过的点一定和原图相同。
接下来证明为什么边权处理之后一定非负。对于图中任意一条边 ( u , v ) (u,v) (u,v),一定满足 h v ≤ h u + w ( u , v ) h_v\leq h_u+w(u,v) hv≤hu+w(u,v),这是显然的,因为从 0 0 0 到 v v v 的最短路不可能超过从 0 0 0 到 u u u 的最短路加上 ( u , v ) (u,v) (u,v) 的边权,否则就会被松弛更新,其实这就是图论中的三角形不等式,最短路上的所有边都满足三角形不等式。于是乎用 Johnson 算法更改后的边权 w ′ ( u , v ) = w ( u , v ) + h u − h v w'(u,v)=w(u,v)+h_u-h_v w′(u,v)=w(u,v)+hu−hv 一定是非负的,完结撒花!
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define int long longconst int maxn=9005,maxx=1e9;//注意原有m条边+新建0节点n条边,数组小了会炸
int nxt[maxn],head[maxn],cnt,to[maxn],w[maxn],h[maxn],vis[3005],tim[3005],m,n,u,v,ww,dis[3005];void add(int x,int y,int z)
{to[++cnt]=y;w[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}bool spfa()//SPFA判负环
{queue<int> q;memset(h,127/3,sizeof(h));h[0]=0,vis[0]=1;q.push(0);while(!q.empty()){int u=q.front();q.pop();vis[u]=0;for(int i=head[u];i;i=nxt[i]){int v=to[i];if(h[v]>h[u]+w[i]) {h[v]=h[u]+w[i];if(!vis[v]) {q.push(v),vis[v]=1,tim[v]++;if(tim[v]>n) return true;}}}}return false;
}struct node
{int id,dis;bool friend operator < (node a,node b){return a.dis>b.dis;}
};void dij(int s)
{priority_queue<node> q;memset(vis,0,sizeof(vis));for(int i=1;i<=n;i++) dis[i]=maxx;dis[s]=0;q.push(node{s,0});while(!q.empty()){int u=q.top().id;q.pop();if(vis[u]) continue;vis[u]=1;for(int i=head[u];i;i=nxt[i])if(dis[to[i]]>dis[u]+w[i])dis[to[i]]=dis[u]+w[i],q.push(node{to[i],dis[to[i]]});}
}signed main()
{cin>>n>>m;for(int i=1;i<=m;i++) cin>>u>>v>>ww,add(u,v,ww);for(int i=1;i<=n;i++) add(0,i,0);if(spfa()) cout<<-1,exit(0);for(int u=1;u<=n;u++) for(int i=head[u];i;i=nxt[i]) w[i]+=h[u]-h[to[i]];for(int i=1;i<=n;i++){dij(i);int ans=0;for(int j=1;j<=n;j++){if(dis[j]==maxx) ans+=j*maxx;else ans+=j*(dis[j]+h[j]-h[i]);}cout<<ans<<endl;}return 0;
}
总结
(下表中 m m m 为边数, n n n 为点数)
| 最短路算法 | Floyd | SPFA | Dijkstra | Johnson |
|---|---|---|---|---|
| 最短路类型 | 每对结点之间的最短路 | 单源最短路 | 单源最短路 | 每对结点之间的最短路 |
| 适配的图 | 任意图 | 任意图 | 非负权图 | 任意图 |
| 能否检测负环 | 能 | 能 | 不能 | 能 |
| 时间复杂度 | O ( n 3 ) O(n^3) O(n3) | O ( n m ) O(nm) O(nm) | O ( m log m ) O(m\log m) O(mlogm) | O ( n m log m ) O(nm\log m) O(nmlogm) |
相关文章:

最短路相关笔记
Floyd Floyd 算法,是一种在图中求任意两点间最短路径的算法。 Floyd 算法适用于求解无负边权回路的图。 时间复杂度为 O ( n 3 ) O(n^3) O(n3),空间复杂度 O ( n 2 ) O(n^2) O(n2)。 对于两点 ( i , j ) (i,j) (i,j) 之间的最短路径,有…...

Web前端-Vue2+Vue3基础入门到实战项目-Day5(自定义指令, 插槽, 案例商品列表, 路由入门)
自定义指令 基本使用 自定义指令: 自己定义的指令, 可以封装一些dom操作, 扩展额外功能全局注册// 1. 全局注册指令 Vue.directive(focus, {// inserted 会在 指令所在的元素, 被插入到页面中时触发inserted (el) {// el 就是指令所绑定的元素// console.log(el)el.focus()} …...

mysql json数据类型 相关函数
创建JSON文本的函数 1.JSON_ARRAY(转换json数组) 2.JSON_OBJECT(转换json对象) 3.JSON_QUOTE(转义字符串) 搜索JSON文本的函数 1.JSON_CONTAINS(json当中是否包含指定value) 2.J…...

如何实现前端实时通信(WebSocket、Socket.io等)?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

使用 SSSD 进行网络用户身份验证
文章目录 使用 SSSD 进行网络用户身份验证SSSD和Active Directory先决条件、假设和要求软件安装加域 SSSD配置自动创建HOME目录 检查和验证 Kerberos票证已知的问题参考 使用 SSSD 进行网络用户身份验证 SSSD 代表系统安全服务守护程序,它实际上是处理来自各种网络…...

紫光展锐携中国联通完成RedCap芯片V517孵化测试
近日,紫光展锐携手中国联通5G物联网OPENLAB开放实验室(简称“OPENLAB实验室”)共同完成RedCap芯片V517创新孵化,并实现在联通5G全频段3.5GHz、2.1GHz、900MHz下的端到端业务验证测试。 V517是一款基于紫光展锐5G成熟平台设计与研发…...

算法通关村第十一关青铜挑战——移位运算详解
大家好,我是怒码少年小码。 计算机到底是怎么处理数字的? 数字在计算机中的表示 机器数 一个数在计算机中的二进制表示形式,叫做这个数的机器数。 机器数是带符号的,在计算机用一个数的最高位存放符号,正数为0&am…...

2023年面试测试工程师一般问什么问题?
面试和项目一起,是自学路上的两大拦路虎。面试测试工程师一般会被问什么问题,总结下来一般是下面这4类: 1.做好自我介绍 2.项目相关问题 3.技术相关问题 4.人事相关问题 接下来,主要从以上四个方向分别展开介绍。为了让大家更有获…...
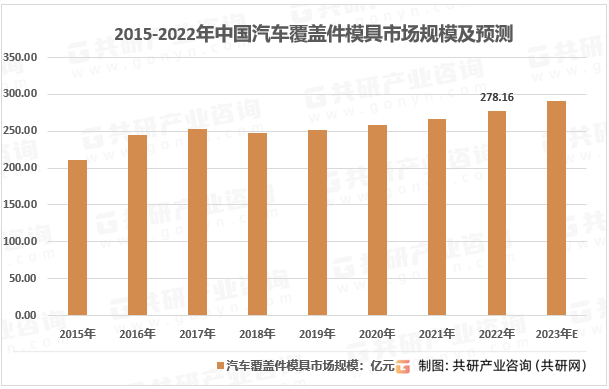
2023年中国汽车覆盖件模具竞争格局、市场规模及行业需求前景[图]
汽车覆盖件模具是汽车车身生产的重要工艺装备,其设计和制造时间约占汽车开发周期的 2/3,是汽车换型的重要制约因素之一。汽车覆盖件模具具有尺寸大、工作型面复杂、技术标准高等特点,属于技术密集型产品。汽车覆盖件模具按以其冲压的汽车覆盖…...
vue3项目运行报错import zhCn from “element-plus/lib/locale/lang/zh-cn“
解决办法 import zhCn from "element-plus/lib/locale/lang/zh-cn";修改为 import zhCn from "element-plus/dist/locale/zh-cn.mjs";...
、条款27(禁止部分隐式生成的函数))
读书笔记:Effective C++ 2.0 版,条款26(歧义)、条款27(禁止部分隐式生成的函数)
条款26: 当心潜在的歧义 即使cpp支持潜在二义性/歧义,也不要使用。 void f(int); void f(char); double d 6.02; f(d); //需要明确转换多继承充满了潜在二义性/歧义的可能。 class Base1 {public: int doIt();}; class Base2 {public: void doIt();}; class Deri…...

MySQL基本操作之数据库设计理论
1、数据的设计准则 1)糟糕的数据库设计表现在以下几个方面: 访问数据效率低下存在大量的数据冗余,浪费存储空间更新和检索数据时会出现许多问题2)良好的数据库设计表现在以下几方面: 访问效率高减少数据冗余,节省存储空间便于进一步扩展可以使应用程序的开发变得更容易…...
)
SpringBoot的日志系统(日志分组、文件输出、滚动归档)
[toc](目录) > SpringBoot3需要jdk17 # 1. 简介 1. Spring5及以后Spring自己实现了commons-logging,来作为内部的日志。日志的jar包是org.springframework:spring-jcl:6.0.10。查看org.apache.commons.logging.LogAdapter Java package org.apache.commons.log…...
一种基于HTTPS实现的Web账号登录Linux桌面系统的实现方案
问题由来 客户需求计划列入支持第三方帐号系统,包括Web账号。需求来源是用户想要用它们的帐号直接登录Linux Deepin操作系统。一个失败的实现方案是用户以较小的成本改造帐号管理系统发布HTTP服务,我们开发一个PAM模块与Web服务器交互,数据格…...

【Linux】psplash制作Linux开机动画
1. 下载psplash软件 下载psplash源码到ubuntu中: 下载地址:https://git.yoctoproject.org/psplash/commit/安装依赖环境 sudo apt-get install libgdk-pixbuf2.0-dev2. 准备图片 开机动画静态图片:psplash-poky.png开机动画进度条图片&…...

WMS透明仓库:实现仓储的全方位可视化与优化
一、WMS透明仓库的定义与特点 1. WMS透明仓库的定义:WMS透明仓库是一种基于信息技术的仓库管理系统,通过实时数据采集、分析和可视化,将仓库内外的物流流程、库存状态、人员活动等信息以透明的方式展示给相关利益方。 2. 实时数据采集&…...

软考系统架构师知识点集锦一:系统工程与信息系统基础
一、考情分析 二、考点精讲 2.1 软件开发方法 (1)结构化开发方法 用户至上,自顶向下,逐步分解(求解),严格区分工作阶段,每阶段有任务与成果,强调系统开发过程的整体性和全局性,系统开发过程工…...

建筑模板常见的问题有哪些?
在建筑模板的使用过程中,常见的问题包括以下几个方面:1. 模板质量问题: - 模板破损或变形:模板可能在运输、安装或使用过程中受到损坏,如裂缝、断裂或变形。这可能导致模板的稳定性和承载能力下降。 - 模板尺寸不准确&…...
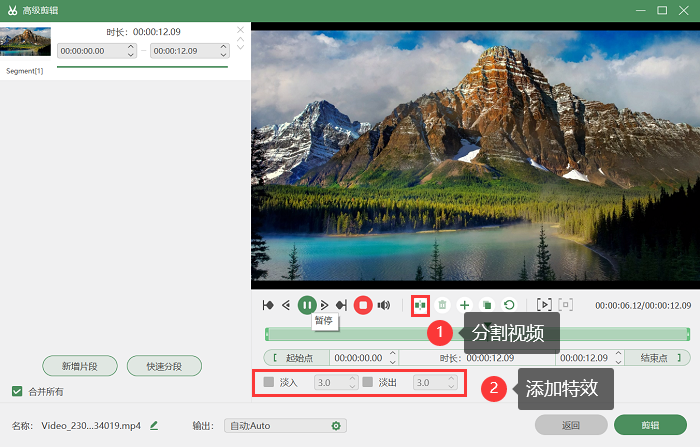
windows11录屏功能详解,记录你的精彩时刻
windows 11是微软最新推出的操作系统版本,拥有很多简单便捷的功能,包括内置的录屏工具,让用户可以轻松地录制屏幕内容。但是很多人不了解windows11录屏功能,本文将详细介绍windows 11录屏的三个方法,以及它们的优势和适…...

重入漏洞Victim
重入漏洞 顾名思义,重入漏洞可以简单理解为“重新进入的漏洞”。举个简单的例子,你往某个合约里存入了1个Ether,然后点击退款,按理来说只能退一个Ether,但是可以利用重入漏洞反复退款,把合约里的Ether掏空…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
