Tomcat及jdk安装下载及环境配置(超超超详解)
我是看了两篇博客安装配置好的
jdk
最详细jdk安装以及配置环境(保姆级教程)_安装jdk需要配置环境变量吗-CSDN博客
tomcat
Tomcat的下载安装与配置及常见问题处理【Win11】 - 鞠雨童 - 博客园 (cnblogs.com)
本篇文章是我解决了很多朋友的tomcat配置问题总结的下载配置具体步骤和问题发生的原因
目录
1.安装最新版本jdk,环境变量配置
2.tomcat下载及环境配置
打开tomcat测试是否成功
关于闪退问题
1.安装最新版本jdk,环境变量配置
下载网址:Java Downloads | Oracle 中国
 下载好包以后就双击安装,选择自己想要安装的位置,环境变量配置
下载好包以后就双击安装,选择自己想要安装的位置,环境变量配置
新建环境变量

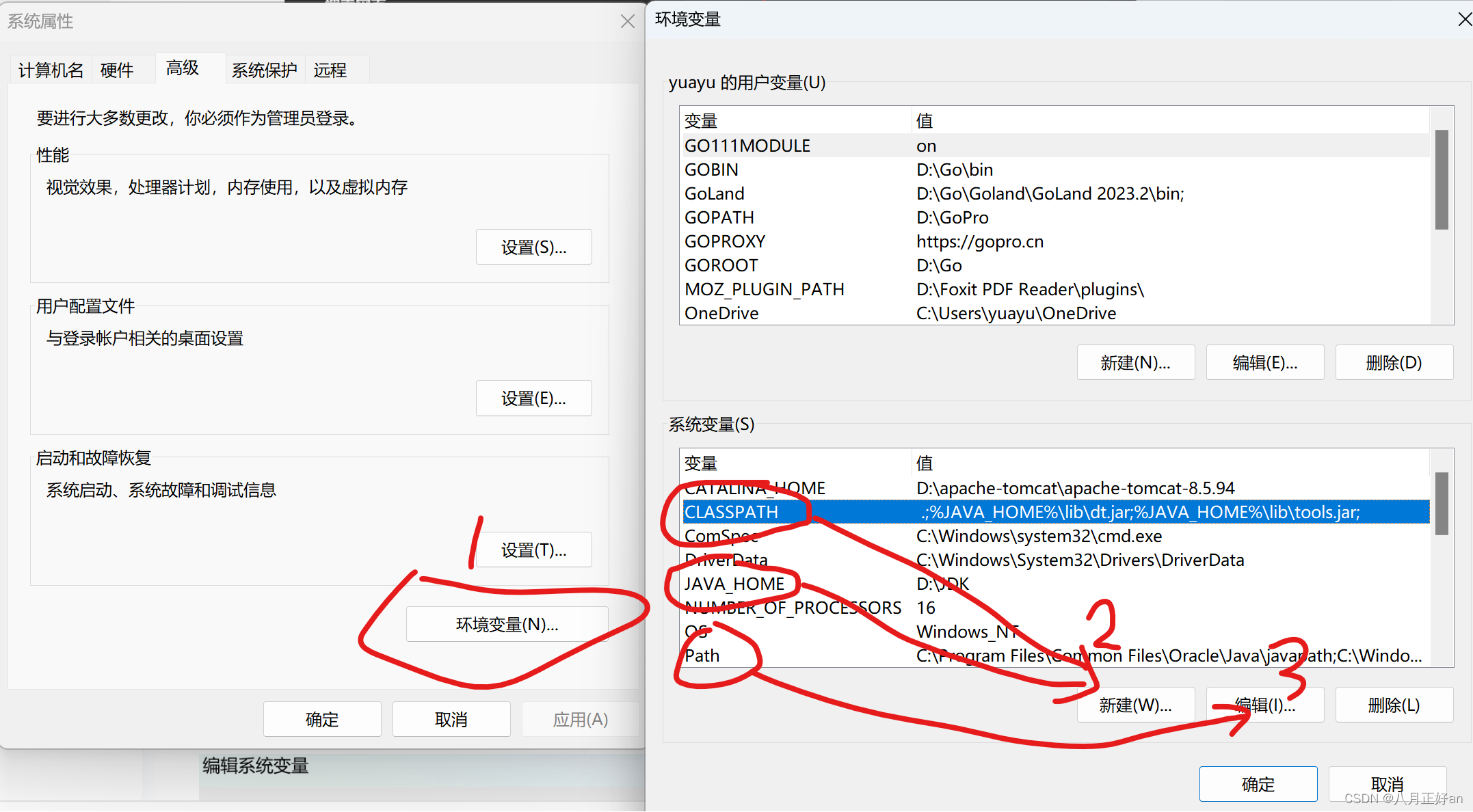
变量名JAVA_HOME 变量值 jdk安装的位置(可以看见bin目录的目录地址)
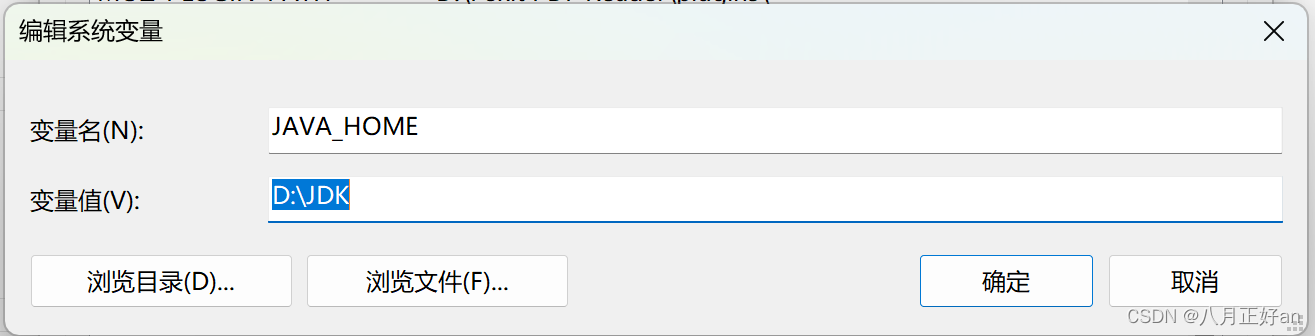

变量名 CLASSPATH 变量值 .;%JAVA_HOME%\lib\dt.jar;%JAVA_HOME%\lib\tools.jar;

(ps:有不会的看这个博客,我己经安装过了)最详细jdk安装以及配置环境(保姆级教程)_安装jdk需要配置环境变量吗-CSDN博客
2.tomcat下载及环境配置
官网下载:Apache Tomcat® - Welcome!

下载好以后就解压到一个你喜欢的位置就可以了,我是解压后挪到D盘了安装位置如下

接下来是环境配置

1点击环境变量,在系统变量下点击新建,变量为CATALINA_HOME ,值为tomcat-能看到bin目录的目录地址(如下图所示),点击复制以后粘贴到值中,再按确定就好了


修改Path的值
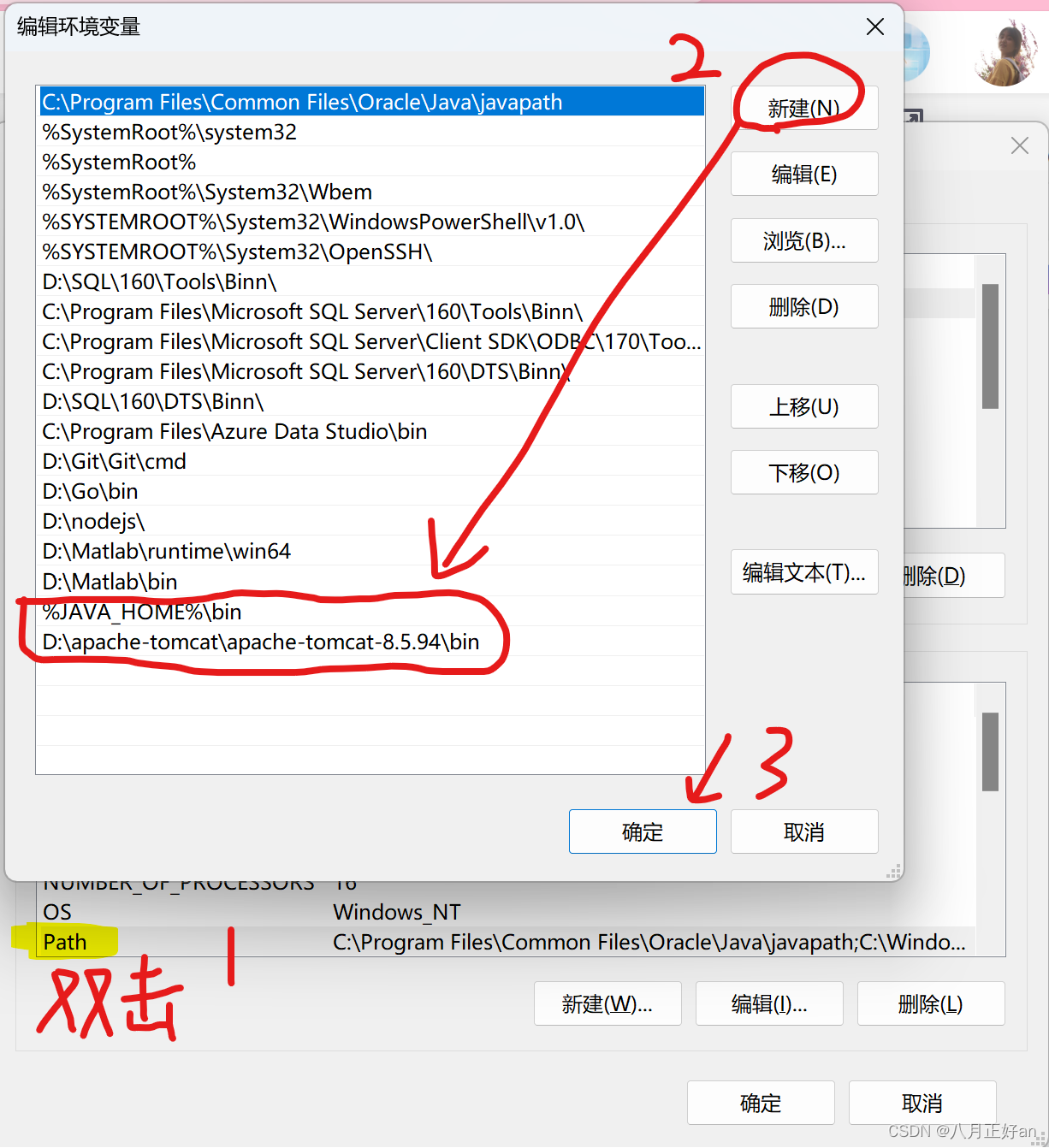
到这里环境就配置好了
打开tomcat测试是否成功
打开所下载的tomcat的bin目录,找到startup.bat--windows批处理文件,双击

出现如下的这个界面并且不闪退,则说明已经打开了tomcat的服务器

打开你常用的浏览器,输入网址:http://localhost:8080/,如果打开是如下界面,说明你已经完美地完成了环境配置!!!可以畅意地书写代码了
关于闪退问题
如出现闪退,我见过的最多的原因就是jdk的问题,你可以先检查jdk是不是最新版本,然后再检查环境变量是否配置正确(参考我前面的配置教程)只要jdk是最新版本,且环境参数也配置正确没见过这个startup打不开的,所以如果还是闪退就好好检查版本和环境参数,一步一步按照我的步骤来一定可以配置好的!!有问题欢迎留言
相关文章:

Tomcat及jdk安装下载及环境配置(超超超详解)
我是看了两篇博客安装配置好的 jdk 最详细jdk安装以及配置环境(保姆级教程)_安装jdk需要配置环境变量吗-CSDN博客 tomcat Tomcat的下载安装与配置及常见问题处理【Win11】 - 鞠雨童 - 博客园 (cnblogs.com) 本篇文章是我解决了很多朋友的tomcat配置问题总…...
专业安卓实时投屏软件:极限投屏(QtScrcpy作者开发)使用说明
基本介绍 极限投屏是一款批量投屏管理安卓设备的软件,是QtScrcpy作者基于QtScrcpyCore开发,主要功能有: 设备投屏&控制:单个控制、批量控制分组管理wifi投屏adb shell快捷指令文件传输、apk安装 更多功能还在持续更新。 极…...
C++:二叉搜索树的原理和模拟实现
文章目录 二叉搜索树二叉搜索树的基本实现原理 二叉搜索树的实现非递归版本的实现递归版本的实现 二叉搜索树 二叉搜索树也叫做二叉排序树,可以是空树,也可以是满足一些要求的二叉树 若它的左子树不为空,则左子树上所有节点的值都小于根节点…...
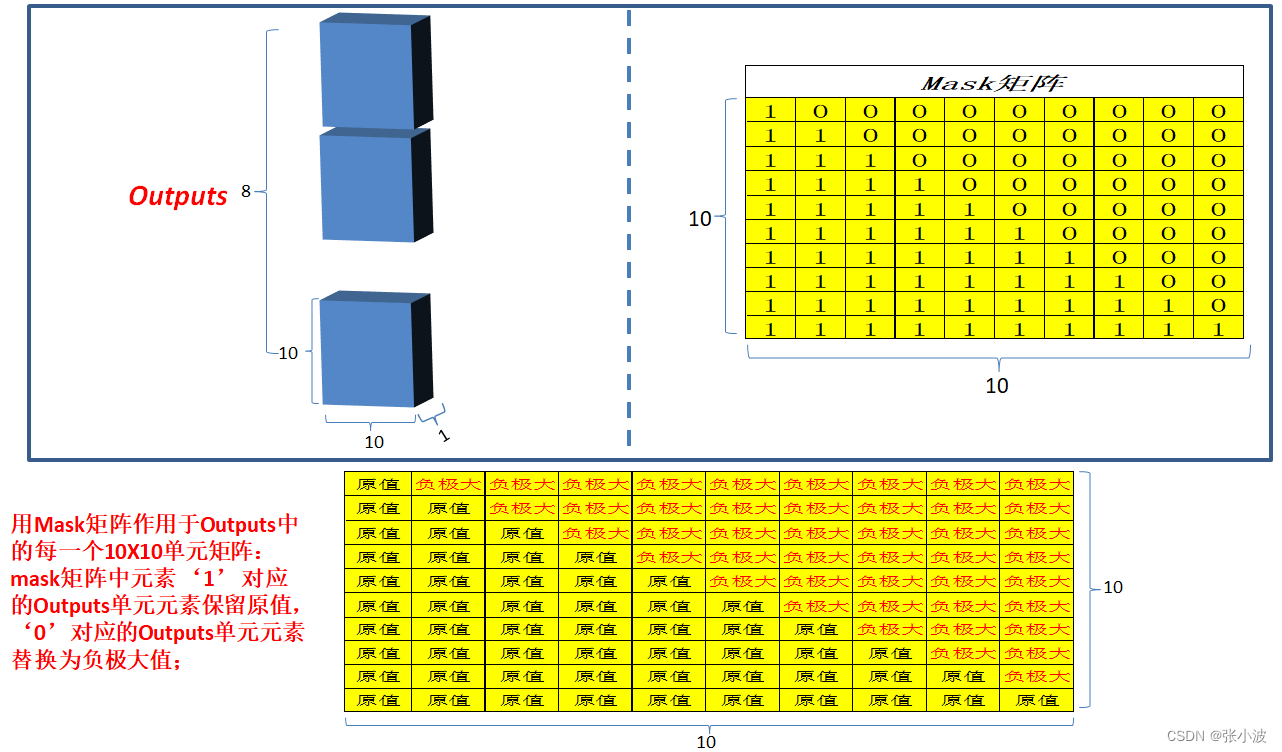
学习视觉CV Transformer (2)--Transformer原理及代码分析
下面结合代码和原理进行深入分析Transformer原理。 2 Transformer深入分析 对于CV初学者来说,其实只需要理解Q K V 的含义和注意力机制的三个计算步骤: Q 和所有 K 计算相似性;对相似性采用 Softmax 转化为概率分布;将概率分布…...

【AI视野·今日CV 计算机视觉论文速览 第271期】Thu, 19 Oct 2023
AI视野今日CS.CV 计算机视觉论文速览 Thu, 19 Oct 2023 Totally 63 papers 👉上期速览✈更多精彩请移步主页 Daily Computer Vision Papers Learning from Rich Semantics and Coarse Locations for Long-tailed Object Detection Authors Lingchen Meng, Xiyang D…...
GoLong的学习之路(四)语法之循环语句
书接上回,上回说到运算符,这次我们说一个编程语言中最重要的一点:流程控制,及循环语句 文章目录 循环语句if else(分支结构)if条件判断特殊写法 for(循环结构)for range(键值循环) switch casegoto(跳转到指定标签)break(跳出循环…...
【Lua语法】字符串
Lua语言中的字符串是不可变值。不能像在C语言中那样直接改变某个字符串中的某个字符,但是可以通过创建一个新字符串的方式来达到修改的目的 print(add2(1 , 2 ,15,3))a "no one"b string.gsub(a , "no" , "on1111")print(a) print…...

程序员节的由来
早在2006年的时候 我就发现了 1024KB1MB 然后恰好又是2的10次方 那时候我就把这一天定义为程序员节了 不过当时并没有太多的知名度。 所以严格意义来讲 距历史记载,程序员应该是由我(田尚滨/cagy)发明的。 As early as 2006 I found …...
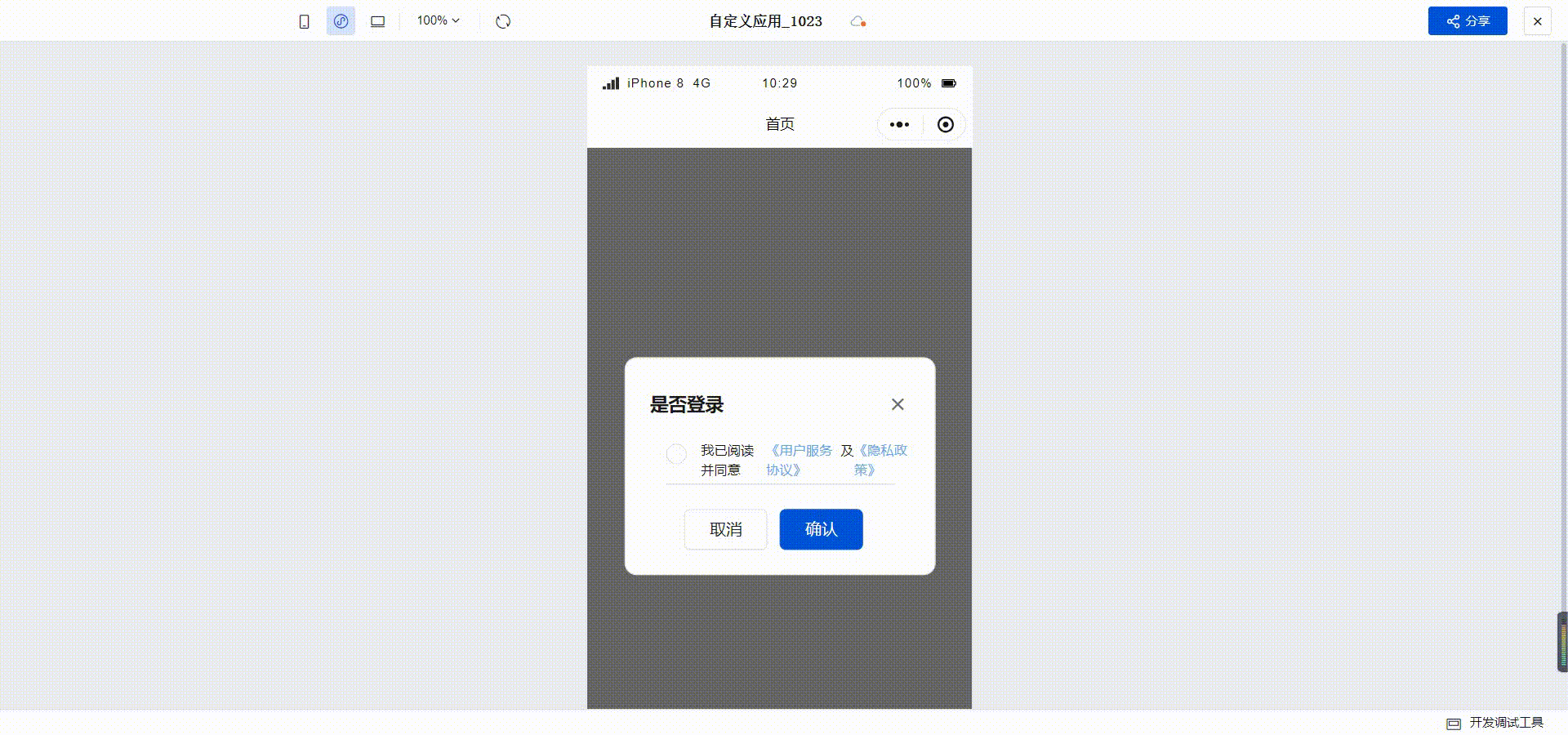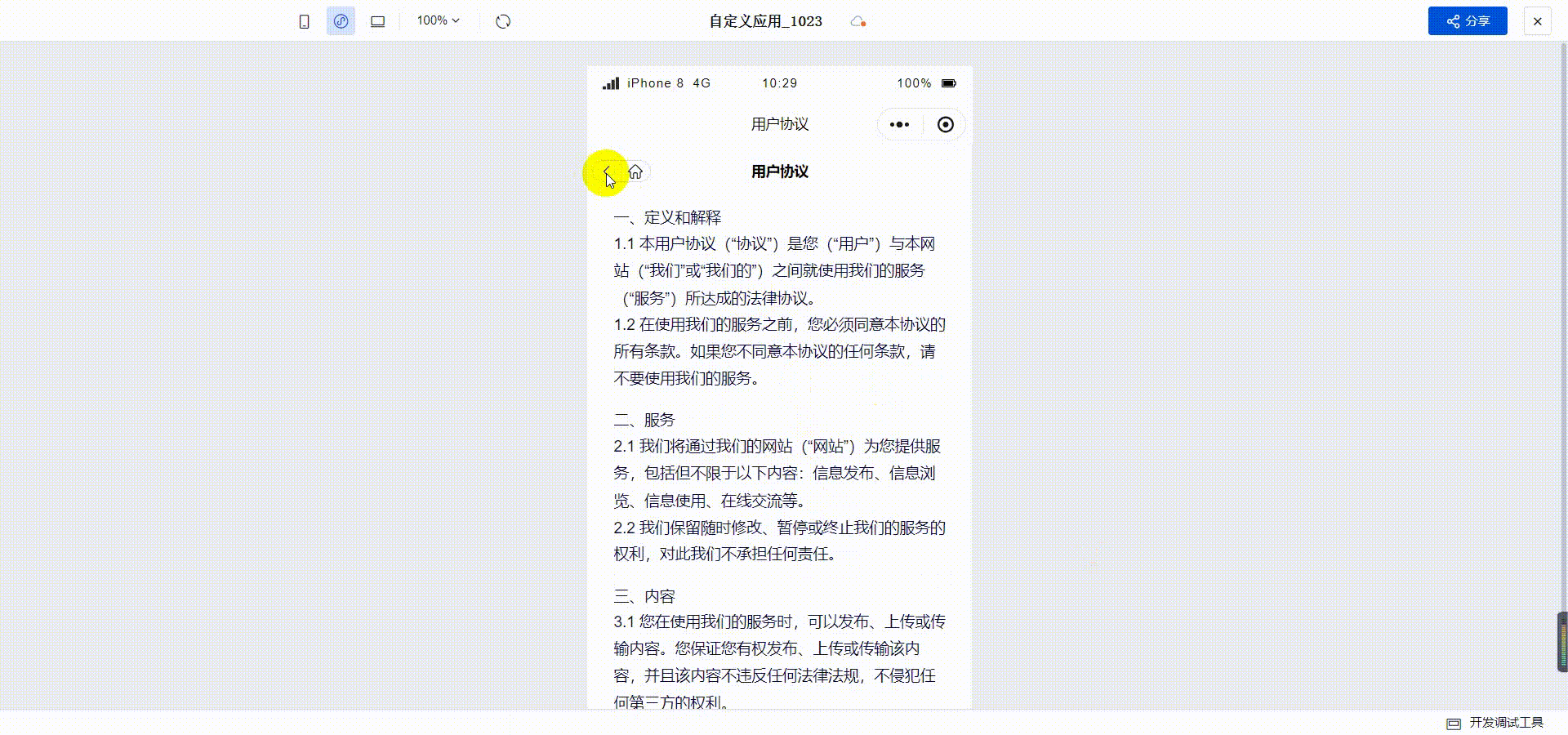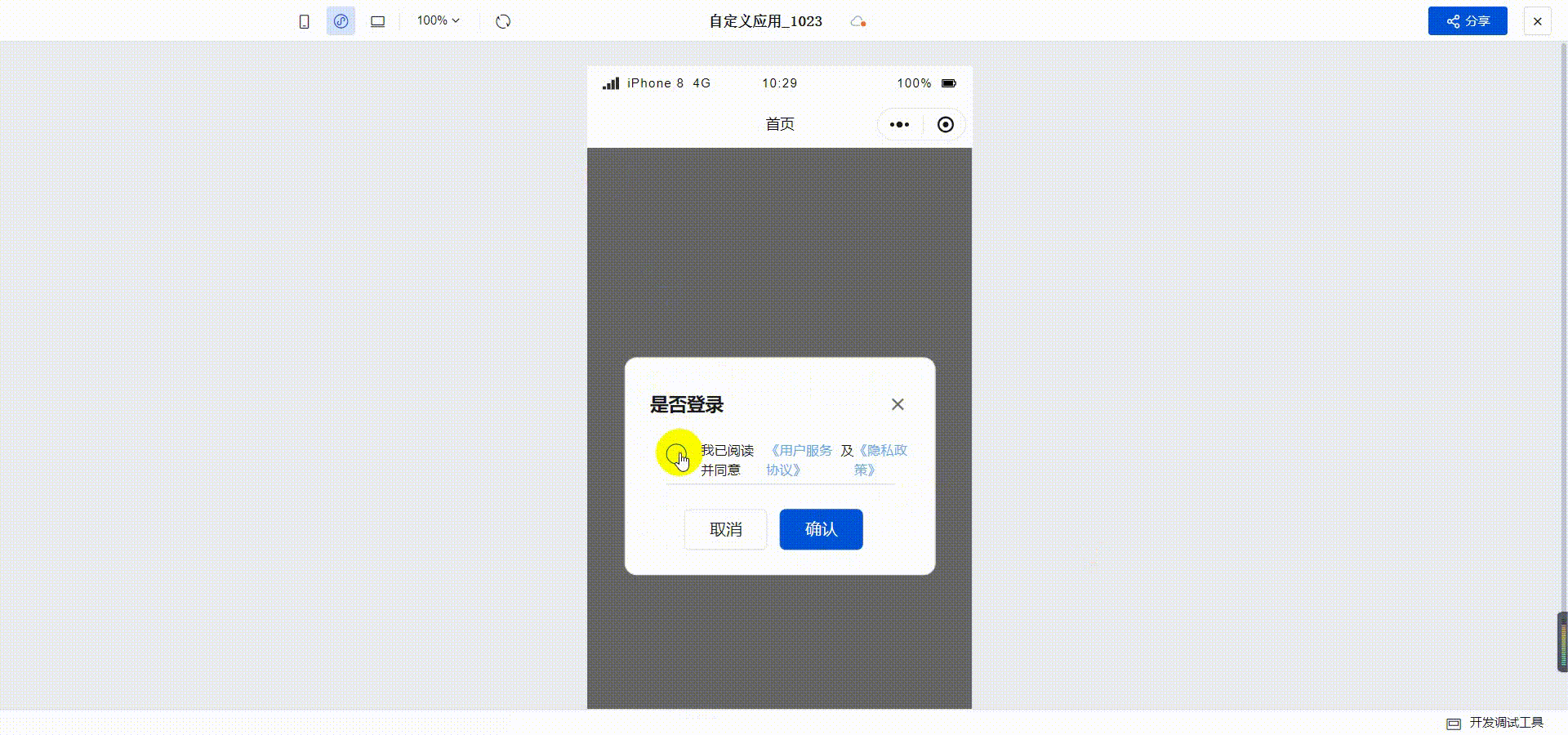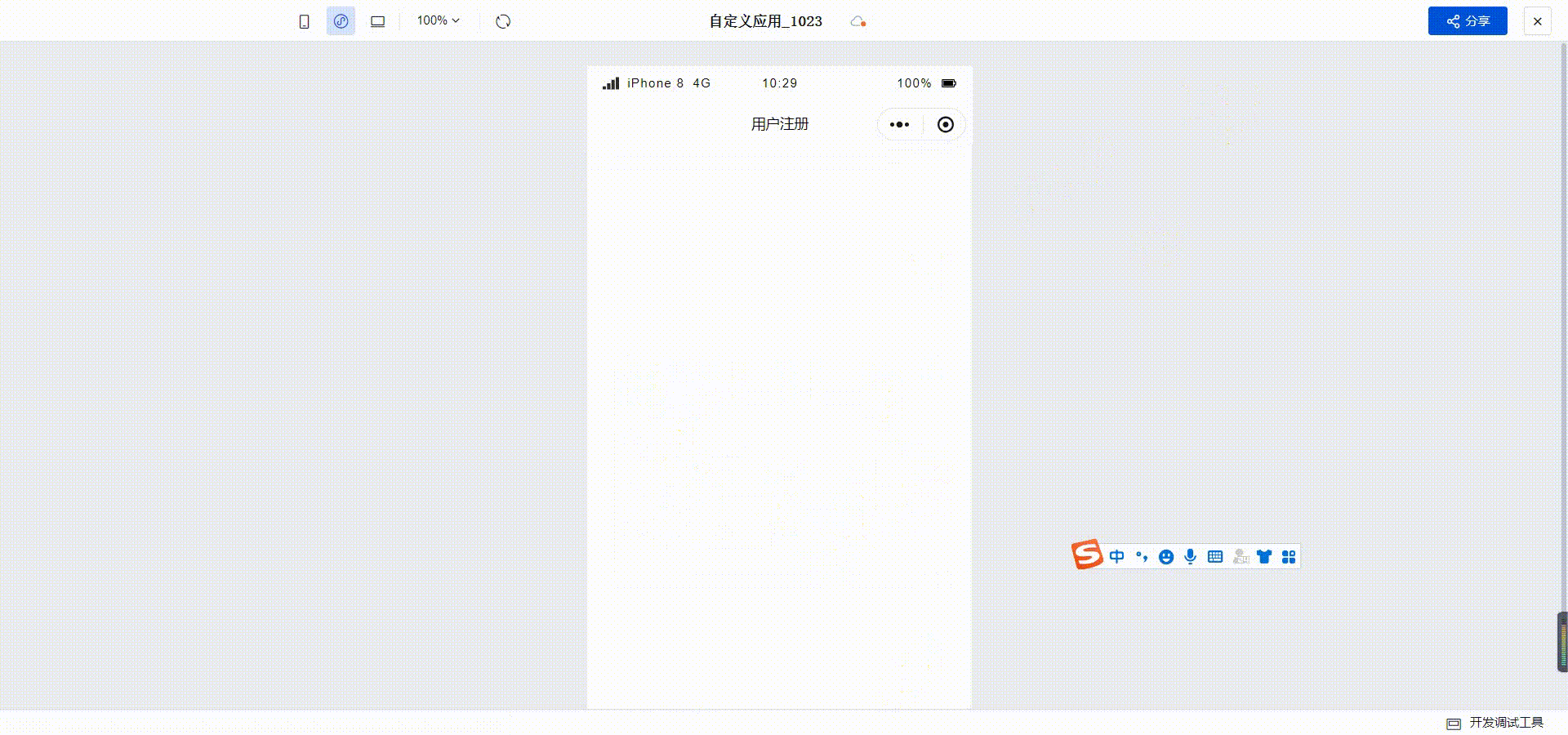
订水商城H5实战教程-03用户协议
目录 1 创建页面2 为文本组件增加事件3 检查用户协议是否勾选最终效果 我们上一篇介绍了打开首页时弹出登录窗口的功能,本篇我们实现一下用户协议。 1 创建页面 功能是点击用户协议的时候打开具体的协议内容,需要先创建一个页面。打开自定义应用&#x…...
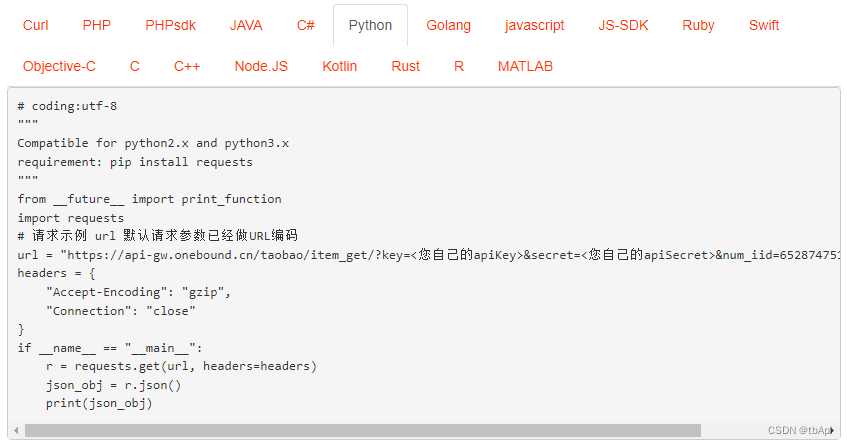
淘宝app商品详情源数据API接口(解决滑块问题)可高并发采集
通过API接口采集淘宝商品列表和app商品详情遇到滑块验证码的解决方法(带SKU和商品描述,支持高并发),主要是解决了高频情况下的阿里系滑块和必须要N多小号才能解决的反扒问题,以后都可以使用本方法: 大家都…...
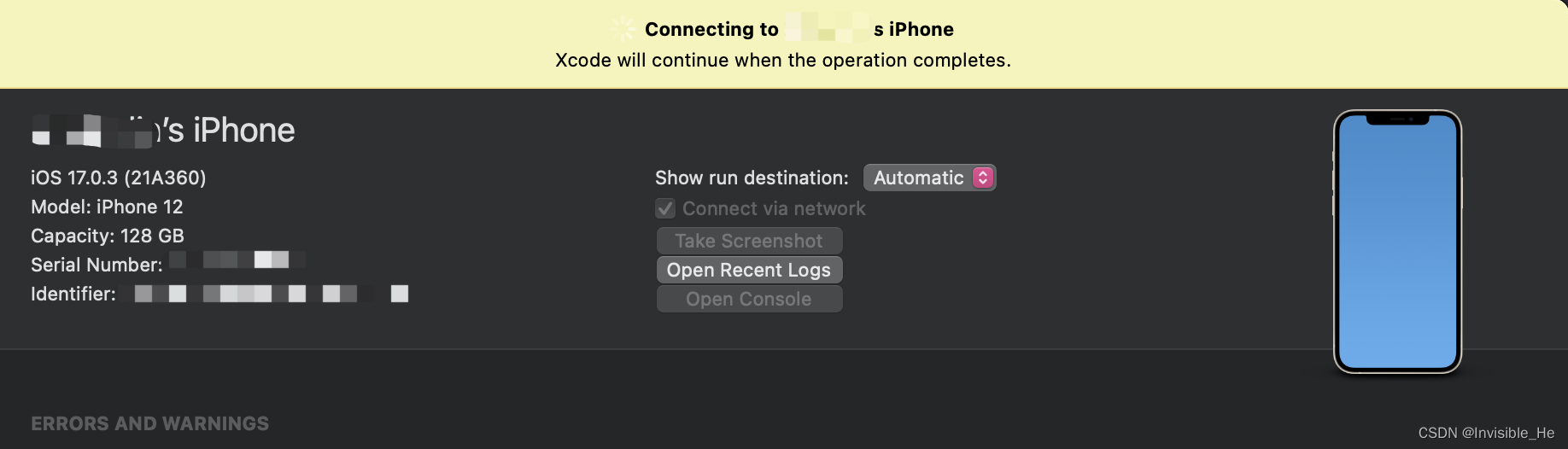
xcode15一直显示正在连接iOS17真机问题解决
前言 更新xcode15之后,出现了各种报错问题,可谓是一路打怪啊,解决一个报错问题又来一个。没想到到了最后还能出现一个一直显示正在连接iOS17真机的问题 一直显示正在连接iOS17真机的问题 问题截图如下: 解决方法 1. 打开De…...

stm32通过AT指令与esp8622通信
stm32通过AT指令与esp8622通信 文章目录 stm32通过AT指令与esp8622通信1.tcp通信2.mqtt通信 1.tcp通信 ATCWMODE1 设置为STA模式ATCWJAP_DEF"langtaotech","langtaotechXXX"ATCIPSTA? 查询ipATCIPMUX0 设置单连接ATCIPSTART"TCP","19…...

Flutter 类似onResume 监听,解决入场动画卡顿
在Flutter 实际开发过程中,页面数据往往是异步加载,接口请求回来后,数据刷新显示到界面上。 由于Flutter性能原因,也可能因为获取数据量比较大,在新页面路由进场动画执行过程中,接口请求结果回来了&#x…...
1024勋章
🌸关于重阳节的一些发疯日常(昨天的聊天记录,今天发系列)😅 🌸没错,发出来单纯觉得好玩儿😉(为了1024勋章😏)芜湖!...
C++栈、队列、优先级队列模拟+仿函数
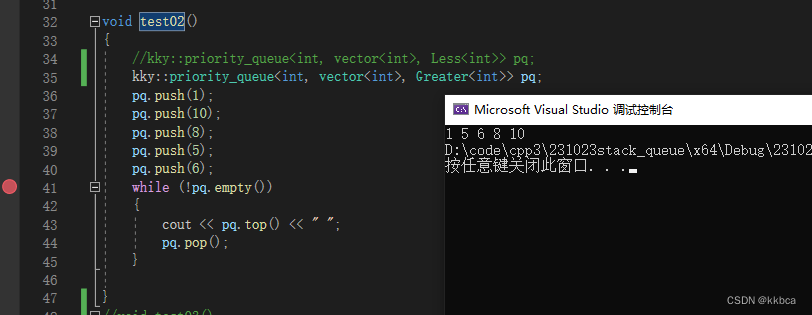
目录 一、栈的模拟和deque容器 1.deque 1.1deque结构 1.2deque优缺点 2.stack模拟 二、队列的模拟 三、priority_queue优先级队列 1.优先级队列模拟 2.添加仿函数 一、栈的模拟和deque容器 在之前,我们学过了C语言版本的栈,可以看这篇文章 栈和…...
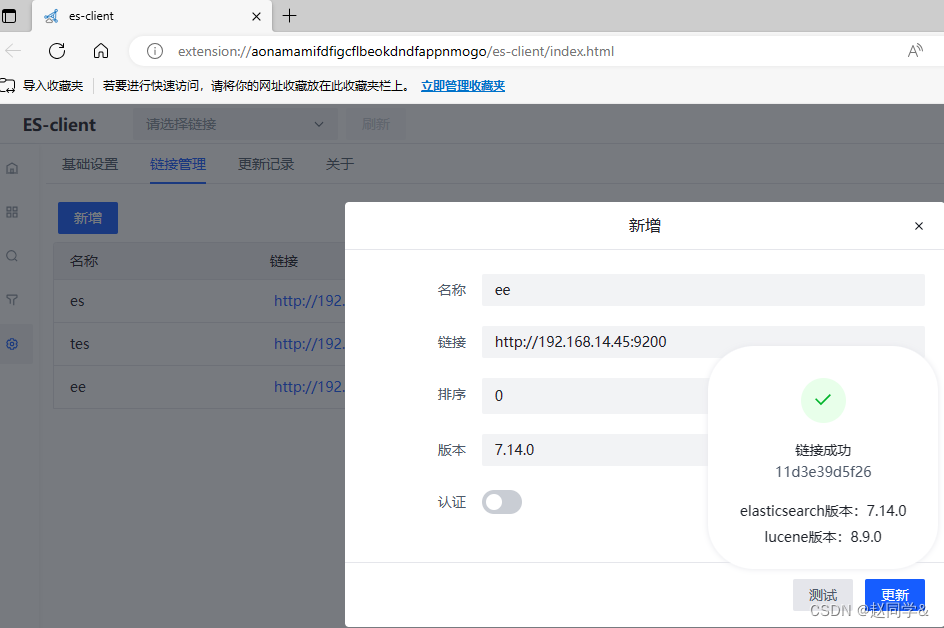
ES挂载不上怎么处理?
全文搜索 EelasticSearch安装 Docker安装 docker run -d --name es7 -e ES_JAVA_POTS"-Xms256m -Xmx256m" -e "discovery.typesingle-node" -v /home/206/es7/data/:/usr/share/elasticsearch/data -p 9200:9200 -p 9300:9300 elasticsearch:7.14.0 …...

问题与分类
设计问题 是否已经有类似的解决方案,是否需要当前的设计设计思路的文档话,背景-》 设计思路-》 好处与不足 -》 其他设计思路的对比(淘汰其他设计思路的原因) 设计思路的评审,如何评审,如何量化ÿ…...

021-Qt 配置GitHub Copilot
Qt 配置GitHub Copilot 文章目录 Qt 配置GitHub Copilot项目介绍 GitHub Copilot配置 GitHub CopilotQt 前置条件升级QtGitHub Copilot 前置条件激活的了GitHub Copilot账号安装 Neovim 启用插件,重启Qt配置 GitHub Copilo安装Nodejs下载[copilot.vim](https://gith…...

如何使用 PostgreSQL 进行数据迁移和整合?
PostgreSQL 是一个强大的开源关系型数据库管理系统,它提供了丰富的功能和灵活性,使其成为许多企业和开发者的首选数据库之一。在开发过程中,经常会遇到需要将数据从一个数据库迁移到另一个数据库,或者整合多个数据源的情况。…...

Qt Signals Slots VS QEvents - Qt跨线程异步操作性能测试与选取建议
相关代码参考:https://gitcode.net/coloreaglestdio/qtcpp_demo/-/tree/master/qt_event_signal 1.问题的由来 在对 taskBus 进行低延迟改造时,避免滥用信号与槽起到了较好的作用。笔者在前一篇文章中,叙述了通过避免广播式地播发信号&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
