【数据结构】常见复杂度习题详解 ------ 习题篇
文章目录
- 📋前言
- 一. ⛳️前篇回顾
- 二. ⛳️常见时间复杂度计算举例
- 1️⃣实例一
- 2️⃣实例二
- 3️⃣实例三
- 4️⃣实例四
- 5️⃣实例五
- 6️⃣实例六
- 7️⃣实例七
- 8️⃣实例八
- 三. ⛳️常见空间复杂度计算举例
- 1️⃣实例一
- 2️⃣实例二
- 3️⃣实例三
- 四. ⛳️总结
📋前言
🏠 个人主页:@聆风吟的个人主页
🔥系列专栏:本期文章收录在《数据结构初阶》,大家有兴趣可以浏览和关注,后面将会有更多精彩内容!
⏰寄语:少年有梦不应止于心动,更要付诸行动。
🎉欢迎大家关注🔍点赞👍收藏⭐️留言📝
🌈作者留言:本文从上篇文章《算法、时间复杂度和空间复杂度详解 》中剥离出来的,由于详解和题目放在一起篇幅过长,不利于大家更好吸收知识点,特此将其剥离出来。
一. ⛳️前篇回顾
上篇文章我们主要学习了:
- 算法的定义:算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
- 算法的特性:有穷性、确定性、可行性、输入、输出。
- 算法的设计要求:正确性、可读性、健壮性、高效率和低存储量需求。
- 算法的度量方法:事后统计方法、事前分析估算方法。
- 推导大O阶
- 时间复杂度
- 空间复杂度
你对以上的内容是否还能够全部回忆起来呢?如果你对某部分还有欠缺,请跳转该篇文章《算法、时间复杂度和空间复杂度详解 》进行复习,再配合着下面习题对时间复杂度和空间复杂度进行巩固。预计明天将会更新数据结构新文,大家抓紧时间在复习下前面知识。
二. ⛳️常见时间复杂度计算举例
1️⃣实例一
// 计算Func1的时间复杂度?
void Func1(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
解析:实例1基本操作执行了2N+10次,根据大O阶的推导方法很容易得出:Func1的时间复杂度为O(N)。
2️⃣实例二
// 计算Func2的时间复杂度?
void Func2(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
解析:实例二基本操作执行了M+N次,根据大O阶的推导方法得出:
- 如果题目没有表明 M 和 N 的大小,Func2的时间复杂度为
O(M + N); - 如果题目明确表明 M 远大于 N ,则 N 的变化对时间复杂度的影响不大,Func2的时间复杂度为
O(M); - 如果题目明确表明 N 远大于 M ,则 M 的变化对时间复杂度的影响不大,Func2的时间复杂度为
O(N)。 - 如果题目明确表明 M 和 N 一样大,则O(M + N)等价于O(2M)或O(2N),Func2的时间复杂度为
O(M)或O(N);
3️⃣实例三
// 计算Func3的时间复杂度?
void Func3(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
解析:实例3基本操作执行了100次,根据大O阶的推导方法很容易得出:Func3的时间复杂度为O(1)。
4️⃣实例四
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );
解析:首先我们先来介绍一下库函数strchr作用:在str指向的字符数组中查找是否包含字符characte。因此实例4的基本操作执行最好1次,最坏N次。根据时间复杂度一般看最坏,strchr的时间复杂度为O(N)。
5️⃣实例五
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
解析:本题是冒泡排序函数,冒泡排序的思想是:假设数组中有 n 个元素,第一趟执行将会执行 n-1 次交换,将一个元素排好序。第二趟将会执行 n-2 次交换,将将一个元素排好序…依次类推。排好所有元素需要执行 n-1 次,每趟交换的次数分别为(n - 1),(n-2),(n-3),… ,(2),(1)。由此可知,实例5基本操作执行最好n-1次(即数组已经排好序,只需要执行一趟排序判断数组是否已经有序),最坏执行了( n*(n-1) )/2次(即将所有趟交换的次数相加,可以直接使用等差数列求和),通过推导大O阶方法+时间复杂度一般看最坏,BubbleSort的时间复杂度为O(N^2)。
6️⃣实例六
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
解析:本题是二分查找函数,每次查找将会将范围缩放一半。因此实例6基本操作执行最好1次,最坏O(logN)次。根据时间复杂度一般看最坏,BinarySearch时间复杂度为 O(logN) 。

7️⃣实例七
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
解析:本题是一个简单的递归调用, 实例7通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。

8️⃣实例八
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
解析:本题是一个双递归。实例8通过计算分析发现基本操作递归了2n,Fib的时间复杂度为O(2^n)。

三. ⛳️常见空间复杂度计算举例
1️⃣实例一
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
解析: 实例1使用了常数个额外空间,分别是[ end,exchange,i ]。根据大O阶的推导方法很容易得出,BubbleSort空间复杂度为 O(1)
2️⃣实例二
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}
解析:实例2动态开辟了N+1个空间,根据大O阶的推导方法很容易得出,Fibonacci空间复杂度为 O(N)。
3️⃣实例三
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
解析:实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)。

四. ⛳️总结
本文通过大量实例讲解常见时间复杂和空间复杂度计算,希望通过这些例子的讲解能够帮助你在以后的学习中能够更加灵活、精确的计算出一个程序的复杂度,方便我们更快的寻找解决一个问题的最优的算法。
今天的内容就到这里了,你对今天的内容是否有所掌握?如果还有疑问的话请在评论区里多多提问,大家可以一起帮你解决,让我们共同进步。创作不易,如果对你有用的的话点个赞支持下作者,你们的支持是作者创作最大的动力。关注我不迷路,让我们下期不见不散✋✋。
相关文章:

【数据结构】常见复杂度习题详解 ------ 习题篇
文章目录 📋前言一. ⛳️前篇回顾二. ⛳️常见时间复杂度计算举例1️⃣实例一2️⃣实例二3️⃣实例三4️⃣实例四5️⃣实例五6️⃣实例六7️⃣实例七8️⃣实例八 三. ⛳️常见空间复杂度计算举例1️⃣实例一2️⃣实例二3️⃣实例三 四. ⛳️总结 📋前言 …...

一、vue介绍
一、介绍 vue式前端框架,是一套用于构建用户界面的渐进式框架 1、安装vue 安装node.js(配置环境变量) https://nodejs.org/en/download/ 更换镜像 npm config set registry https://registry.npm.taobao.org 查看镜像 npm config get regi…...

Linux ARMv8 异常向量表
http://blog.chinaunix.net/uid-69947851-id-5830546.html 本章接着《Linux内核启动》部分讲解,我们知道了在进入start_kernel之前,通过指令adr_l x8, vectors;msr vbar_el1, x8设置了异常向量表,那么异常向量表的结构是怎么样…...

C++基类和派生类的内存分配,多态的实现
目录 基类和派生类的内存分配基类和派生类的成员归属多态的实现 基类和派生类的内存分配 类包括成员变量(data member)和成员函数(member function)。 成员变量分为静态数据(static data)和非静态数据&…...

C/C++基础
C 二进制 问题:二进制怎么表示整数、小数、正数、负数,如何存储?加减乘除怎么运算(见文章《计算机加减乘除本质》)? 变量 c定义一个变量的时候,需要事先定义变量大小和变量类型。 //有符号…...
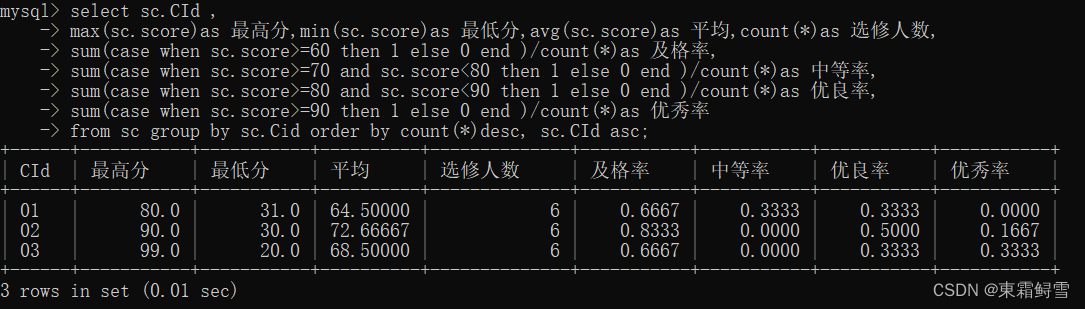
MySQL基础练习题
数据表介绍 --1.学生表 Student(SId,Sname,Sage,Ssex) --SId 学生编号,Sname 学生姓名,Sage 出生年月,Ssex 学生性别 --2.课程表 Course(CId,Cname,TId) --CId 课程编号,Cname 课程名称,TId 教师编号 --3.教师表 Teacher(TId,Tname) --TId 教师编号,Tname 教师姓名 --4.成绩…...

【C语言学习笔记 --- 动态内存管理】
C语言程序设计笔记---029 C语言之动态内存管理1、介绍动态内存管理2、动态内存函数的介绍2.1、malloc和free函数2.2、calloc函数2.3、realloc函数 3、动态内存管理过程中,一些常见的错误3.1、对NULL指针的解引用操作3.2、对动态内存开辟的空间的越界访问3.3、对非动…...

Nougat来了,能否成为pdf格式转换的新神器?
Nougat来了,能否成为pdf格式转换的新神器? 论文链接:https://arxiv.org/pdf/2308.13418v1.pdf 项目地址:https://github.com/facebookresearch/nougat What happened?🤨 科学知识主要存储在书籍和科学期…...
C++文件和流
到目前为止,我们已经使用了 iostream 标准库,它提供了 cin 和 cout 方法分别用于从标准输入读取流和向标准输出写入流。 本教程介绍如何从文件读取流和向文件写入流。这就需要用到 C 中另一个标准库 fstream,它定义了三个新的数据类型&#x…...

代码随想录算法训练营第23期day31|贪心算法理论基础、455.分发饼干、376. 摆动序列、53. 最大子序和
目录 一、贪心算法理论基础 二、(leetcode 455)分发饼干 三、(leetcode 376)摆动序列 四、(leetcode 53)最大子序和 一、贪心算法理论基础 1.什么是贪心 贪心的本质是选择每一阶段的局部最优…...

mdadm命令详解及实验过程
mdadm命令详解及实验过程 ⼀.概念 mdadm是multiple devices admin的简称,它是Linux下的⼀款标准的软件 RAID 管理⼯具,作者是Neil Brown ⼆.特点 mdadm能够诊断、监控和收集详细的阵列信息 mdadm是⼀个单独集成化的程序⽽不是⼀些分散程序的集合&#…...

推荐几个程序员必逛的个人技术博客网站
1、美团技术团队 地 址: 美团技术团队简 介:美团技术团队的博客,干货满满。推荐指数:⭐⭐⭐⭐⭐ 2、阮一峰的网络日志 地 址: 阮一峰的个人网站 - Ruan YiFengs Personal Website简 介:大神阮一峰,博客风格真正…...
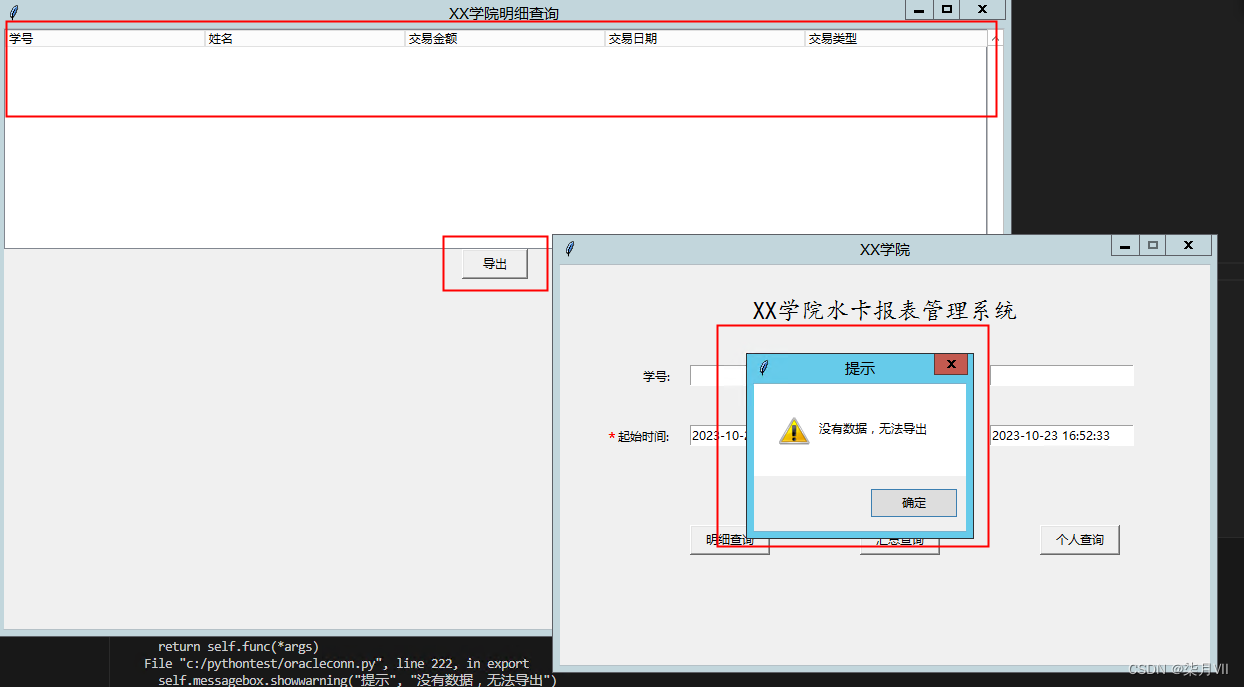
Python桌面应用之XX学院水卡报表查询系统(Tkinter+cx_Oracle)
一、功能样式 Python桌面应用之XX学院水卡报表查询系统功能: 连接Oracle数据库,查询XX学院水卡操作总明细报表,汇总数据报表,个人明细报表,进行预览并且支持导出报表 1.总明细报表样式 2.汇总明细样式 3.个人明细…...
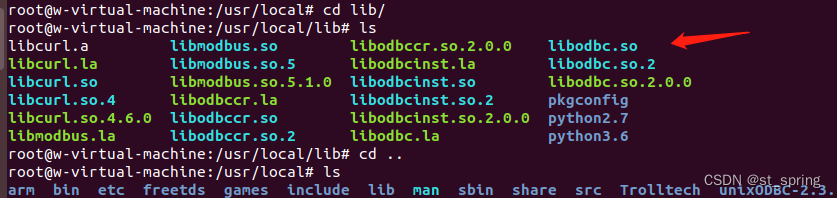
ubuntu 中使用Qt连接MMSQl,报错libqsqlodbc.so: undefined symbol: SQLAllocHandle
Qt4.8.7的源码编译出来的libqsqlodbc.so,在使用时报错libqsqlodbc.so: undefined symbol: SQLAllocHandle,需要在编译libqsqlodbc.so 的项目pro文件加上LIBS -L/usr/local/lib -lodbc。 这里的路径根据自己的实际情况填写。 编辑: 使用uni…...

笔试,猴子吃香蕉,多线程写法
package demo;import java.util.concurrent.CountDownLatch;/*** description: 猴子吃香蕉* author: wxm* create: 2023-10-23 14:01**/ public class Main {public static void main(String[] args) throws InterruptedException {Monkey[] m new Monkey[3];Resource r new …...
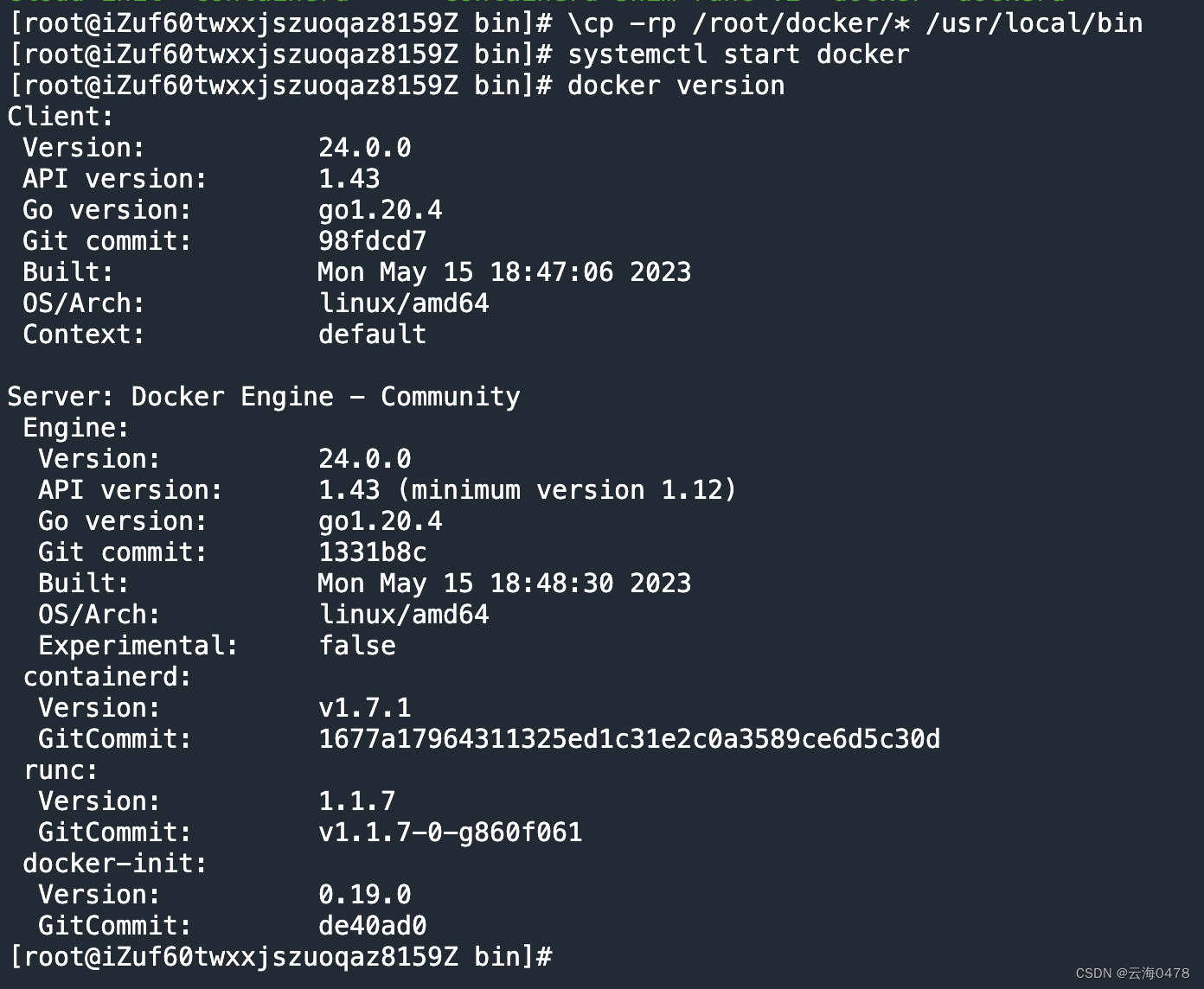
安装docker ,更换docker版本
docker dockerd & containerd Dockerd(Docker 守护进程)在其底层使用 Containerd 来管理容器。Containerd 是一个开源的容器运行时管理器,由 Docker 公司于2017年开发并开源,它负责实际的容器生命周期管理。 以下是 Docker 守…...
英语小作文写作模板及步骤(1)
...

编写hello驱动程序
hello的驱动编写 编写驱动程序的步骤 1.确定主设备号,也可以让内核分配 2.定义自己的 file_operations 结构体 3.实现对应的 drv_open/drv_read/drv_write 等函数,填入 file_operations 结构 体 4.把 file_operations 结构体告诉内核:regist…...

ZYNQ中断例程
GPIO 中断系统初始化流程: 第一步:初始化 cpu 的异常处理功能 第二步:初始化中断控制器 第三步:向 CPU 注册异常处理回调函数; 第四步:将中断控制器中的对应中断 ID 的中断与中断控制器相连接 第五步:设置 …...
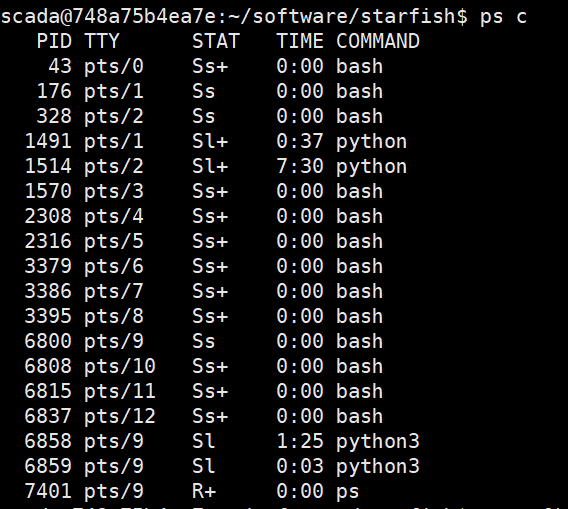
常用linux命令 linux_cmd_sheet
查看文件大小 ls -al 显示每个文件的kb大小 查看系统日志 dmesg -T | tail 在 top 命令中,RES 和 VIRT(或者 total-vm)是用来表示进程内存使用的两个不同指标,它们之间有以下区别: RES(Resident Set Size…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
