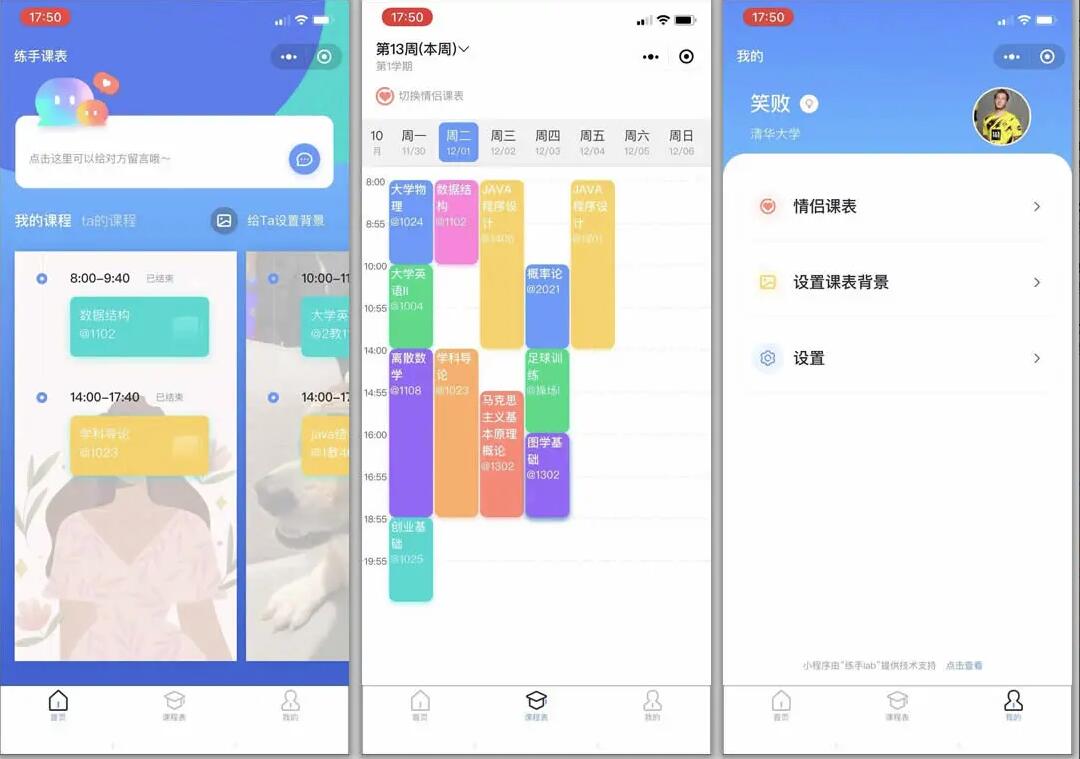
支持多校 微信课表小程序源码 排课小程序源码 支持导入课表 情侣课表 背景设置
练手Lab课程表小程序源码是一个基于thinkphp系统进行开发的前后端分离系统。
源码功能介绍
1、情侣功能
2、情侣间留言
3、情侣间互相设置课程表背景
4、自己日、周课程表背景设置
5、教务系统课程表导入
6、导入别人分享的课表
7、导入别人分享的单课
8、多校支持
9、首页顶部氛围设置(管理员设置,节日氛围)
环境要求
1、服务端:php+mysql(基于FastAdmin)
2、小程序端:原生+colorui
准备工作
1、需自备服务器和备案过的域名
2、申请https证书,dnspod网站可以免费申请一年的
3、安装PHP运行环境(PHP >= 7.1 且 = 5.5.0)
4、到微信公众平台,申请一个小程序,获取AppID和AppSecret
服务端部署教程
1、添加站点并上传代码至根目录
2、绑定到项目中的public目录为运行目录,伪静态选择thinkphp
3、输入你绑定的域名,会自动跳转至安装界面
4、根据提示安装(以上三步其实是安装FastAdmin框架)
5、进入后台,插件管理里面,搜索“练手课表”,安装
6、安装第三方登录插件
7、设置小程序AppID和AppSecret(微信公众平台获取),练手Lab秘钥(独立版部署的话,自己生成一个16位的字符串就行),站点id不要改!!!
8、服务端部署完毕
小程序端部署教程
小程序端源码在wxapp文件夹下
在微信开发者工具里面,左上角选择项目,导入项目,选择这个文件夹
1、修改config.js文件下的cryptoKey,自己生成一个16位的字符串
2、修改baseUrl里面的域名,改成你自己的(注意在微信公众平台里面,添加白名单)
3、修改project.config.json文件里面的appid为自己的
4、微信开发者工具,右上角详情里面,勾选ES6转ES5
5、如果报错,请检查是否配置了白名单,配置之后,在项目配置里面(见上图右上角),点刷新
6、预览,没问题就可以上传了
使用手册
1、首页顶部氛围设置。因为课程表小程序太工具了,没有杂七杂八的功能,所以可运营空间不强,所以增加了这个功能,如端午,中秋换个背景之类的,甚至可以开放投稿,让学生拍校园风景并给其署名,每日更换一张。
2、可以分学校设置上课时间、冬、夏令时日期,互相之间不影响,到日期自动切换
3、导入教务系统课程表需要适配,目前支持正方和青果的教务系统
4、分享整个课程表,可以生成小程序码,适用于同一个班级,课程表一致的情况,直接打印小程序码让同学扫就可以导入课程表
5、分享单课,适用于每个同学的课程表都不一致的情况,可以直接在教室门口贴单课的小程序码,只导入该课的课表
源码下载:https://download.csdn.net/download/m0_66047725/88425824
源码下载2:关注我留言
相关文章:

支持多校 微信课表小程序源码 排课小程序源码 支持导入课表 情侣课表 背景设置
练手Lab课程表小程序源码是一个基于thinkphp系统进行开发的前后端分离系统。 源码功能介绍 1、情侣功能 2、情侣间留言 3、情侣间互相设置课程表背景 4、自己日、周课程表背景设置 5、教务系统课程表导入 6、导入别人分享的课表 7、导入别人分享的单课 8、多校支持 9…...
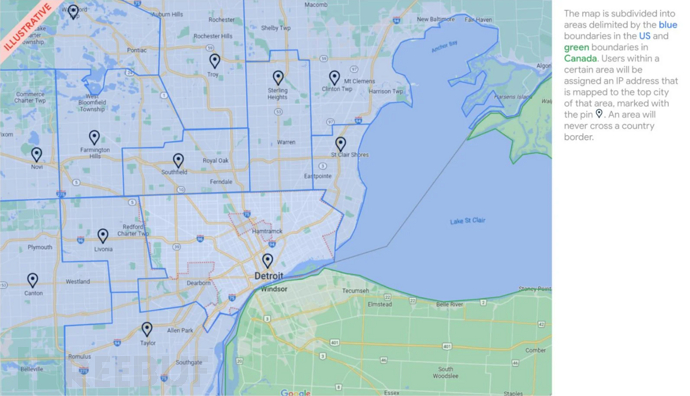
谷歌计划从Chrome119起测试IP隐私保护功能
目前,谷歌正为Chrome浏览器测试一项新的“IP保护”功能。因为该公司认为用户IP地址一旦被黑客滥用或秘密跟踪,都可能导致用户隐私信息泄露。 而这项功能可通过代理服务器屏蔽用户的IP地址,以增强用户的隐私性,这样就可以尽量在确…...
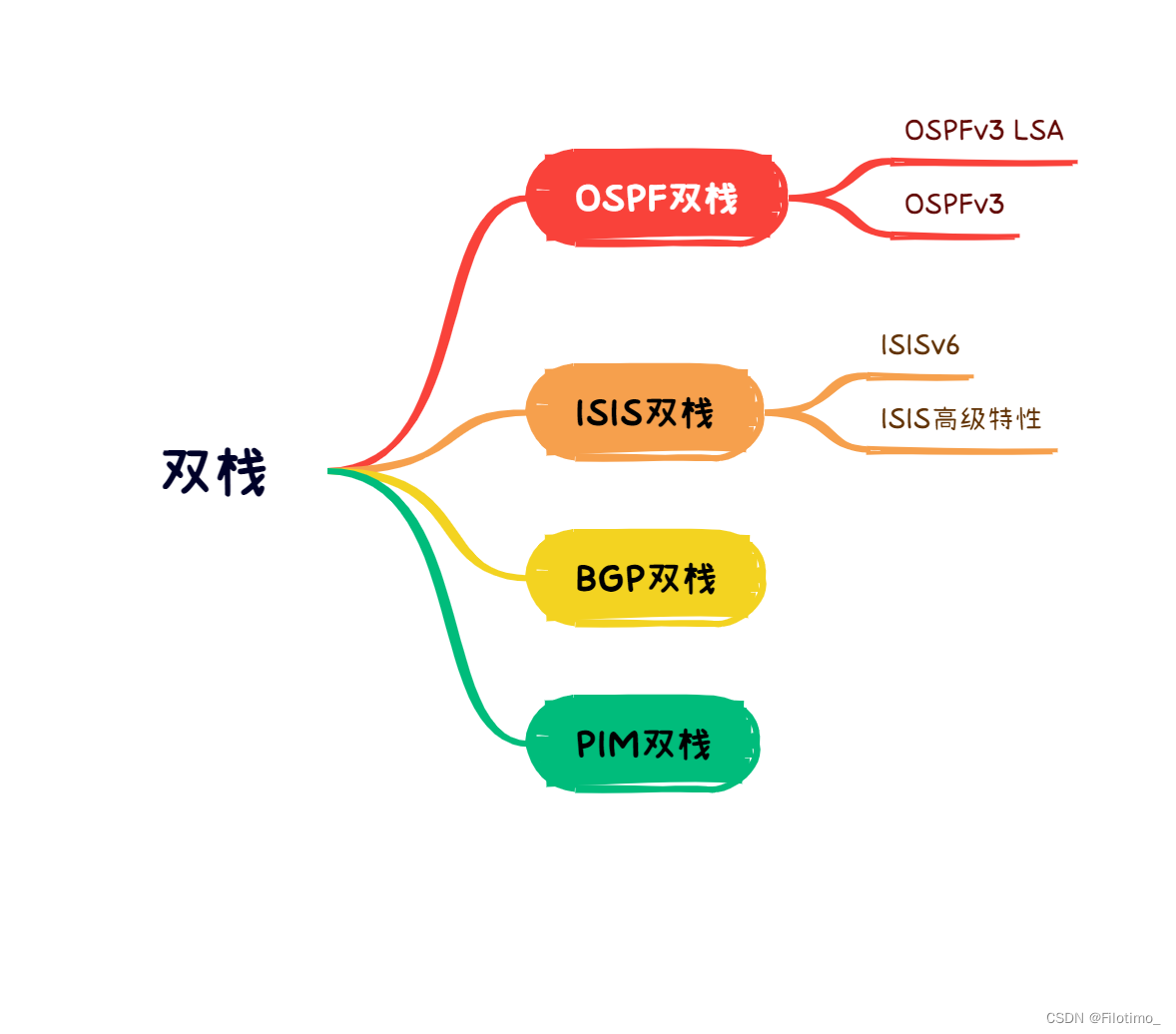
【技能树笔记】网络篇——练习题解析(九)
目录 前言 一、OSPF双栈 1.1 OSPFv3 LSA 1.2 OSPFv3 二、ISIS双栈 2.1 ISISv6 2.2 ISIS高级特性 三、BGP双栈 四、PIM双栈 总结 🌈嗨!我是Filotimo__🌈。很高兴与大家相识,希望我的博客能对你有所帮助。 💡本文由Filot…...
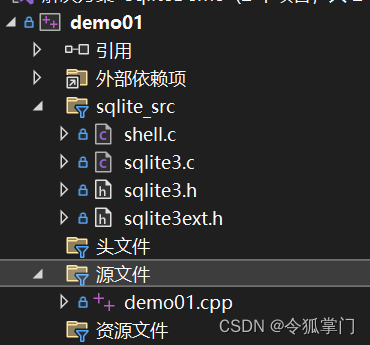
c++ qt连接操作sqlite
qt客户端编程,用到数据库的场景不多,但是部分项目还是需要数据库来保存同步数据,客户端用到的数据库,一般是sqlite。 Qt提供了数据库模块,但是qt本身的数据库模块并不好用,会有各种问题, 建议大家不要,可以自己封装数据库的操作。本篇博客介绍qt连接操作sqlite。 sqlit…...
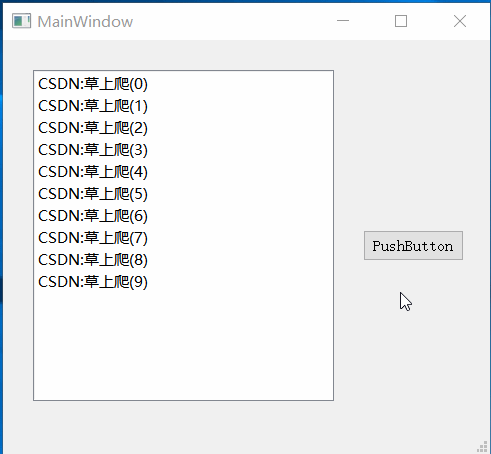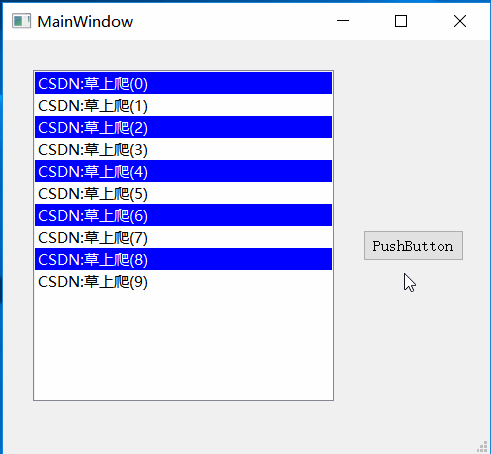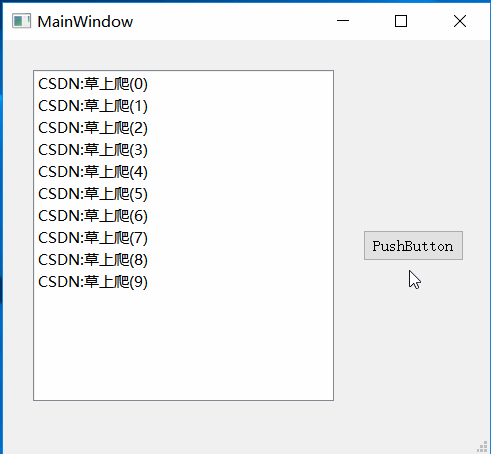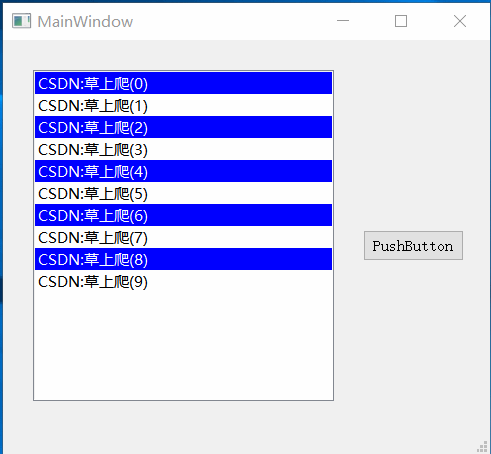
Qt之自定义QStringListModel设置背景色和前景色
一.效果 二.实现 QStringListModel里只实现了Qt::EditRole和Qt::DisplayRole,不能直接设置背景色和前景色,所以我们要继承QStringListModel,重写其中的data和setData方法,使其支持Qt::ForegroundRole和Qt::BackgroundRole。 QHStringListModel.h #ifndef QHSTRINGLISTMO…...
人工智能基础_机器学习001_线性回归_多元线性回归_最优解_基本概念_有监督机器学习_jupyter notebook---人工智能工作笔记0040
线性和回归,就是自然规律,比如人类是身高趋于某个值的概率最大,回归就是通过数学方法找到事物的规律. 机器学习作用: 该专业实际应用于机器视觉、指纹识别、人脸识别、视网膜识别、虹膜识别、掌纹识别、专家系统、自动规划、智能搜索、定理证明、博弈、自动程序设计、智能控制…...
)
Linux 错误处理(字符设备基础三)
在Linux字符设备驱动中,即使是最简单的注册字符设备,也存在注册失败的可能性,因此在之前编写的驱动代码中采用检查函数返回值的方式,确认函数是否成功执行 一、goto 语句 在编写驱动程序时,驱动程序应该提供函数执行失…...

STM32 PWM配置及呼吸灯
PWM的英文全称是"Pulse Width Modulation",中文翻译为"脉冲宽度调制"。 在PWM中可以调节的其实只有两个东西,一个叫做可调周期(调频率),另一个叫做占空比(高电平/周期)。 而…...

华为云 CodeArts Snap 智能编程助手 PyCharm 插件安装与使用指南
1 插件安装下载 1.1 搜索插件 打开 PyCharm,选择 File,点击 Settings。 选择 Plugins,点击 Marketplace,并在搜索框中输入 Huawei Cloud CodeArts Snap。 1.2 安装插件 如上图所示,点击 Install 按钮安装 Huawei Cl…...
SpringSecurity分布式安全框架
Spring Security是一个基于Spring框架的安全框架,它提供了全面的安全解决方案,包括用户认证和用户授权等Web应用安全性问题。Spring Security可以轻松扩展以满足自定义需求,它的真正强大之处在于它可以轻松扩展以满足自定义要求。 对于分布式…...

高速下载b站视频的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

Qt之彻底解决QSpinBox限定范围无效的问题
QSpinBox有个比较啃爹的问题,不管取值范围设置为多少,都能一直输入0,如下图所示: 当取值范围包含负数时,负号后也可以一直输入0,如下图所示: 还有就是当取值范围设置为10以上时,比如10~100,却可以输入1~9 虽然上述非法输入最终都未生效,当QSpinBox失去焦点时会显示为…...

Ktor vs Spring Boot:哪个框架能帮助你构建更高性能的 Web 应用?
文章首发地址 Ktor 和 Spring Boot 是两个在 Kotlin Web 开发中常用的框架,它们有一些共同点,也有一些区别。 共同点: 都支持 Kotlin:Ktor 和 Spring Boot 都能够完全支持 Kotlin 语言,这使得开发者可以使用 Kotlin …...
【Ubuntu18.04】激光雷达与相机联合标定(Livox+HIKROBOT)(一)
LivoxHIKROBOT联合标定 引言1 海康机器人HIKROBOT SDK二次开发并封装ROS1.1 介绍1.2 安装MVS SDK1.3 封装ROS packge 2 览沃Livox SDK二次开发并封装ROS3 相机雷达联合标定3.1 环境配置3.1.1 安装依赖——PCL 安装3.1.2 安装依赖——Eigen 安装3.1.3 安装依赖——Ceres-solver …...
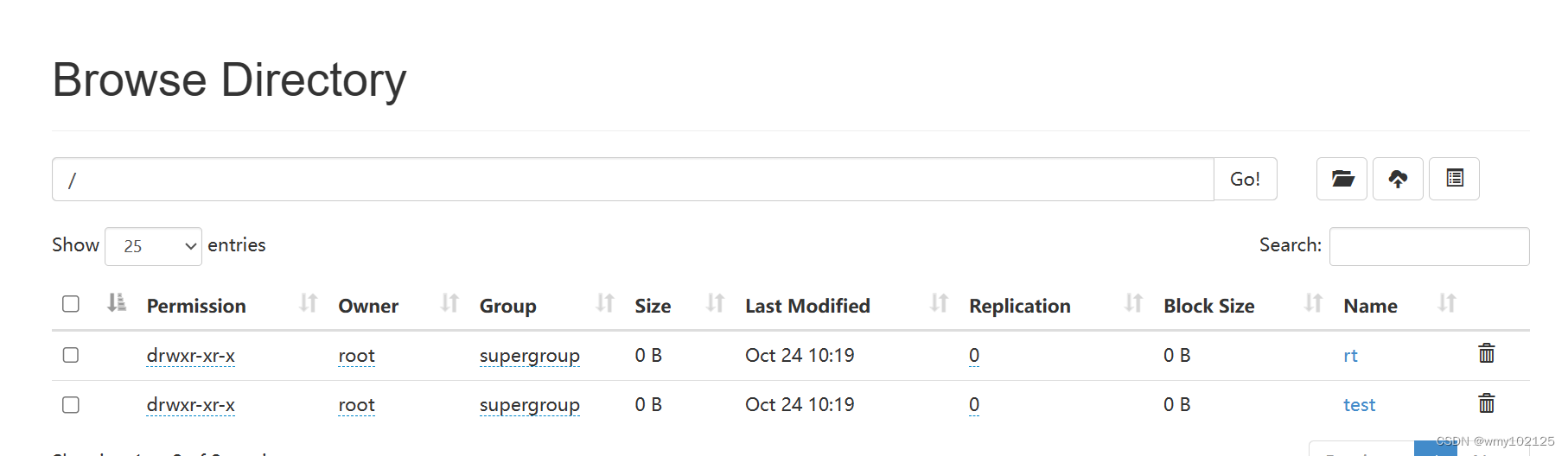
hadoop伪分布式安装部署
首先jdk安装完毕 jdk安装文档参考: Linux 环境下安装JDK1.8并配置环境变量_linux安装jdk1.8并配置环境变量_Xi-Yuan的博客-CSDN博客 准备好hadoop的安装包 我的下载地址如下: We Transfer Gratuit. Envoi scuris de gros fichiers. 将hadoop包上传到随…...

前端视角看 Docker : 加速开发和部署的利器
Docker 是一个开源的容器化平台,大大的降低了运维相关的工作。在日常开发中,中小公司很少有专职运维,所以在开发中通过使用 Docker,前端相关工作可以更加高效地构建、打包、部署和运行应用程序。此系列将从前端的视角出发…...

JVM相关的面试题
一、什么是程序计数器 二、简要的介绍一下堆 三、什么是虚拟机栈 四、能不能解释下方法区 五、你听过直接内存吗? 六、什么是类加载器,类加载器有哪些 七、什么是双亲委派模型 八、JVM为什么采用双亲委派机制 九、类装载的执行过程 十、对象什么时候被垃…...

HTML、CSS和jQuery:实现图片折叠展开的效果
在网页设计和开发中,我们经常需要实现一些动态特效来增加页面的吸引力和交互性。其中,图片折叠展开特效是一种常见但又很有趣的技巧。通过这种特效,我们可以让图片在用户的操作下折叠或展开,从而展示更多的内容或细节。以下介绍如…...

php简单后门实现及php连接数据库
php简单后门实现 代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>easybackdoor</title>…...

IOS课程笔记[6] 基础控件
UILabel 控件 frame 设置尺寸 [lb setFrame:CGRectMake(5, 0, 400, 40)];Font 字体设置 [lb setFont:[UIFont systemFontOfSize:20.f]] [lb setFont:[UIFont boldSystemFontOfSize:25.f]]; [lb setFont:[UIFont italicSystemFontOfSize:23.f]];背景色 [lb setBackgroundC…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
