《动手学深度学习 Pytorch版》 10.2 注意力汇聚:Nadaraya-Watson 核回归
import torch
from torch import nn
from d2l import torch as d2l
1964 年提出的 Nadaraya-Watson 核回归模型是一个简单但完整的例子,可以用于演示具有注意力机制的机器学习。
10.2.1 生成数据集
根据下面的非线性函数生成一个人工数据集,其中噪声项 ϵ \epsilon ϵ 服从均值为 0 ,标准差为 0.5 的正态分布:
y i = 2 sin x i + x i 0.8 + ϵ \boldsymbol{y}_i=2\sin{\boldsymbol{x}_i}+\boldsymbol{x}_i^{0.8}+\epsilon yi=2sinxi+xi0.8+ϵ
n_train = 50 # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5) # 排序后的训练样本def f(x):return 2 * torch.sin(x) + x**0.8y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,)) # 训练样本的输出
x_test = torch.arange(0, 5, 0.1) # 测试样本
y_truth = f(x_test) # 测试样本的真实输出
n_test = len(x_test) # 测试样本数
n_test
50
def plot_kernel_reg(y_hat): # 绘制训练样本d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])d2l.plt.plot(x_train, y_train, 'o', alpha=0.5);
10.2.2 平均汇聚
先使用最简单的估计器来解决回归问题。基于平均汇聚来计算所有训练样本输出值的平均值:
f ( x ) = 1 n ∑ i = 1 n y i f(x)=\frac{1}{n}\sum^n_{i=1}y_i f(x)=n1i=1∑nyi
y_hat = torch.repeat_interleave(y_train.mean(), n_test) # 计算平均并进行扩展
plot_kernel_reg(y_hat)

10.2.3 非参数注意力汇聚
相对于平均汇聚的忽略输入。Nadaraya 和 Watson 提出了一个更好的想法,根据输入的位置对输出 y i y_i yi 进行加权,即 Nadaraya-Watson 核回归:
f ( x ) = ∑ i = 1 n K ( x − x i ) ∑ j = 1 n K ( x − x j ) y i f(x)=\sum^n_{i=1}\frac{K(x-x_i)}{\sum^n_{j=1}K(x-x_j)}y_i f(x)=i=1∑n∑j=1nK(x−xj)K(x−xi)yi
将其中的核(kernel) K K K 根据上节内容重写为更通用的注意力汇聚公式:
f ( x ) = ∑ i = 1 n α ( x , x i ) y i f(x)=\sum^n_{i=1}\alpha(x,x_i)y_i f(x)=i=1∑nα(x,xi)yi
参数字典:
-
x x x 为查询
-
( x i , y i ) (x_i,y_i) (xi,yi) 为键值对
-
α ( x , x i ) \alpha(x,x_i) α(x,xi) 为注意力权重(attention weight),即查询 x x x 和键 x i x_i xi 之间的关系建模,此权重被分配给对应值的 y i y_i yi。
对于任何查询,模型在所有键值对注意力权重都是一个有效的概率分布: 非负的且和为1。
考虑高斯核(Gaussian kernel)以更好地理解注意力汇聚:
K ( u ) = 1 2 π exp ( − u 2 2 ) K(u)=\frac{1}{\sqrt{2\pi}}\exp{(-\frac{u^2}{2})} K(u)=2π1exp(−2u2)
将高斯核代入上式可得:
f ( x ) = ∑ i = 1 n α ( x , x i ) y i = ∑ i = 1 n exp ( − 1 2 ( x − x i ) 2 ) ∑ j = 1 n exp ( − 1 2 ( x − x j ) 2 ) y i = ∑ i = 1 n s o f t m a x ( − 1 2 ( x − x i ) 2 ) y i \begin{align} f(x)=&\sum^n_{i=1}\alpha(x,x_i)y_i\\ =&\sum^n_{i=1}\frac{\exp{(-\frac{1}{2}(x-x_i)^2)}}{\sum^n_{j=1}\exp{(-\frac{1}{2}(x-x_j)^2)}}y_i\\ =&\sum^n_{i=1}\mathrm{softmax}\left(-\frac{1}{2}(x-x_i)^2\right)y_i \end{align} f(x)===i=1∑nα(x,xi)yii=1∑n∑j=1nexp(−21(x−xj)2)exp(−21(x−xi)2)yii=1∑nsoftmax(−21(x−xi)2)yi
如果一个键 x i x_i xi 越是接近给定的查询 x x x,那么分配给这个键对应值 y i y_i yi 的注意力权重就会越大,也就“获得了更多的注意力”。
上式是一个非参数的注意力汇聚(nonparametric attention pooling)模型。 接下来基于这个非参数的注意力汇聚模型绘制的预测结果的模型预测线是平滑的,并且比平均汇聚的预测更接近真实。
# X_repeat的形状:(n_test,n_train),
# 每一行都包含着相同的测试输入(例如:同样的查询)
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))
# x_train包含着键。attention_weights的形状:(n_test,n_train),
# 每一行都包含着要在给定的每个查询的值(y_train)之间分配的注意力权重
attention_weights = nn.functional.softmax(-(X_repeat - x_train)**2 / 2, dim=1)
# y_hat的每个元素都是值的加权平均值,其中的权重是注意力权重
y_hat = torch.matmul(attention_weights, y_train)
plot_kernel_reg(y_hat)

观察注意力的权重可以发现,“查询-键”对越接近,注意力汇聚的注意力权重就越高。
d2l.show_heatmaps(attention_weights.unsqueeze(0).unsqueeze(0),xlabel='Sorted training inputs',ylabel='Sorted testing inputs')

10.2.4 带参数的注意力汇聚
可以轻松地将可学习的参数集成到注意力汇聚中,例如,在下面的查询 x x x 和键 x i x_i xi 之间的距离乘以可学习参数 w w w:
f ( x ) = ∑ i = 1 n α ( x , x i ) y i = ∑ i = 1 n exp ( − 1 2 ( ( x − x i ) w ) 2 ) ∑ j = 1 n exp ( − 1 2 ( ( x − x j ) w ) 2 ) y i = ∑ i = 1 n s o f t m a x ( − 1 2 ( ( x − x i ) w ) 2 ) y i \begin{align} f(x)=&\sum^n_{i=1}\alpha(x,x_i)y_i\\ =&\sum^n_{i=1}\frac{\exp{(-\frac{1}{2}((x-x_i)w)^2)}}{\sum^n_{j=1}\exp{(-\frac{1}{2}((x-x_j)w)^2)}}y_i\\ =&\sum^n_{i=1}\mathrm{softmax}\left(-\frac{1}{2}((x-x_i)w)^2\right)y_i \end{align} f(x)===i=1∑nα(x,xi)yii=1∑n∑j=1nexp(−21((x−xj)w)2)exp(−21((x−xi)w)2)yii=1∑nsoftmax(−21((x−xi)w)2)yi
10.2.4.1 批量矩阵乘法
假定两个张量的形状分别是 ( n , a , b ) (n,a,b) (n,a,b) 和 ( n , b , c ) (n,b,c) (n,b,c),它们的批量矩阵乘法输出的形状为 ( n , a , c ) (n,a,c) (n,a,c)。
。
X = torch.ones((2, 1, 4))
Y = torch.ones((2, 4, 6))
torch.bmm(X, Y).shape
torch.Size([2, 1, 6])
可以使用小批量矩阵乘法来计算小批量数据中的加权平均值。
weights = torch.ones((2, 10)) * 0.1
values = torch.arange(20.0).reshape((2, 10))
weights.shape, values.shape, weights.unsqueeze(1).shape, values.unsqueeze(-1).shape, torch.bmm(weights.unsqueeze(1), values.unsqueeze(-1))
(torch.Size([2, 10]),torch.Size([2, 10]),torch.Size([2, 1, 10]),torch.Size([2, 10, 1]),tensor([[[ 4.5000]],[[14.5000]]]))
10.2.4.2 定义模型
class NWKernelRegression(nn.Module):def __init__(self, **kwargs):super().__init__(**kwargs)self.w = nn.Parameter(torch.rand((1,), requires_grad=True))def forward(self, queries, keys, values):# queries和attention_weights的形状为(查询个数,“键-值”对个数)queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))self.attention_weights = nn.functional.softmax(-((queries - keys) * self.w)**2 / 2, dim=1)# values的形状为(查询个数,“键-值”对个数)return torch.bmm(self.attention_weights.unsqueeze(1),values.unsqueeze(-1)).reshape(-1)
10.2.4.3 训练
# X_tile的形状:(n_train,n_train),每一行都包含着相同的训练输入
X_tile = x_train.repeat((n_train, 1))
# Y_tile的形状:(n_train,n_train),每一行都包含着相同的训练输出
Y_tile = y_train.repeat((n_train, 1))
# keys的形状:('n_train','n_train'-1)
keys = X_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
# values的形状:('n_train','n_train'-1)
values = Y_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
net = NWKernelRegression()
loss = nn.MSELoss(reduction='none') # 使用平方损失函数
trainer = torch.optim.SGD(net.parameters(), lr=0.5) # 使用随机梯度下降
animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])for epoch in range(5):trainer.zero_grad()l = loss(net(x_train, keys, values), y_train)l.sum().backward()trainer.step()print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')animator.add(epoch + 1, float(l.sum()))

训练完带参数的注意力汇聚模型后可以发现:在尝试拟合带噪声的训练数据时,预测结果绘制的线不如之前非参数模型的平滑。
# keys的形状:(n_test,n_train),每一行包含着相同的训练输入(例如,相同的键)
keys = x_train.repeat((n_test, 1))
# value的形状:(n_test,n_train)
values = y_train.repeat((n_test, 1))
y_hat = net(x_test, keys, values).unsqueeze(1).detach()
plot_kernel_reg(y_hat)

与非参数的注意力汇聚模型相比, 带参数的模型加入可学习的参数后, 曲线在注意力权重较大的区域变得更不平滑。
d2l.show_heatmaps(net.attention_weights.unsqueeze(0).unsqueeze(0),xlabel='Sorted training inputs',ylabel='Sorted testing inputs')

练习
(1)增加训练数据的样本数量,能否得到更好的非参数的 Nadaraya-Watson 核回归模型?
不能。
n_train_more = 500
x_train_more, _ = torch.sort(torch.rand(n_train_more) * 5)def f(x):return 2 * torch.sin(x) + x**0.8y_train_more = f(x_train_more) + torch.normal(0.0, 0.5, (n_train_more,))
x_test_more = torch.arange(0, 5, 0.01)
y_truth_more = f(x_test_more)def plot_kernel_regv_more(y_hat_more):d2l.plot(x_test_more, [y_truth_more, y_hat_more], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])d2l.plt.plot(x_train_more, y_train_more, 'o', alpha=0.5);X_repeat_more = x_test_more.repeat_interleave(n_train_more).reshape((-1, n_train_more))
attention_weights_more = nn.functional.softmax(-(X_repeat_more - x_train_more)**2 / 2, dim=1)
y_hat_more = torch.matmul(attention_weights_more, y_train_more)
plot_kernel_regv_more(y_hat_more)

d2l.show_heatmaps(attention_weights_more.unsqueeze(0).unsqueeze(0),xlabel='Sorted training inputs',ylabel='Sorted testing inputs')

(2)在带参数的注意力汇聚的实验中学习得到的参数 w w w 的价值是什么?为什么在可视化注意力权重时,它会使加权区域更加尖锐?
w w w 的价值在于放大注意力,也就是利用 softmax 函数的特性使键 x i x_i xi 和查询 x x x 距离小的得以保存,学习到的 w w w 就是掌握这个放大的尺度。
距离大的被过滤,当然也就显得更尖锐了。
(3)如何将超参数添加到非参数的Nadaraya-Watson核回归中以实现更好地预测结果?
加进去就能行。
n_train_test = 50
x_train_test, _ = torch.sort(torch.rand(n_train_test) * 5)def f(x):return 2 * torch.sin(x) + x**0.8y_train_test = f(x_train_test) + torch.normal(0.0, 0.5, (n_train_test,))
x_test_test = torch.arange(0, 5, 0.1)
y_truth_test = f(x_test_test)def plot_kernel_regv_more(y_hat_test):d2l.plot(x_test_test, [y_truth_test, y_hat_test], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])d2l.plt.plot(x_train_test, y_train_test, 'o', alpha=0.5);X_repeat_test = x_test_test.repeat_interleave(n_train_test).reshape((-1, n_train_test))
attention_weights_test = nn.functional.softmax(-((X_repeat_test - x_train_test)*net.w.detach().numpy())**2 / 2, dim=1) # 加入训练好的权重
y_hat_test = torch.matmul(attention_weights_test, y_train_test)
plot_kernel_regv_more(y_hat_test)

(4)为本节的核回归设计一个新的带参数的注意力汇聚模型。训练这个新模型并可视化其注意力权重。
不会,略。
相关文章:

《动手学深度学习 Pytorch版》 10.2 注意力汇聚:Nadaraya-Watson 核回归
import torch from torch import nn from d2l import torch as d2l1964 年提出的 Nadaraya-Watson 核回归模型是一个简单但完整的例子,可以用于演示具有注意力机制的机器学习。 10.2.1 生成数据集 根据下面的非线性函数生成一个人工数据集,其中噪声项 …...
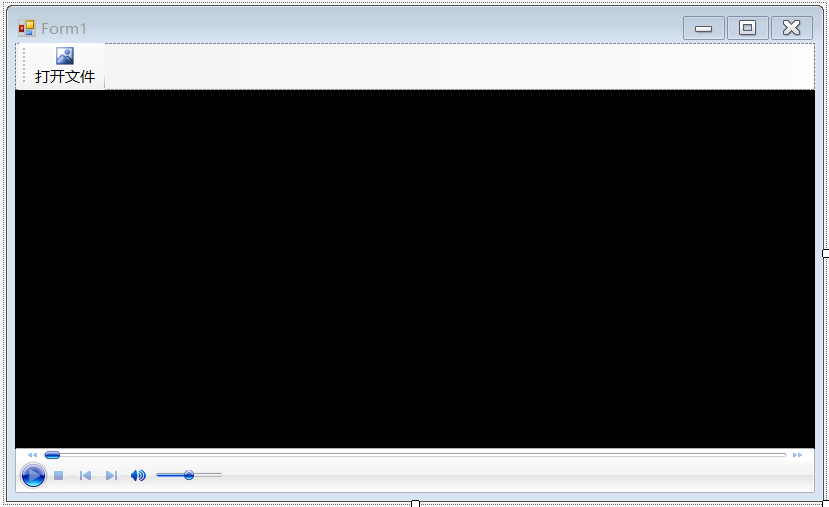
测试C#调用Windows Media Player组件
新建基于.net framework的Winform项目,可以通过添加引用的方式选择COM组件中的Windows Media Player组件,如下图所示: 也可以在VS2022的工具箱空白处点右键,选择“选择项…”菜单。 在弹出的选择工具箱项窗口中…...

面试经典150题——Day20
文章目录 一、题目二、题解 一、题目 14. Longest Common Prefix Write a function to find the longest common prefix string amongst an array of strings. If there is no common prefix, return an empty string “”. Example 1: Input: strs [“flower”,“flow”…...
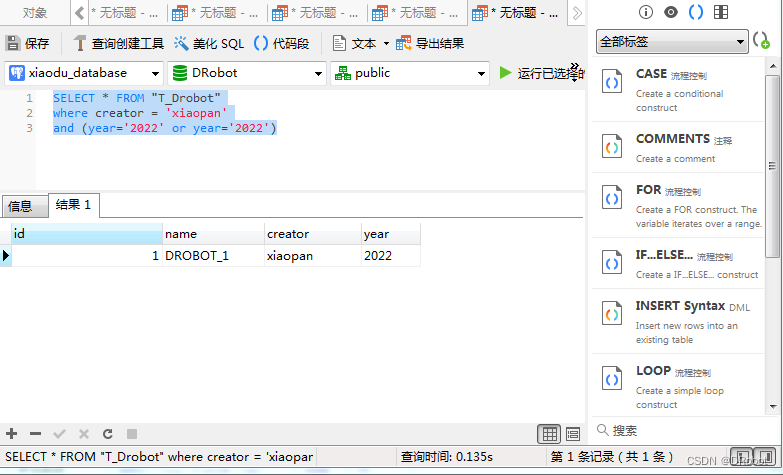
[SQL开发笔记]AND OR运算符复杂表达式开发实例
结合 AND & OR实例:通过圆括号使用and或or来组成复杂的表达式 目标数据库及表:使用 DRobot数据库,"T_Drobot" 表 假设我们需要查询"T_Drobot" 表,并从"T_Drobot"表中查询选取creator为 "…...

如何将本地 PDF 文件进行翻译
在日常工作和学习中,我们经常会遇到需要翻译 PDF 文件的情况。比如,我们需要将一份英文的技术文档翻译成中文,或者将一份中文的法律文件翻译成英文。 传统上,我们可以使用专业翻译软件或服务来翻译 PDF 文件。但是,这…...

Node.js的readline模块 命令行交互的模块
Node.js是一个非常流行的JavaScript运行时环境,它提供了许多内置模块来帮助我们开发应用程序。其中之一是readline模块,它提供了一种简单的方法来读取用户输入并进行交互。 本文将详细介绍readline模块的API和使用案例,并附有代码注释。 re…...

前沿重器[36] | ACL23-基于检索的大语言模型-报告阅读
前沿重器 栏目主要给大家分享各种大厂、顶会的论文和分享,从中抽取关键精华的部分和大家分享,和大家一起把握前沿技术。具体介绍:仓颉专项:飞机大炮我都会,利器心法我还有。(算起来,专项启动已经…...

2023秋招笔试算法Python3题解
诸神缄默不语-个人CSDN博文目录 签两方了,感觉秋招已经结束了,所以发布一下之前写的笔试编程题题解。 不全。可能有些题我会继续补。 不保证能过。 后续依然有可能继续刷算法题,但是就另外专门写博文来解析了。 打码是因为原则上其实是不让公…...
uniapp--点击上传图片到oss再保存数据给后端接口
项目采用uniapp与uview2.0组件库 --1.0的也可以参考一下,大差不差 一、项目要求与样式图 点击上传n张图片到oss,然后点击提交给后端 二、思路 1、打开上传按钮,弹出框内出现上传图片和提交按钮 2、点击上传图片区域,打开本地图…...
)
创建Secret(使用kubectl)
创建Secret(使用kubectl) 假设某个 Pod 需要访问数据库。在您执行 kubectl 命令所在机器的当前目录,创建文件 ./username.txt 文件和 ./password.txt 暂存数据库的用户名和密码,后续我们根据这两个文件配置 kubernetes secrets。…...

Notepad++正则查询替换操作
Notepad编辑器查找功能非常强大,本处记录一些实战中常用到复杂查询替换操作。 注意:如果是重要文件,替换操作前最好备份;当前一个操作后也可以用ctrlz恢复。 查找重复行 用查找(ctrlf)功能,用正则表达式模式匹配。 查…...

Hive特殊函数的使用
Hive特殊函数的使用 with ascastget_json_objectunix_timestampfrom_unixtime with as 在Hive中,WITH AS是一种子查询的用法,用于在查询的开头定义一个临时表达式。它的语法结构如下: WITH [表达式名称] AS (子查询表达式 )在这个结构中,[表…...
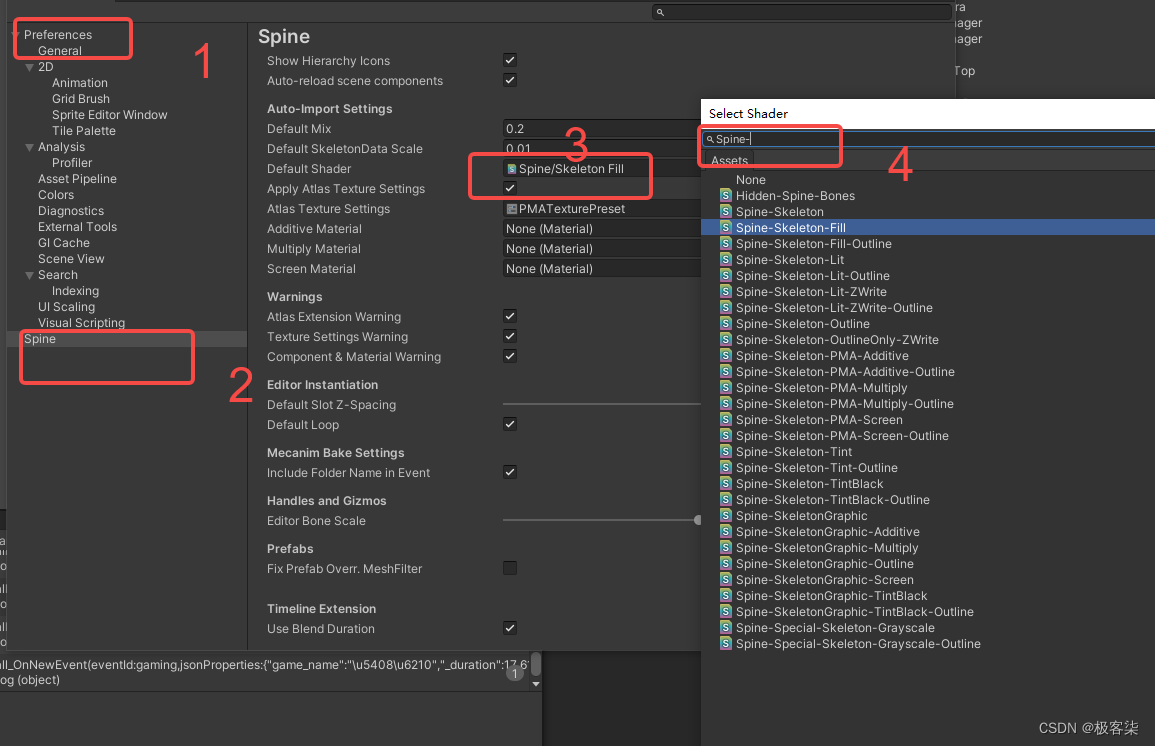
Unity Spine 指定导入新Spine动画的默认材质
指定导入新Spine动画的默认材质 找到Spine的Editor导入配置如何修改方法一: 你可以通过脚本 去修改Assets/Editor/SpineSettings.asset文件方法二:通过面板手动设置 找到Spine的Editor导入配置 通常在 Assets/Editor/SpineSettings.asset 配置文件对应着 Edit/Prefe…...
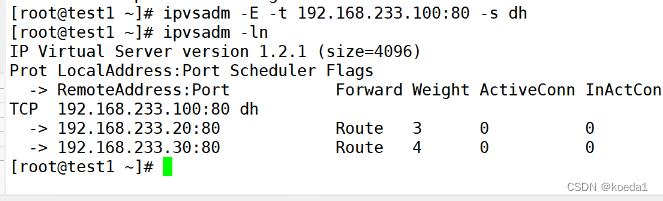
lvs负载均衡集群
目录 一、集群: 1、集群的目的: 2、集群的类型: 3、集群的可靠性指标: 4、设计集群时需要考虑的原则: 二、lvs集群: 1、lvs集群中的术语: 2、lvs访问的大致流程: 三、lvs的…...

MySQL---表的增查改删(CRUD基础)
文章目录 什么是CRUD?新增(Create)单行数据 全列插入多行数据 指定列插入 查询(Retrieve)全列查询指定列查询查询字段为表达式起别名查询去重查询排序查询条件查询分页查询 修改(Update)删除&…...
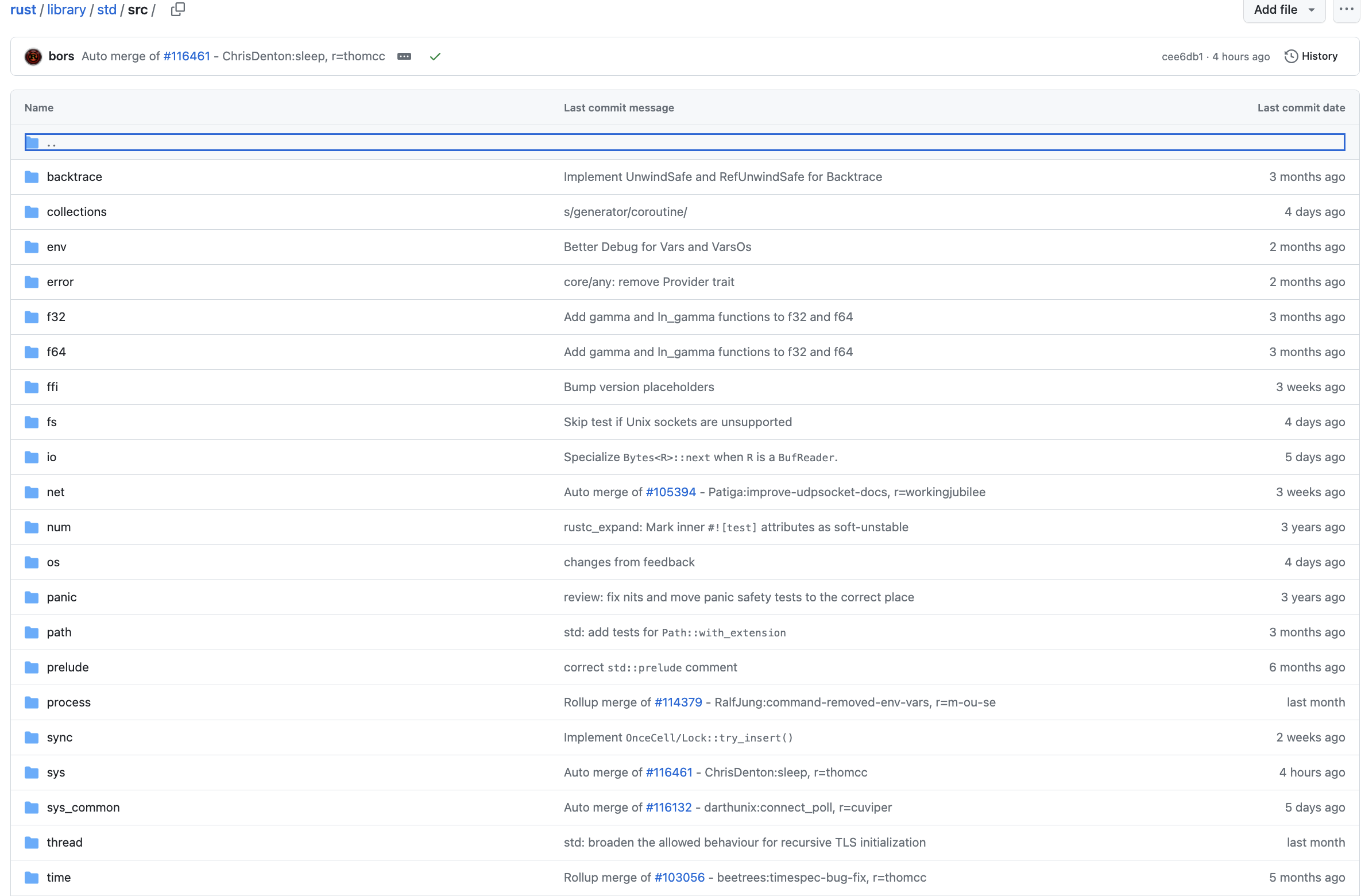
听GPT 讲Rust源代码--library/std(2)
File: rust/library/std/src/sys_common/wtf8.rs 在Rust源代码中,rust/library/std/src/sys_common/wtf8.rs这个文件的作用是实现了UTF-8编码和宽字符编码之间的转换,以及提供了一些处理和操作UTF-8编码的工具函数。 下面对这几个结构体进行一一介绍&…...

力扣第1005题 K 次取反后最大化的数组和 c++ 贪心 双思维
题目 1005. K 次取反后最大化的数组和 简单 相关标签 贪心 数组 排序 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以…...
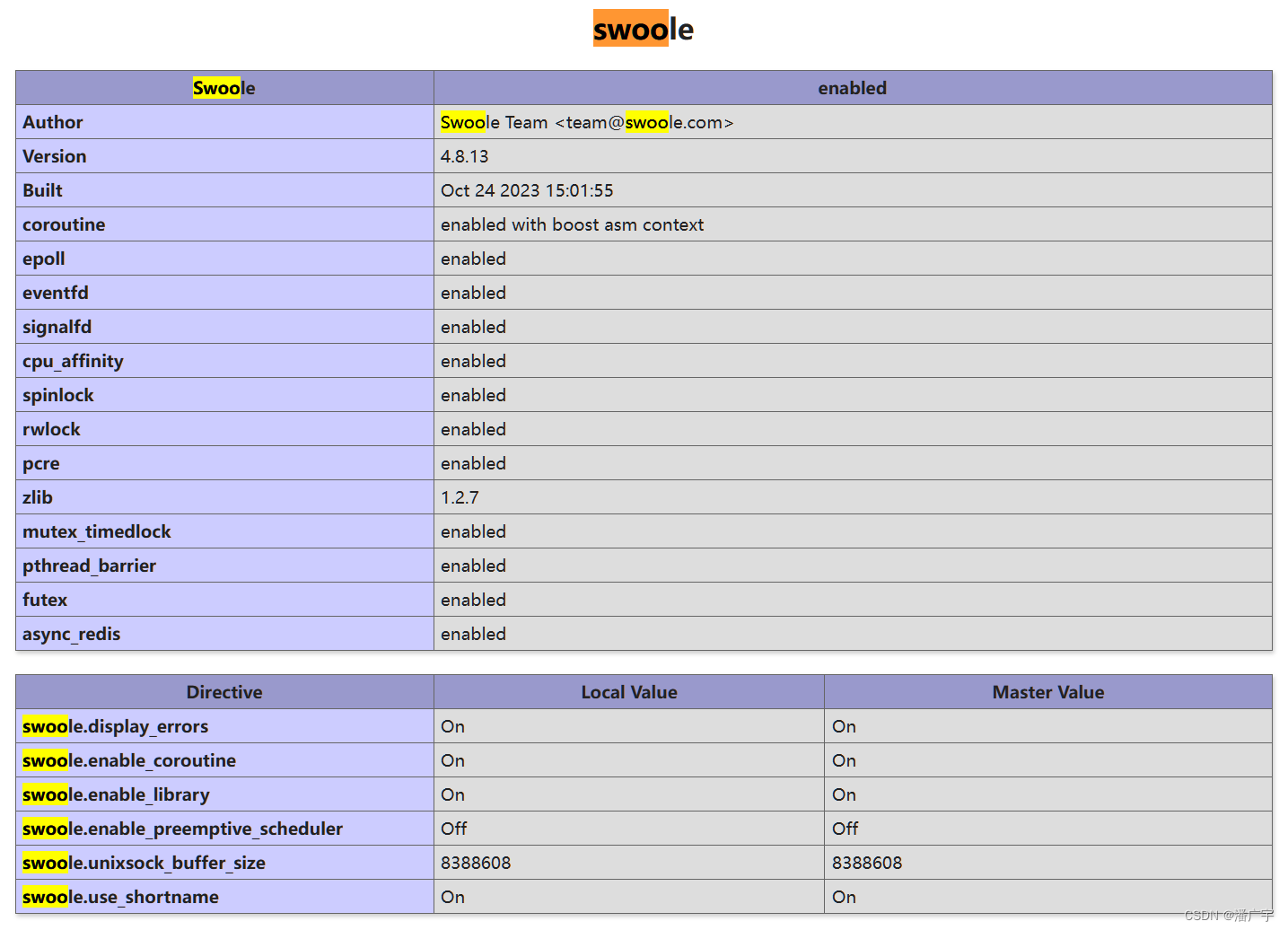
Swoole 4.8版本的安装
1、从github拉取安装包 Release v4.8.13 swoole/swoole-src GitHub 2、解压压缩包 tar -zxvf ./v4.8.13.tar.gzcd ./swoole-src-4.8.13 3、执行安装命令 phpize && \ ./configure && \ make && sudo make install 4、检查swoole模块是否安装完成…...
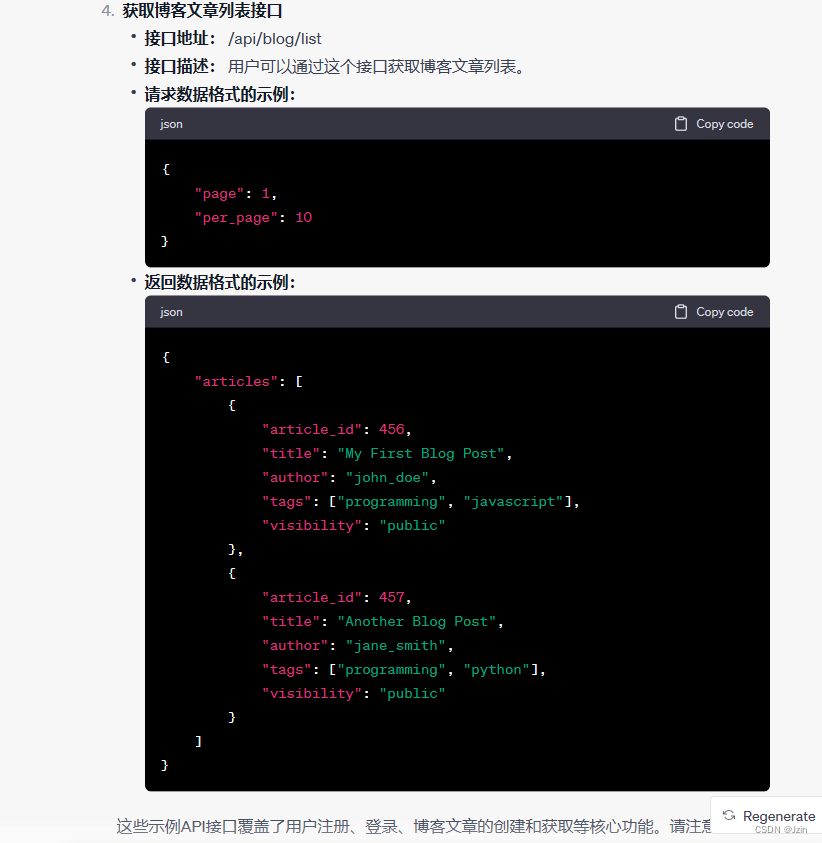
ChatGPT和Copilot协助Vue火速搭建博客网站
AI 对于开发人员的核心价值 网上会看到很多 AI 的应用介绍或者教程 使用 AI 聊天,咨询问题 —— 代替搜索引擎使用 AI 写各种的电商文案(淘宝、小红书)使用 AI 做一个聊天机器人 —— 这最多算猎奇、业余爱好、或者搞个套壳产品来收费 以上…...
javaEE -8(9000字详解网络编程)
一:网络编程基础 1.1 网络资源 所谓的网络资源,其实就是在网络中可以获取的各种数据资源,而所有的网络资源,都是通过网络编程来进行数据传输的。 用户在浏览器中,打开在线视频网站,如优酷看视频ÿ…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

【Elasticsearch基础】Elasticsearch批量操作(Bulk API)深度解析与实践指南
目录 1 Bulk API概述 1.1 什么是批量操作 1.2 Bulk API的优势 2 Bulk API的工作原理 2.1 请求处理流程 2.2 底层机制 3 Bulk API的使用方法 3.1 基本请求格式 3.2 操作类型示例 3.3 响应格式 4 Bulk API的最佳实践 4.1 批量大小优化 4.2 错误处理策略 4.3 性能调…...

低代码采购系统搭建:鲸采云+能源行业订单管理自动化案例
在能源行业数字化转型浪潮下,某大型能源集团通过鲸采云低代码平台,仅用3周时间就完成了采购订单管理系统的定制化搭建。本文将揭秘这一成功案例的实施路径与关键成效。 项目背景与挑战 该企业面临: 供应商分散:200供应商使用不同…...
