力扣第1005题 K 次取反后最大化的数组和 c++ 贪心 双思维
题目
1005. K 次取反后最大化的数组和
简单
相关标签
贪心 数组 排序
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
- 选择某个下标
i并将nums[i]替换为-nums[i]。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1 输出:5 解释:选择下标 1 ,nums 变为 [4,-2,3] 。
示例 2:
输入:nums = [3,-1,0,2], k = 3 输出:6 解释:选择下标 (1, 2, 2) ,nums 变为 [3,1,0,2] 。
示例 3:
输入:nums = [2,-3,-1,5,-4], k = 2 输出:13 解释:选择下标 (1, 4) ,nums 变为 [2,3,-1,5,4] 。
提示:
1 <= nums.length <= 104-100 <= nums[i] <= 1001 <= k <= 104
思路和解题方法
- 首先,我们需要对数组进行排序。由于是要使数组中的数尽可能地都为正数,因此我们应该把绝对值小的负数变为正数。
- 这样一来,负数的数量就会减少,而整数和零的数量就会增加,这有利于最终结果更接近最优解。
- 排序后,我们可以从小到大遍历数组,每当遇到一个负数,就将其取反,同时减少可取反的次数 k。
- 这里有个问题,如果我们仅仅只考虑绝对值最小的那个负数,需要取反多少次呢?显然,如果可取反的次数 k 为奇数,那么最终结果就是把绝对值最小的那个负数取反,而如果可取反的次数 k 为偶数,则不需要取反它。
- 另一方面,如果可取反的次数 k 为偶数,那么显然数组中所有的数都会保持不变。最后,我们只需简单地处理一下数组的和即可。
复杂度
时间复杂度:
O(n * logn)
时间复杂度:排序的时间复杂度为 O(nlogn),for 循环的时间复杂度为 O(n),因此总的时间复杂度为 O(nlogn + nlogn + n) = O(nlogn)。
空间复杂度
O(1)
空间复杂度:除了输入的数组外,算法只涉及到常量级别的额外空间。因此空间复杂度为 O(1)。
c++ 代码一
class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(), nums.end()); // 对数组进行排序,使得负数排在前面int min1 = 1000; // 初始化绝对值最小的元素为一个较大的数int min2 = 0; // 记录绝对值最小的元素的索引for (int i=0; i<nums.size(); i++) {if(abs(nums[i]) <= min1) { // 如果当前元素的绝对值小于等于min1min1 = abs(nums[i]); // 更新min1为当前元素的绝对值min2 = i; // 记录绝对值最小的元素的索引}if(nums[i] < 0 && k > 0) { // 如果当前元素是负数且还有剩余的翻转次数nums[i] *= -1; // 将当前元素取反k--; // 翻转次数k减一}}if(k%2 == 1) // 如果剩余的翻转次数是奇数nums[min2] *= -1; // 将绝对值最小的元素取反int ans = 0;for(int n : nums)ans += n; // 计算数组中所有元素的和return ans; // 返回最终的数组和作为结果}
};
思路和解题方法二
- 对数组进行排序
排序函数中采用自定义比较器的方式,把按照绝对值从大到小进行排序。这样排序后,数组中绝对值最大的元素会排在数组的最末尾,而绝对值最小的元素则会排在数组的最前面。
- 取反负数
遍历数组,如果当前的元素是负数,那么就把它取反(变为正数),同时将剩余可取反次数减一。注意我们要在剩余可取反次数大于 0 且当前元素是负数的情况下才能取反。
- 处理无法取反的情况
如果我们完成了步骤 2 后,还有剩余可取反的次数,但已经不存在可以被取反的元素了,那么我们需要对数组进行调整,使得我们所取反的元素的绝对值最小。具体地说,我们需要在数组的最末尾找到一个元素,并将它取反。因为这个元素绝对值最大,所以取反后对原来的和的影响最小。由于我们对数组进行了排序,因此直接访问最末尾的元素即可。
- 计算数组的和
遍历整个数组,计算所有元素之和即可。最终的和就是我们的答案。
复杂度
时间复杂度:
O(n * logn)
时间复杂度:排序的时间复杂度为 O(nlogn),for 循环的时间复杂度为 O(n),因此总的时间复杂度为 O(nlogn + nlogn + n) = O(nlogn)。
空间复杂度
O(1)
空间复杂度:除了输入的数组外,算法只涉及到常量级别的额外空间。因此空间复杂度为 O(1)。
c++ 代码二
class Solution {// 定义排序比较器,按照绝对值从大到小排序static bool cmp(int a, int b) {return abs(a) > abs(b);}
public:int largestSumAfterKNegations(vector<int>& A, int K) {sort(A.begin(), A.end(), cmp); // 第一步:对数组进行排序for (int i = 0; i < A.size(); i++) { // 第二步:取反负数if (A[i] < 0 && K > 0) {A[i] *= -1;K--;}}if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步:处理无法取反的情况int result = 0;for (int a : A) result += a; // 第四步:计算数组和return result;}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第1005题 K 次取反后最大化的数组和 c++ 贪心 双思维
题目 1005. K 次取反后最大化的数组和 简单 相关标签 贪心 数组 排序 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以…...
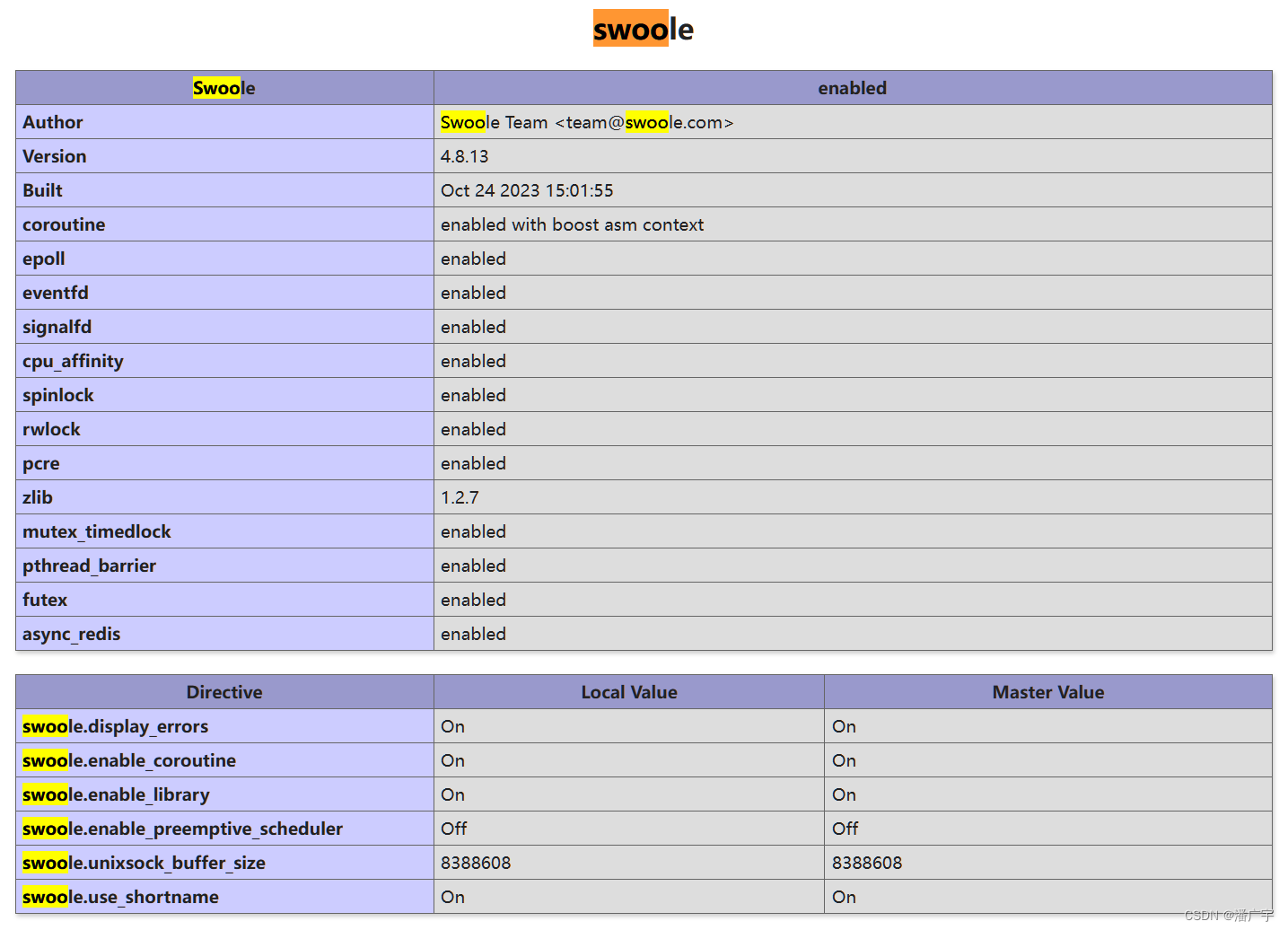
Swoole 4.8版本的安装
1、从github拉取安装包 Release v4.8.13 swoole/swoole-src GitHub 2、解压压缩包 tar -zxvf ./v4.8.13.tar.gzcd ./swoole-src-4.8.13 3、执行安装命令 phpize && \ ./configure && \ make && sudo make install 4、检查swoole模块是否安装完成…...
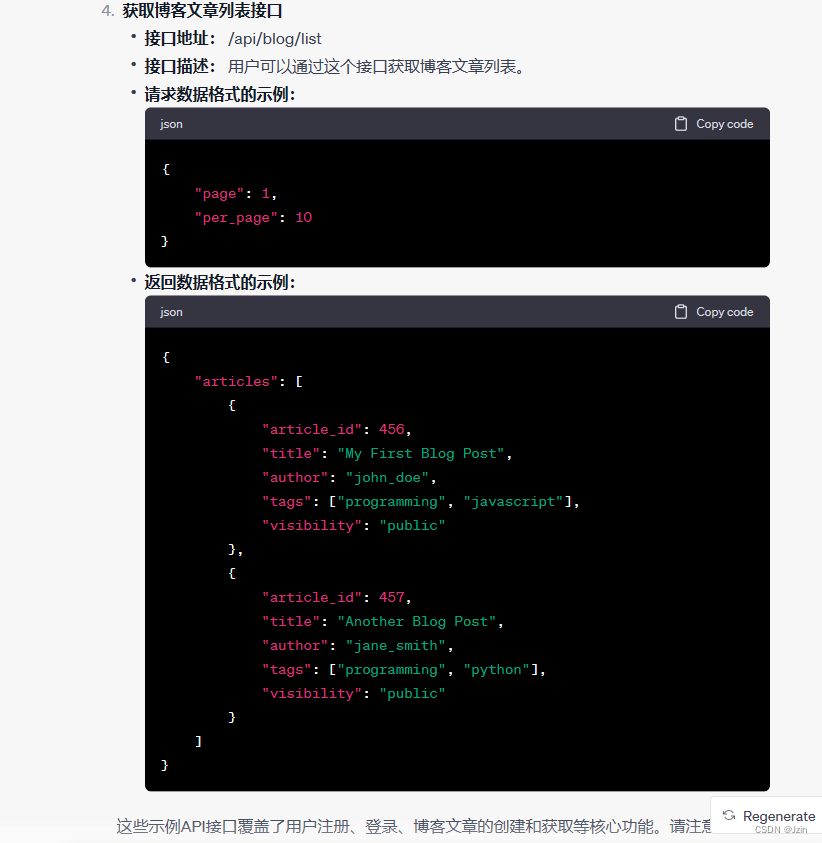
ChatGPT和Copilot协助Vue火速搭建博客网站
AI 对于开发人员的核心价值 网上会看到很多 AI 的应用介绍或者教程 使用 AI 聊天,咨询问题 —— 代替搜索引擎使用 AI 写各种的电商文案(淘宝、小红书)使用 AI 做一个聊天机器人 —— 这最多算猎奇、业余爱好、或者搞个套壳产品来收费 以上…...
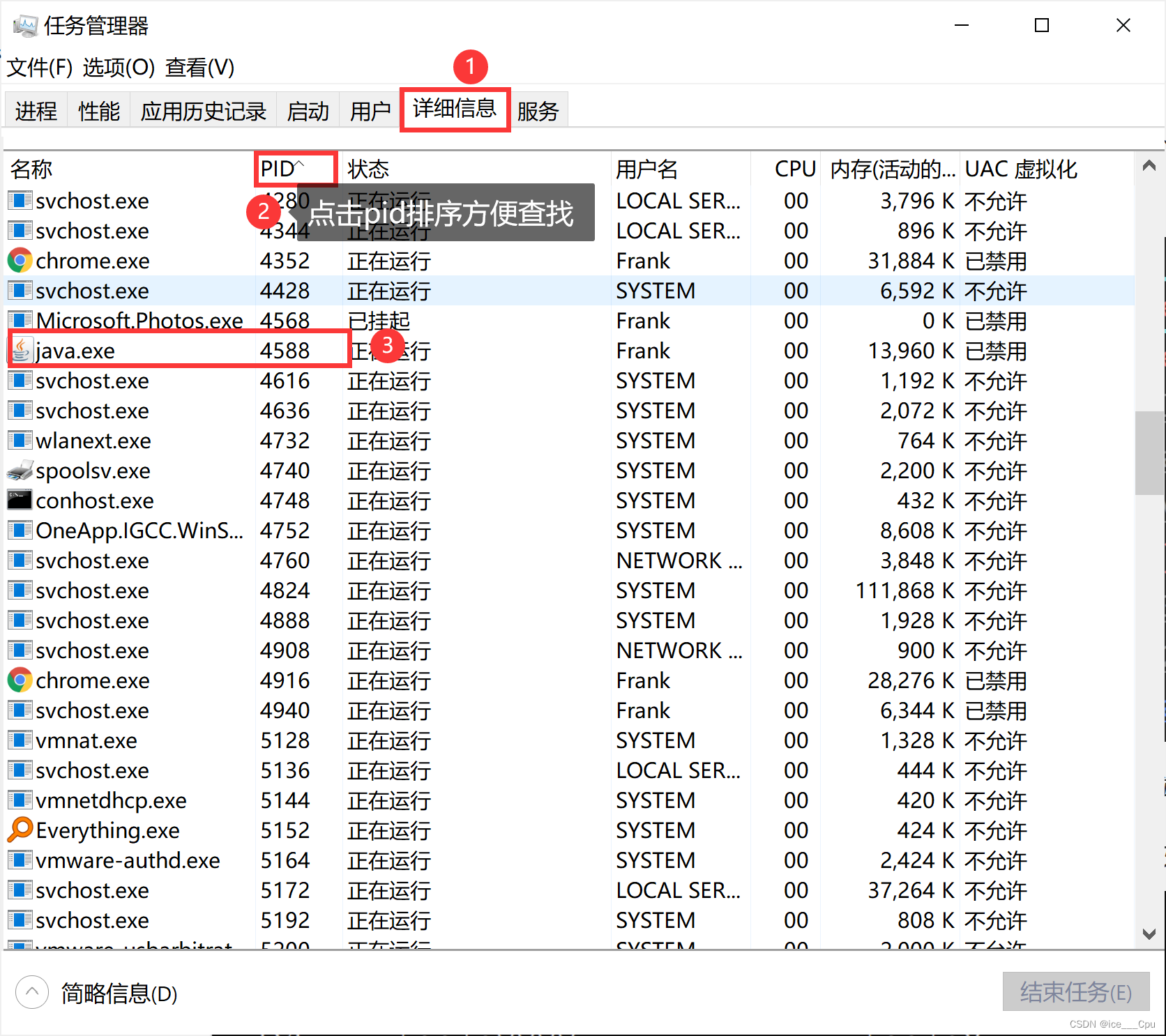
javaEE -8(9000字详解网络编程)
一:网络编程基础 1.1 网络资源 所谓的网络资源,其实就是在网络中可以获取的各种数据资源,而所有的网络资源,都是通过网络编程来进行数据传输的。 用户在浏览器中,打开在线视频网站,如优酷看视频ÿ…...
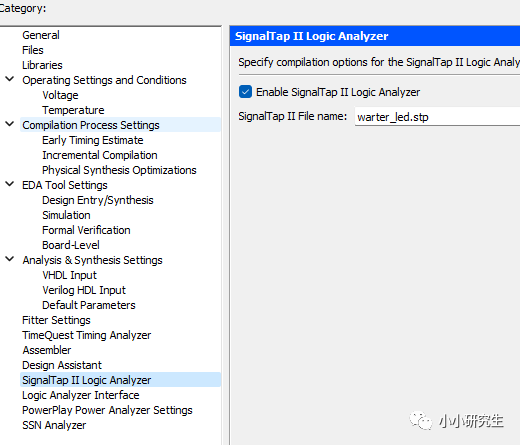
FPGA从入门到精通(二十)SignalTapII
这一篇将介绍SignalTapII。 之前的工程我们是做仿真,设置激励,观察输出波形去判断代码没有问题,但事实上我们真实的需求是综合后的代码下载到FPGA芯片中能够符合预期。 其中可能出现问题的原因有: 1、我们是写testbench设置激励…...

RHCE---shell 条件测试
文章目录 目录 文章目录 前言 一.条件测试 概述: 文件测试 整数测试: 总结 前言 当我们完成某一命令的编写时,除了观察输出的内容,我们又如何得知命令是否执行成功呢? 这里,我们需要用到条件测试 一.条…...
Linux下QT打开文件选择对话框时,程序报错退出
系统:Ubuntu QString fileName QFileDialog::getOpenFileName(this, "open", "./", "document Files (*.pdf)"); 调用该语句弹出文件对话框时,程序崩溃退出 错误提示: (Widget:5272): Gtk-WARNING **: 14…...

PyTorch中的intrusive_ptr
PyTorch中的intrusive_ptr 前言 intrusive_ptr與unique_ptr,shared_ptr等一樣,都是smart pointer。但是intrusive_ptr比較特別,它所指向的物件類型必須繼承自intrusive_ptr_target,而intrusive_ptr_target必須實現引用計數相關的…...

webrtc-stream编译报错记录
磁盘空间不足错误 错误信息 677.2 fatal: cannot create directory at blink/web_tests/external/wpt: No space left on device说明:这个错误是由于本地在配置docker资源时所给磁盘空间太小导致,直接根据镜像大小合理分配资源大小即可 pushd和popd执…...

什么是Docker CLI
Docker CLI(命令行界面)是一个工具,允许用户通过命令行或终端与Docker进行交互。Docker是一个开源平台,用于开发、运送和运行应用程序。Docker使用容器化技术来打包应用程序及其依赖项,以确保在不同环境中的一致性和隔…...

Java项目_家庭记账(简易版)
文章目录 简介代码实现 简介 该项目主要用来练习,Java的变量,运算符,分支结构和循环结构的知识点。 程序界面如下: 登记收入 登记支出 收支明细 程序退出 代码实现 package project;import java.util.Scanner;import sta…...

vscode json文件添加注释报错
在vscode中创建json文件,想要注释一波时,发现报了个错:Comments are not permitted in JSON. (521),意思是JSON中不允许注释 以下为解决方法: 在vscode的右下角中找到这个,点击 在出现的弹窗中输入json wit…...

vue3移动端嵌入pdf的两种办法
1.使用embed嵌入 好处:简单,代码量少,功能齐全 缺点:有固定样式,难以修改,不可定制 <embed class"embedPdf" :src"pdfurl" type"application/pdf">2.使用vue-pdf-e…...

中文编程开发语言工具系统化教程初级1上线
中文编程系统化教程初级1 学习编程捷径:(不论是正在学习编程的大学生,还是IT人士或者是编程爱好者,在学习编程的过程中用正确的学习方法 可以达到事半功倍的效果。对于初学者,可以通过下面的方法学习编程,…...

零售数据分析模板分享(通用型)
零售数据来源多,数据量大,导致数据的清洗整理工作量大,由于零售的特殊性,其指标计算组合更是多变,进一步导致了零售数据分析工作量激增,往往很难及时分析数据,发现问题。那怎么办?可…...
Spring Cloud之微服务
目录 微服务 微服务架构 微服务架构与单体架构 特点 框架 总结 SpringCloud 常用组件 与SpringBoot关系 版本 微服务 微服务:从字面上理解即:微小的服务; 微小:微服务体积小,复杂度低,一个微服…...
之date)
Linux命令(104)之date
linux命令之date 1.date介绍 linux命令date用来设置和显示系统日期和时间 2.date用法 date [参数] date参数 参数说明-s修改并设置时间-d可以显示以前和未来的时间%H小时%M分钟%S秒%X等价于%H %M %S%F显示当前所有时间属性%Y完整年份%m月%d日%A星期的全称 3.实例 3.1.当前…...
微信小程序投票管理系统:打造智能、便捷的投票体验
前言 随着社交网络的兴起和移动互联网的普及,人们对于参与和表达意见的需求越来越强烈。在这个背景下,微信小程序投票管理系统应运而生。它为用户提供了一个智能、便捷的投票平台,使用户可以轻松创建和参与各种类型的投票活动。本文将详细介…...
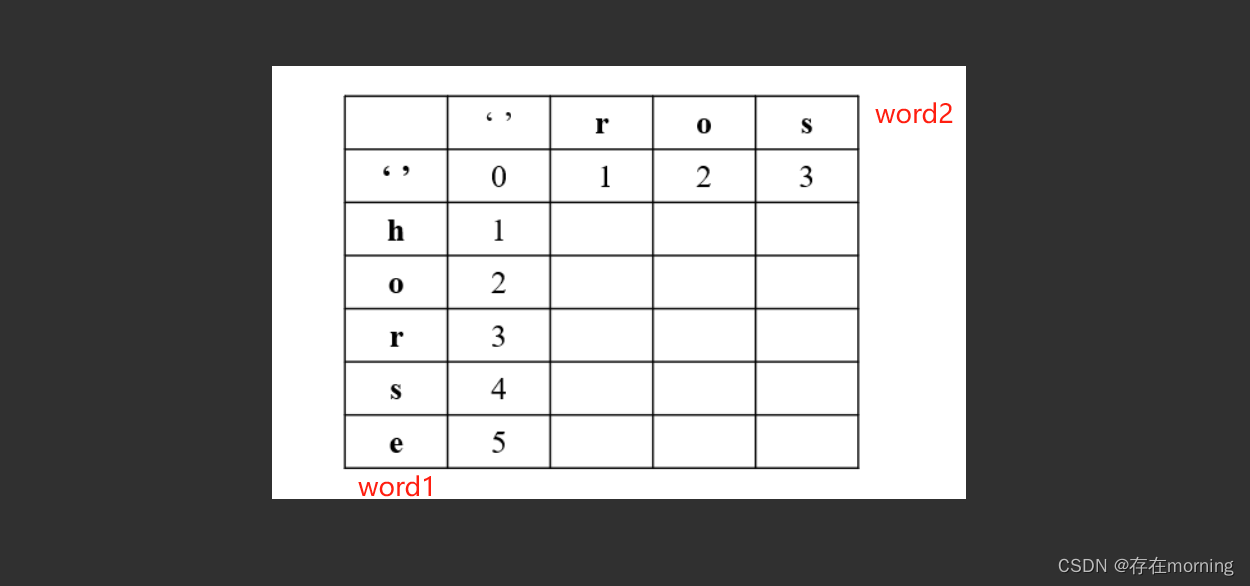
【算法训练-动态规划 五】【二维DP问题】编辑距离
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【动态规划】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...
Windows电脑如何录制电脑桌面?
如果你使用的电脑是Windows系统,那你是不是想知道如何在Windows电脑上录制电脑桌面? 本文以win10为例,好消息是,Windows 10电脑自带录屏工具,你可以直接使用此录屏工具轻松录制视频,而无需下载其他第三方软…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
