【算法训练-动态规划 五】【二维DP问题】编辑距离
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【动态规划】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。
明确目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
编辑距离【HARD】
终于又来到一道看了很久的高频题目这里
题干
搞定了一系列的简单题,来个编辑距离练练手
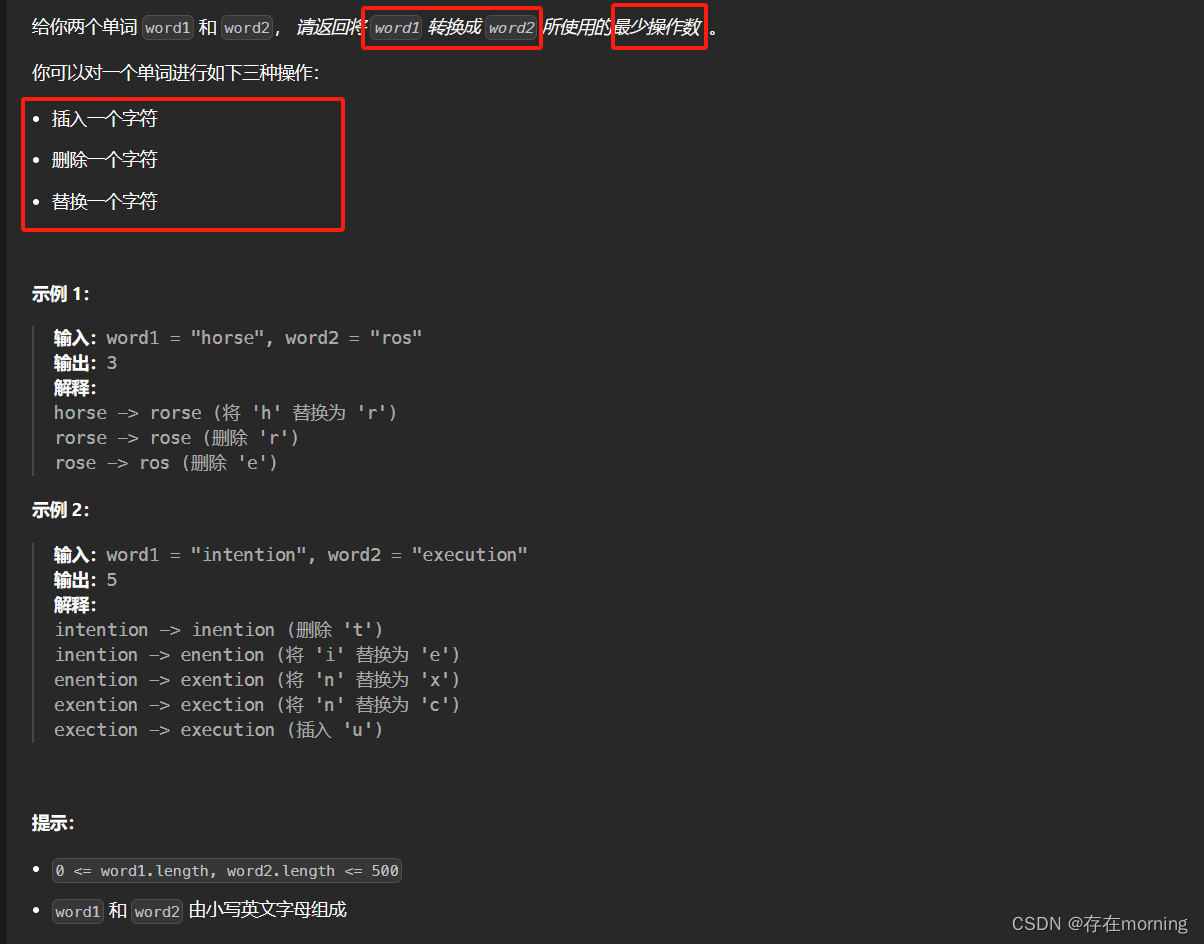
解题思路
原题解地址,解决两个字符串的动态规划问题,一般都是用两个指针 i, j 分别指向两个字符串的最后,然后一步步往前移动,缩小问题的规模
设两个字符串分别为 rad 和 apple,为了把 s1 变成 s2,算法会这样进行

暴力递归
base case 是 i 走完 s1 或 j 走完 s2,可以直接返回另一个字符串剩下的长度。对于每对儿字符 s1[i] 和 s2[j],可以有四种操作:
if s1[i] == s2[j]:啥都别做(skip)i, j 同时向前移动
else:三选一:插入(insert)删除(delete)替换(replace)有这个框架,问题就已经解决了。读者也许会问,这个「三选一」到底该怎么选择呢?很简单,全试一遍,哪个操作最后得到的编辑距离最小,就选谁
int minDistance(String s1, String s2) {int m = s1.length(), n = s2.length();// i,j 初始化指向最后一个索引return dp(s1, m - 1, s2, n - 1);
}// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
int dp(String s1, int i, String s2, int j) {// base caseif (i == -1) return j + 1;if (j == -1) return i + 1;if (s1.charAt(i) == s2.charAt(j)) {return dp(s1, i - 1, s2, j - 1); // 啥都不做}return min(dp(s1, i, s2, j - 1) + 1, // 插入dp(s1, i - 1, s2, j) + 1, // 删除dp(s1, i - 1, s2, j - 1) + 1 // 替换);
}int min(int a, int b, int c) {return Math.min(a, Math.min(b, c));
}情况一:什么都不做
if s1[i] == s2[j]:return dp(s1, i - 1, s2, j - 1); # 啥都不做
# 解释:
# 本来就相等,不需要任何操作
# s1[0..i] 和 s2[0..j] 的最小编辑距离等于
# s1[0..i-1] 和 s2[0..j-1] 的最小编辑距离
# 也就是说 dp(i, j) 等于 dp(i-1, j-1)如果 s1[i] != s2[j],就要对三个操作递归了
情况二:插入操作
dp(s1, i, s2, j - 1) + 1, # 插入
# 解释:
# 我直接在 s1[i] 插入一个和 s2[j] 一样的字符
# 那么 s2[j] 就被匹配了,前移 j,继续跟 i 对比
# 别忘了操作数加一
插入操作

情况三:删除操作
dp(s1, i - 1, s2, j) + 1, # 删除
# 解释:
# 我直接把 s[i] 这个字符删掉
# 前移 i,继续跟 j 对比
# 操作数加一
情况四:替换操作
dp(s1, i - 1, s2, j - 1) + 1 # 替换
# 解释:
# 我直接把 s1[i] 替换成 s2[j],这样它俩就匹配了
# 同时前移 i,j 继续对比
# 操作数加一
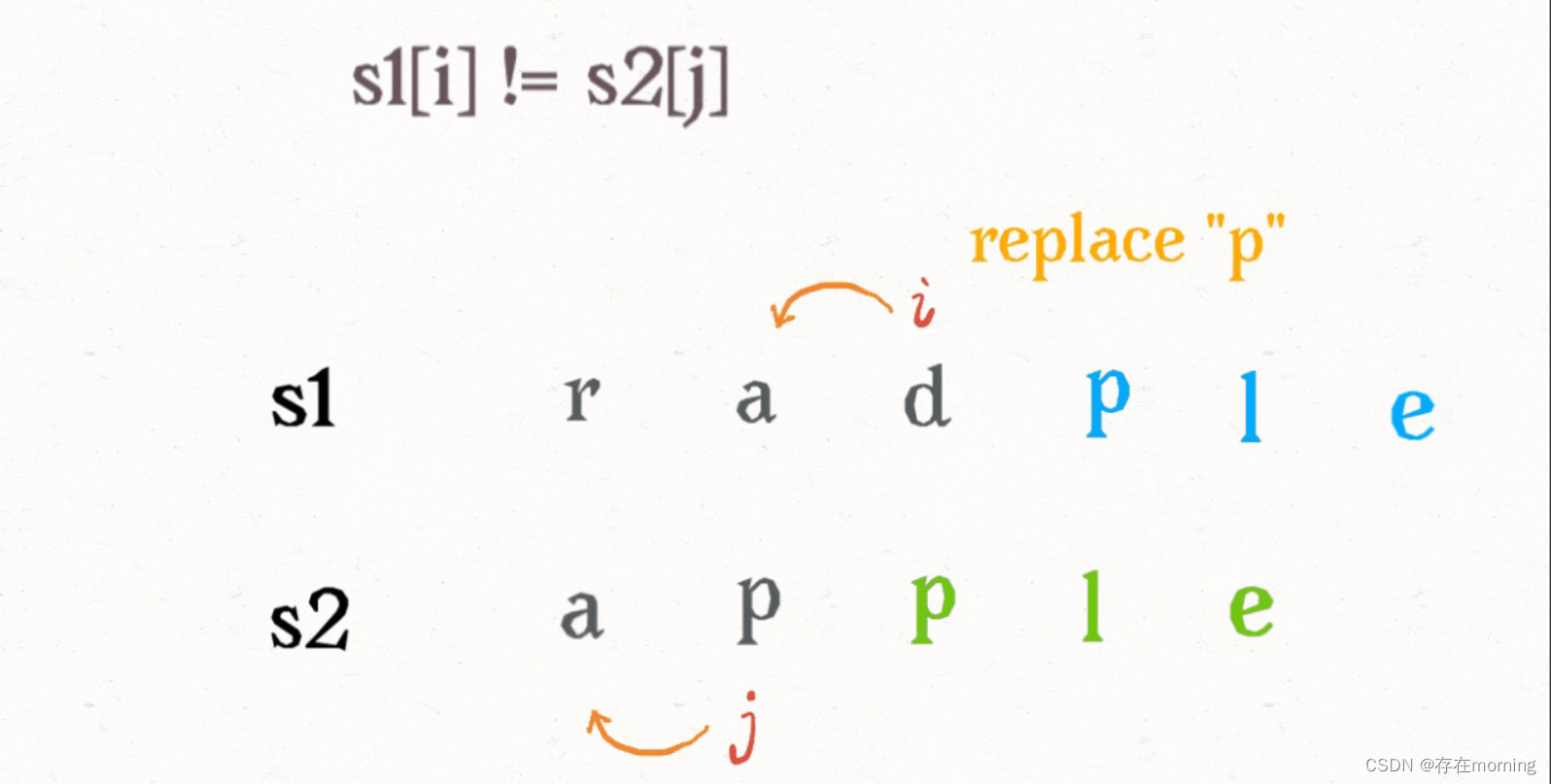
a字符被替换为p字符

int dp(i, j) {dp(i - 1, j - 1); // #1dp(i, j - 1); // #2dp(i - 1, j); // #3
}对于子问题 dp(i-1, j-1),如何通过原问题 dp(i, j) 得到呢?有不止一条路径,比如 dp(i, j) -> #1 和 dp(i, j) -> #2 -> #3。一旦发现一条重复路径,就说明存在巨量重复路径,也就是重叠子问题
动态规划
接下来用DP table来优化一下,降低重复子问题,首先明确 dp 数组的含义,dp 数组是一个二维数组,长这样
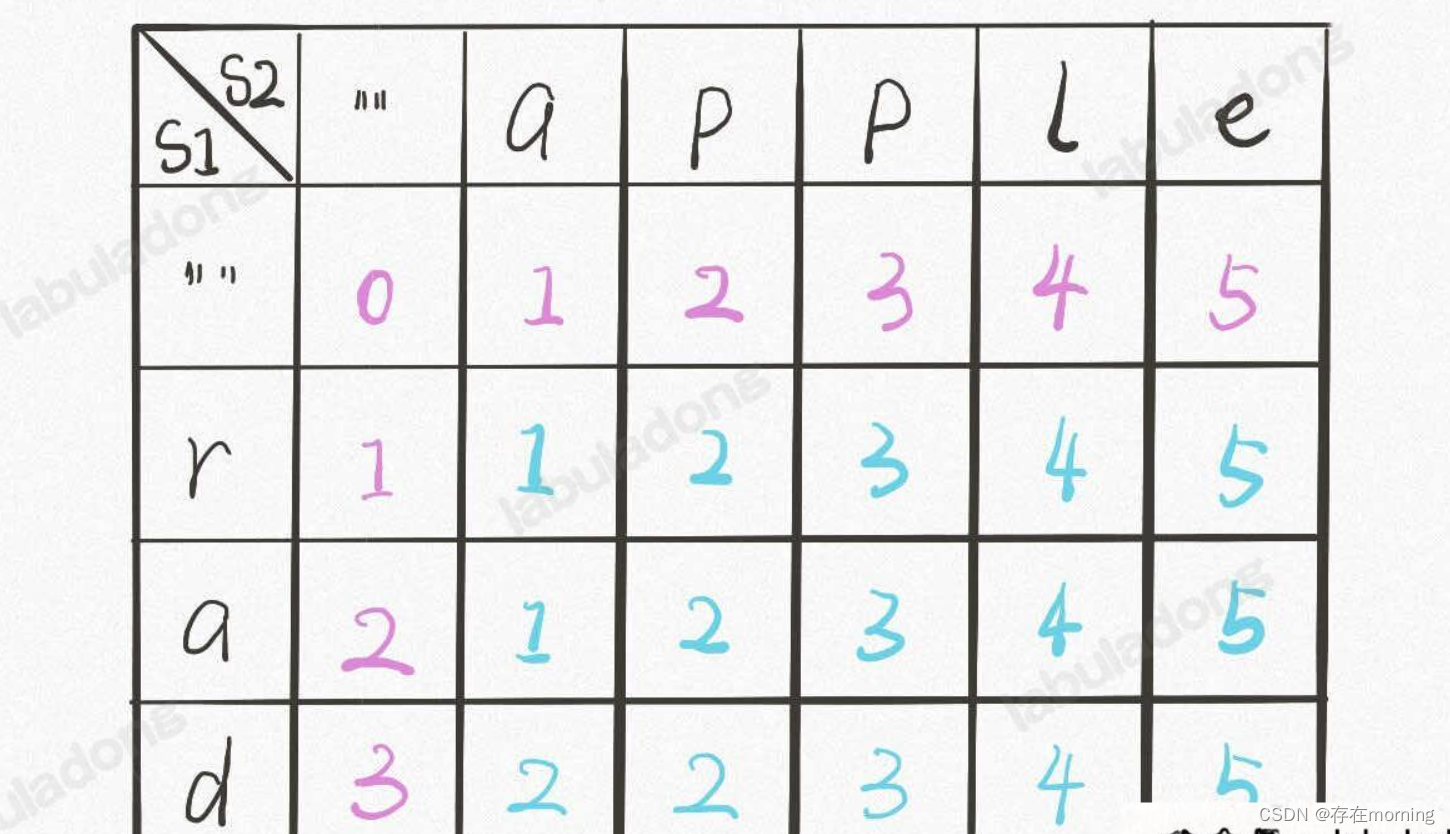
有了之前递归解法的铺垫,应该很容易理解。dp[..][0] 和 dp[0][..] 对应 base case,dp[i][j] 的含义和之前的 dp 函数类似
- 替换操作:word1的
0~i-1位置与word2的0~j-1位置的字符都相同,只是当前位置的字符不匹配,进行替换操作后两者变得相同dp[i-1][j-1]表示需要进行替换操作才能转到dp[i][j], 所以此时dp[i][j]=dp[i-1][j-1]+1(这个加1代表执行替换操作) - 删除操作: 若此时word1的
0~i-1位置与word2的0~j位置已经匹配了,此时多出了word1的i位置字符,应把它删除掉,才能使此时word1的0~i(这个i是执行了删除操作后新的i)和word2的0~j位置匹配,因此此时dp[i][j]=dp[i-1][j]+1(这个加1代表执行删除操作) - 插入操作:若此时word1的
0~i位置只是和word2的0~j-1位置匹配,此时只需要在原来的i位置后面插入一个和word2的j位置相同的字符使得此时的word1的0~i(这个i是执行了插入操作后新的i)和word2的0~j匹配得上,所以此时dp[i][j]=dp[i][j-1]+1(这个加1代表执行插入操作)
有了之前递归解法的铺垫,应该很容易理解。dp[..][0] 和 dp[0][..] 对应 base case,dp[i][j] 的含义和之前的 dp 函数类似
int dp(String s1, int i, String s2, int j)
// 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
dp 函数的 base case 是 i, j 等于 -1,而数组索引至少是 0,所以 dp 数组会偏移一位
dp[i-1][j-1]
// 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离
既然 dp 数组和递归 dp 函数含义一样,也就可以直接套用之前的思路写代码,唯一不同的是,DP table 是自底向上求解,递归解法是自顶向下求解
int minDistance(String s1, String s2) {int m = s1.length(), n = s2.length();// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp[i+1][j+1]int[][] dp = new int[m + 1][n + 1];// base case for (int i = 1; i <= m; i++)dp[i][0] = i;for (int j = 1; j <= n; j++)dp[0][j] = j;// 自底向上求解for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (s1.charAt(i-1) == s2.charAt(j-1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1,dp[i][j - 1] + 1,dp[i - 1][j - 1] + 1);}}}// 储存着整个 s1 和 s2 的最小编辑距离return dp[m][n];
}int min(int a, int b, int c) {return Math.min(a, Math.min(b, c));
}代码实现
给出代码实现基本档案
基本数据结构:数组
辅助数据结构:无
算法:动态规划
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
class Solution
{// 编辑距离,返回两个字符串操作的最小距离public int minDistance(String word1, String word2){// 1 入参校验if(word1.length() < 1 && word2.length() < 1){return 0;}// 2 定义行列长度,word1作为竖,word2作为行int m = word1.length();int n = word2.length();// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp[i+1][j+1]int[][] dp = new int[m + 1][n + 1];// 4 初始化base casefor(int i = 1; i <= m; i++){dp[i][0] = i;}for(int j = 1; j <= n; j++){dp[0][j] = j;}// 5 状态转移方程:自底向上求解,从头开始比较,i=0和j=0的位置初始化为基本操作数for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i - 1][j - 1];}else{dp[i][j] = minCompare(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1);}}}return dp[m][n];}private int minCompare(int a, int b, int c){return Math.min(a, Math.min(b, c));}
}
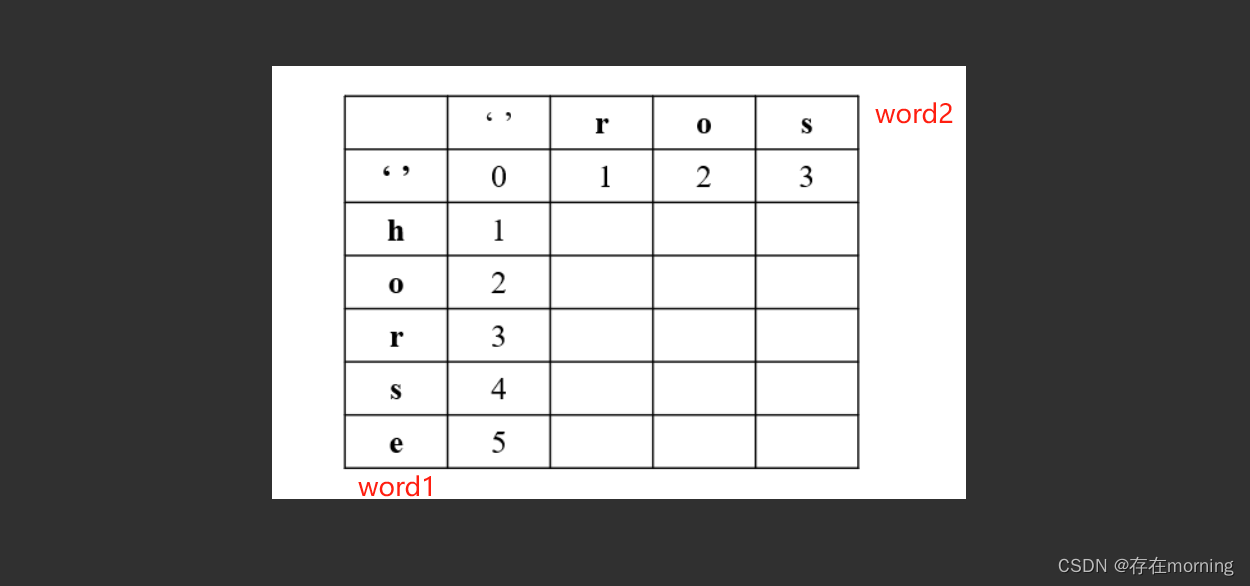
- 第一行,是 word1 为空,变成 word2 最少步数,就是插入操作
- 第一列,是 word2 为空,word1要变为word2(也就是空)需要的最少步数,就是删除操作
(一)、当word1[i]==word2[j]时,由于遍历到了i和j,说明word1的0~i-1和word2的0~j-1的匹配结果已经生成,
由于当前两个字符相同,因此无需做任何操作,dp[i][j]=dp[i-1][j-1](二)、当word1[i]!=word2[j]时,可以进行的操作有3个:① 替换操作:可能word1的0~i-1位置与word2的0~j-1位置的字符都相同,只是当前位置的字符不匹配,进行替换操作后两者变得相同,所以此时dp[i][j]=dp[i-1][j-1]+1(这个加1代表执行替换操作)②删除操作:若此时word1的0~i-1位置与word2的0~j位置已经匹配了,此时多出了word1的i位置字符,应把它删除掉,才能使此时word1的0~i(这个i是执行了删除操作后新的i)和word2的0~j位置匹配,因此此时dp[i][j]=dp[i-1][j]+1(这个加1代表执行删除操作)③插入操作:若此时word1的0~i位置只是和word2的0~j-1位置匹配,此时只需要在原来的i位置后面插入一个和word2的j位置相同的字符使得此时的word1的0~i(这个i是执行了插入操作后新的i)和word2的0~j匹配得上,所以此时dp[i][j]=dp[i][j-1]+1(这个加1代表执行插入操作)④由于题目所要求的是要最少的操作数:所以当word1[i] != word2[j] 时,需要在这三个操作中选取一个最小的值赋格当前的dp[i][j]
(三)总结:状态方程为:
if(word1[i] == word2[j]):dp[i][j] = dp[i-1][j-1]
else:min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1PS:大佬的代码中word1.charAt(i-1)==word2.charAt(j-1)的原因是:初始化DP Table时dp[i][0]和dp[0][j]已经填写完成,所以接下来填表需要从1开始,但是字符的比较需要从0开始,因此才这样子写
复杂度分析
时间复杂度:O(N^2),这里 N 是数组的长度,我们写了两个 for 循环,每个 for 循环的时间复杂度都是线性的;
空间复杂度:O(N),要使用和输入数组长度相等的状态数组,因此空间复杂度是 O(N)。
相关文章:

【算法训练-动态规划 五】【二维DP问题】编辑距离
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【动态规划】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...
Windows电脑如何录制电脑桌面?
如果你使用的电脑是Windows系统,那你是不是想知道如何在Windows电脑上录制电脑桌面? 本文以win10为例,好消息是,Windows 10电脑自带录屏工具,你可以直接使用此录屏工具轻松录制视频,而无需下载其他第三方软…...
ubuntu18.04双系统安装(2023最新最详细)以及解决重启后发现进不了Ubuntu问题
目录 一.简介 二.安装教程 1.首先确定了电脑的引导格式是UEFIGPT还是BIOSMBR 2. 使用Windows磁盘管理划分足够的磁盘空间 3. 开始安装 三.重启后发现自动进入WIN10系统了,进不了Ubuntu? 一.简介 Linux是一种自由和开放源代码的操作系统内核&#x…...

Springboot + screw 数据库快速开发文档
1、方式1 引入依赖 <dependency><groupId>cn.smallbun.screw</groupId><artifactId>screw-core</artifactId><version>1.0.5</version></dependency> /*** 文档生成 Springboot2.X screw数据库快速开发文档(74&…...

2 第一个Go程序
概述 在上一节的内容中,我们介绍了Go的前世今生,包括:Go的诞生、发展历程、特性和应用领域。从本节开始,我们将正式学习Go语言。Go语言是一种编译型语言,也就是说,Go语言在运行之前需要先进行编译ÿ…...

Leetcode—2678.老人的数目【简单】
2023每日刷题(八) Leetcode—2678.老人的数目 int countSeniors(char ** details, int detailsSize){ int ans 0; int i; int tens 0; int ones 0; for(i 0; i < detailsSize; i) { tens ((details i) 11) - ‘0’; ones ((details i) 12)…...
解决 /bin/bash^M: bad interpreter: No such file or directory
问题描述 linux 系统中知行*.sh 文件报/bin/bash^M: bad interpreter: No such file or directory 原因: .sh文件是在windows系统编写的,在linux执行就有问题 解决过程 转化下格式执行如下命令 # dos2unix app.sh 结果bash: dos2unix: command not …...
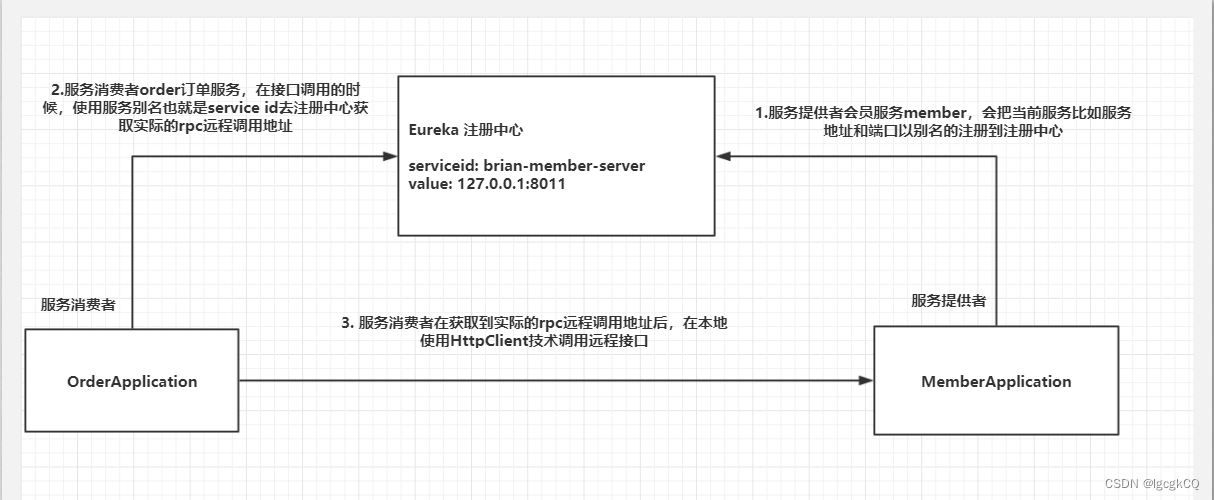
Spring Cloud之服务注册与发现(Eureka)
目录 Eureka 介绍 角色 实现流程 单机构建 注册中心 服务提供者 服务消费者 集群搭建 注册中心 服务提供者 自我保护机制 原理分析 Eureka 介绍 Eureka是spring cloud中的一个负责服务注册与发现的组件,本身是基于REST的服务,同时还提供了…...
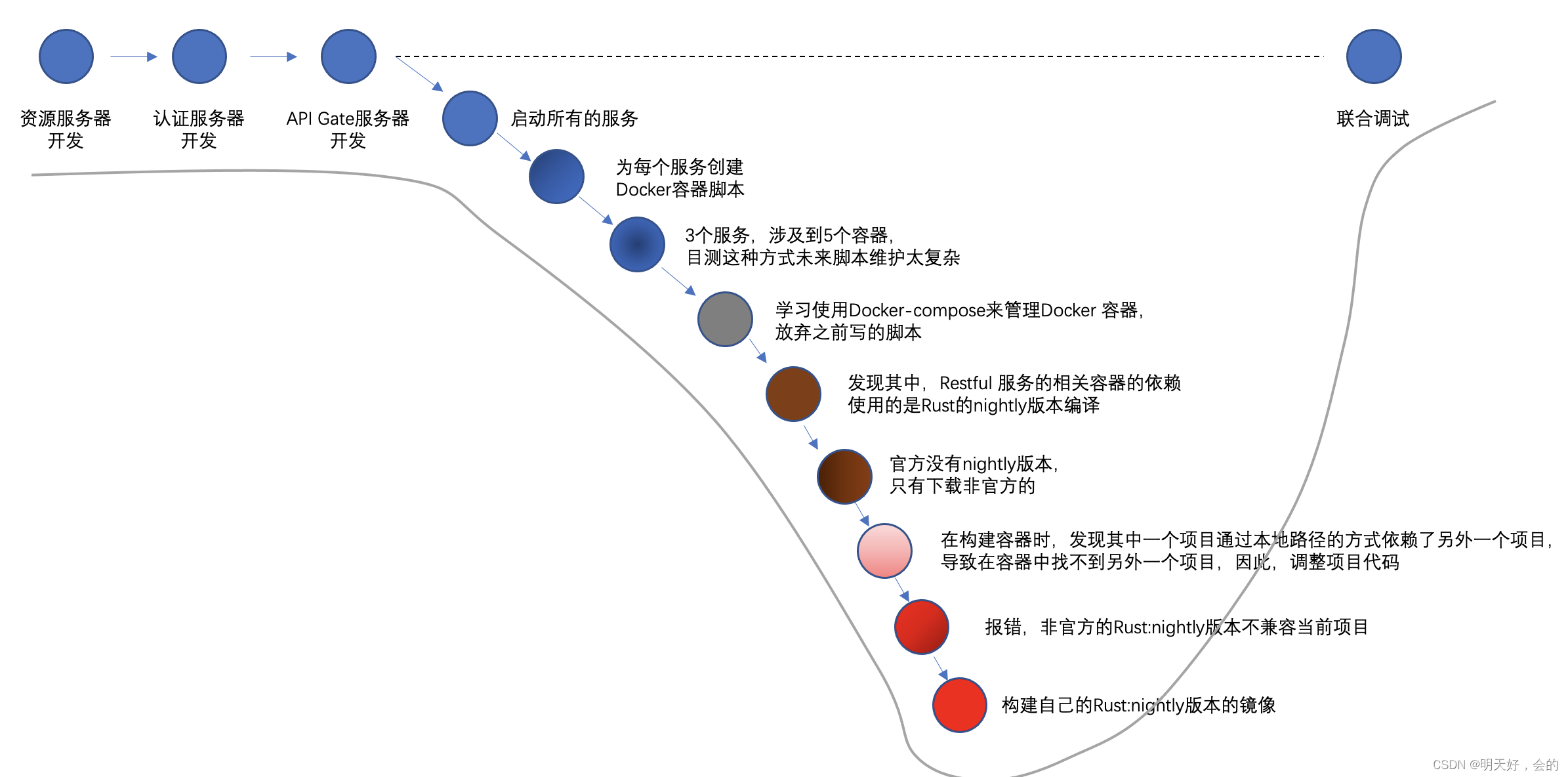
Rust-后端服务调试入坑记
这篇文章收录于Rust 实战专栏。这个专栏中的相关代码来自于我开发的笔记系统。它启动于是2023年的9月14日。相关技术栈目前包括:Rust,Javascript。关注我,我会通过这个项目的开发给大家带来相关实战技术的分享。 如果你关注过我的Rust 实战里…...

Flask四种配置方式
Flask是一个轻量级的Python Web框架,被广泛应用于Web开发中。Flask提供了多种配置方式,可以根据不同的需求和场景进行选择。本篇博客将介绍Flask的几种配置方式,并提供相关代码示例。 Flask应用程序的配置对象 在Flask中,应用程序…...
基于nodejs+vue备忘记账系统mysql
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
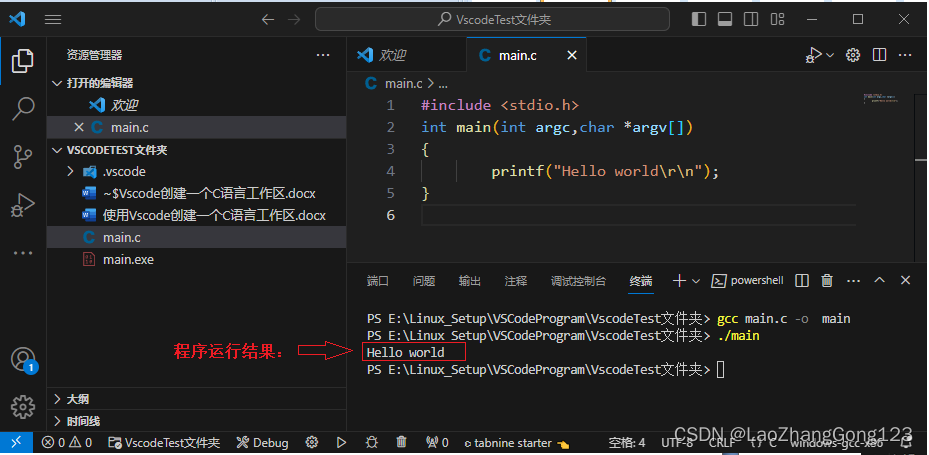
使用Vscode创建一个C_Hello程序
Vscode用来学习C语言语法确实很方便。问题是安装好了,不会用,或编译失败,也是常有的事情,其中一个原因就是不会创建工作区。下面介绍使用Vscode创建一个C语言工作区。有时候看着很简单,时间久了,我竟然忘记…...
【31】c++设计模式——>模板方法模式
模板方法模式通常由以下几个部分组成: 1.抽象基类(Abstract Base Class):抽象基类定义了一个算法的骨架,其中包含了模板方法和一些基本操作方法。模板方法在抽象基类中被声明为虚函数,它定义了算法的流程&…...
docker和K8S环境xxl-job定时任务不执行问题总结
文章目录 xxl-job 任务调度原理1 问题1 时区导致的任务没有执行的问题解决方案 2 执行器注册和下线导致的问题(IP问题)解决方案 3 问题3 调度成功,但是执行器的定时任务未执行4 问题4 数据库性能问题,导致查询任务和操作日志数据卡…...
)
【Leetcode】218.天际线问题(Hard)
一、题目 1、题目描述 城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。 每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] = [lefti, righti, heighti] 表示: l…...

try catch finally代码块的作用
try-catch-finally 代码块是用于处理程序中可能发生的异常情况的一种结构。它的作用在于: try 代码块中的代码用于包含可能会引发异常的代码。catch 代码块用于捕获并处理 try 代码块中抛出的异常。可以通过 catch 代码块中的逻辑来处理异常,如打印错误…...
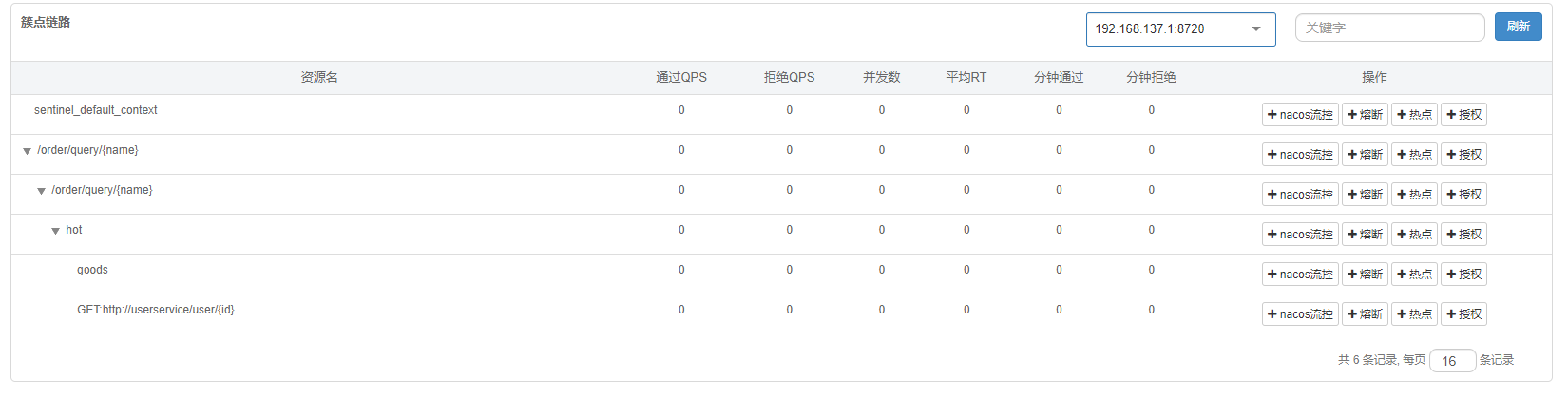
【Sentinel】Sentinel簇点链路的形成
说明 一切节点的跟是 machine-root,同一个资源在不同链路会创建多个DefaultNode,但是在全局只会创建一个 ClusterNode machine-root/\/ \EntranceNode1 EntranceNode2/ \/ \DefaultNode(nodeA) DefaultNode(nodeA)|…...

Elasticsearch之mapping
文章目录 以显式的方式创建一个映射查看某个具体索引的mapping定义向已存在的映射中添加一个新的属性查看映射中指定字段的定义信息更新已存在映射的某个字段 1、 官方文档地址 2、 字段类型 1、定义:映射是定义文档及其包含的字段如何存储和索引的过程。 2、每个…...

6、PostgreSQL 数据类型之一:数字类型和货币类型
PostgreSQL 作为一个强大的开源关系型数据库管理系统,本身支持多种数据类型,包括标准 SQL 数据类型以及一些扩展数据类型。 PostgreSQL 支持多种数据类型的设计理念是为了满足不同应用场景的需求,提供更大的灵活性和数据处理能力。原因如下&…...

计算机视觉与深度学习 | 基于点线融合的视觉惯性SLAM前端
===================================================== github:[https://github.com/MichaelBeechan] CSDN:[https://blog.csdn.net/u011344545] ===================================================== 引言 本文中将介绍视觉惯性SLAM的前端部分,首先是传感器数据处理…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...
