10_集成学习方法:随机森林、Boosting
文章目录
- 1 集成学习(Ensemble Learning)
- 1.1 集成学习
- 1.2 Why need Ensemble Learning?
- 1.3 Bagging方法
- 2 随机森林(Random Forest)
- 2.1 随机森林的优点
- 2.2 随机森林算法案例
- 2.3 随机森林的思考(--->提升学习)
- 3 随机森林(RF)的推广算法
- 3.1 Extra Tree
- 3.2 Totally Random Trees Embedding(TRTE)
- 3.3 Isolation Forest(IForest)
- 3.3.1 异常点的判断
- 3.4 RF随机森林总结
- 3.5 RF scikit-learn相关参数
- 4 Boosting(提升学习)
- 4.1 Adaboost算法
- 4.1.1 Adaboost算法原理
- 4.1.2 Adaboost算法
- 4.1.3 Adaboost算法推导
- 4.1.4 Adaboost算法构建过程
- 4.1.5 Adaboost算法的直观理解
- 4.1.6 Adaboost scikit-learn相关参数
- 4.1.7 Adaboost总结
- 4.2 梯度提升迭代决策树GBDT
- 4.2.1 GBDT算法原理
- 4.2.2 GBDT中回归算法和分类算法的区别
- 4.2.3 GBDT scikit-learn相关参数
- 4.2.4 GBDT总结
- 5 Bagging、Boosting的区别(面试重点)
- 6 Stacking
1 集成学习(Ensemble Learning)
1.1 集成学习
集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成单预测,因此优于任何一个单分类的做出预测。
- 集成学习的思想是将若干个学习器(分类器&回归器)组合之后产生一个新学习器。弱分类器(weak learner)指那些分类准确率只稍微好于随机猜测的分类器(error rate < 0.5);
- 集成算法的成功在于保证弱分类器的多样性(Diversity)。而且集成不稳定的算法也能够得到一个比较明显的性能提升。
- 常见的集成学习思想有:
- Bagging
- Boosting
- Stacking
1.2 Why need Ensemble Learning?
- 弱分类器间存在一定的差异性,这会导致分类的边界不同,也就是说可能存在错误。那么将多个弱分类器合并后,就可以得到更加合理的边界,减少整体的错误率,实现更好的效果;
- 对于数据集过大或者过小,可以分别进行划分和有放回的操作产生不同的数据子集,然后使用数据子集训练不同的分类器,最终再合并成为一个大的分类器;
- 如果数据的划分边界过于复杂,使用线性模型很难描述情况,那么可以训练多个模型,然后再进行模型的融合;
- 对于多个异构的特征集的时候,很难进行融合,那么可以考虑每个数据集构建一个分类模型,然后将多个模型融合。
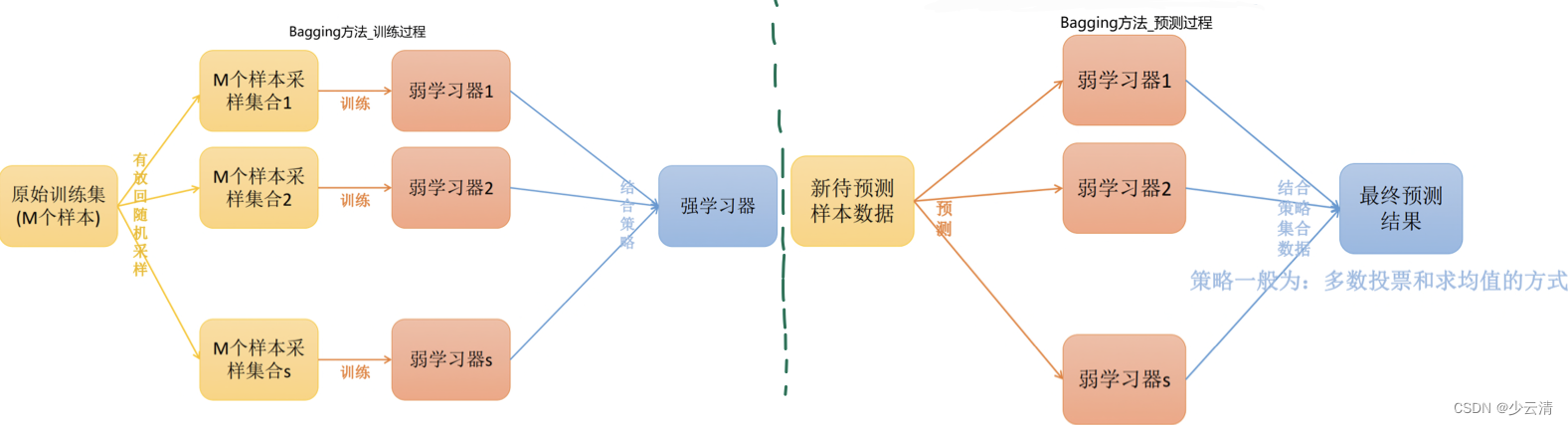
1.3 Bagging方法
- Bagging方法又叫做自举汇聚法(Bootstrap Aggregating),思想是:在原始数据集上通过有放回的抽样的方式,重新选择出S个新数据集来分别训练S个分类器的集成技术。也就是说这些模型的训练数据中允许存在重复数据。
- Bagging方法训练出来的模型在预测新样本分类的时候,会使用多数投票或者求均值的方式来统计最终的分类结果。
- Bagging方法的弱学习器可以是基本的算法模型,eg:Linear,Ridge,Lasso 、Logistic,Softmax,ID3,C4.5,CART,SVM、KNN等。
- 备注:Bagging方式是有放回的抽样,并且每个子集的样本数量必须和原始样本数量一致,但是子集中允许存在重复数据。
2 随机森林(Random Forest)
在Bagging策略的基础上进行修改后的一种算法:
- 从原始样本集(n个样本)中用Bootstrap采样(有放回重采样)选出n个样本;
- 从所有属性中随机选择K个属性,选择出最佳分割属性作为节点创建决策树;
- 重复以上两步m次,即建立m棵决策树;
- 这m个决策树形成随机森林,通过投票表决结果决定数据属于那一类
定义:在机器学习中,随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。
例如:如果你训练了5个树, 其中有4个树的结果是True, 1个数的结果是False, 那么最终结果会是True.
根据下列算法而建造每棵树:
-
用N来表示训练用例(样本)的个数,M表示特征数目。
-
输入特征数目m,用于确定决策树上一个节点的决策结果;其中m应远小于M。
-
从N个训练用例(样本)中以有放回抽样的方式,取样N次,形成一个训练集(即bootstrap取样),并用未抽到的用例(样本)作预测,评估其误差。
-
为什么要随机抽样训练集?
如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的
- 为什么要有放回地抽样?
如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是“有偏的”,都是绝对“片面的”(当然这样说可能不对),也就是说每棵树训练出来都是有很大的差异的;而随机森林最后分类取决于多棵树(弱分类器)的投票表决。

2.1 随机森林的优点
- 在当前所有算法中,具有极好的准确率
- 能够有效地运行在大数据集上
- 能够处理具有高维特征的输入样本,而且不需要降维
- 能够评估各个特征在分类问题上的重要性
- 对于缺省值问题也能够获得很好得结果
2.2 随机森林算法案例
- 使用随机森林算法API对乳腺癌数据进行分类操作,根据特征属性预测是否会得腺癌的四个目标属性的值,并理解随机森数量和决策树深度对模型的影响
- 数据来源:乳腺癌数据
# 目标属性
(bool)FInsemann arget vanabe
(bool)Schiller:target variable
(bool)Cytology:target variable
(bool)Biopsy:target variable
2.3 随机森林的思考(—>提升学习)
- 在随机森林的构建过程中,由于各棵树之间是没有关系的,相对独立的;在构建的过程中,构建第m棵子树的时候,不会考虑前面的m-1棵树。
- 思考:
- 如果在构建第m棵子树的时候,考虑到前m-1棵子树的结果,会不会对最终结果产生有益的影响?
- 各个决策树组成随机森林后,在形成最终结果的时候能不能给定一种既定的决策顺序呢?(也就是哪棵子树先进行决策、哪棵子树后进行决策)
3 随机森林(RF)的推广算法
RF算法在实际应用中具有比较好的特性,应用也比较广泛,主要应用在:分类、回归、特征转换、异常点检测等。常见的RF变种算法如下:
- Extra Tree
- Totally Random Trees Embedding(TRTE)
- Isolation Forest
3.1 Extra Tree
Extra Tree是RF的一个变种,原理基本和RF一样,区别如下:
- RF会随机采样来作为子决策树的训练集,而Extra Tree每个子决策树采用原始数据集训练;
- RF在选择划分特征点的时候会和传统决策树一样,会基于信息增益、信息增益率、基尼系数、均方差等原则来选择最优特征值;而Extra Tree会随机的选择一个特征值来划分决策树。
Extra Tree因为是随机选择特征值的划分点,这样会导致决策树的规模一般大于RF所生成的决策树。也就是说Extra Tree模型的方差相对于RF进一步减少。在某些情况下,Extra Tree的泛化能力比RF的强。
3.2 Totally Random Trees Embedding(TRTE)
-
TRTE是一种非监督的数据转化方式。将低维的数据集映射到高维,从而让映射到高维的数据更好的应用于分类回归模型。
-
TRTE算法的转换过程类似RF算法的方法,建立T个决策树来拟合数据。当决策树构建完成后,数据集里的每个数据在T个决策树中叶子节点的位置就定下来了,将位置信息转换为向量就完成了特征转换操作。

3.3 Isolation Forest(IForest)
- IForest是一种异常点检测算法,使用类似RF的方式来检测异常点;IForest算法和RF算法的区别在于:
- 在随机采样的过程中,一般只需要少量数据即可;
- 在进行决策树构建过程中,IForest算法会随机选择一个划分特征,并对划分特征随机选择一个划分阈值;
- IForest算法构建的决策树一般深度max_depth是比较小的。
- 区别原因:目的是异常点检测,所以只要能够区分异常的即可,不需要大量数据;另外在异常点检测的过程中,一般不需要太大规模的决策树。
3.3.1 异常点的判断
对于异常点的判断,则是将测试样本x拟合到T棵决策树上。计算在每棵树上该样本的叶子节点的深度ht(x)。从而计算出平均深度h(x);然后就可以使用下列公式计算样本点x的异常概率值,p(x,m)的取值范围为[0,1],越接近于1,则是异常点的概率越大。
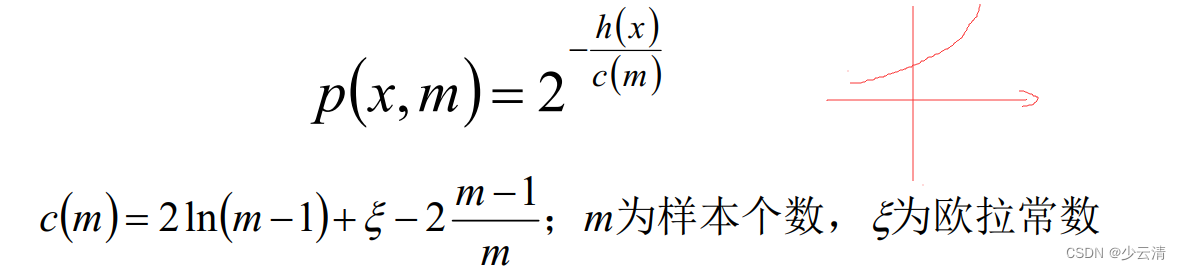
3.4 RF随机森林总结
RF的主要优点:
- 训练可以并行化,对于大规模样本的训练具有速度的优势;
- 由于进行随机选择决策树划分特征列表,这样在样本维度比较高的时候,仍然具有比较高的训练性能;
- 给以给出各个特征的重要性列表;
- 由于存在随机抽样,训练出来的模型方差小,泛化能力强;
- RF实现简单
- 对于部分特征的缺失不敏感。
RF的主要缺点:
- 在某些噪音比较大的特征上,RF模型容易陷入过拟合;
- 取值比较多的划分特征对RF的决策会产生更大的影响,从而有可能影响模型的效果。
3.5 RF scikit-learn相关参数
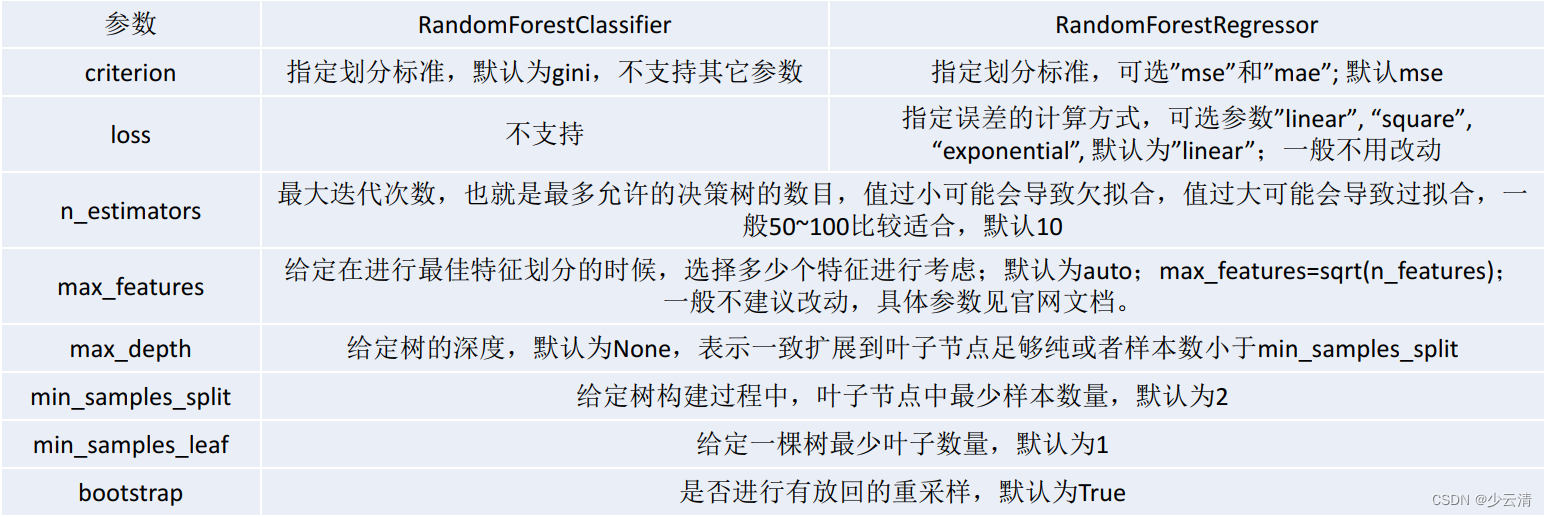
4 Boosting(提升学习)
-
提升学习(Boosting)是一种机器学习技术,可以用于回归和分类的问题,它每一步产生弱预测模型(如决策树),并加权累加到总模型中;如果每一步的弱预测模型的生成都是依据损失函数的梯度方式的,那么就称为梯度提升(Gradient boosting);
-
提升技术的意义:如果一个问题存在弱预测模型,那么可以通过提升技术的办法得到一个强预测模型;
-
常见的模型有:
- Adaboost
- Gradient Boosting(GBT/GBDT/GBRT)
4.1 Adaboost算法
4.1.1 Adaboost算法原理
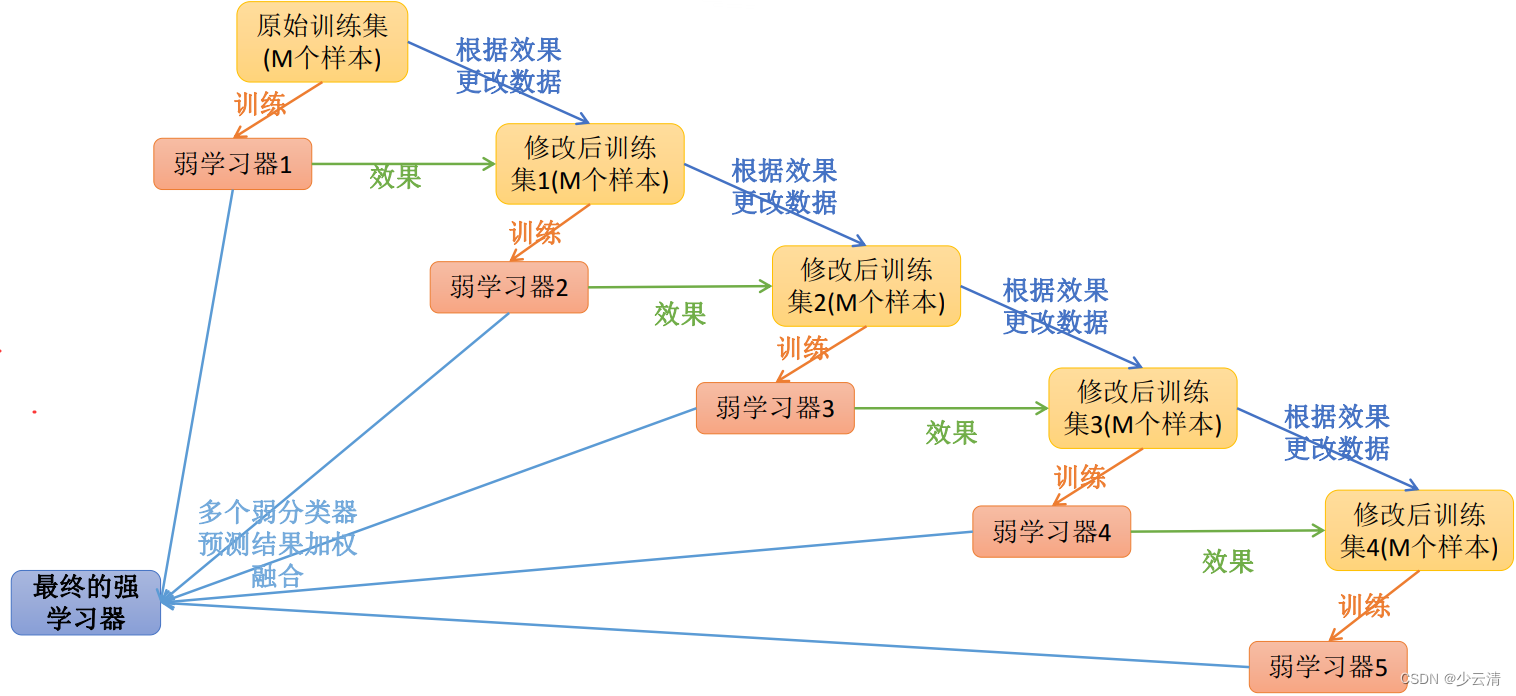
- Adaptive Boosting是一种迭代算法。每轮迭代中会在训练集上产生一个新的学习器,然后使用该学习器对所有样本进行预测,以评估每个样本的重要性(Informative)。换句话来讲就是,算法会为每个样本赋予一个权重,每次用训练好的学习器标注/预测各个样本,如果某个样本点被预测的越正确,则将其权重降低;否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就越大,也就是说越难区分的样本在训练过程中会变得越重要;
- 整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。
4.1.2 Adaboost算法
- Adaboost算法将基分类器的线性组合作为强分类器,同时给分类误差率较小的基本分类器以大的权值,给分类误差率较大的基分类器以小的权重值;构建的线性组合为 :

- 最终分类器是在线性组合的基础上进行Sign函数转换:
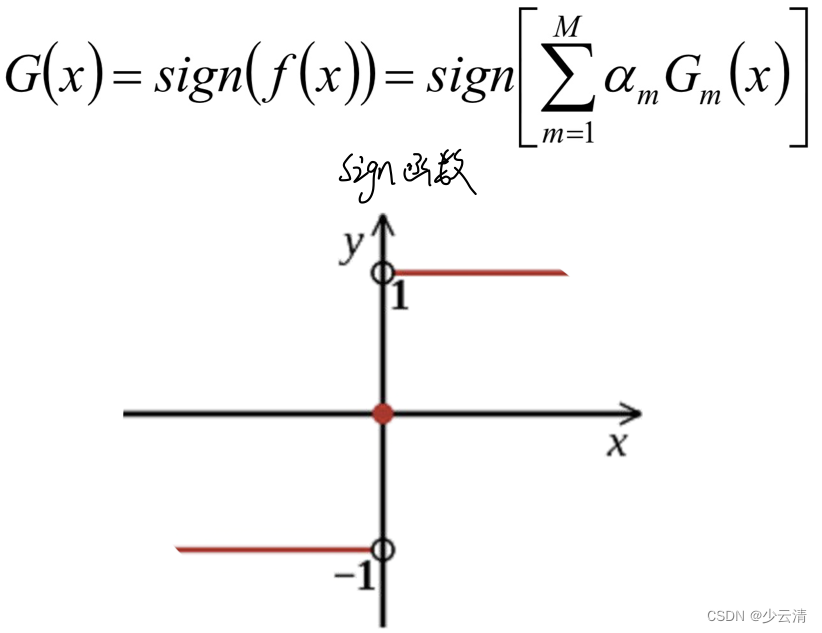
4.1.3 Adaboost算法推导


4.1.4 Adaboost算法构建过程

4.1.5 Adaboost算法的直观理解



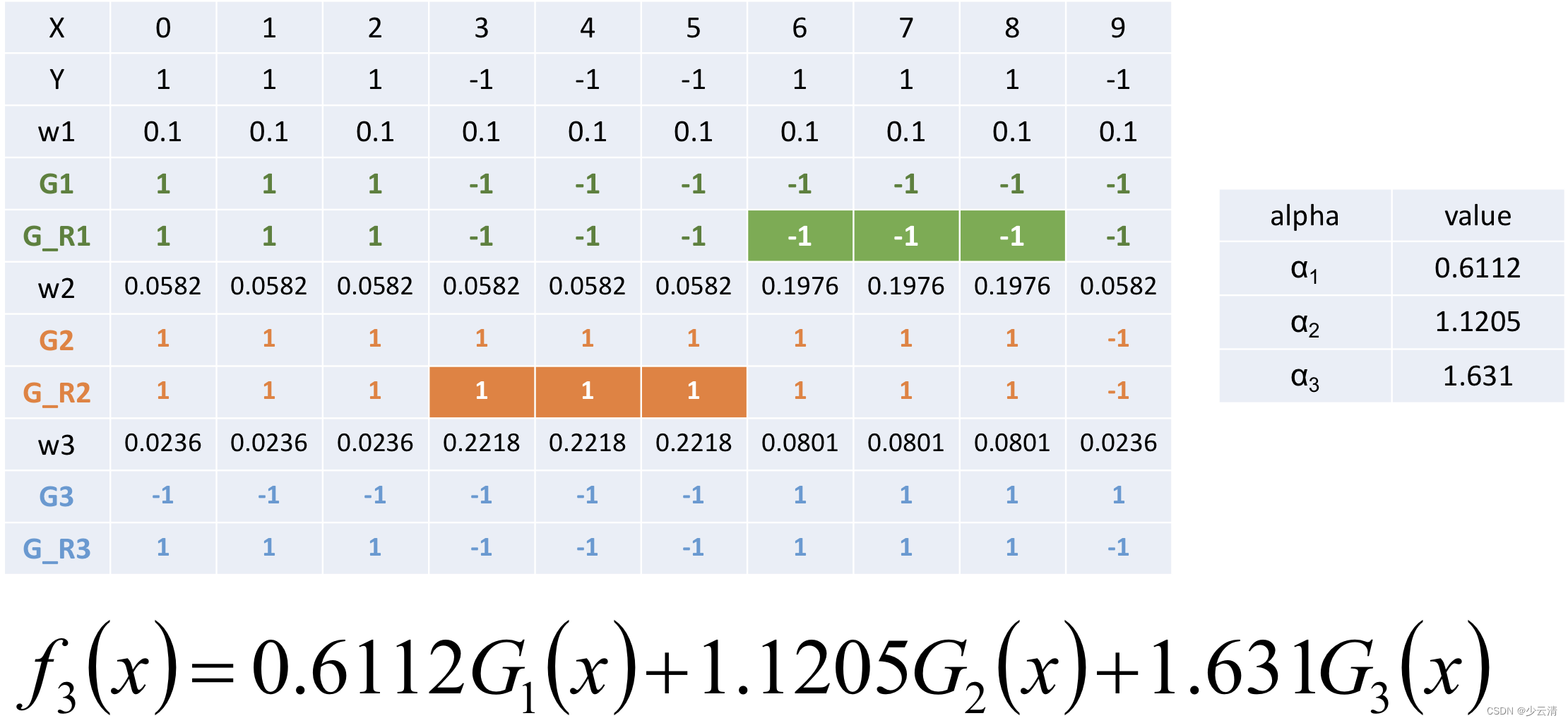
4.1.6 Adaboost scikit-learn相关参数
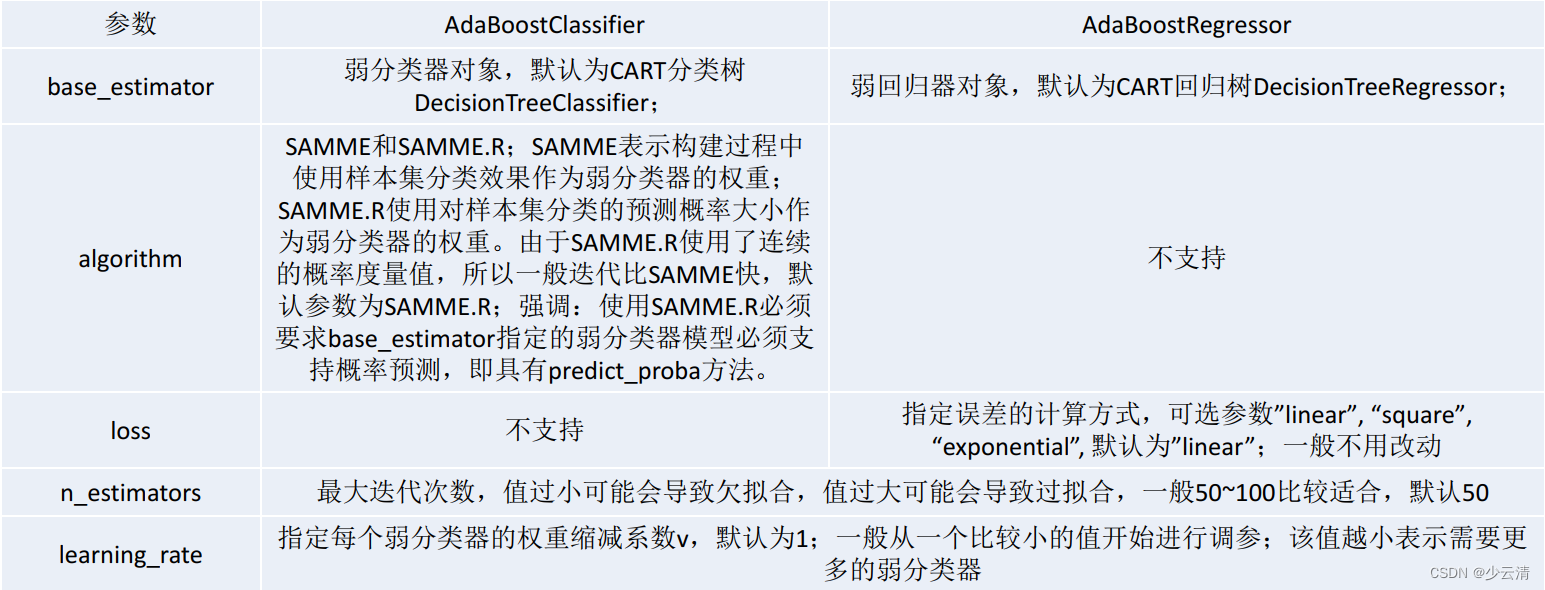

4.1.7 Adaboost总结
Adaboost的优点如下:
- 可以处理连续值和离散值;
- 模型的鲁棒性比较强;
- 解释强,结构简单。
Adaboost的缺点如下:
- 对异常样本敏感,异常样本可能会在迭代过程中获得较高的权重值,最终影响模型效果。
4.2 梯度提升迭代决策树GBDT
- GBDT也是Boosting算法的一种,但是和AdaBoost算法不同;区别如下:AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值,然后一轮一轮的迭代;GBDT也是迭代,但是GBDT要求弱学习器必须是CART模型,而且GBDT在模型训练的时候,是要求模型预测的样本损失尽可能的小。
- 别名:GBT(Gradient Boosting Tree)、GTB(Gradient Tree Boosting)、GBRT(Gradient Boosting Regression Tree)GBDT(Gradient Boosting Decison Tree)、MART(Multiple Additive Regression Tree)
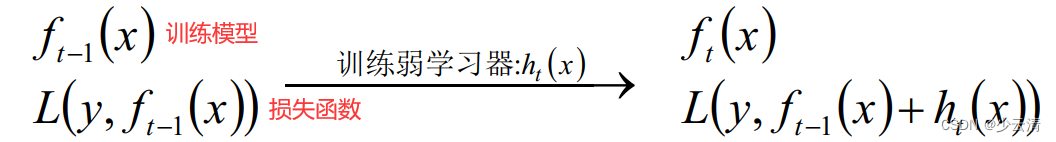
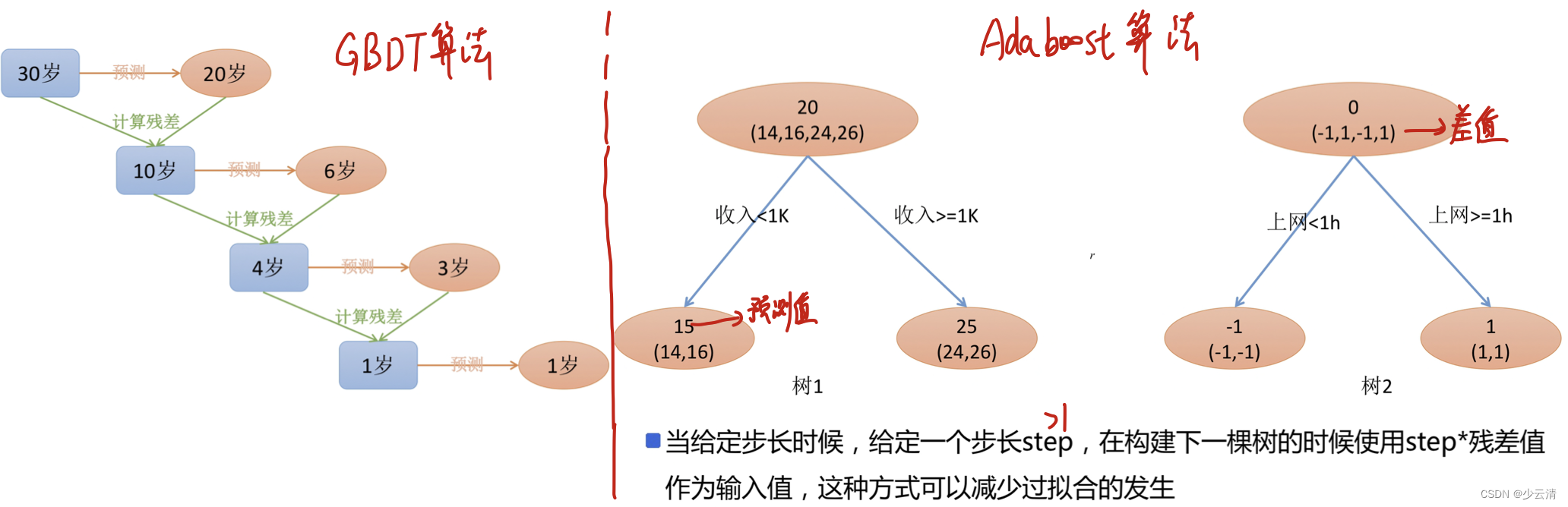
- GBDT由三部分构成:DT(Regression Decistion Tree),GB(Gradient Boosting)和Shrinkage(衰减)
- 由多棵决策树组成,所有树的结果累加起来就是最终结果
- 迭代决策树和随机森林的区别:
- 随机森林使用抽取不同的样本构建不同的子树,也就是说第m棵树的构建和前m-1棵树的结果是没有关系的
- 迭代决策树在构建子树的时候,使用之前子树构建结果后形成的残差作为输入数据构建下一个子树;然后最终预测的时候按照子树构建的顺序进行预测,并将预测结果相加。
4.2.1 GBDT算法原理

4.2.2 GBDT中回归算法和分类算法的区别
- 两者唯一的区别就是选择不同的损失函数
- 回归算法选择的损失函数一般是均方差(最小二乘)或者绝对值误差;而在分类算法中一般的损失函数选择对数函数来表示。
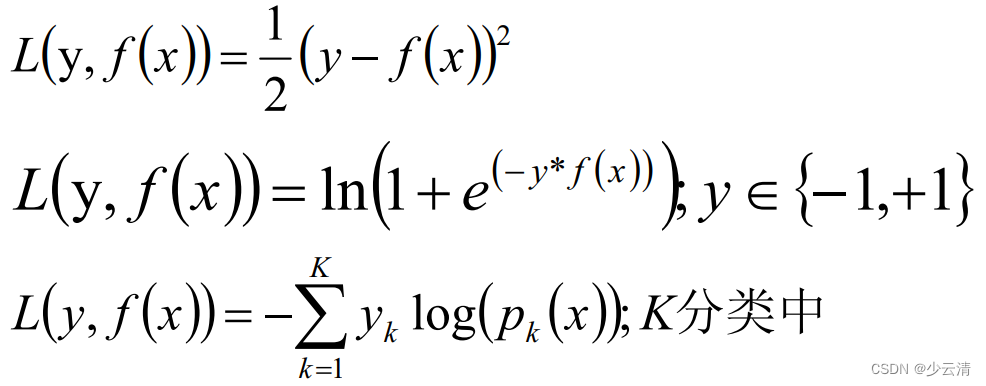
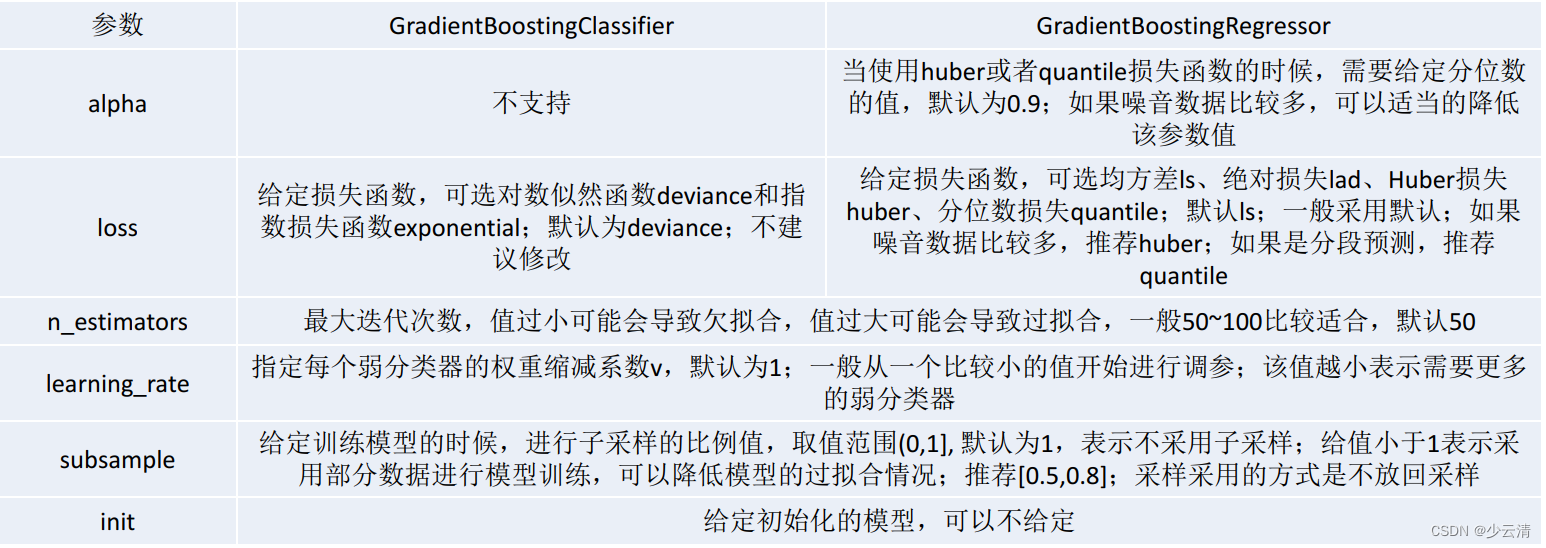
4.2.3 GBDT scikit-learn相关参数
4.2.4 GBDT总结
GBDT的优点如下:
- 可以处理连续值和离散值;
- 在相对少的调参情况下,模型的预测效果也会不错;
- 模型的鲁棒性比较强。
GBDT的缺点如下:
- 由于弱学习器之间存在关联关系(串行),难以并行训练模型。
5 Bagging、Boosting的区别(面试重点)
-
样本选择:Bagging算法是有放回的随机采样;Boosting算法是每一轮训练集不变,只是训练集中的每个样例在分类器中的权重发生变化,而权重根据上一轮的分类结果进行调整;
-
样例权重:Bagging使用随机抽样,样例的权重;Boosting根据错误率不断的调整样例的权重值,错误率越大则权重越大;
-
预测函数:Bagging所有预测模型的权重相等;Boosting算法对于误差小的分类器具有更大的权重。
-
并行计算:Bagging算法可以并行生成各个基模型;Boosting理论上只能顺序生产,因为后一个模型需要前一个模型的结果;
-
Bagging是减少模型的variance(方差);Boosting是减少模型的Bias(偏度)。
-
Bagging里每个分类模型都是强分类器,因为降低的是方差,方差过高是过拟合;Boosting里每个分类模型都是弱分类器,因为降低的是偏度,偏度过高是欠拟合。
error=Bias(偏度)+variance(方差)
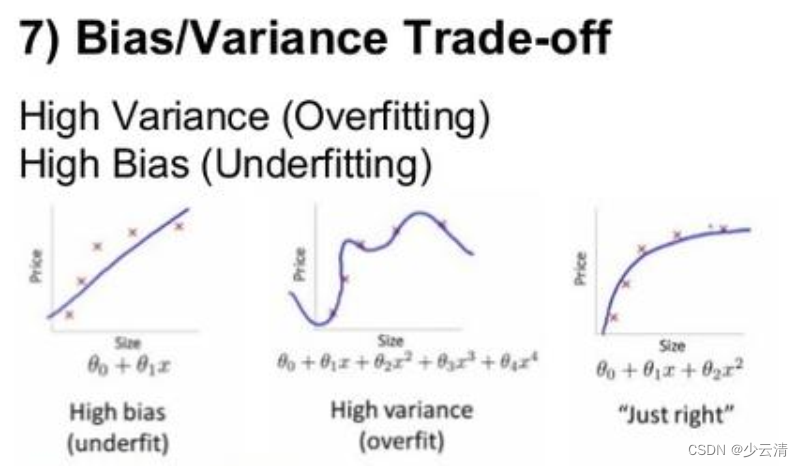
- Bagging对样本重采样,对每一轮的采样数据集都训练一个模型,最后取平均。由于样本集的相似性和使用的同种模型,因此各个模型的具有相似的bias和variance;
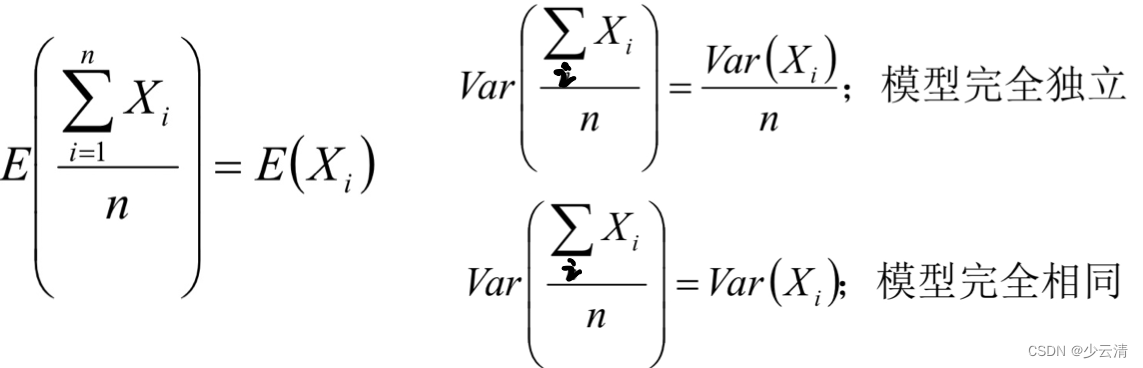
6 Stacking
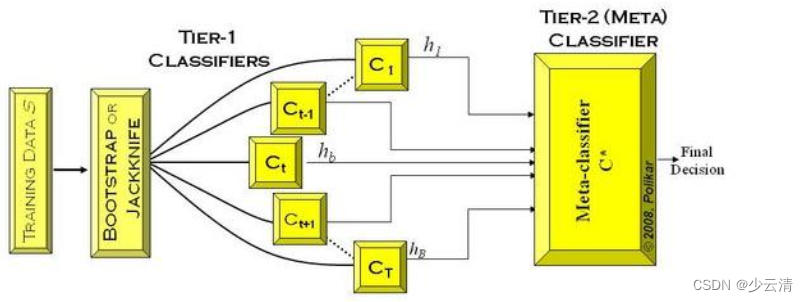
Stacking是指训练一个模型用于组合(combine)其它模型(基模型/基学习器)的技术。即首先训练出多个不同的模型,然后再以之前训练的各个模型的输出作为输入来新训练一个新的模型,从而得到一个最终的模型。一般情况下使用单层的Logistic回归作为组合模型。
相关文章:

10_集成学习方法:随机森林、Boosting
文章目录 1 集成学习(Ensemble Learning)1.1 集成学习1.2 Why need Ensemble Learning?1.3 Bagging方法 2 随机森林(Random Forest)2.1 随机森林的优点2.2 随机森林算法案例2.3 随机森林的思考(--->提升学习) 3 随机森林(RF&a…...

工业通信网关常用的工业通信协议
在工业领域中常常有不同的设备协同工作,而这些设备的通信协议和数据格式也有所差异,要想实现不同通信设备之间的数据传输互通,工业网关是一个重要的设备。 什么是工业网关 工业网关是一种能够连接多种不同设备并实现数据的收集、传输、处理和…...
如何将音频与视频分离
您一定经历过这样的情况:当你非常喜欢视频中的背景音乐时,希望将音频从视频中分离出来,以便你可以在音乐播放器中收听音乐。有没有一种有效的方法可以帮助您快速从视频中提取音频呢?当然是有的啦,在下面的文章中&#…...

【antd】form表单为空校验失效 form.item.rules传入非所需的api属性时,引起为空自动验证失效问题
现象 form表单的rules设置后,在form表单项为空时,不提醒required(正常现象),当开始输入后,马上触发了required为空校验,但此时表担心Input明明是有值的。 问题背景: form.item.ru…...

数据可视化的常见工具
Tableau: Tableau是一种流行的商业数据可视化工具,可以连接各种数据源,创建交互式仪表板和报告。它提供了强大的图表和图形功能。 Power BI: Power BI是微软的数据分析和可视化工具,与Microsoft生态系统紧密集成。它支持从多个数据源创建可视…...
不希望你的数据在云中?关闭iPhone或Mac上的iCloud
如果你不想使用iCloud,可以很容易地从设备设置中选择退出并关闭它。当你禁用iCloud时,它会删除该设备对iCloud的访问,但不会删除苹果服务器上的任何数据。我们将在本文末尾向你展示如何做到这一点。 注销iCloud并完全禁用它 如果你根本不…...
10 个最佳免费 PDF 压缩工具软件
PDF 是一种全球流行的文件格式,可在不损失质量或文本对齐的情况下传输文档。问题是许多文件共享应用程序和网站限制您可以共享或上传的 PDF 的大小。 10 个最佳免费 PDF 压缩工具软件 在这种情况下,您将需要一个可以为您减小 PDF 文件大小的应用程序。P…...
LVS+keepalived高可用集群
1、定义 keepalived为lvs应运而生的高可用服务。lvs的调度器无法做高可用,keepalived实现的是调度器的高可用,但keepalived不只为lvs集群服务的,也可以做其他代理服务器的高可用,比如nginxkeepalived也可实现高可用(重…...

虚拟化 vs. 裸金属:K8s 部署环境架构与特性对比
伴随着 IT 云化转型的逐步推进,越来越多的用户加入应用容器化改造的行列,并使用 Kubernetes(K8s)进行容器部署管理。然而,令不少用户感到困惑的是,由于大部分应用此前都部署在虚拟化或超融合环境࿰…...
C语言程序设计——题目:一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
题目:一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少? 程序分析: 假设该数为 x。 1、则:x 100 n2, x 100 168 m2 2、计算等式:m2 - n2…...
Python中使用cv2.resize()函数批量自定义缩放图像尺寸
目录 常用插值缩放方法缩放示例代码总结 常用插值缩放方法 cv2.resize()函数中的interpolation参数指定了图像缩放时使用的插值方法。以下是常用的插值方法: cv2.INTER_NEAREST:最近邻插值。该方法通过选择最接近目标像素的原始像素来进行插值。它是最…...
驱动开发5 阻塞IO实例、IO多路复用
1 阻塞IO 进程1 #include <stdlib.h> #include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <sys/ioctl.h> #include <fcntl.h> #include <unistd.h> #include <string.h>int main(int argc, char co…...

ElasticSearch:实现高效数据搜索与分析的利器!项目中如何应用落地,让我带你实操指南。
1.难点解答 收集到几个问题: elasticsearch是单独建一个项目,作为全文搜索使用,还是直接在项目中直接用? ES 服务器是要单独部署的,你可以把 ES 理解为 Redis。 新增数据时,插入到mysql中,需不…...
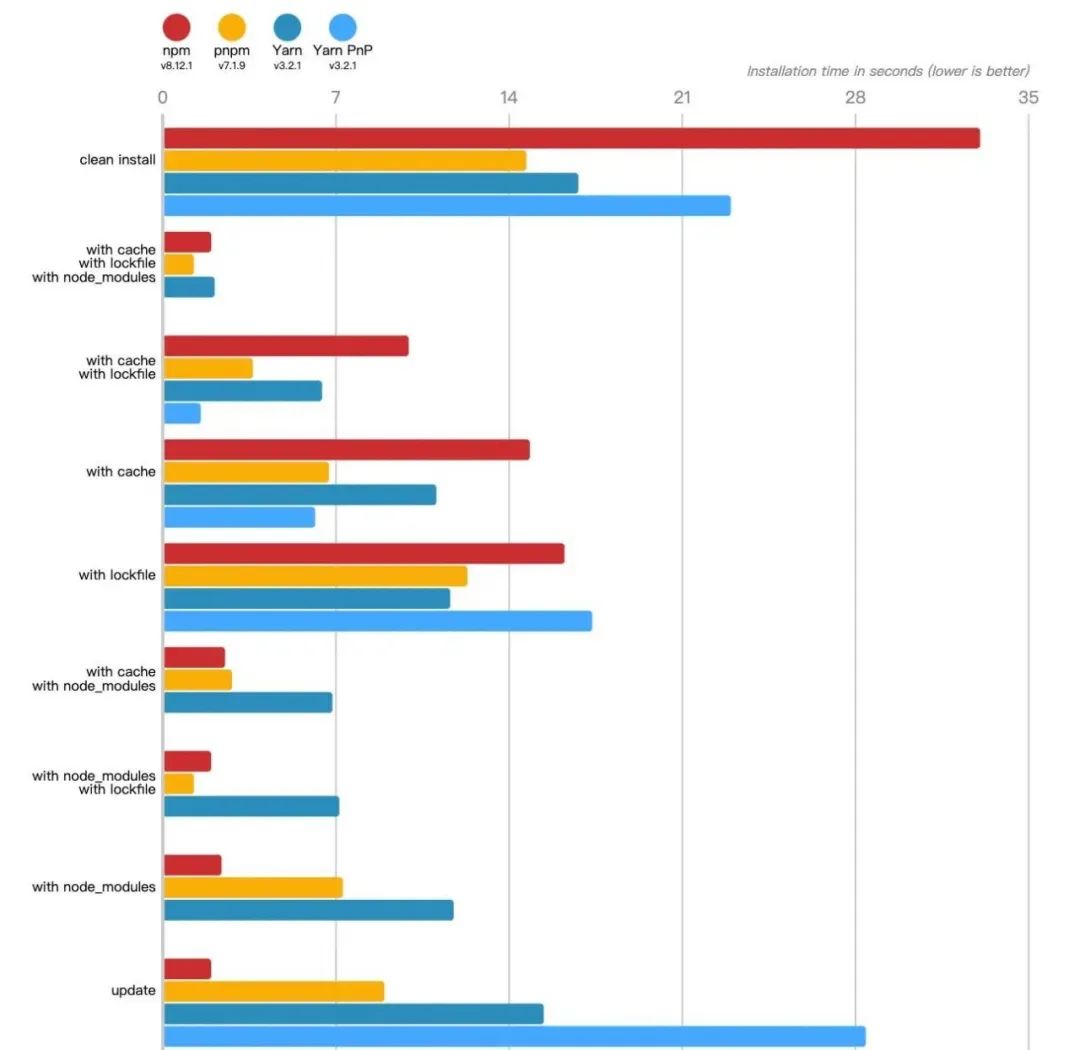
2023了,是时候使用pnpm了!
2023了,是时候使用pnpm了! Excerpt 2023了,是时候使用pnpm了! 什么是pnpm pnpm代表performant npm(高性能的npm),同npm和Yarn,都属于Javascript包管理安装工具,它较npm和…...
asp.net文档管理系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net文档管理系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语言开发 asp.net文档管理系统 二、功能介绍 (1…...

Parallels Client for Mac:改变您远程控制体验的革命性软件
在当今数字化的世界中,远程控制软件已经成为我们日常生活和工作中不可或缺的一部分。在众多远程控制软件中,Parallels Client for Mac以其独特的功能和出色的性能脱颖而出,让远程控制变得更加简单、高效和灵活。 Parallels Client for Mac是…...

Julia数组详解
文章目录 向量数列矩阵特殊数组数组函数 Julia系列:编程初步 向量 Julia中有两种向量,一种是类型统一的,另一种则可包含不同类型的变量,例如下面两个向量都是允许存在的 aNum [1,2,3] # 类型为 3-element Vector{Int64} aAny…...

用事务代码查看视图的函数
文章目录 1 Introduction2 Code 1 Introduction If we continue to see view with T-code. We can use the function for it . 2 Code REPORT z_websrv_con.CALL FUNCTION VIEW_MAINTENANCE_CALLEXPORTINGaction U "操作类型:U修改…...
--libcoap - coap数据处理)
LuatOS-SOC接口文档(air780E)--libcoap - coap数据处理
libcoap.new(code, uri, headers, payload) 创建一个coap数据包 参数 传入值类型 解释 int coap的code, 例如libcoap.GET/libcoap.POST/libcoap.PUT/libcoap.DELETE string 目标URI,必须填写, 不需要加上/开头 table 请求头,类似于http的headers,可选 string 请求体…...

js控制checkbox单选,获取checkbox的值,选中checkbox
声明:网上的资料杂七杂八的搞得我一个不熟悉前端的后端开发者弄起来贼难受,现在将实现了的做一个整合,希望能给你们带来点帮助(主要还是帮助我自己(●ˇ∀ˇ●),防止丢失) html代码组件示例 <div styl…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
