LeetCode 剑指 Offer 64. 求1+2+…+n
求 1+2+…+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
示例 1:
输入: n = 3
输出: 6
限制:
1 <= n <= 10000
解法一:利用逻辑运算符的短路:
class Solution {
public:int sumNums(int n) {n && (n += sumNums(n - 1));return n;}
};
此算法时间复杂度为O(n),空间复杂度为O(n)。
解法二:利用虚函数求解:
class base;
vector<base *> arr;class base {
public:virtual int plus(int i) {return 0;}
};class derived : public base {
public:virtual int plus(int i) override {return i + arr[!!i]->plus(i - 1);}
};class Solution {
public:int sumNums(int n) {arr.push_back(new base());arr.push_back(new derived());return arr[!!n]->plus(n);}
};
此算法时间复杂度为O(n),空间复杂度为O(n)。
解法三:纯C环境下没有虚函数,可以使用函数指针代替:
vector<int (*)(int)> funcArr;int sum(int i) {return i + funcArr[!!(i - 1)](i - 1);
}int sumTerminator(int i) {return i;
}class Solution {
public:Solution() {funcArr.push_back(sumTerminator);funcArr.push_back(sum);}int sumNums(int n) {return funcArr[!!n](n);}
};
此算法时间复杂度为O(n),空间复杂度为O(n)。
解法四:利用static成员:
class Solution {
public:Solution() {sum += i;++i;}int sumNums(int n) {i = 1;sum = 0;vector<Solution *> temp;for (int i = 0; i < n; ++i) {temp.push_back(new Solution);}return sum;}static int i;static int sum;
};int Solution::i = 1;
int Solution::sum = 0;
此算法时间复杂度为O(n),空间复杂度为O(n)。
解法五:利用模板,在编译期计算出结果,但这种方式需要输入是constexpr的:
class Solution {
public:template<int N> struct ans {enum {sum = N + ans<N - 1>::sum};};template<> struct ans<1> {enum {sum = 1};};int sumNums() {return ans<5>::sum; // 模板参数需要是constexpr的}
};
此算法时间复杂度为O(1),空间复杂度为O(1)。
解法六:将enum改为const static int,在较老的不支持类内const static的编译器上,常用enum代替const static,这种方法也需要模板参数是constexpr的:
class Solution {
public:template<int N> struct ans {const static int sum = N + ans<N-1>::sum;};template<> struct ans<1> {const static int sum = 1;};int sumNums() {return ans<3>::sum;}
};
此算法时间复杂度为O(1),空间复杂度为O(1)。
解法七:利用数组大小,根据求和公式sum = i(i+1)/2:
class Solution {
public:int sumNums(int i) {bool arr[i][i+1];return sizeof(arr) >> 1;}
};
此算法时间复杂度为O(n),空间复杂度为O(n)。
解法八:对于相乘的两个数A和B,将B转换为二进制,如果B中的第i位为1,这位1对结果的贡献为A * (1 << i),这个方法也被称作俄罗斯农民乘法,经常被用于两数相乘取模的场景,如果两数相乘已经超过数据范围,但取模后不会超过,我们就可以利用这个方法来拆位取模计算贡献,保证每次运算都在数据范围内。将其应用到求和公式:
class Solution {
public:int sumNums(int i) {int a = i, b = i + 1;int ans = 0;while (b) {if (b & 1) {ans += a;}b >>= 1;a <<= 1;}return ans >> 1;}
};
但是题目要求不能使用while循环,由于题目要求中对输入有限制,n最大为10000,因此最多循环14次,我们把循环中内容写14次即可:
class Solution {
public:int sumNums(int i) {int a = i, b = i + 1;int ans = 0;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;(b & 1) && (ans += a);b >>= 1;a <<= 1;return ans >> 1;}
};
此算法时间复杂度为O(lgn),空间复杂度为O(1)。
相关文章:

LeetCode 剑指 Offer 64. 求1+2+…+n
求 12…n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。 示例 1: 输入: n 3 输出: 6 限制: 1 < n < 10000 解法一:利用逻辑运算符的短路…...

Mapper代理开发
MyBatis快速开发https://blog.csdn.net/weixin_51882166/article/details/129204439?spm1001.2014.3001.5501 使用Mapper代理方式完成 定义与SQL映射文件同名的Mapper接口 ,将Mapper接口和SQL映射文件放置同一目录结构 新建接口和包: 将Mapper接口和…...

为什么在连接mysql时,设置 SetConnMaxIdleTime 没有作用
目录测试1go 1.15.15go 1.17.12测试2go 1.15.15go 1.17.12参考在使用golang 连接 mysql时,为了节省连接资源,在连接使用过后,希望在指定长度时间不再使用后,自动关闭连接。 这时,经常会使用SetConnMaxLifetime()&#…...

嵌入式开发利器
前言 俗话说,工欲善其事必先利其器,做嵌入式开发首先需要选择好的工具,对的工具,工具选对了能事半功倍,节省很多时间,那些开发大佬一般都会使用各种各样的工具,不同的环节使用不同的工具&#…...

Qt 的QString类的使用
Qt的QString类提供了很方便的对字符串操作的接口。 使某个字符填满字符串,也就是说字符串里的所有字符都有等长度的ch来代替。 QString::fill ( QChar ch, int size -1 ) 例: QString str "Berlin";str.fill(z);// str "zzzzzz"…...
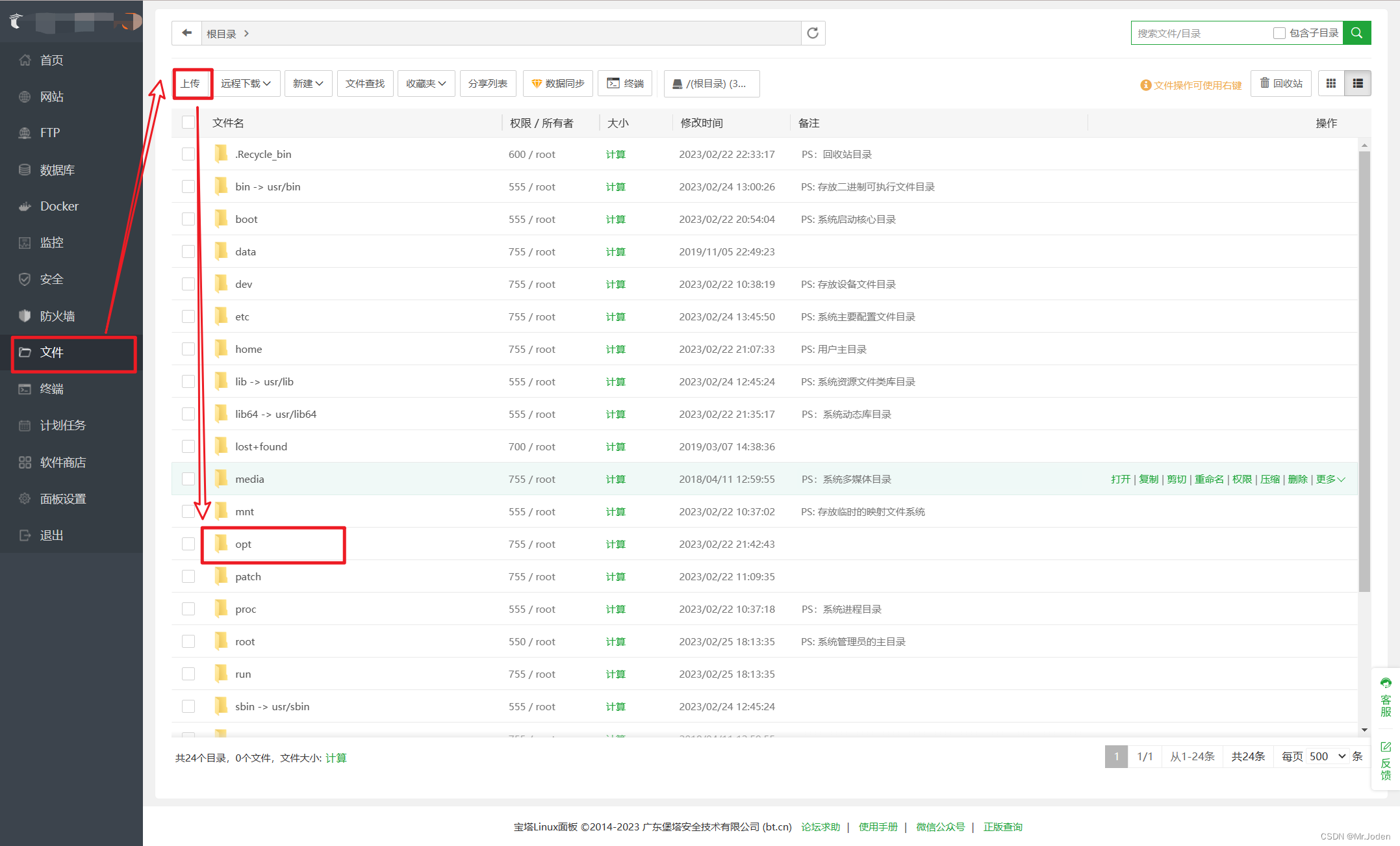
django项目部署(腾讯云服务器centos)
基本步骤: 购买腾讯云服务器并配配置好 >> 本地项目依赖收集准备 >> 上传项目等文件到服务器 >> 服务器安装部署软件和python环境 >> 开始部署(全局来看就这5个步骤) 目录 目录 1. 购买腾讯云服务器并配配置好 …...

计算机网络笔记、面试八股(一)——TCP/IP网络模型
Note:【计算机网络笔记、面试八股】系列文章共计5篇,现已更新3篇,剩余2篇(TCP连接、Web响应)会尽快更新,敬请期待! 本章目录1. TCP/IP网络模型1.1 应用层1.1.1 应用层作用1.1.2 应用层有哪些常用…...
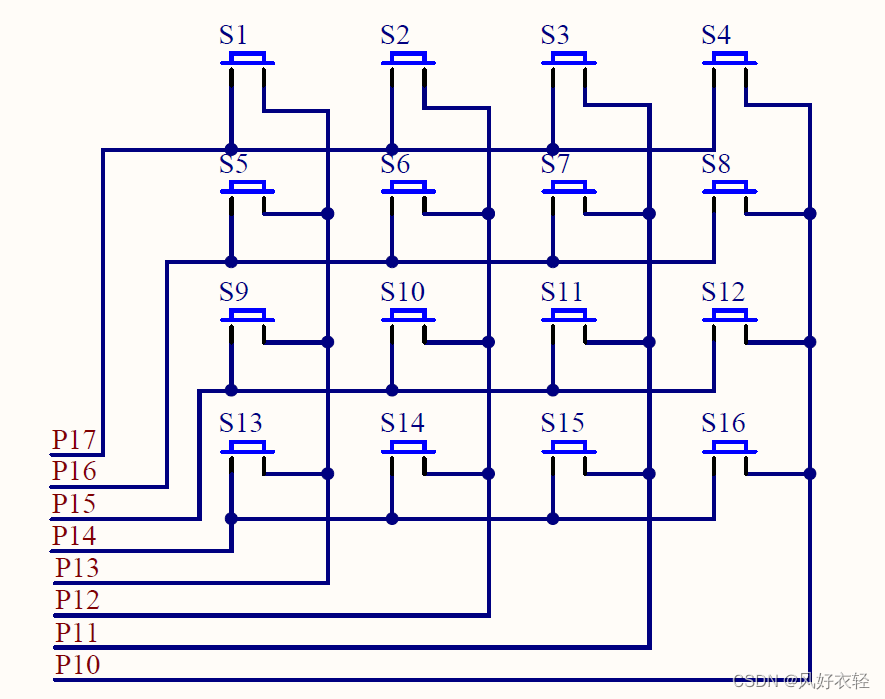
51单片机入门 - 简短的位运算实现扫描矩阵键盘
介绍 例程使用 SDCC 编译、 stcgal 烧录,如果你想要配置一样的环境,可以参考本专栏的第一篇文章“51单片机开发环境搭建 - VS Code 从编写到烧录”,我的设备是 Windows 10,使用普中51单片机开发板(STC89C52RC…...
Mr. Cappuccino的第45杯咖啡——Kubernetes之部署SpringBoot项目
Kubernetes之部署SpringBoot项目创建一个SpringBoot项目将SpringBoot项目打成Jar包使用Dockerfile制作镜像部署SpringBoot项目创建一个SpringBoot项目 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache…...

vscode在远程服务器提交git的时候无需每次都要输入账号密码的配置
要避免在每次 git 操作时都需要输入账号和密码,可以使用 SSH 鉴权,具体步骤如下:生成 SSH key在本地计算机上使用命令 ssh-keygen -t rsa -b 4096 生成 SSH key。这个命令将在 ~/.ssh 目录下生成两个文件:id_rsa 和 id_rsa.pub&am…...

【Spring 基础】
【Spring 基础】 一、 Spring 介绍 1. 简述 Spring 技术是 JavaEE 开发必备技能,企业开发技术选型专业角度 简化开发,降低企业级开发的复杂性 IoCAOP 事务处理 框架整合,高效整合其他技术,提高企业级应用开发与运行效率 MyBat…...

2023年全国最新机动车签字授权人精选真题及答案5
百分百题库提供机动车签字授权人考试试题、机动车签字授权人考试预测题、机动车签字授权人考试真题、机动车签字授权人证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 四、多选题 1.以下哪些气体属于排放污染物(…...

5138: 数字游戏
描述爸爸、妈妈还有YuYu一起玩一个数字游戏,玩家从某个数开始挨个轮流报数,当数字里含有4或7时,不能报出该数字,只能拍一下手。报数的顺序总是从YuYu开始,然后妈妈、爸爸,最后回到YuYu,以此类推…...

阅读笔记9——DenseNet
一、DenseNet DenseNet的网络结构如图1-1所示,其核心是Dense Block模块,Dense Block中的一个黑点就代表一个卷积模块(不是一个卷积层,而是DenseNet提出的一个BottleNeck模块,后文有讲解),每条黑…...
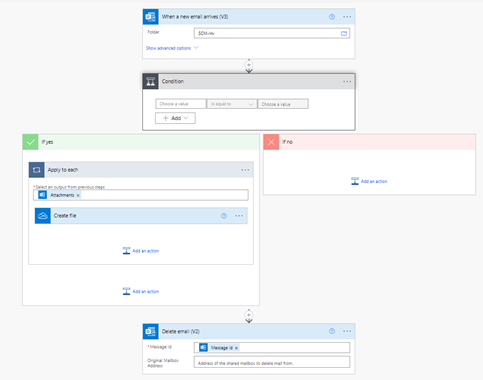
PowerAutomation获取邮件附件并删除这个邮件方法
这个文章是怎么来的呢?现在不是低代码开发平台启蒙阶段嘛?笔者也有幸在工作中进行了尝试,目前也已经在实际工作中结合Python进行了使用,当然,是可以提高IT的工作效率的。需求是这样的,想从公司的EBS平台报表…...

websocket报错集锦-不断更新中
问题1:Failed to construct ‘WebSocket’: An insecure WebSocket connection may not be initiated from a page loaded over HTTPS. 问题描述 Mixed Content: The page at https://AAAAAA.com was loaded over HTTPS, but attempted to connect to the insecur…...
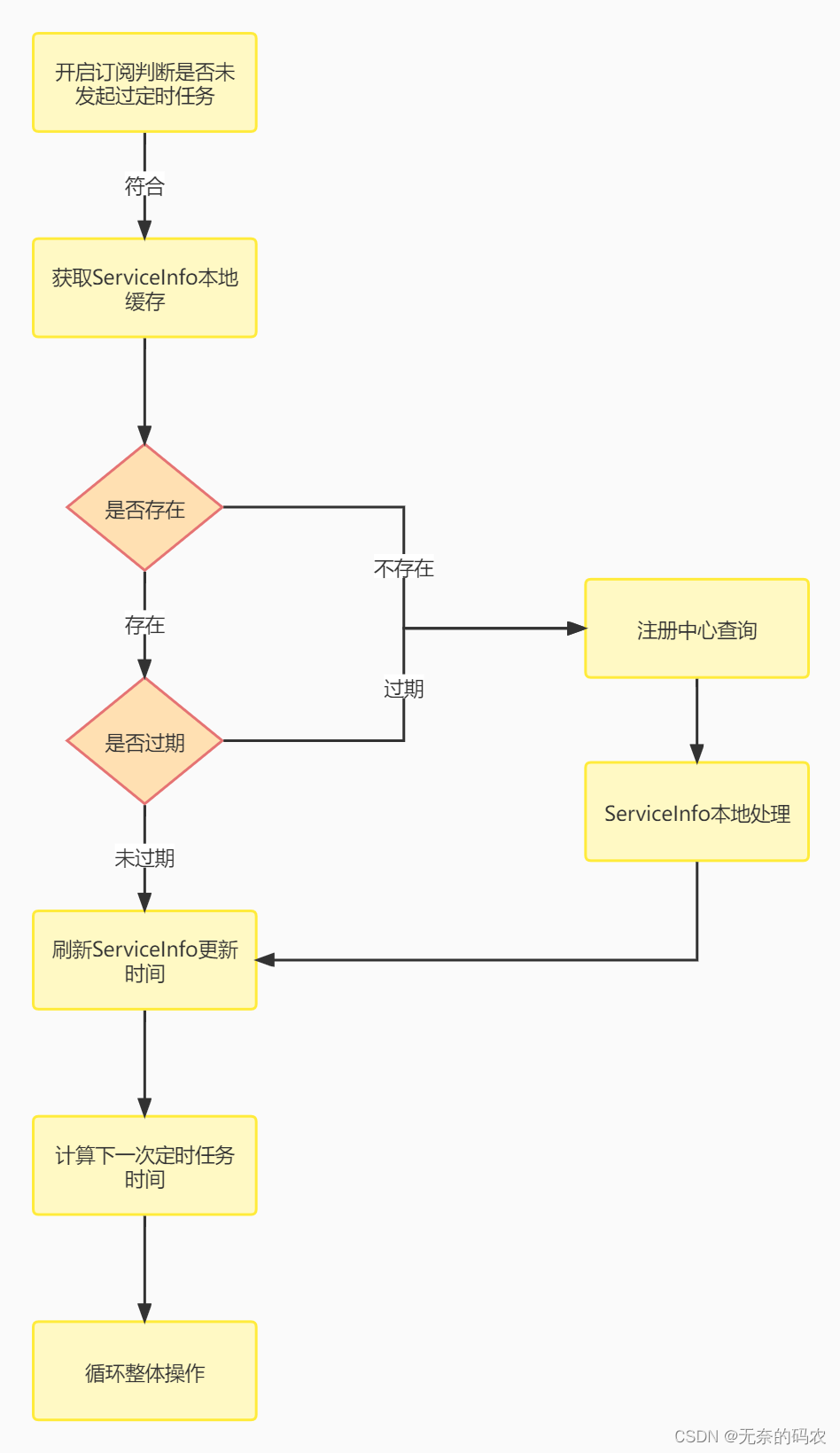
Spring Cloud Nacos源码讲解(七)- Nacos客户端服务订阅机制的核心流程
Nacos客户端服务订阅机制的核心流程 说起Nacos的服务订阅机制,大家会觉得比较难理解,那我们就来详细分析一下,那我们先从Nacos订阅的概述说起 Nacos订阅概述 Nacos的订阅机制,如果用一句话来描述就是:Nacos客…...

【华为OD机试模拟题】用 C++ 实现 - 对称美学(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 获得完美走位(2023.Q1) 文章目录 最近更新的博客使用说明对称美学题目输入输出示例一输入输出说明示例二输入输出说明备注Code使用说明 参加华为od机试,一定要注意不要完全背诵代码...
Go语言内存管理详解-学习笔记
1 自动内存管理 1.1 相关概念 Mutator:业务线程,分配新对象,修改对象指向关系Collector:GC线程,找到存活对象,回收死亡对象的内存空间Serial GC:只有一个collector(需要暂停&#…...
: Spatial weights)
Geospatial Data Science (4): Spatial weights
Geospatial Data Science (4): Spatial weights 在本节中,我们将学习空间分析中关键部分之一的来龙去脉:空间权重矩阵。这些是结构化的数字集,用于形式化数据集中观测值之间的地理关系。本质上,给定地理的空间权重矩阵是维度 N N N 乘以 N N N 的正定矩阵,其中...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
