一起学数据结构(10)——排序
从本文开始,通过若干篇文章展开对于数据结构中——排序的介绍。
1. 排序的概念:
将一堆杂乱无章的数据,通过一定的规律顺序排列起来。即将一个无序序列排列成一个有序序(由小到大或者由大到小)的运算。
在数据的排序中需要注意,如果需要排序的对象同时有多个数据域(例如对学生进行排序,往往有学号,班级等多个数据域),排序往往是针对于其中一个数据域进行的。
2. 排序的种类:
对于排序,本文及下面的文章中将着重介绍下列给出的排序:插入排序、希尔排序、选择排序、冒泡排序、快速排序、归并排序、计数排序。
3. 插入排序:
3.1 思路分析:
对于插入排序,其基本思想可以概括为:每一步都将待排序的对象,按照该对象与已有数据的大小关系,插入到前面已经排好序的一组数据的合适的位置中。因此,插入排序可以看作一个一边进行插入,一边保持已有序列有序的排序。
为了便于理解插入排序的基本思想,下面给出一个例子:

对于上面给出的例子,按照上面插入排序的基本思想来进行排序,则需要首先比较待插入元素与数组中已有元素进行比较。直到插入到一个合适的位置。所以对上述的案例进行排序后,最终结果为;
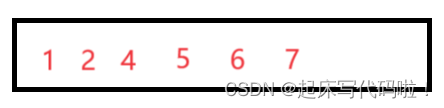
对于上面给出的插入排序的过程需要理解,并不是真的对数组不断插入新的元素进行排序。而是将数组中的一部分看作插入的部分,例如对于下面的数组:

将已经有序的序列,即数组中的称为有序序列。将后面的数组成的序列称之为无序序列。如果这个序列进行插入排序,只是将元素
看作待插入元素。通过不断比对待插入元素与数组中元素的大小关系,来调整元素
至合适的位置。
为了方便后续编写插入排序的代码,将有序序列的最后一位的下标记为,将待插入元素的下标记为
。所以,
一开始所对应的下标就是数组第一个元素的下标,即
,待插入元素的下标就是
,即数组中的第二个元素。对比调整后,数组中前两个元素会变为有序序列。接着按照上面的步骤循环,即令
,即有序序列的第二个元素,或者说数组中的第一个元素。待插入元素的下标等于
,即数组中的第二个元素。。。。。。。
3.2 代码演示:
通过上面给出的思路,可以总结出下面代码:
void InsertSort(int* a, int n)
{int end = 0;for (end = 0; end < n - 1; end++){int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];}else{break;}end--;}a[end + 1] = tmp;}}对于插入排序,因为没有开辟额外的空间,所以插入排序的空间复杂度为,当数组完全逆序时,插入排序需要执行的次数可以看作一个等差数列,所以插入排序的时间复杂度为
3.3 插入排序测试:
测试函数如下:
void TestInsertsort()
{int a[] = { 2,1,3,4,6,9,5,8 };int size = sizeof(a) / sizeof(int);InsertSort(a, size);ArrayPrint(a, size);
}其中函数是用于打印数组的函数,原理过于简单,不予解释,运行效果如下:
4. 希尔排序:
4.1 思路分析及代码演示:
对于上面给出的插入排序中提到,如果插入排序需要排序的数组是逆序的,则插入排序的时间复杂度为,如果需要排序的数组为顺序的,则时间复杂度为
,为了优化插入排序在排序逆序数组时较大的时间复杂度,可以尝试在对数组进行插入排序之间,先对数组进行依次预排序,让数组中某些元素是顺序的。对于先进行预处理,再进行一次插入排序的排序,就是文章本部分要介绍的希尔排序。例如下面的数组:

对于预排序,其步骤如下:首先确定一个间隔数,这里将这个间隔数命名为,通过利用
将数组分为若干个区间。并且对相邻区间的首元素进行一次类插入排序的操作。具体步骤将通过下面的图形进行演示:
1. 假设,则利用
分组后的数组可以表示为:

继续利用上面方法对数组中未分组的元素进行分组,可以表示为下面的图片,图中不同颜色的图形用于区分不同的组:
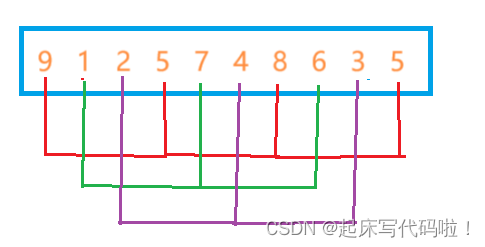
2. 接着,对于一组中的元素进行一次类插入排序的操作,即比较同一组的不同区间的首元素的大小关系,将小的元素放到前面。例如,对于红线组中的元素进行上述操作:

对于本部分的操作,可以利用插入排序的思想来实现,依旧定义表示本组第一个元素的下标,例如红线组的
,
则表示本组下一个区间的首元素的坐标,再创建一个变量
用于存储
所对应的元素。例如红线组的
。由于
所对应的元素>
所对应的元素。所以让
代表的元素覆盖到
的位置。再让
覆盖到
位置。该过程可用代码表示为:
void ShellSort(int* a, int n)
{int end = 0;int gab = 3;int tmp = a[end + gab];if (a[end] > tmp){a[end + gab] = a[end];}a[end] = tmp;
}但是,上面的过程并不完整,并且只能交换一次,加入遇到下面的情景:

假设 所对应的元素为
,
所对应的元素为
,按照上面的代码交换一次后:

可以看到,这两个元素的大小关系还是不满足。因此,并不能向上面仅仅对
,
的元素的大小关系进行判断,还需要对交换后前面的元素的关系重新进行一次判断,如果不满足则再次交换。方法为:再进行一次交换后,令
,此时
对应的元素为
,
对应的元素为
,对二者再次进行一次交换。
为了满足多次交换的目的需要利用到循环。所以对于循环的结束条件有两条:1是,2是元素的大小关系不符合。
即使在加上上面的补充后,代码也只能用于单个组中一组,
元素的交换,为了完成整租的交换,需要让
所对应的下标不断向后
个位置。所以可以将上述代码优化为:
//希尔排序
void ShellSort(int* a, int n)
{int gab = 3;for (int end = 0; end < n - gab; end += gab){int tmp = a[end + gab];while (end >= 0){if (a[end] > tmp){a[end + gab] = a[end];end -= gab;}else{break;}}a[end + gab] = tmp;}
}完善后的代码,可以一次性完成一组的预排序。但是在预排序的过程中需要对多组数据进行排序。通过对下面图形的观察可以得知,当初始值就为
时,此时进行预排序的就是紫色线条对应的组,也就是需要预排序的最后一组。所以,可以在将上面的代码进行一次优化,让其能够处理多组预排序
并且,对于的值也是变化的,
的值越大,数组中大的元素向后移动的距离越长,
越小,移动的距离也越小,当
,数组为有序。

代码如下:
//希尔排序
void ShellSort(int* a, int n)
{int gab = n;while (gab > 1){gab = gab / 2;for (int i = 0; i < gab; i++){for (int end = i; end < n - gab; end += gab){int tmp = a[end + gab];while (end >= 0){if (a[end] > tmp){a[end + gab] = a[end];end -= gab;}else{break;}}a[end + gab] = tmp;}}}
}对于预排序部分的代码,还有另一种更简洁的部分,这里先给出相应代码,再进行逻辑分析:
//希尔排序
void ShellSort1(int* a, int n)
{int gab = n;while (gab > 1){gab = gab / 2;for (int i = 0; i < n - gab; i++){int end = i;int tmp = a[end + gab];while (end >= 0){if (a[end] > tmp){a[end + gab] = a[end];end -= gab;}else{break;}}a[end + gab] = tmp;}}
}观察上面给出的代码,可以发现,相对于上面给出的预排序,这种预排序省略了一个循环。逻辑也不同。对于现在给出的预排序,并不是按照严格分组,先进行完一组,再进行一组。而是在确定了
之后,直接按照数组下标的顺序进行预排序,例如:

对于前面一种的预排序,是先对进行预排序,再对
进行预排序,再对
进行预排序,此时,红线所对应的组完成了预排序,于是再对绿线所对应的组的元素开始预排序,顺序为:
,
。
但是对于现在给出的预排序,预排序的顺序为:,
,
,
,。。。。。。
由于希尔排序的时间复杂度的计算极其复杂,这里直接给出结论,希尔排序的时间复杂度大致在左右。空间复杂度为
。
4.2 希尔排序测试:
测试函数如下:
void TestShellSort()
{int b[] = { 9,1,2,5,7,4,8,6,3,5 };int size = sizeof(b) / sizeof(int);ShellSort(b, size);printf("希尔排序:");ArrayPrint(b, size);
}结果如下:
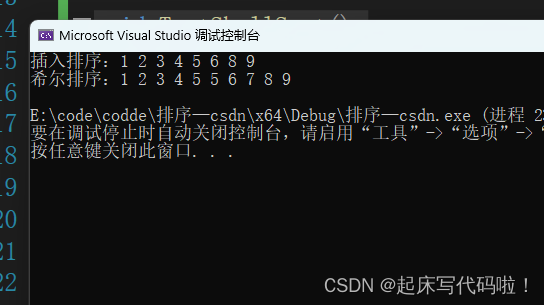
5. 冒泡排序:
5.1 代码演示:
对于冒泡排序的相关原理,可以在文章C语言——冒泡排序和qsort排序-CSDN博客浏览,文章在本部分只给出冒泡排序的相关代码以及测试结果,对实现原理不做论述。
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){int exchange = 0;for (int i = 1; i < n; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0){break;}}
}5.2 冒泡排序测试:
测试函数如下:
//冒泡排序void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){int exchange = 0;for (int i = 1; i < n; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0){break;}}
}void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}结果如下:

6. 堆排序 :
对于堆排序的相关原理及代码实现,在之前的文章如何利用堆来模拟堆排序-CSDN博客已经做了详细的解释,这里不再进行多余论述。
7. 选择排序:
7.1 思路分析以及代码演示:
对于选择排序的原理,总结下来只有一句话,即每次排序时,选出数组中最小的值以及最大的值,将最小的值换到数组的最左边,最大的值换到数组的最右边。
为了达成上述目的,可以创建两个变量,通过遍历数组将二者选择出来,再通过交换函数,让两个值在数组中的位置分别达到最左边,最右边。
代码如下:
void SelectSort(int* a, int n){int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);if (maxi == begin){maxi = mini;}Swap(&a[end], &a[maxi]);begin++;end--;}}7.2 选择排序测试:
测试函数如下:
TestSelectSort()
{int d[] = { 7,8,1,4,5,9,2,3,6};int size = sizeof(d) / sizeof(int);SelectSort(d, size);printf("选择排序:");ArrayPrint(d, size);
}结果如下:

对于选择排序,显而易见,时间复杂度为,空间复杂度为
。
相关文章:
一起学数据结构(10)——排序
从本文开始,通过若干篇文章展开对于数据结构中——排序的介绍。 1. 排序的概念: 将一堆杂乱无章的数据,通过一定的规律顺序排列起来。即将一个无序序列排列成一个有序序(由小到大或者由大到小)的运算。 在数据的排序中…...
php 数组基础/练习
数组 练习在最后 数组概述 概述与定义 数组中存储键值对 数组实际上是一个有序映射 key-value,可将其当成真正的数组、列表(向量)、散列表、字典、集合、栈、队列等 数组中的元素可以是任意类型的数据对象(可以嵌套数组&#…...
Redbook Chapter 7: Query Optimization翻译批注
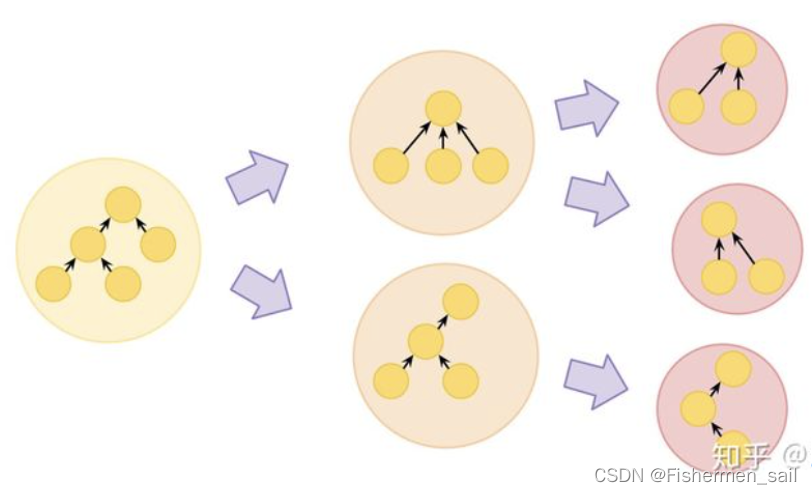
首先说明一下redbook上的几篇文章是做什么的。这几篇文章是通过几位作者对不同方面的论文进行阅读和筛选后,挑出其中具备代表性或者权威的论文来做分析,为读者提供阅读指导和建议,同时,也是对某个方面的论文进行高度的总结&#x…...
【分布式】大模型分布式训练入门与实践 - 04
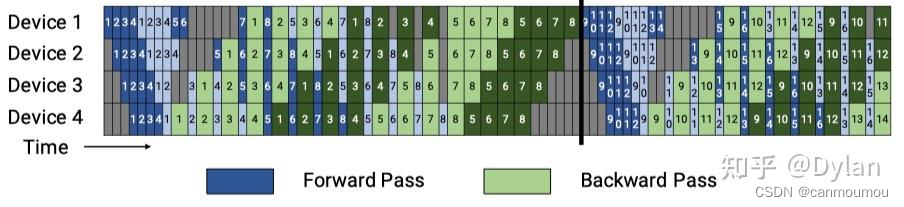
大模型分布式训练 数据并行-Distributed Data Parallel1.1 背景1.2 PyTorch DDP1) DDP训练流程2)DistributedSampler3)DataLoader: Parallelizing data loading4)Data-parallel(DP)5)DDP原理解析…...

欧拉图相关的生成与计数问题探究
最近学了一波国家集训队2018论文的最后一个专题。顺便带上了一些我的注解。 先放一波这个论文 1.基本概念 欧拉图问题是图论中的一类特殊的问题。在本文的介绍过程中,我们将会使用一些图 论术语。为了使本文叙述准确,本节将给出一些术语的定义。 定义…...
CSS3属性详解(一)文本 盒模型中的 box-ssize 属性 处理兼容性问题:私有前缀 边框 背景属性 渐变 前端开发入门笔记(七)
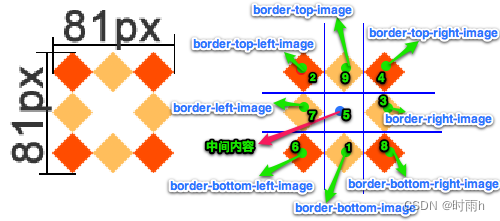
CSS3是用于为HTML文档添加样式和布局的最新版本的层叠样式表(Cascading Style Sheets)。下面是一些常用的CSS3属性及其详细解释: border-radius:设置元素的边框圆角的半径。可以使用四个值设置四个不同的圆角半径,也可…...

小程序:如何合理规划分包使主包不超过2M
背景 做过小程序项目的同学应该都有这样的经历,项目做着做着,突然发现代码包的大小超过了 2M,小程序无法提审,然后痛苦的删文件改代码来减少包大小。 虽然我们也知道小程序给我们提供了分包的功能可以减少主包的大小,…...

迭代器的封装与反向迭代器
一、反向迭代器 在list模拟实现的过程中,第一次接触了迭代器的封装,将list的指针封装成了一个新的类型,并且以迭代器的基本功能对其进行了运算符重载 反向迭代器是对正向迭代器的封装,并且体现了泛型编程的思想,任意…...

PHP项目学习笔记-萤火商城https://www.yiovo.com/doc
萤火商城学习笔记 注意事项关于建表增加页面流程前台页面的数据列表数据下拉列表的数据 关于时间的处理前台界面数据处理 多年没有碰过php代码了,这个项目不错,想好好学习下,持续更新 注意事项 打开APP_DEBUG有些时候改了前台页面后&#x…...

我国有多少个港口?
港口是什么? 港口是海洋运输中不可或缺的重要设施之一,是连接陆路和水路运输的重要节点。港口通常是指位于沿海地区的水陆交通枢纽,是船舶停靠、装卸货物、储存物资和维修船只的场所。港口一般由码头、泊位、仓库、货场、客运站等设施组成&a…...
uniapp实现登录组件之外区域置灰并引导登录
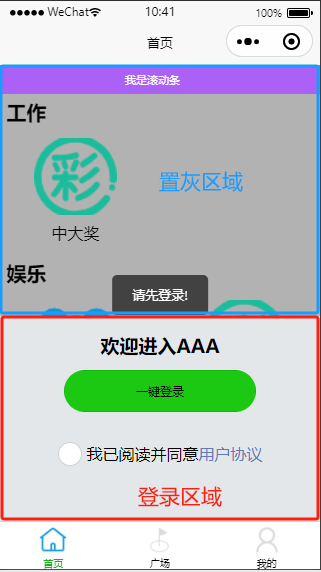
实现需求 每个页面需要根据用户是否登录决定是否显示登陆组件,登录组件半屏底部显示,登录组件之外区域置灰,功能按钮点击之后引导提示登录.页面效果如下: 实现思路说明 设置登录组件背景颜色为灰色,将页面分成登录区域(底部)和非登陆区域(上面灰色显示部分), 置灰区域添加…...
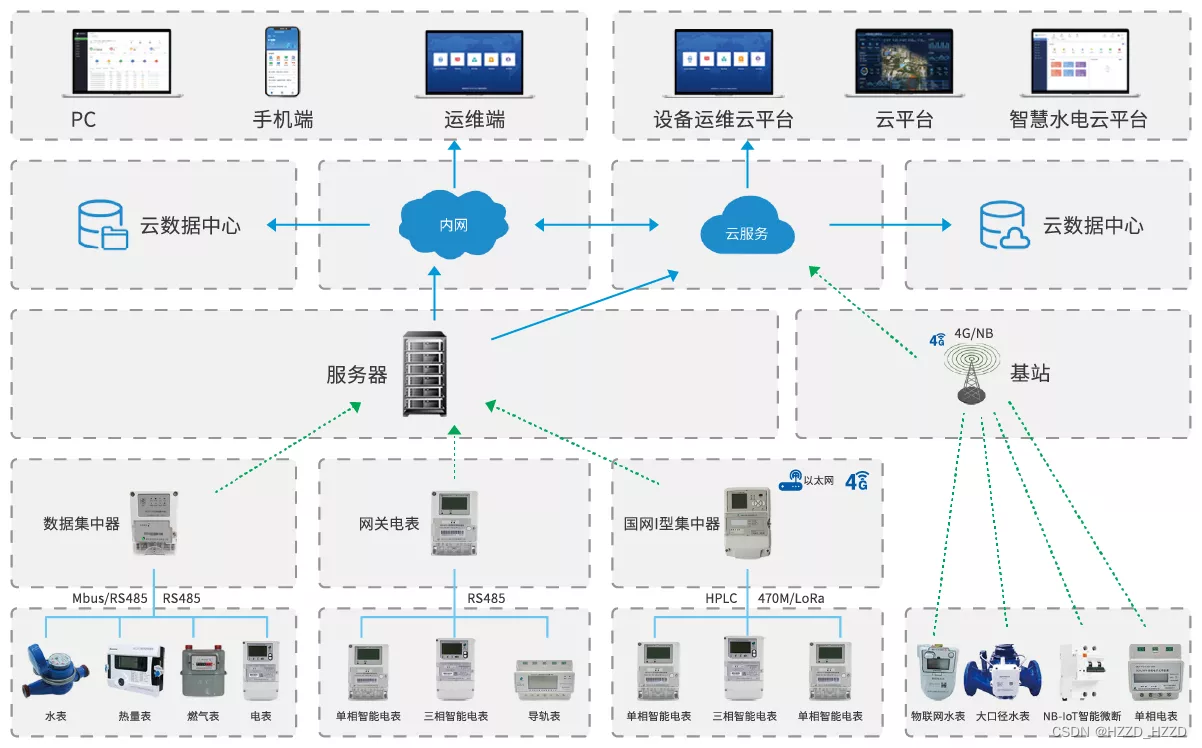
抄表系统是如何抄到电表水表的数据的?
抄表系统是一种利用无线通信技术,实现远程读取电表水表数据的系统。抄表系统主要由三部分组成:电表水表、集中器和后台管理平台。接下来,小编来为大家详细的介绍下抄表系统是如何抄到电表水表的数据的,一起来看下吧! 电表水表是抄…...
Qt之自定义事件QEvent
在Qt中,自定义事件的步骤大概如下: 1.创建自定义事件,自定义事件需要继承QEvent 2.使用QEvent::registerEventType()注册自定义事件类型,事件的类型需要在 QEvent::User 和 QEvent::MaxUser 范围之间,在QEvent::User之前是预留给系统的事件 3.使用sendEvent() 和 postEv…...

项目管理week5——交个作业
...

5.5G移动通信技术
5.5G即5G-Advanced,是一种移动通信技术。 5.5G 是 5G 和 6G 之间的过渡阶段,将在速率、时延、连接规模和能耗方面全面超越现有 5G,有望实现下行万兆和上行千兆的峰值速率、毫秒级时延和低成本千亿物联。按照国际标准组织 3GPP 定义ÿ…...

chrony时间服务
目录 1.1.重要性 1.2. Linux的两个时钟 1.3. NTP 1.4. Chrony介绍 2.安装与配置 2.1.安装: 2.2. Chrony配置文件分析 3.实验 3.1实验1 3.2实验2 3.常见时区 1.1.重要性 ●由于IT系统中,准确的计时非常重要,有很多种原因需要准确计时: 。在网络…...
音乐制作软件 Studio One 6 mac中文版软件特点
Studio One mac是一款专业的音乐制作软件,该软件提供了全面的音频编辑和混音功能,包括录制、编曲、合成、采样等多种工具,可用于制作各种类型的音乐,如流行音乐、电子音乐、摇滚乐等。 Studio One mac软件特点 1. 直观易用的界面&…...

SpringBoot整合redis集群和redis单节点
// 连接redis单节点配置类Configuration public class RedisConfig {Value("${spring.redis.host}")private String host;Value("${spring.redis.port}")private Integer port;Value("${spring.redis.password}")private String password;/*** d…...

【ARM Coresight 系列文章19.1 -- Cortex-A720 PMU 详细介绍】
文章目录 概述Cortex-A720 PMU Features1.1 PMU 使用介绍1.2 Performance monitors events1.3 Performance Monitors Extension registers1.3.1 Performance monitors program1.4 Performance monitors interrupts1.5 Interaction with the Performance Monitoring Unit and De…...
FoneDog iOS Unlocker(ios解锁工具) 适用macos电脑
FoneDog iOS Unlocker是一款专业的iOS设备解锁工具,旨在帮助用户解决iOS设备上的解锁问题。该软件支持解锁各种锁定类型,如数字密码锁、手势密码锁、Touch ID和Face ID等,可以解除iPhone、iPad和iPod Touch等设备的锁定状态。FoneDog iOS Unl…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

