SA+ST表维护height+单调队列维护:CF1073G
https://www.luogu.com.cn/problem/CF1073G
lcp相关的,先跑个sa,然后height建个ST表
现在考虑询问,我们按A和B按 r k rk rk 排序。现在考虑B->A,反过来同理。
我们可以用单调队列维护,满足height是单增的。因为越往前lcp必然越短。同时要维护有多少个。然后对于当前后缀的答案就是单调队列的大小了。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 400010
//#define M
//#define mo
struct node {int x, op;
};
struct Node {int x, k;
};
int n, m, i, j, k, T;
int tmp[N], bin[N], rk[N], sa[N], tot;
int f[N/2][22], Log2[N];
int h[N], height[N], c[2], ans, na, nb, q;
char s[N]; void psort() {memset(bin, 0, sizeof(bin)); int i; for(i=1; i<=n; ++i) bin[rk[i]]++; for(i=1; i<=max(n, 128ll); ++i) bin[i]+=bin[i-1]; for(i=n; i>=1; --i) sa[bin[rk[tmp[i]]]--]=tmp[i];
}int lcp(int i, int j) {if(i==j) return n-i+1; int l=rk[i]+1, r=rk[j]; int k=Log2[r-l+1]; return min(f[l][k], f[r-(1<<k)+1][k]);
}void SA() {for(i=1; i<=n; ++i) rk[i]=s[i], tmp[i]=i; psort();
// for(i=1; i<=n; ++i) printf("%lld ", sa[i]); printf("\n"); for(j=1; j<n; j<<=1) {for(i=n-j+1, k=0; i<=n; ++i) tmp[++k]=i; for(i=1; i<=n; ++i) if(sa[i]-j>0) tmp[++k]=sa[i]-j; psort(); tmp[sa[1]]=tot=1; for(i=2; i<=n; ++i) {if(rk[sa[i]]!=rk[sa[i-1]] || rk[sa[i]+j]!=rk[sa[i-1]+j]) ++tot; tmp[sa[i]]=tot; }memcpy(rk, tmp, sizeof(tmp)); }
// for(i=1; i<=n; ++i) printf("%d ", sa[i]); printf("\n"); for(i=1; i<=n; ++i) {h[i]=max(h[i-1]-1, 0ll); j = sa[rk[i]-1]; while(s[i+h[i]] == s[j+h[i]]) ++h[i]; }
// for(i=2; i<=n; ++i) printf("%d ", h[sa[i]]);
}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// T=read();
// while(T--) {
//
// }n=read(); q=read(); scanf("%s", s+1); SA(); for(i=2; i<=n; ++i) height[i]=f[i][0]=h[sa[i]]; for(k=1; k<=20; ++k) for(i=1, j=(1<<k-1)+1; i+(1<<k)-1<=n; ++i, ++j)f[i][k]=min(f[i][k-1], f[j][k-1]);for(i=2; i<=n; ++i) Log2[i]=Log2[i>>1]+1; while(q--) {na=read(); nb=read(); vector<node>v; for(i=1; i<=na; ++i) k=read(), v.pb({k, 0}); for(i=1; i<=nb; ++i) k=read(), v.pb({k, 1}); sort(v.begin(), v.end(), [] (node x, node y) { return rk[x.x]<rk[y.x]; }); stack<Node>z[2]; ans=c[0]=c[1]=0;
// z[v[0].op].push({n-v[0].x+1, 1});
// c[v[0].op]+=n-v[0].x+1; for(i=1; i<na+nb; ++i) {auto t=v[i-1]; int o = t.op, k=1, H=lcp(t.x, v[i].x); while(!z[o].empty() && z[o].top().x>=H) {auto t2 = z[o].top(); z[o].pop(); k+=t2.k, c[o]-=t2.x*t2.k; }z[o].push({H, k}); c[o]+=H*k; k=0; while(!z[o^1].empty() && z[o^1].top().x>=H) {auto t2 = z[o^1].top(); z[o^1].pop(); k+=t2.k, c[o^1]-=t2.x*t2.k; }if(k) z[o^1].push({H, k}), c[o^1]+=H*k; // printf("(%d %d) %lld %lld\n", t.x, t.op, H, c[v[i].op^1]); ans+=c[v[i].op^1]; }printf("%lld\n", ans); }return 0;
}相关文章:

SA+ST表维护height+单调队列维护:CF1073G
https://www.luogu.com.cn/problem/CF1073G lcp相关的,先跑个sa,然后height建个ST表 现在考虑询问,我们按A和B按 r k rk rk 排序。现在考虑B->A,反过来同理。 我们可以用单调队列维护,满足height是单增的。因为…...

Java中JVM、JRE和JDK三者有什么区别和联系?
任何语言或者软件的运行都需要环境。就像人要生活在空气中,鱼要活在水中,喜阴植物就不能放在阳光下暴晒一样,任何对象个体的存在都离不开其所需要的环境,编程语言亦是一样的。 java 语言的开发运行,也离不开 Java 语言…...
秋季期中考复现xj
flow analysis 1 What is the backdoor file name that comes with the server?( Including file suffix) 服务器自带的后门文件是什么?(含文件后缀) 题目还要求最后把那个文件名MD5一下,再去提交 开始的前三题是流量分析的&…...

【代码随想录】算法训练营 第十四天 第六章 二叉树 Part 1
递归遍历 递归法讲究的就是一个格式,在外边再定义一个用于递归求解的函数reverser,参数是递归的二叉树当前根节点和用于保存遍历得到的答案序列的vector容器; 函数中的格式就是,先写递归终止条件,也就是遍历的结点为…...
【访问控制】—>《熟练使用ACL进行上网行为管理》
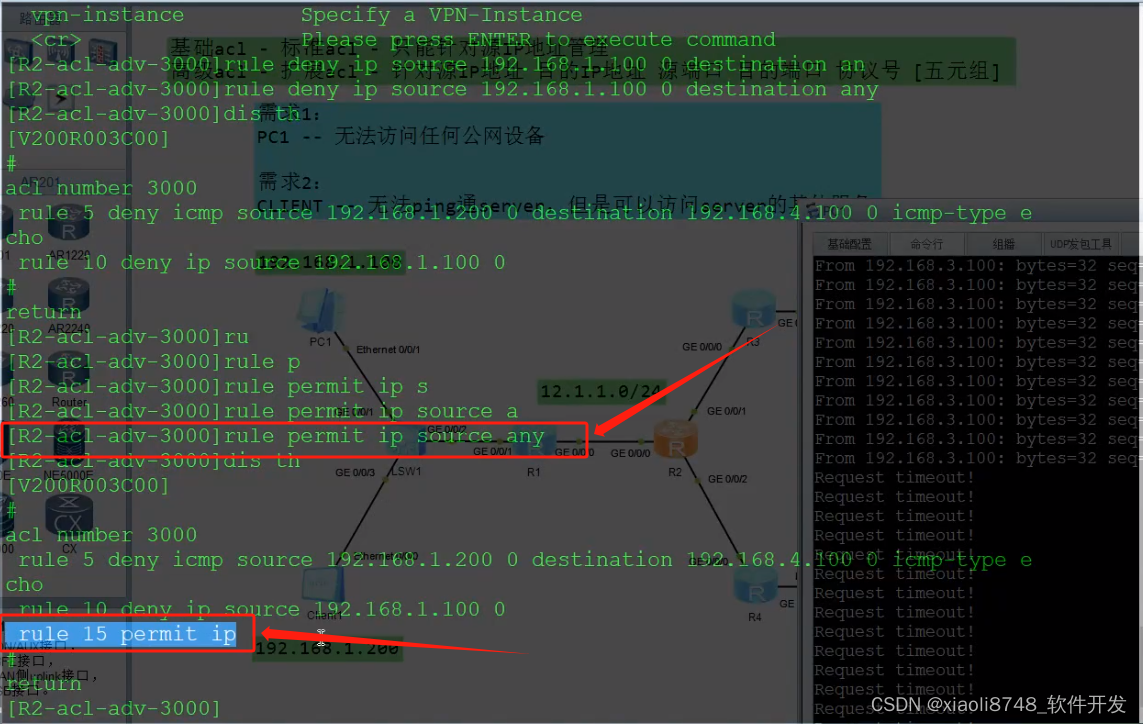
✍ 标准和高级ACL功能介绍; ✍ 思科和华为ACL功能有什么区别? ✍ 现网中ACL都有哪些使用场景? -- ACL - 访问控制列表 - 控制: 能通/不能通 -- ACL - 结合功能 list - 简化版本的行为管理 -- 插件性质的功能 --…...

MySQL外键,表与表的关系,多表查询,Navicat软件
外键 MySQL可以使用外键来保持表之间的关系完整性。 要设置外键,可以按照以下步骤进行操作: 在创建表时,使用FOREIGN KEY关键字来指定外键列: CREATE TABLE table1 (id INT PRIMARY KEY,name VARCHAR(50),table2_id INT,FOREI…...

Linux系统镜像备忘
阿里镜像源: ubuntu ubuntu-releases安装包下载_开源镜像站-阿里云 centos centos-stream安装包下载_开源镜像站-阿里云...

Docker容器端口在主机的映射
Docker容器端口在主机的映射 Docker 允许你在启动容器时进行多个端口映射,以便将容器内部的端口映射到宿主机上的不同端口。你可以使用-p或--publish标志来指定端口映射。以下是一些示例,说明如何在 Docker 启动容器时进行多个端口映射: 映…...
Spring Boot中RedisTemplate的使用
当前Spring Boot的版本为2.7.6,在使用RedisTemplate之前我们需要在pom.xml中引入下述依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId><vers…...

GSCoolink GSV6183 带嵌入式MCU的MIPI D-PHY 转 DP/eDP
Gscoolink GSV6183是一款高性能、低功耗的MIPI D-PHY到DisplayPort/eDP 1.4转换器。通过集成基于RISC-V的增强型微控制器,GSV6183创造了一种具有成本效益的解决方案,提供了上市时间优势。MIPI D-PHY接收器支持CSI-2版本1.3和DSI版本1.3,每条通…...

Linux文件系统 struct dentry 结构体解析
文章目录 前言一、目录项简介二、struct dentry2.1 简介2.2 dentry和inode关联2.3 目录项视图2.4 目录项状态2.5 目录项特点 三、dentry cache3.1 简介3.2 dentry cache 初始化3.3 dentry cache 查看 四、dentry与mount、file的关联五、其他参考资料 前言 这两篇文章介绍了: V…...

C++——vector
目录 vector vector常用接口 构造函数 operator[]size() 迭代器 范围for capacity() resize() reverse() push_back和pop_back insert erase() algorithm::sort 注意 迭代器失效 vector vector单词直译是向量的意思,这个容器可以容纳不同的类型数据&am…...

html5语义化标签
目录 前言 什么是语义化标签 常见的语义化标签 语义化的好处 前言 HTML5 的设计目的是为了在移动设备上支持多媒体。之前网页如果想嵌入视频音频,需要用到 flash ,但是苹果设备是不支持 flash 的,所以为了改变这一现状,html5 …...

SQL Server批量删除数据库中的表
如果想要删除数据库中temp 开头的中间表 1. SQL 语句实现 use [DBName] --todo go select drop table name from sys.tables where name like temp% go 将查询结果粘贴到数据库中运行 2. 数据库 单击目标数据库中的Tables ,然后按F7 键,按Name 进行排序&…...
使用SecScanC2构建P2P去中心化网络实现反溯源
个人博客: xzajyjs.cn 前言 这款工具是为了帮助安全研究人员在渗透测试过程中防止扫描被封禁、保护自己免溯源的一种新思路。其利用到了区块链中的p2p点对点去中心化技术构建以来构建代理池。 工具链接:https://github.com/xzajyjs/SecScanC2 实验过程 该工具分为…...

【API篇】七、Flink窗口
文章目录 1、窗口2、分类3、窗口API概览4、窗口分配器 在批处理统计中,可以等待一批数据都到齐后,统一处理。但是在无界流的实时处理统计中,是来一条就得处理一条,那么如何统计最近一段时间内的数据呢? ⇒ 窗口的概念&…...

软件测试面试1000问(含文档)
前前后后面试了有20多家的公司吧,最近抽空把当时的录音整理了下,然后给大家分享下 开头都是差不多,就让做一个自我介绍,这个不用再给大家普及了吧 同时,我也准备了一份软件测试视频教程(含接口、自动化、…...

进阶课4——随机森林
1.定义 随机森林是一种集成学习方法,它利用多棵树对样本进行训练并预测。 随机森林指的是利用多棵树对样本进行训练并预测的一种分类器,每棵树都由随机选择的一部分特征进行训练和构建。通过多棵树的集成,可以增加模型的多样性和泛化能力。…...
【Docker】Dockerfile使用技巧
开启Buildkit BuildKit是Docker官方社区推出的下一代镜像构建神器,可以更加快速,有效,安全地构建docker镜像。 尽管目前BuildKit不是Docker的默认构建工具,但是完全可以考虑将其作为Docker(v18.09)的首选…...
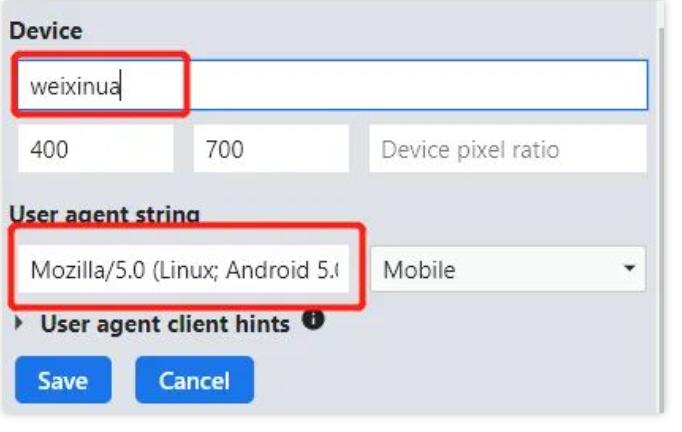
一招解决“请在微信客户端中打开链接”
一招解决“请在微信客户端中打开链接”-遇见你与你分享 在浏览器访问网站,却提示“请在微信客户端打开链接”。虽然这个情况你可能从未遇到过,但对于爱折腾的小伙伴,确是一道拦路虎 其实解决办法很简单,就是新建一个UA࿱…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
