PCA和LDA数据降维计算(含数学例子推导过程)
PCA算法和LDA算法可以用于对数据进行降维,例如可以把一个2维的数据降低维度到一维,本文通过举例子来对PCA算法和LDA算法的计算过程进行教学展示。
PCA算法计算过程(文字版,想看具体计算下面有例子)
1.将原始数据排列成n行m列的矩阵,n为数据的维度,m为数据的个数,即将每个数据竖着展示每个维度的值,然后将他们合成一个矩阵x
2.将x的每一行进行零均值化处理,即每一行的数据全部加起来,然后除以m,然后得到一个常数a,将这一行的每个数据都进行-a处理,其余的每一行以此类推。
3.求出协方差矩阵,c = X X X X T X^\mathrm T XT / m ;其中x和xt已经是进行零均值化处理过后的举证了
4.求出c的特征值以及对应的特征值向量,同时对特征向量进行单位化处理(一定要做,切记不能忘了)
5.特征向量按照特征值的大小从上到下按行排列成举证,取前k行组成矩阵p(k表示我们需要降低到的维度,例如如果我们要把数据降低到1维,我们取第一行就可以了)
6.Y =px,Y即为我们所求的的矩阵
LDA算法计算过程(文字版,想看具体计算下面有例子)
1.计算类内散度矩阵Sw
Sw求法,首先按照类别分别进行计算u,即1类计算u1,2类计算u2
u的计算方法为每行为每一类别的总和除以数量(即同类别的每一行全部加起来,除以个数),
然后Sw = Σ u \Sigma_u Σu Σ \Sigma Σ = Σ x 0 \Sigma_{x_0} Σx0(x-u0)(x-u0)T+ Σ x 1 \Sigma_{x_1} Σx1(x-u1)(x-u1)T,其中前面的x为u0类别里面的数据,x1为u1类别里面的数据,即各自处理各自的数据
2.计算类间散度矩阵Sb
Sb=(u0-u1)(u0-u1)T
3.求c = Sw-1Sb
4.计算c的特征值和特征向量,按特征值的大小把特征向量从左到右按列进行排序,取前k列组成矩阵p
5.Y=PT*X,Y即为我们所求的矩阵
例子:
我们给予两个种类的二维数据(拿竖线进行划分,左边的种类为1类,右边的种类为2类),求PCA和LDA将其进行降一维后的结果,即降低为一维数据
[ − 1 − 1 0 2 0 − 2 0 0 1 1 ] (例子) \left[ \begin{array}{ccc|cc} -1 & -1 & 0 & 2 &0\\ -2 & 0 & 0 & 1 &1 \end{array} \right] \tag{例子} [−1−2−10002101](例子)
PCA:
我们可以看到数据为2维5项数据,求出他的均值u0
u0第一行为(-1-1+0+2+0)/5= 0;
u0第二行为(-2 + 0 +0 + 1 +1)/5 = 0;
所以 u 0 = [ 0 0 ] (1) u_0=\left [ \begin{array}{c} 0\\ 0 \end{array} \right] \tag{1} u0=[00](1)
将五个数据分别减去u得到了新的X,因为这题比较特殊,经过0均值化处理后数据没有改变,所以x还是原来的数值没有发生改变
c = [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] ∗ [ − 1 − 2 − 1 0 0 0 2 1 0 1 ] / 5 = [ 6 / 5 4 / 5 4 / 5 6 / 5 ] c=\left [ \begin{array}{ccccc} -1 & -1 & 0 & 2 &0\\ -2 & 0 & 0 & 1 &1 \end{array} \right] * \left [ \begin{array}{cc} -1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1 \\ \end{array} \right] /5=\left [ \begin{array}{ccccc} 6/5 & 4/5 \\ 4/5 & 6/5 \\ \end{array} \right] c=[−1−2−10002101]∗ −1−1020−20011 /5=[6/54/54/56/5]
求出c的特征值和单位特征向量(这一步不会的可以移步考研数学李永乐,因为markdown写latex太难写了,题主就直接给出求得之后的答案了)
所求得的特征值为: λ 1 \lambda_1 λ1=2, λ 2 \lambda_2 λ2=2/5
然后我们求得对应的单位向量矩阵为(通过特征值的大小对特征向量进行按行排序)
p = 1 2 [ 1 1 − 1 1 ] p=\frac{1}{\sqrt[]{2}}\left [ \begin{array}{ccccc} 1 & 1 \\ -1 & 1 \end{array} \right] p=21[1−111]
因为我们要将数据从2维降低到1维,所以我们选择P的第一行数据进行降维度,p的第一行我们记作m,注意,此时的x为进行过0均值化后的数据
y = m ∗ x = 1 2 [ 1 1 ] ∗ [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] = 1 2 [ − 3 − 1 0 3 1 ] y=m*x=\frac{1}{\sqrt[]{2}}\left [ \begin{array}{ccccc} 1 & 1 \\ \end{array} \right]* \left [ \begin{array}{ccccc} -1& -1 &0 &2 &0 \\ -2 & 0 & 0 & 1& 1 \end{array} \right]=\frac{1}{\sqrt[]{2}}\left [ \begin{array}{ccccc} -3& -1 &0 &3 &1 \\ \end{array} \right] y=m∗x=21[11]∗[−1−2−10002101]=21[−3−1031]
我们所得到的y即为我们所求的结果
LDA:
[ − 1 − 1 0 2 0 − 2 0 0 1 1 ] (例子) \left[ \begin{array}{ccc|cc} -1 & -1 & 0 & 2 &0\\ -2 & 0 & 0 & 1 &1 \end{array} \right] \tag{例子} [−1−2−10002101](例子)
本题已知前三个数据为一个种类,后两个数据为一个种类
所以u0第一行为(-1-1+0)/3 = -2/3
u0第二行为(-2+0+0)/3 = -2/3;
u1第一行为(2+0)/2=1
u1第二行为(1+1)/2=1
所求得的u0u1如下所示:
u 0 = [ − 2 3 − 2 3 ] u 1 = [ 1 1 ] u_0=\left [ \begin{array}{ccccc} -\frac{2}{3}\\ -\frac{2}{3} \end{array} \right] u_1=\left [ \begin{array}{ccccc} {1}\\ {1}\\ \end{array} \right] u0=[−32−32]u1=[11]
然后我们选择套公式进行Sw的计算,将前三个值带入到前面的x0中,后面的两个值带入到后面的x1中,求得的Sw。
Sw = Σ u \Sigma_u Σu Σ \Sigma Σ = Σ x 0 \Sigma_{x_0} Σx0(x-u0)(x-u0)T+ Σ x 1 \Sigma_{x_1} Σx1(x-u1)(x-u1)T
Sw的结果为:
S w = [ 2 3 2 3 2 3 8 3 ] + [ 2 0 0 0 ] = [ 8 3 2 3 2 3 8 3 ] S_w=\left [ \begin{array}{ccccc} \frac{2}{3} & \frac{2}{3}\\ \frac{2}{3} & \frac{8}{3} \\ \end{array} \right]+\left[ \begin{array}{ccccc} 2& 0\\ 0 & 0 \\ \end{array} \right] =\left[ \begin{array}{ccccc} \frac{8}{3} & \frac{2}{3}\\ \frac{2}{3} & \frac{8}{3} \\ \end{array} \right] Sw=[32323238]+[2000]=[38323238]
然后我们求出Sw-1,求逆矩阵的方法也可以参照考研数学,求出来之后的值为:
S w − 1 = [ 2 5 − 1 10 − 1 10 2 5 ] S_w^{-1}=\left [ \begin{array}{ccccc} \frac{2}{5} & -\frac{1}{10}\\ -\frac{1}{10} & \frac{2}{5} \\ \end{array} \right] Sw−1=[52−101−10152]
计算类间散度矩阵Sb
Sb=(u0-u1)(u0-u1)T
求出Sb的值为:
S b = [ 25 9 25 9 25 9 25 9 ] S_b=\left [ \begin{array}{ccccc} \frac{25}{9} & \frac{25}{9}\\ \frac{25}{9} & \frac{25}{9} \\ \end{array} \right] Sb=[925925925925]
然后我们计算c=Sw-1*Sb。
求得c为:
c = [ 6 5 6 5 6 5 6 5 ] c=\left [ \begin{array}{ccccc} \frac{6}{5} & \frac{6}{5}\\ \frac{6}{5} & \frac{6}{5} \\ \end{array} \right] c=[56565656]
求出c的特征值和单位特征向量,将单位特征向量按列排序(按照特征值大小进行排序),得到的单位特征向量为:
特征向量为 = 1 2 [ 1 − 1 1 − 1 ] 特征向量为=\frac{1}{\sqrt[]{2}}\left [ \begin{array}{ccccc} 1 & -1\\ 1 & -1 \\ \end{array} \right] 特征向量为=21[11−1−1]
取出第一列组成矩阵p,然后
y =pT*x,y即为我们所需要的降维之后的数据
y = 1 2 [ 1 1 ] ∗ [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] = 1 2 [ − 3 − 1 0 3 1 ] y=\frac{1}{\sqrt[]{2}}\left [ \begin{array}{ccccc} 1 & 1\\ \end{array} \right] * \left[ \begin{array}{cccccccccccc} -1 & -1 & 0 & 2 &0\\ -2 & 0 & 0 & 1 &1 \end{array} \right] =\frac{1}{\sqrt[]{2}}\left[ \begin{array}{cccccccccccc} -3 & -1 & 0 & 3 & 1 \end{array} \right] y=21[11]∗[−1−2−10002101]=21[−3−1031]
可以看到 PCA与LDA降维所得到的答案是一样的,证明了我们计算的正确性
码字不易,主要是写latex的语法的矩阵实在是太复杂了,写的十分折磨,点个赞再走把!
相关文章:
)
PCA和LDA数据降维计算(含数学例子推导过程)
PCA算法和LDA算法可以用于对数据进行降维,例如可以把一个2维的数据降低维度到一维,本文通过举例子来对PCA算法和LDA算法的计算过程进行教学展示。 PCA算法计算过程(文字版,想看具体计算下面有例子) 1.将原始数据排列成n行m列的矩阵…...
题目 1053: 二级C语言-平均值计算(python详解)——练气三层初期
✨博主:命运之光 🦄专栏:算法修炼之练气篇(C\C版) 🍓专栏:算法修炼之筑基篇(C\C版) 🍒专栏:算法修炼之练气篇(Python版) ✨…...
Python —— UI自动化之Page Object模式
1、Page Object模式简介 1、二层模型 Page Object Model(页面对象模型), 或者也可称之为POM。在UI自动化测试广泛使用的一种分层设计 模式。核心是通过页面层封装所有的页面元素及操作,测试用例层通过调用页面层操作组装业务逻辑。 1、实战 …...

职能篇—自动驾驶产品经理
自动驾驶产品开发流程 在讲自动驾驶产品经理之前,先简单了解一下自动驾驶的开发体系。如上图所示,从产品需求开始,经由系统需求、系统架构、软件需求、软件架构,最终分解到软件代码实现模块,再经由MIL、SIL、HIL、VIL完…...

ubuntu安装golang
看版本:https://go.dev/dl/ 下载: wget https://go.dev/dl/go1.21.3.linux-amd64.tar.gz卸载已有的go,可以apt remove go,也可以which go之后删除那个go文件,然后: rm -rf /usr/local/go && tar…...

ES 8 新特性
1. async 和 await async 和 await 两种语法结合可以让异步代码像同步代码一样。(即:看起来是同步的,实质上是异步的。) 先从字面意思理解,async 意为异步,可以用于声明一个函数前,该函数是异步的。await 意为等待,即等待一个异步方法完成。 1.1 async async 声明(…...

linux-防火墙
目录 一、防火墙概念 1.软件防火墙 2.iptables默认规则 3.iptables的五链 4.iptables动作 5.四表五链 6.iptables实例 一、防火墙概念 linux下防火墙一般分为软件防火墙、硬件防火墙 硬件防火墙:在硬件的级别实现防火墙过滤功能,性能高…...
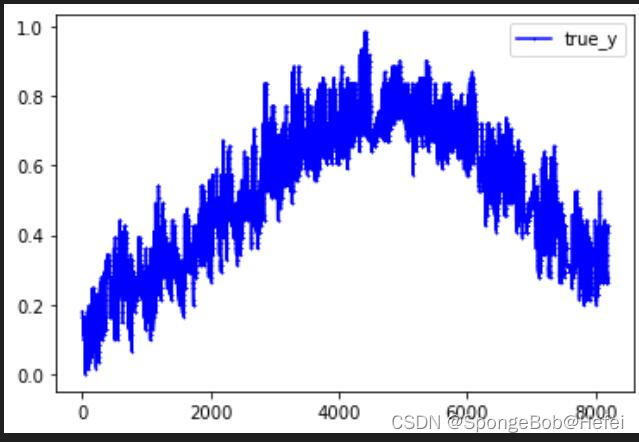
Pytorch--3.使用CNN和LSTM对数据进行预测
这个系列前面的文章我们学会了使用全连接层来做简单的回归任务,但是在现实情况里,我们不仅需要做回归,可能还需要做预测工作。同时,我们的数据可能在时空上有着联系,但是简单的全连接层并不能满足我们的需求࿰…...
)
爬虫进阶-反爬破解9(下游业务如何使用爬取到的数据+数据和文件的存储方式)
一、下游业务如何使用爬取到的数据 (一)常用数据存储方案 1.百万级别数据:单机数据库,搭建和使用方便快捷,成本低 2.千万级别数据:负载均衡的多台数据库,安全和稳定 3.海量数据:…...

Docker常用应用部署
Docker常用应用部署 一、Ubuntu系统Docker快速安装 Docker官网安装文档:https://docs.docker.com/engine/install/ubuntu/ # 文本处理的流编辑器 -i直接修改读取的文件内容,而不是输出到终端 # sed -i s/原字符串/新字符串/ /home/1.txt # 下面这个是修…...
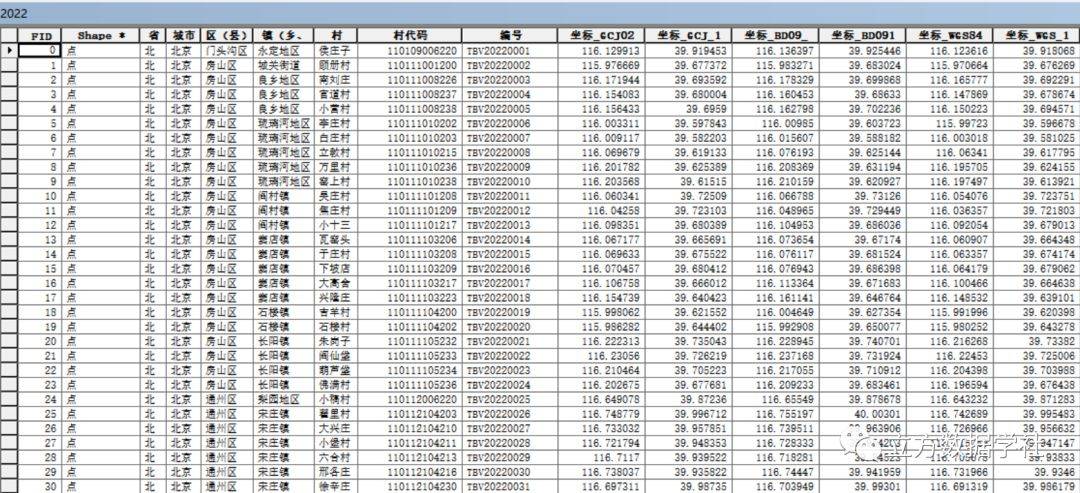
【数据分享】2014-2022年我国淘宝村点位数据(Excel格式/Shp格式)
电子商务是过去一二十年我国发展最快的行业,其中又以淘宝为代表,淘宝的发展壮大带动了一大批服务淘宝电子商务的村庄,这些村庄被称为淘宝村! 截至到目前,阿里研究院梳理并公布了2014-2022年共9个年份的淘宝村名单&…...
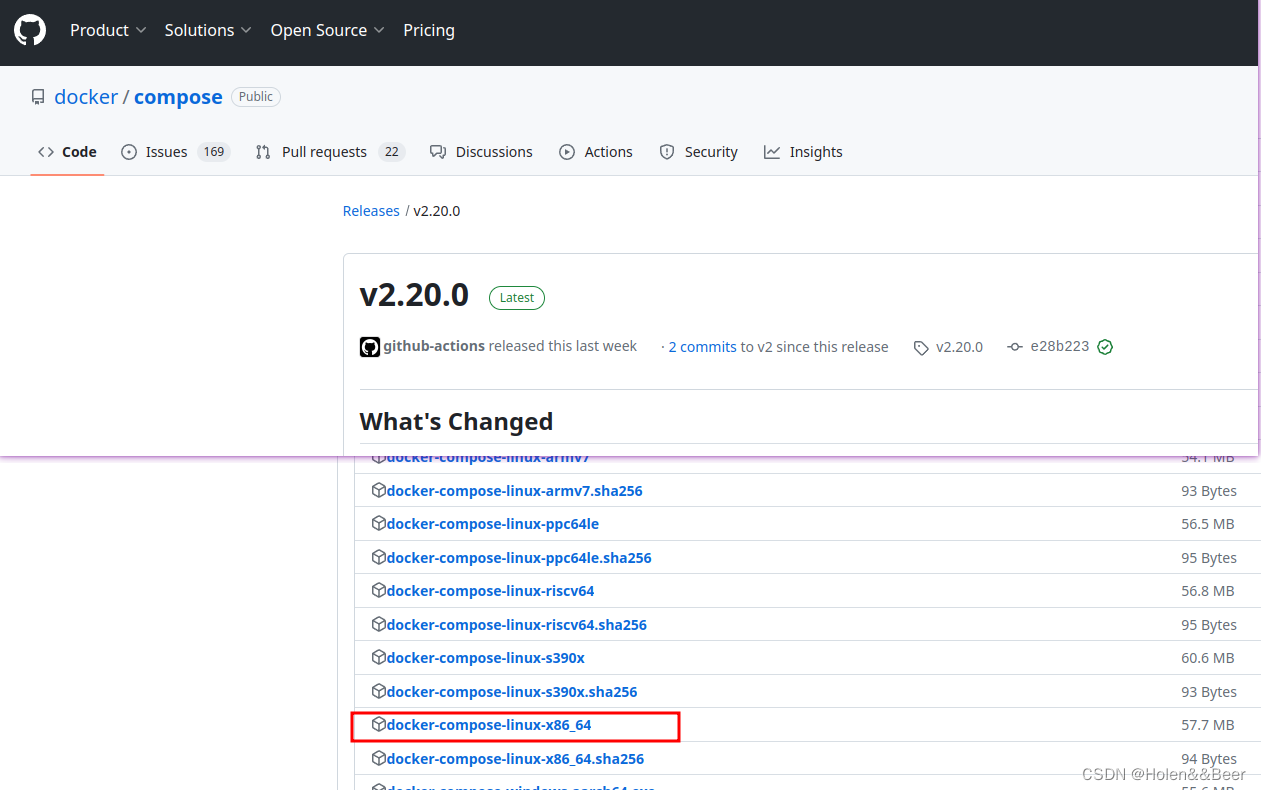
Ubuntu 安装 docker-compose
在Ubuntu上安装Docker Compose,可以按照以下步骤进行操作: 下载 Docker Compose 二进制文件 sudo curl -L "https://github.com/docker/compose/releases/latest/download/docker-compose-$(uname -s)-$(uname -m)" -o /usr/local/bin/docker…...

vue2、vue3中路由守卫变化
什么是路由守卫? 路由守卫就是路由跳转的一些验证,比如登录鉴权(没有登录不能进入个人中心页)等等等 路由守卫分为三大类: 全局守卫:前置守卫:beforeEach 后置钩子:afterEach 单个…...

Leetcode—547.省份数量【中等】
2023每日刷题(八) Leetcode—547.省份数量 实现代码 static int father[210] {0};int Find(int x) {if(x ! father[x]) {father[x] Find(father[x]);}return father[x]; }void Union(int x, int y) {int a Find(x);int b Find(y);if(a ! b) {fathe…...
Nginx 防盗链
nginx防盗链问题 盗链: 就是a网站有一张照片,b网站引用了a网站的照片 。 防盗链: a网站通过设置禁止b网站引用a网站的照片。 nginx防止网站资源被盗用模块 ngx_http_referer_module 如何区分哪些是不正常的用户? HTTP Referer…...
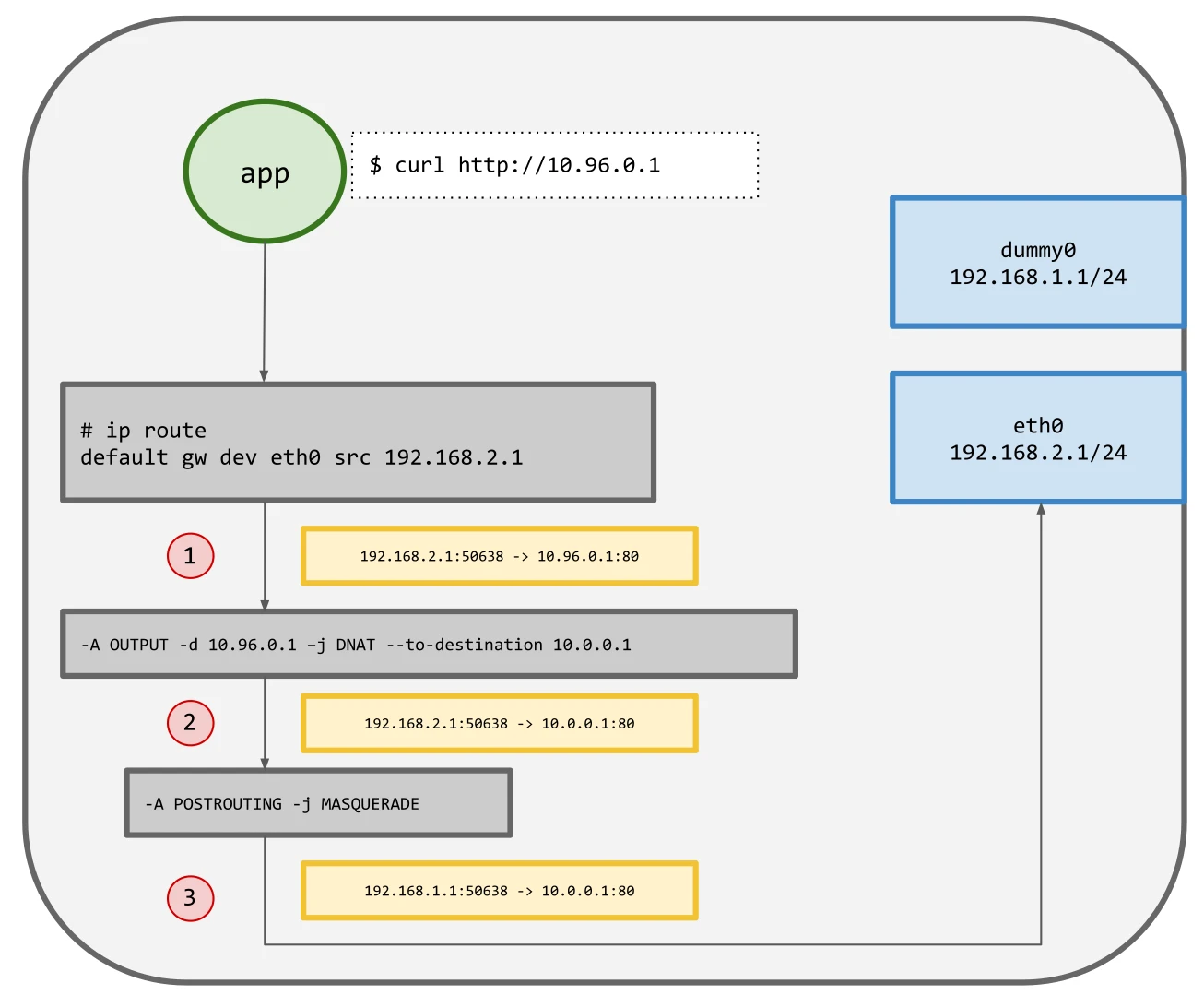
26. 通过 cilium pwru了解网络包的来龙去脉
pwru是一种基于eBPF的工具,可跟踪Linux内核中的网络数据包,并具有先进的过滤功能。它允许对内核状态进行细粒度检查,以便通过调试网络连接问题来解决传统工具(如iptables TRACE或tcpdump)难以解决甚至无法解决的问题。在本文中,我将介绍pwru如何在不必事先了解所有内容的…...

刷题笔记day01-数组
704 题 主要强调,左闭右闭的情况,就是每次查询都会和 [left, right] 进行比较。所以后面的都是mid-1,mid1 的情况。 package mainfunc search(nums []int, target int) int {// 二分查找方法// 每次查找都是左闭右闭的情况left : 0right : …...

C#调用C++ 的DLL传送和接收中文字符串
1 c#向c传送中文字符串 设置:将 字符集 改为 使用多字节字符集 cpp代码: extern "C"_declspec(dllexport) int input_chn_str(char in_str[]) {cout<<in_str<<endl;return 0; }c#代码: [DllImport("Demo.dll…...

【MySQL】数据库常见错误及解决
目录 2003错误:连接错误1251错误:身份验证错误1045错误:拒绝访问错误服务没有报告任何错误net start mysql 发生系统错误 5。 1064错误:语法错误1054错误:列名不存在1442错误:触发器中不能对本表增删改1303…...
spring常见问题汇总
1. 什么是spring? Spring是一个轻量级Java开发框架,最早有Rod Johnson创建,目的是为了解决企业级应用开发的业务 逻辑层和其他各层的耦合问题。它是一个分层的JavaSE/JavaEE full-stack(一站式)轻量级开源框架, 为开…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
