图的应用1.0-----最小生成树问题
目录
前言
生成树
1.基本概念
2.生成树的特点
3.生成树形成过程
最小生成树(Minimum Spanning Tree)
1.基本概念
2.构造方法(MST)
普里姆(Prime)算法
1.算法思想
2.代码实现
克鲁斯卡尔(Kruskal)算法
1.算法思想
2.代码实现
Prime算法与Kruskal算法比较
前言
今天我们学习图的应用,对于最小生成树问题,那什么是最小生成树呢?图又这么去实现一个生成树和最小生成树?下面我们就一起来看看。
生成树
1.基本概念
生成树:所有顶点均由边连接在一起,但不存在回路的图。
 如上图所示,除了第一个不是生成树(因为存在环),其他都是生成树。
如上图所示,除了第一个不是生成树(因为存在环),其他都是生成树。
2.生成树的特点
图的生成树有以下特点:
- 一个图可以有许多棵不同的生成树
- 生成树的顶点个数与图的顶点个数相同
- 生成树是图的极小连通子图,去掉一条边则非连通
- 一个有n个顶点的连通图的生成树有n-1条边
- 在生成树中再加一条边必然形成回路。
- 生成树中任意两个顶点间的路径是唯一的
3.生成树形成过程
形成过程:
设图G=(V,E)是个连通图,当从图任一顶点出发遍历图G时,将边集E(G)分成两个集合T(G)和B(G)。其中T(G)是遍历图时所经过的边的集合,B(G)是遍历图时未经过的边的集合。显然,G1(V,T)是图G的极小连通子图。即子图G1是连通图G的生成树。

最小生成树(Minimum Spanning Tree)
1.基本概念
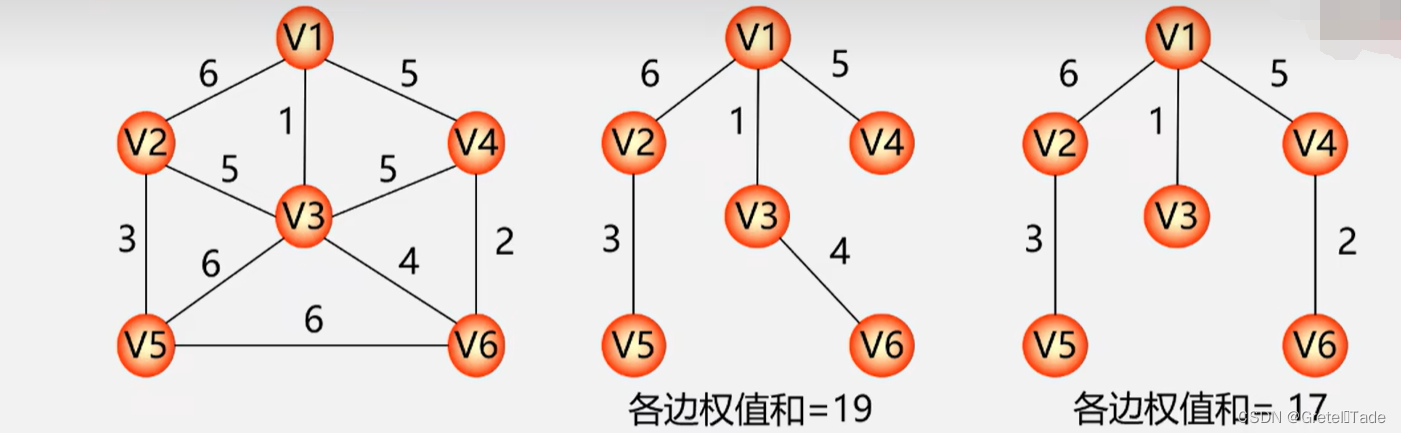
最小生成树:给定一个无向网络,在该网的所有生成树中,使得各边权值之和最小的那棵生成树称为该网的最小生成树,也叫最小代价生成树。
如图所示,连通图的最小生成树权值之和为17才是最小生成树
2.构造方法(MST)
最小生成树(Minimum Spanning Tree),根据其英文名字有一个叫MST算法用于去构造最小生成树,MST算法本质是一种贪心算法,根据贪心算法的方式去获取到最优解。
MST 性质:设N= (V,E)是一个连通网,U是顶点集V的一个非空子集。若边(u, v)是一条具有最小权值的边,其中uEu,vEV-U,则必存在一棵包含边(u, v)的最小生成树。

MST解释说明:
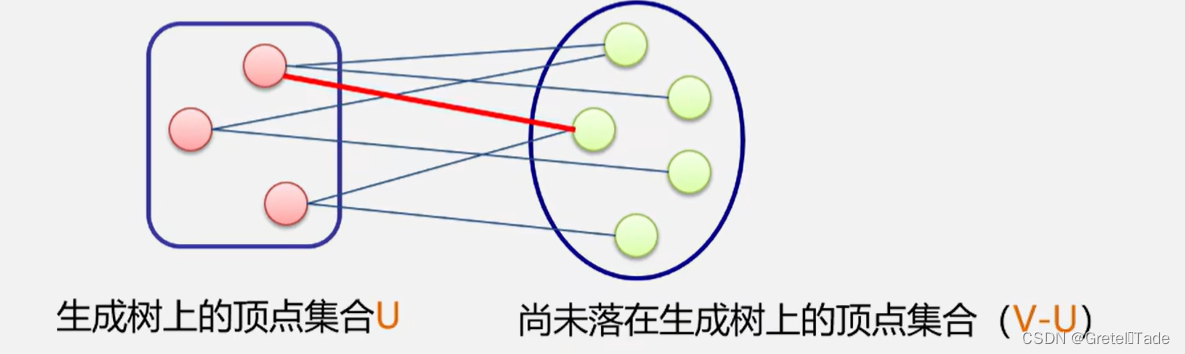
在生成树的构造过程中,图中n个顶点分属两个集合:
- 已落在生成树上的顶点集:u ·已落在生成树上的顶点集:U
- 尚未落在生成树上的顶点集:V-U ·尚未落在生成树上的顶点集:V-U
接下来则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边 接下来则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边
下面我就介绍两种MST算法,分别是Prim算法和Kruskal算法。
以下代码是一个图的邻接矩阵创建代码:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define Maxint 32767
#define Maxnum 100//最大顶点数//数据类型
typedef struct d {char id[10];//……
}
ElemType;
//图的邻接数组
typedef struct graph {ElemType vexs[Maxnum];//图数据int matrix[Maxnum][Maxnum];//二维数组int vexnum;//点数int arcnum;//边数
}Graph;//节点id查找下标
int Locate_vex(Graph G, char* id) {for (int i = 0; i < G.vexnum; i++)if (strcmp(G.vexs[i].id, id) == 0)return i;return -1;
}//构造邻接矩阵(无向图,对称矩阵)(有向图)赋权图
void Create_graph(Graph* G) {printf("请输入顶点个数和边的个数:\n");scanf("%d %d", &G->vexnum, &G->arcnum);//输入点数边数printf("请输入顶点数据:\n");for (int i = 0; i < G->vexnum; i++) {scanf("%s", G->vexs[i].id);}for (int x = 0; x < G->vexnum; x++) {for (int y = 0; y < G->vexnum; y++) {if (x == y)G->matrix[x][y] = 0;//对角线初始化为0elseG->matrix[x][y] = Maxint;//其他初始化为Maxint}}printf("请输入边相关数据:\n");for (int k = 0; k < G->arcnum; k++) {char a[10], b[10];int w;scanf("%s %s %d", a, b, &w);//a->bint i = Locate_vex(*G, a);int j = Locate_vex(*G, b);//矩阵赋值G->matrix[i][j] = w;G->matrix[j][i] = w;//删掉这个,表示有向图}
}//输出矩阵
void print_matrix(Graph G) {printf("矩阵为:\n");for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {if(G.matrix[i][j]==Maxint)printf("∞\t");elseprintf("%d\t", G.matrix[i][j]);}printf("\n");}printf("图的顶点个数和边数:%d,%d\n", G.vexnum, G.arcnum);
}//遍历
void visit(Graph G, int loca) {printf("%s ", G.vexs[loca].id);
}普里姆(Prime)算法
1.算法思想
Prime算法的核心步骤是:在带权连通图中V是包含所有顶点的集合, U已经在最小生成树中的节点,从图中任意某一顶点v开始,此时集合U={v},重复执行下述操作:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边,将(u,w)这条边加入到已找到边的集合,并且将点w加入到集合U中,当U=V时,就找到了这颗最小生成树
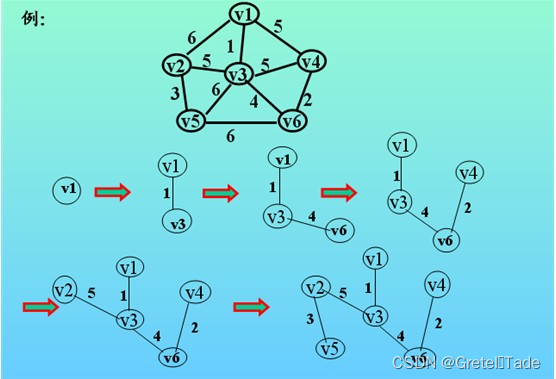
其实,算法的核心步骤就是:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边。
过程如下图所示:
2.代码实现
//最小生成树
//生成树
typedef struct shortedge {char adjvex_id[10];//储存到的数据idint lowcost;//到其他顶点最短路径距离
}ShortEdge;
//01---Prim算法
//在U集合中找到距离其他顶点最近的下一个顶点位置
int min_path(Graph G, ShortEdge* shortedge) {int location;int min = Maxint;for (int i = 1; i < G.vexnum; i++) {if (min > shortedge[i].lowcost && shortedge[i].lowcost != 0) {min = shortedge[i].lowcost;location = i;}}return location;
}
//Prim接口
void MST_Prim(Graph G, char* start) {printf("(Prim)最小生成树如下:\n");ShortEdge shortdege[Maxnum];//集合Uint sum = 0;//统计最短路径权之和//对第一个起始数据start初始化处理,把第一个顶点放入到集合U当中int k = Locate_vex(G, start);//当前集合U只有顶点start,那么里面的数据就储存start的数据for (int i = 0; i < G.vexnum; i++) {strcpy(shortdege[i].adjvex_id, start);shortdege[i].lowcost = G.matrix[k][i];}shortdege[k].lowcost = 0;//此顶点对应的下标标记为0,表示已经加入集合U当中//后继处理for (int i = 0; i < G.vexnum-1; i++) {//找到下一个离集合U最近的顶点,下标为kk = min_path(G, shortdege);sum += shortdege[k].lowcost;printf("%s->%s %d\n", shortdege[k].adjvex_id, G.vexs[k].id, shortdege[k].lowcost);shortdege[k].lowcost = 0;//此顶点对应的下标标记为0,表示已经加入集合U当中//加入了新的顶点后,对集合U到其他顶点最近距离的值进行更新for (int j = 0; j < G.vexnum; j++) {if (G.matrix[k][j] < shortdege[j].lowcost && shortdege[j].lowcost!=0) {shortdege[j].lowcost = G.matrix[k][j];strcpy(shortdege[j].adjvex_id, G.vexs[k].id);}}}printf("最小生成树权之和为:%d\n", sum);
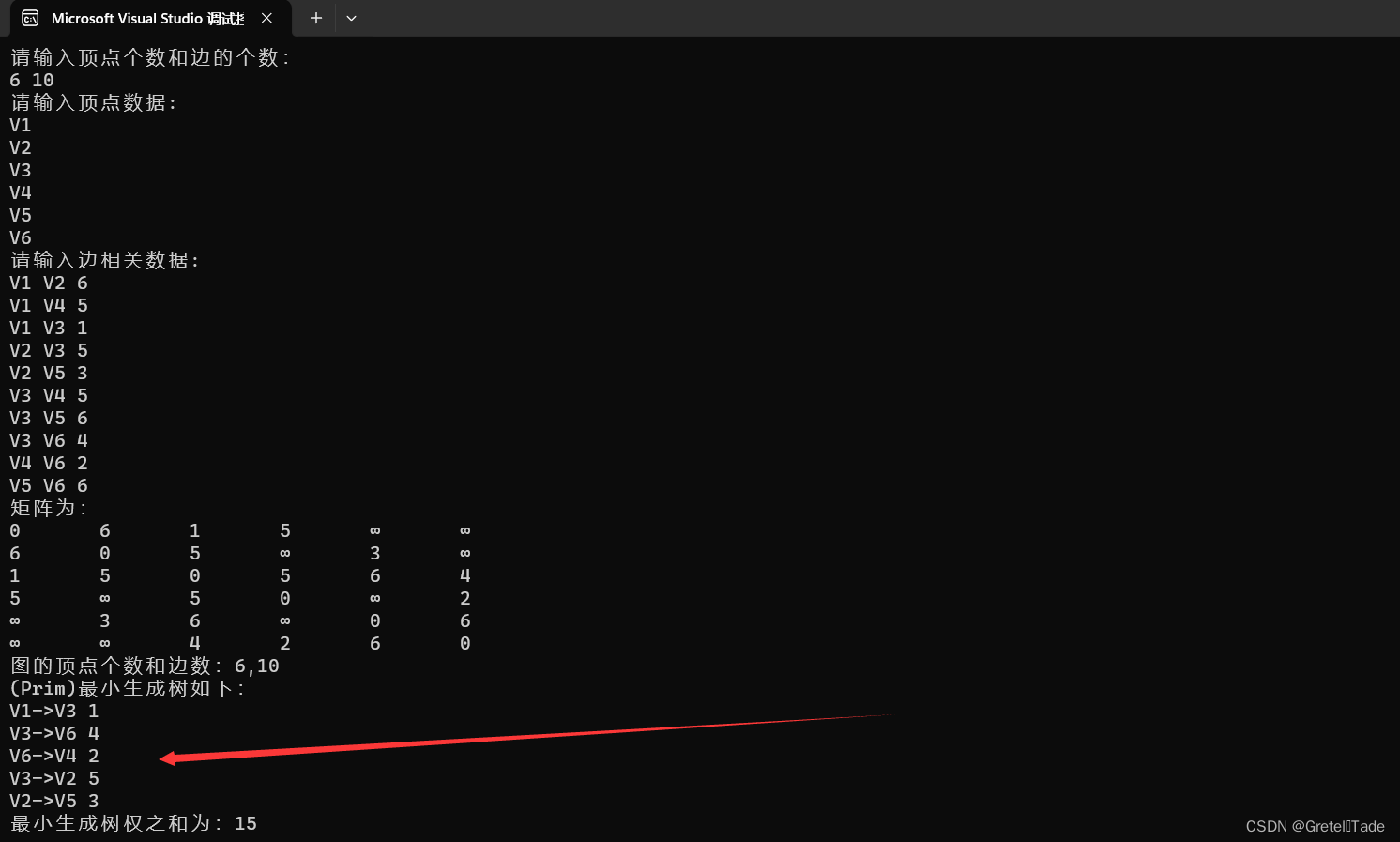
}测试结果:
int main() {Graph G;Create_graph(&G);print_matrix(G);MST_Prim(G, "V1");
}
克鲁斯卡尔(Kruskal)算法
1.算法思想
克鲁斯卡尔算法是一种用于求解最小生成树问题的贪心算法。 最小生成树是一个连通图的生成树,其边的权重之和最小。 一、原理 克鲁斯卡尔算法的核心思想是按照边的权重从小到大逐渐选择连通图的边,直到所有顶点都被连接为止。 在每一步中,选择当前权重最小的边,若该边的两个顶点尚未连接,则将其添加到最小生成树的边集合中,并将这两个顶点归为同一个连通分量。克鲁斯卡尔(Kruskal)算法又称作为避圈法。
过程如下: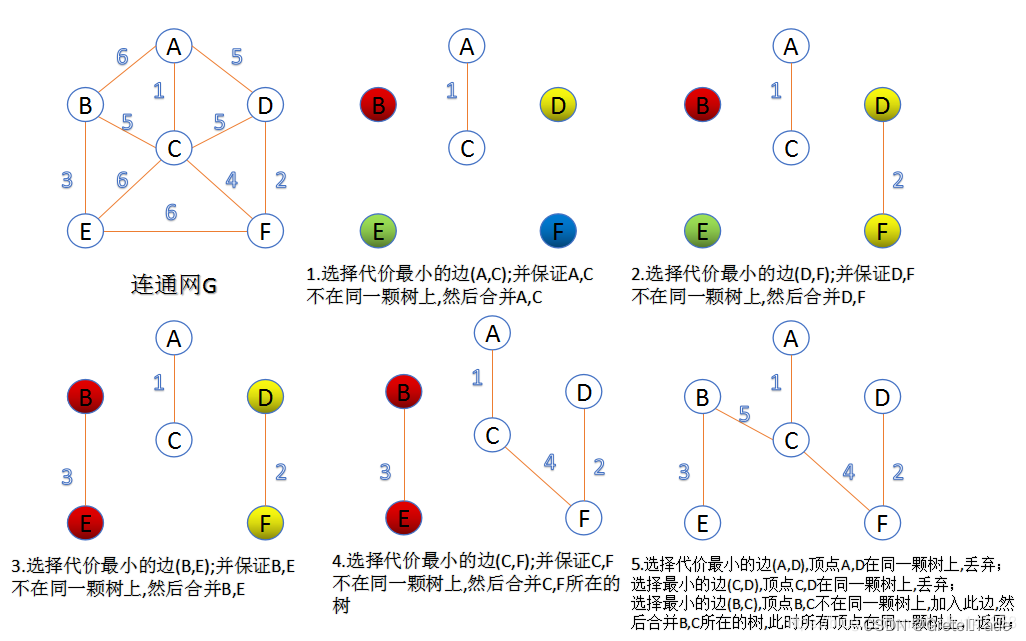
2.代码实现
这里就需要对边进行权值的大小排序,直接就用快速排序去进行排序,(头文件.h)如下:
#pragma once
//边的结构体数据
typedef struct edge {char begin_id[10];//边起点的idchar end_id[10];//边终点的idint weight;//权值
}Edge;
void quick_sort(Edge* n, int left, int right);
快速排序源文件.c代码如下:
#include"sort.h"
//快速排序---递归实现
void quick_sort(Edge* n, int left, int right) {int i, j, temp;i = left;j = right;if (i > j) {return;}else {temp = n[left].weight;while (i != j) {while (n[j].weight >= temp && i < j)//先向左移动jj--;while (n[i].weight <= temp && i < j) //再向右移动ii++;if (i < j) {//此时对i和j指向的数字进行数字交换Edge num = n[i];n[i] = n[j];n[j] = num;}}//当i和j相遇的时候就结束循环//此时i与j相遇,就与temp交换Edge new_temp = n[i];n[i] = n[left];n[left] = new_temp;}//最后左右边依次进入到递归quick_sort(n, left, i - 1); //左边的数字都比temp要小quick_sort(n, i + 1, right); //右边的数字都比temp要大
}克鲁斯卡尔(Kruskal)算法代码如下:
//最小生成树//02--Kruskal算法
//对边排序
Edge* arc_sort(Graph G) {//创建边数据Edge* edge = (int*)malloc(sizeof(Edge) * G.arcnum);int count = 0;//把边的数据储存到edge里面(无向图)for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j <= i; j++) {if (G.matrix[i][j] != Maxint && G.matrix[i][j] != 0) {strcpy(edge[count].begin_id, G.vexs[i].id);strcpy(edge[count].end_id, G.vexs[j].id);edge[count].weight = G.matrix[i][j];count++;}}}//对边的权值进行排序quick_sort(edge, 0, count - 1);return edge;
}//接口
void MST_Kruskal(Graph G) {Edge* edge = arc_sort(G);int sum = 0;int vset[Maxnum];//辅助数组判断连通性//初始化为01234……表示开始的时候都不连通for (int i = 0; i < G.vexnum; i++)vset[i] = i;for (int i = 0; i < G.arcnum; i++) {int a = Locate_vex(G, edge[i].begin_id);//a为起点顶点的位置下标int b = Locate_vex(G, edge[i].end_id);//b为这个边终点的位置下标int v1 = vset[a];//辅助数组中找到起点的连通标准int v2 = vset[b];//辅助数组中找到终点的连通标准//判断v1与v2是否相等,判定是否成环if (v1!=v2) {printf("%s——%s %d\n", edge[i].begin_id, edge[i].end_id, edge[i].weight);sum += edge[i].weight;for (int j = 0; j < G.vexnum; j++) {//与v1连通的数据全部改成v2,表示整体连通if (vset[j] == v1)vset[j] = v2;}}}printf("最小生成树的权值之和:%d\n", sum);//释放空间free(edge);edge = NULL;
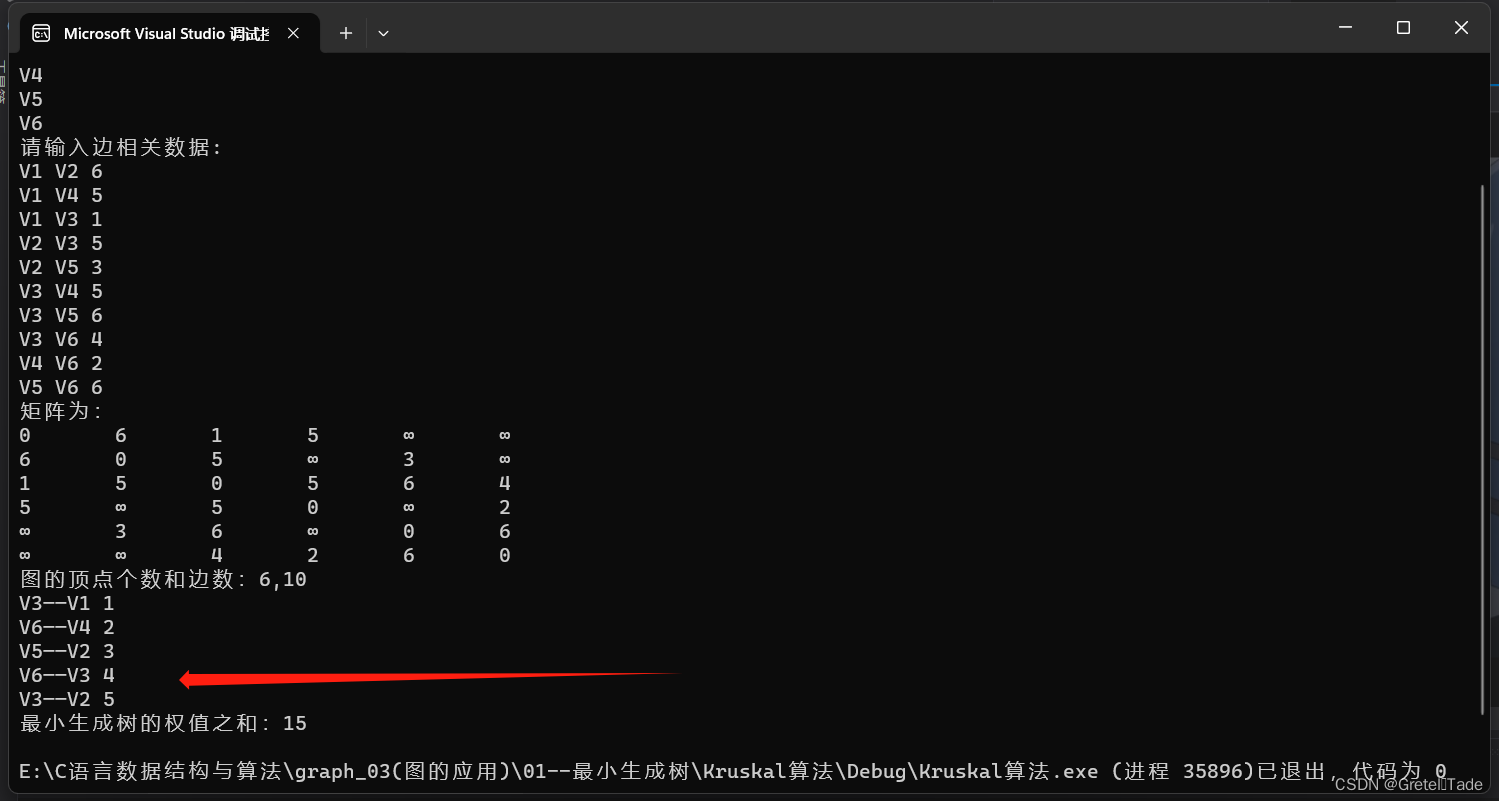
}测试结果:
int main() {Graph G;Create_graph(&G);print_matrix(G);MST_Kruskal(G);
}
Prime算法与Kruskal算法比较

以上就是本期的全部内容了,我们下一次见!
分享一张壁纸:

相关文章:

图的应用1.0-----最小生成树问题
目录 前言 生成树 1.基本概念 2.生成树的特点 3.生成树形成过程 最小生成树(Minimum Spanning Tree) 1.基本概念 2.构造方法(MST) 普里姆(Prime)算法 1.算法思想 2.代码实现 克鲁斯卡尔(Kruskal)算法 1.算法思想 2.代码…...
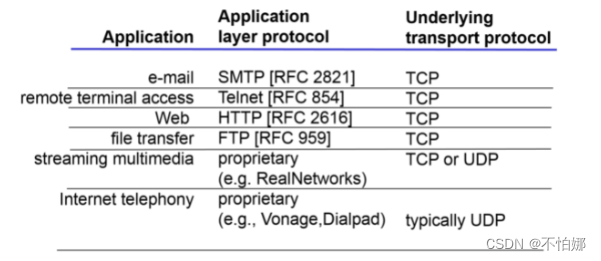
【计算机网络笔记】网络应用对传输服务的需求
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...

IDEA启动报错:Command line is too long的解决办法
文章目录 1.报错现象2.解决办法验证3.最佳实践4.问题原因5.参考文献1.报错现象 在idea中启动一个spring cloud项目时,编译完成后直接报错,报错内容如下: Error running XXXApplication:Command line is too long. Shorten command line for XXXApplication or also for Sp…...

Android 中的 本地广播LocalBroadcastManager
Android 中的 本地广播LocalBroadcastManager 文章目录 Android 中的 本地广播LocalBroadcastManager一、LocalBroadcastManager 的基本作用二 、LocalBroadcastManager 的基本使用1、包的导入(1)Android 源码中bp文件的导入:(2&a…...
题目 1120: C语言训练-“水仙花数“问题2python详解)——练气三层后期
✨博主:命运之光 🦄专栏:算法修炼之练气篇(C\C版) 🍓专栏:算法修炼之筑基篇(C\C版) 🍒专栏:算法修炼之练气篇(Python版) ✨…...

sheng的学习笔记-【中】【吴恩达课后测验】Course 3 - 结构化机器学习项目 - 第二周测验
课程3_第2周_测验题 目录:目录 要解决的问题 ① 为了帮助你练习机器学习的策略,本周我们将介绍另一个场景,并询问你将如何行动。 ② 我们认为这个在机器学习项目中工作的“模拟器”将给出一个任务,即领导一个机器学习项目可能…...

基于Pytorch的驾驶员分心行为实时检测
本文使用深度学习和Pytorch(PyTorch 2.0.1\Torchvision 0.15.2)实时检测驾驶员的分心行为,并附录完整代码。 检测分心驾驶是现代汽车中最重要的功能之一。无论是自动驾驶汽车还是其它高端汽车,都配备了驾驶员监控系统,以持续跟踪驾驶员的行为。这对确保驾驶员保持目光在道路…...
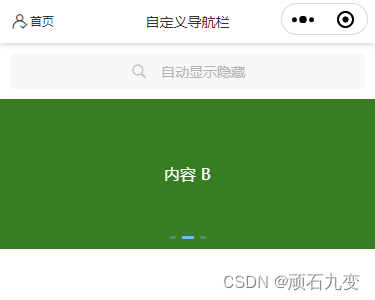
【uniapp】小程序开发7:自定义组件、自动注册组件
一、自定义轮播图组件、自动注册 以首页轮播图组件为例。 1、创建组件文件src/components/my-swipper.vue 代码如下: <template><view><view class"uni-margin-wrap"><swiper class"swiper" circular :indicator-dots…...
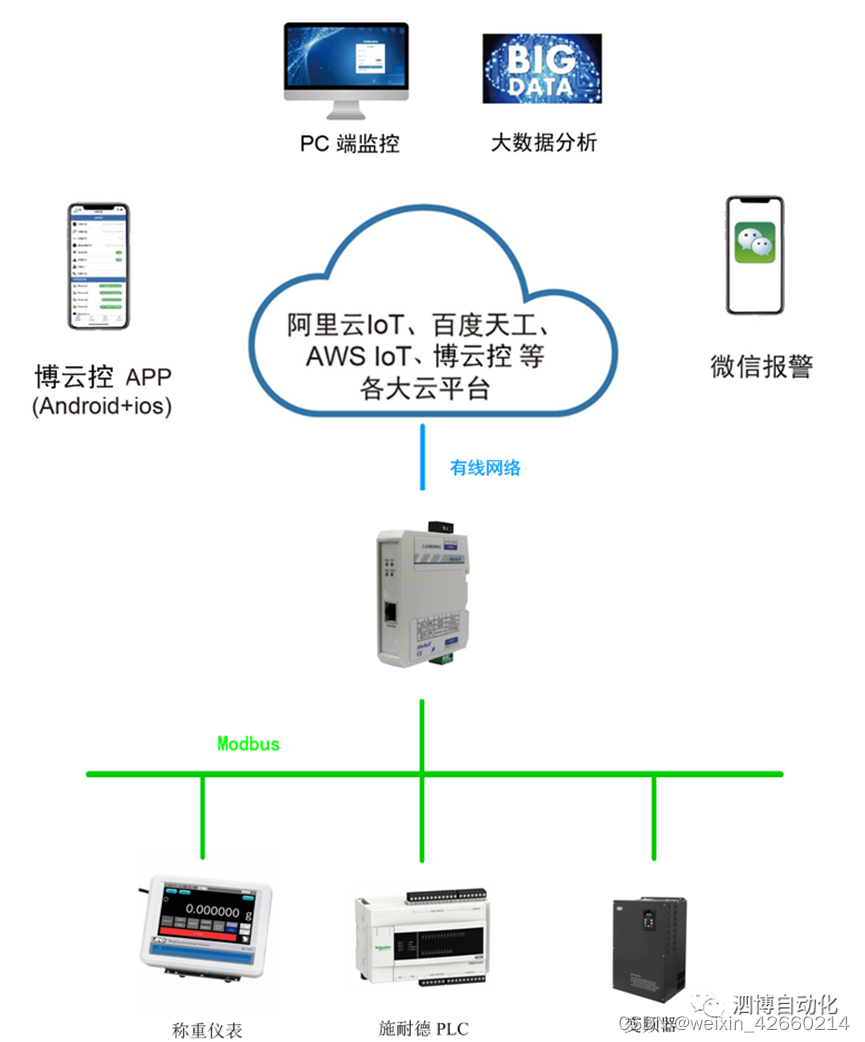
Modbus转MQTT以太网网关MQT-802主要特点和典型应用
随着社会的快速发展,物联网已经潜移默化地深入工控行业的各个领域,其高效的资源整合和强大的数据采集能力,深受客户的喜爱。上海泗博为实现客户在云端平台接收处理世界万物的信息以及实现远程控制,精心打造一款全新物联网产品&…...

Go学习第五章——函数与包
Go学习第五章——函数与包 1 函数1.1 基本语法1.2 函数多返回值1.3 函数的可见性和包级函数1.4 函数调用机制底层原理1.5 值类型和引用类型1.6 注意事项和细节1.7 逃逸机制(补,可不看) 2 包2.1 快速入门2.2 包的使用细节 3 函数详细讲解3.1 递…...

【Python 常用脚本及命令系列 5 -- 如何使用 BeautifulSoup 解析CSDN网页表格中的数据】
文章目录 Python BeautifulSoup 介绍CSDN 网页表格解析开发问题总结 Python BeautifulSoup 介绍 BeautifulSoup是一个Python库,用于解析HTML和XML文档。它常常用于网络爬虫来提取网页中的信息。 以下是BeautifulSoup的一些主要特性: 解析HTMLÿ…...

OpenFeign实现分析、源码解析
什么是openfeign? 是springcloud全家桶的组件之一,其核心作用是为Rest API提供高效简洁的rpc调用方式。 为什么只定义接口而没有实现类? 源码解读(省略) 总结: 源码分析:如何发送http请求? …...

2023 10月最新Vmd 下载安装教程,WindowsLinux
文章目录 下载Vmdwindows版本安装LINUX版本安装 下载Vmd 谷歌搜索VMD 点击左下角download VMD 可选择对应版本 注:点击后会出现输入用户名和密码,由于我已注册,界面不见了,所以直接描述一下。 输入用户名和密码然后会出现让登记…...
Photoshop(PS)安装教程(图文教程超详细)
目录 一.简介 二.安装步骤 软件:PS版本:2023语言:简体中文大小:3.20G系统要求:Win10(1903)及以上版本,64位操作系统硬件要求:CPU2.0GHz 内存8G(或更高,不支…...

C++模版进阶
一、非类型模版参数 之前学习的模版,参数一般是某种类型,但其实非类型的参数也可以定义在模版里面,但也有一定的限制,只可以定义整形家族的参数,而且具有常量性 注意: 1. 浮点数、类对象以及字符串是不允…...
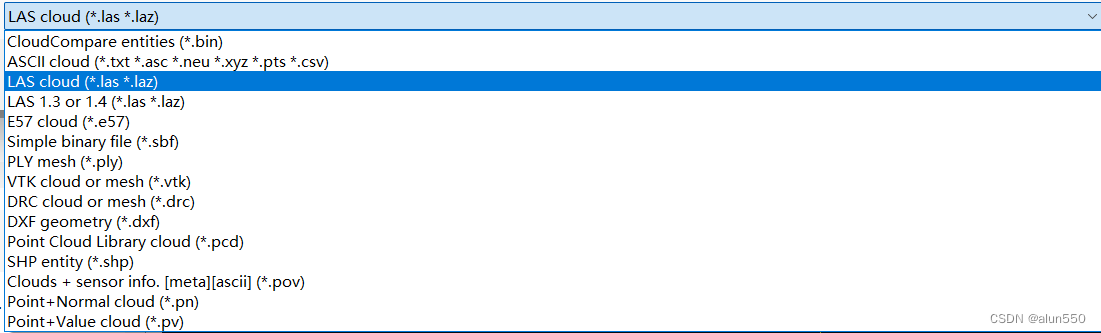
CloudCompare
CloudCompare 源码编译Windows 功能格式转换 源码编译 Windows 源码编译出来的默认基本不带几个插件,包括保存为 .las 的功能 可以直接从 https://www.danielgm.net/cc/ 下载编译好的版本,插件比较多。也有免安装版本 cmake -B build -S . -G "Vi…...
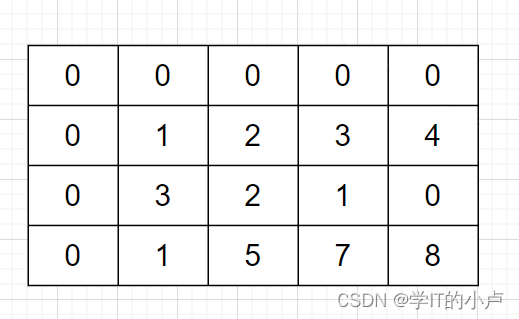
【算法小课堂】深入理解前缀和算法
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。 我们通过一个例子来理解前缀和算法的优势: 一维前缀和: ww…...
元对象系统功能
元对象系统功能 建立工程 布局页面 布局页面 修改原件名称 建立元对象 函数作为接口 增加一些固定的属性 #------------------------------------------------- # # Project created by QtCreator 2023-10-24T21:54:44 # #----------------------------…...

【2024秋招】小米中间件后端开发一面2023-9-13-base武汉
1 自我介绍 2 快手实习 2.1 讲讲你写的curd启动器,做了哪些工作呢 答: 2.2 网上也有一些开源的curd代码生成器,你为什么需要自研呢(重要) 答: (1)这个必须得自研,因…...
SpringMVC Day 01:入门案例
前言 在我们的日常工作和学习中,Web 开发是一个无法回避的重要环节。而在 Java Web 开发领域,SpringMVC 无疑是一个重量级选手。它以其灵活性、强大功能和清晰的 MVC 结构,赢得了大量开发者的青睐。但是,对于初学者来说ÿ…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
