2023 10月最新Vmd 下载安装教程,WindowsLinux
文章目录
- 下载Vmd
- windows版本安装
- LINUX版本安装
下载Vmd
谷歌搜索VMD

点击左下角download VMD
可选择对应版本
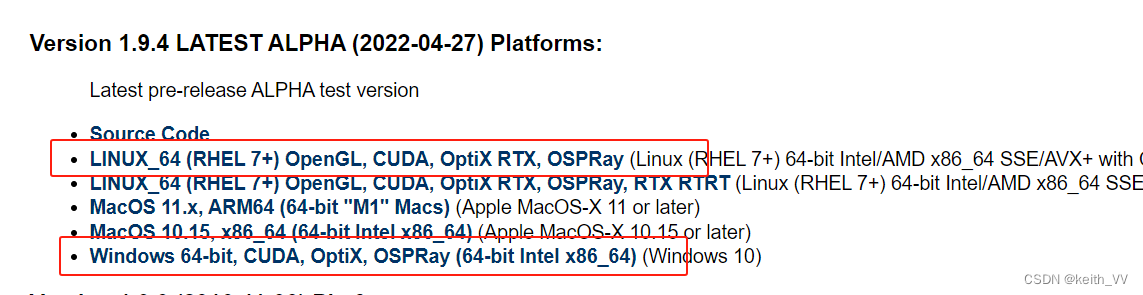
注:点击后会出现输入用户名和密码,由于我已注册,界面不见了,所以直接描述一下。
- 输入用户名和密码
- 然后会出现让登记更详细的信息
- 然后可以选择保存Cookie
- 然后就会出现以下界面
继续点击
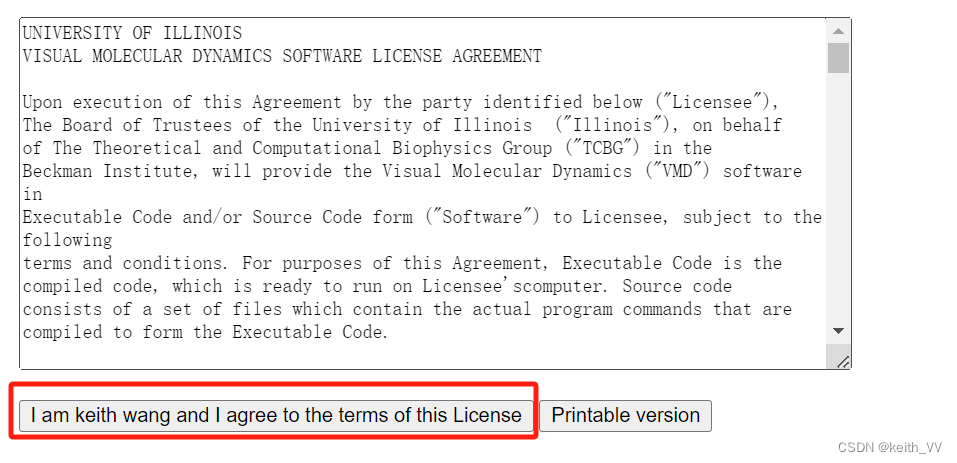
下载

如果前面点击的是LINUX版本,则没有最后一步。
windows版本安装

直接双击安装,连点两次直接装在了C盘(此处我没看到更改路径的步骤,所以我选择在LINUX中重新安装)
LINUX版本安装
1.直接下载好安装包(与windows版本不同,此处是压缩包),然后复制到LINUX中。
2.在压缩包目录下,右键打开终端,输入
tar zxvf vmd-1.9.4a57.bin.LINUXAMD64-CUDA10-OptiX600-RTX2060-2080Ti.tar.gz# 解压压缩包
tar zxvf [fileame]z:表示使用gzip压缩算法解压缩文件。
x:表示解压缩文件。
v:表示在解压缩过程中显示详细信息。
f:表示指定要解压缩的文件以下命令分开输入敲回车
3.输入
cd vmd-1.9.4a57 # 进入解压后的目录
./configure LINUXAMD64
又可能make时显示没有make包,按照命令安装即可
cd src # 进入src文件夹
sudo make install # 若显示权限不足,可在前面加上sudo
# 然后会提示输入密码,注意密码看不见,输完直接回车
5.添加环境变量
echo &PATH # 可查看环境变量
PATH=$PATH:/usr/local/bin/vmd # 添加环境变量/usr/local/bin/vmd
6.查看是否安装成功|运行
vmd
相关文章:

2023 10月最新Vmd 下载安装教程,WindowsLinux
文章目录 下载Vmdwindows版本安装LINUX版本安装 下载Vmd 谷歌搜索VMD 点击左下角download VMD 可选择对应版本 注:点击后会出现输入用户名和密码,由于我已注册,界面不见了,所以直接描述一下。 输入用户名和密码然后会出现让登记…...
Photoshop(PS)安装教程(图文教程超详细)
目录 一.简介 二.安装步骤 软件:PS版本:2023语言:简体中文大小:3.20G系统要求:Win10(1903)及以上版本,64位操作系统硬件要求:CPU2.0GHz 内存8G(或更高,不支…...

C++模版进阶
一、非类型模版参数 之前学习的模版,参数一般是某种类型,但其实非类型的参数也可以定义在模版里面,但也有一定的限制,只可以定义整形家族的参数,而且具有常量性 注意: 1. 浮点数、类对象以及字符串是不允…...
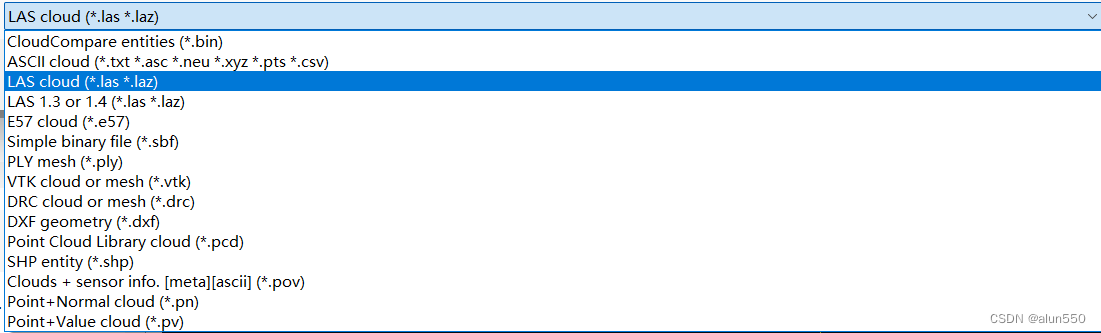
CloudCompare
CloudCompare 源码编译Windows 功能格式转换 源码编译 Windows 源码编译出来的默认基本不带几个插件,包括保存为 .las 的功能 可以直接从 https://www.danielgm.net/cc/ 下载编译好的版本,插件比较多。也有免安装版本 cmake -B build -S . -G "Vi…...
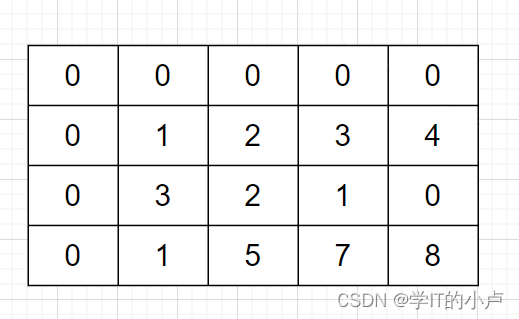
【算法小课堂】深入理解前缀和算法
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。 我们通过一个例子来理解前缀和算法的优势: 一维前缀和: ww…...
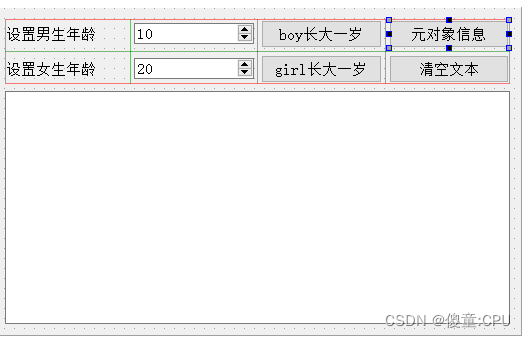
元对象系统功能
元对象系统功能 建立工程 布局页面 布局页面 修改原件名称 建立元对象 函数作为接口 增加一些固定的属性 #------------------------------------------------- # # Project created by QtCreator 2023-10-24T21:54:44 # #----------------------------…...

【2024秋招】小米中间件后端开发一面2023-9-13-base武汉
1 自我介绍 2 快手实习 2.1 讲讲你写的curd启动器,做了哪些工作呢 答: 2.2 网上也有一些开源的curd代码生成器,你为什么需要自研呢(重要) 答: (1)这个必须得自研,因…...
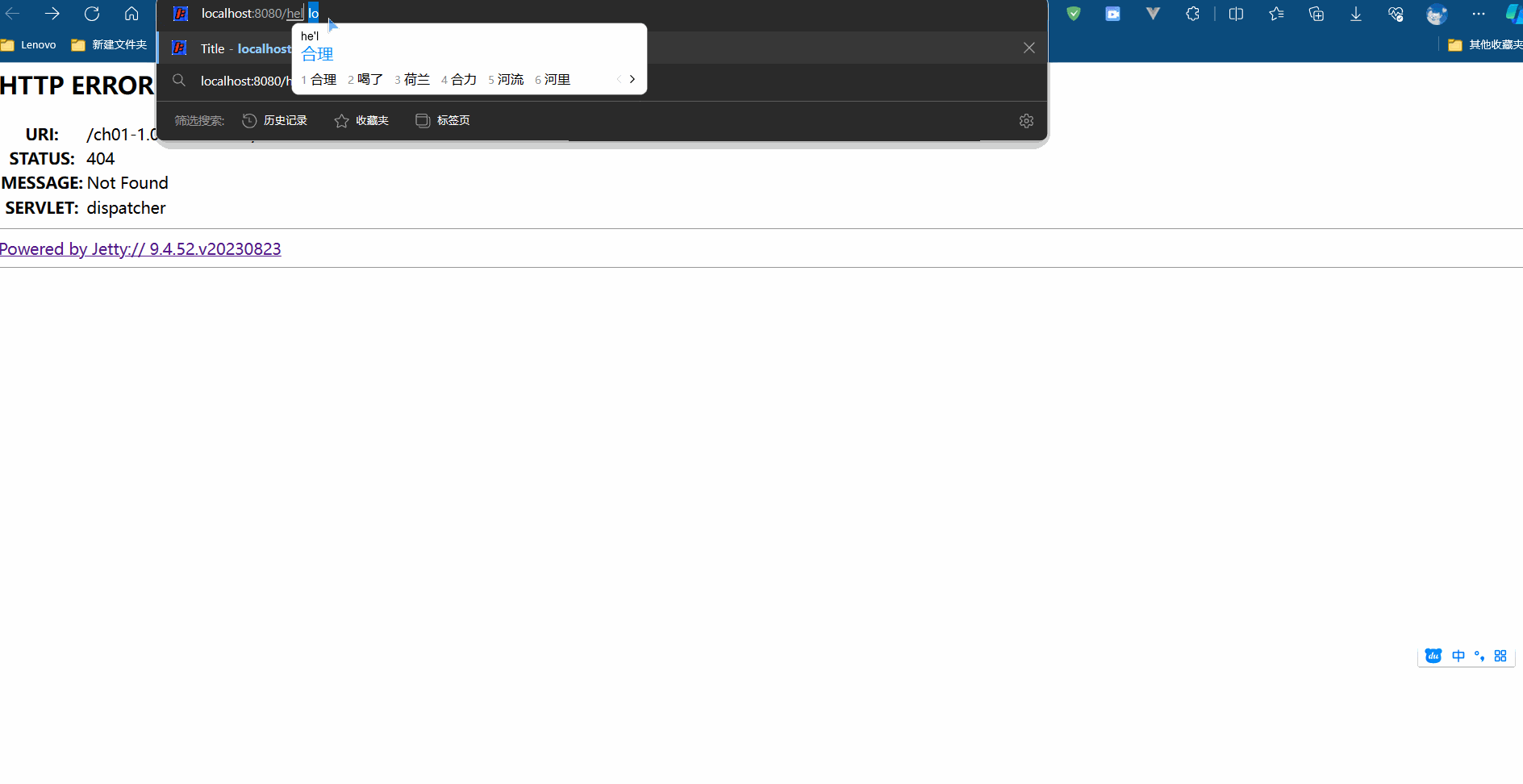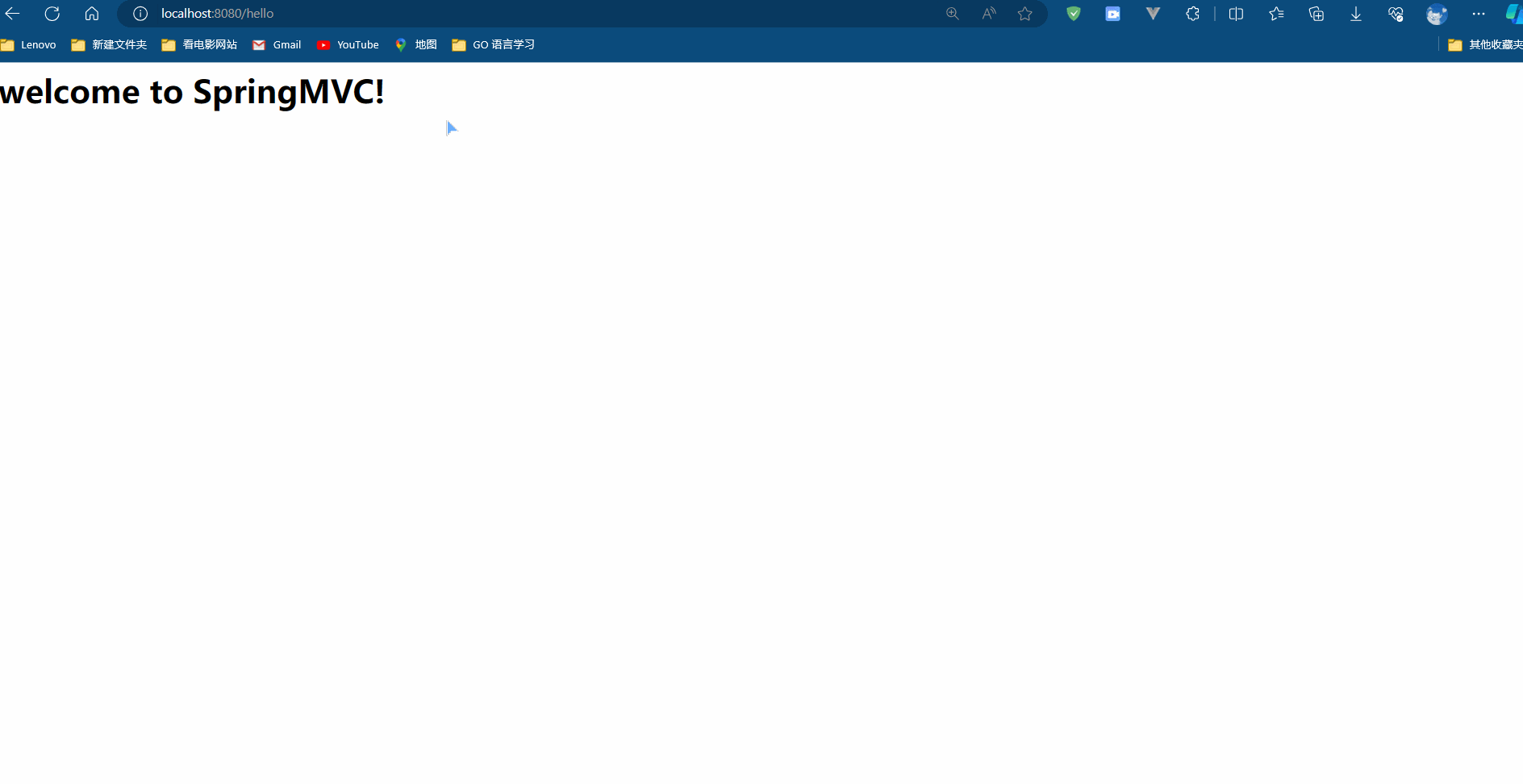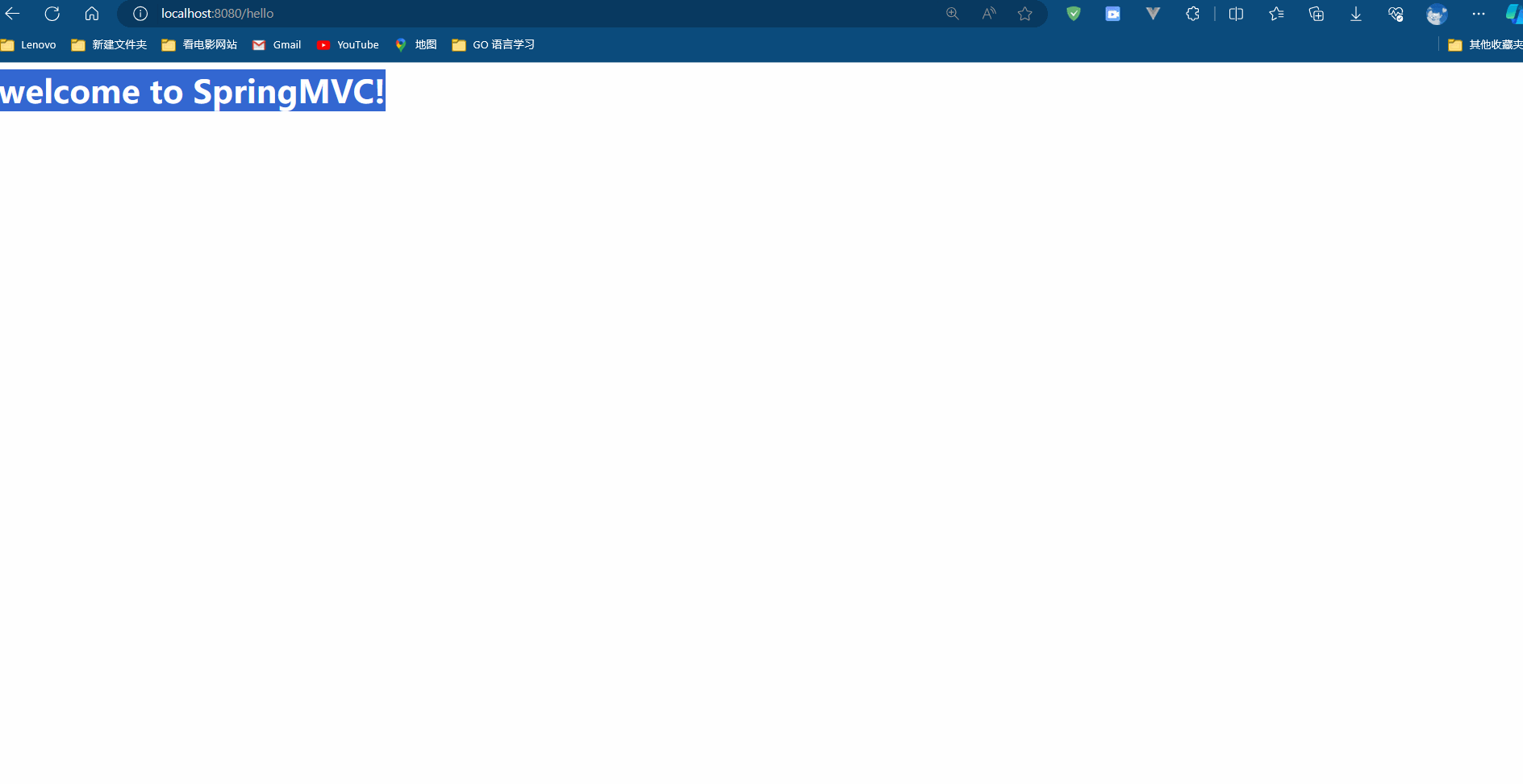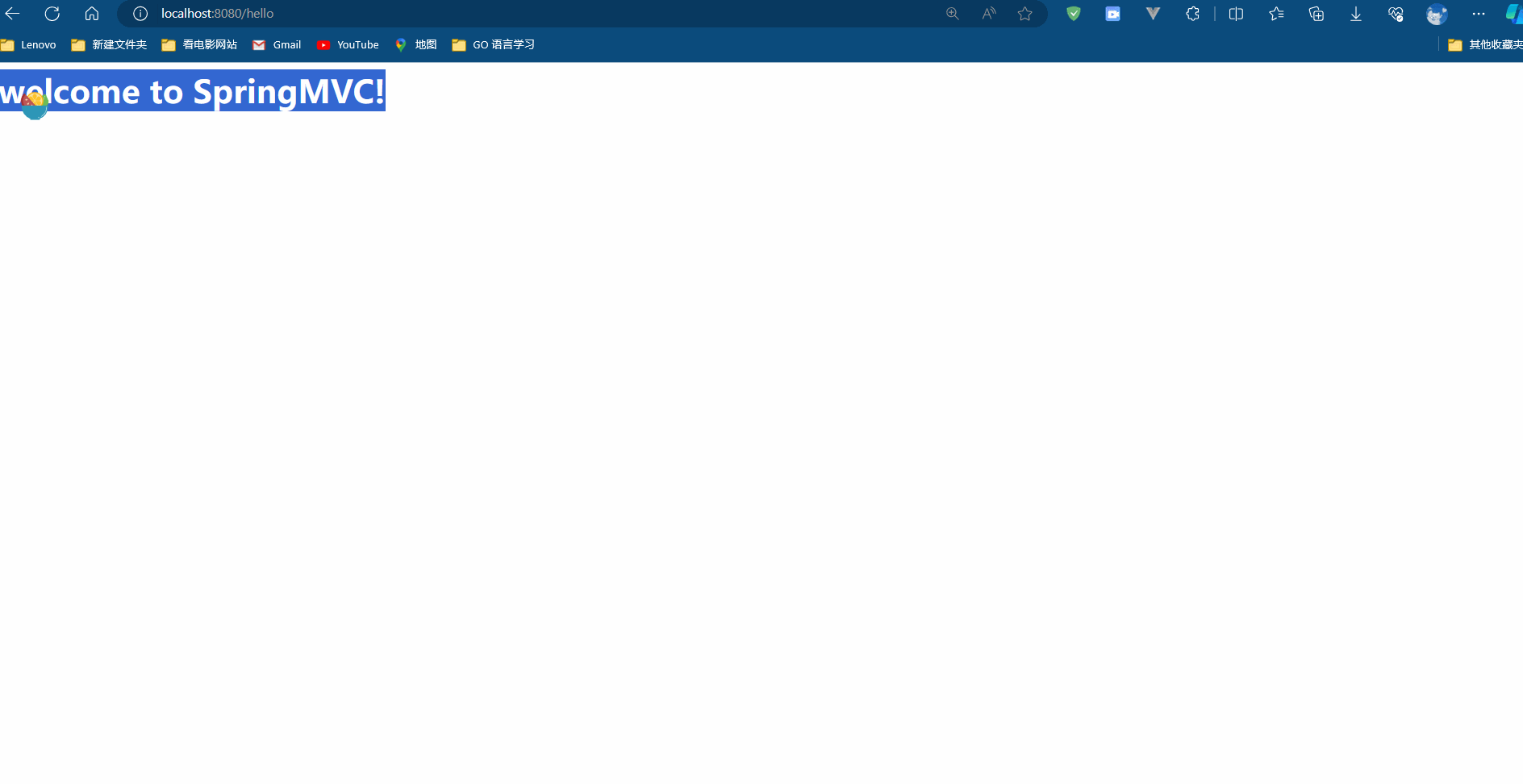
SpringMVC Day 01:入门案例
前言 在我们的日常工作和学习中,Web 开发是一个无法回避的重要环节。而在 Java Web 开发领域,SpringMVC 无疑是一个重量级选手。它以其灵活性、强大功能和清晰的 MVC 结构,赢得了大量开发者的青睐。但是,对于初学者来说ÿ…...
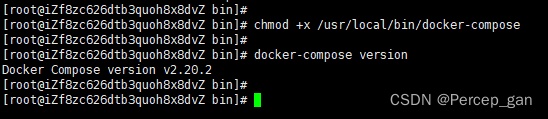
docker、docker-compose安装教程,很详细
docker、docker-compose安装教程,很详细 一、卸载旧版1、查看有没有安装过旧版2、停止docker3、删除安装过docker的相关包4、删除docker相关的镜像和容器 二、docker安装1、设置阿里云镜像2、查看所有docker3、安装最新版本4、安装指定版本 三、使用前准备1、启动do…...

源代码转换:Tangible Software Solutions 23.10 Crack
Tangible Software Solutions The Most Accurate and Reliable Source Code Converters Convert between C#, Java, C, Python, & VB, while saving countless hours of painstaking work and valuable time.源代码转换 Key Benefits Saves valuable time Accurate and com…...

SAD notes
ESKF 总结 prediction 更新误差先验 F F F通过3.42来算 得到 这里有点绕的一点是: 误差状态的 F F F牵涉到名义状态, 而名义状态又需要在时间上推进更新 其中, F中的名义状态的推进通过公式3.41得到, (名义状态不考虑误差, 这一点从3.41d, 3.41e可以看出, 误差状态只考虑…...

[SQL开发笔记]BETWEEN操作符:选取介于两个值之间的数据范围内的值
一、功能描述: BETWEEN操作符:选取介于两个值之间的数据范围内的值。这些值可以是数值、文本或者日期。 二、BETWEEN操作符语法详解: BETWEEN操作符语法: SELECT column1, column2,…FROM table_nameWHERE column BETWEEN val…...

Babylonjs学习笔记(三)——创建天空盒
书接上回,这里讨论创建天空盒!!! // 天空盒const envTex CubeTexture.CreateFromPrefilteredData(./env/environmentSpecular.env,scene)scene.environmentTexture envTex;scene.createDefaultSkybox(envTex,true)scene.environ…...

【计算机网络】文件传输协议FTP和SFTP
1. 介绍 SFTP(SSH文件传输协议)和FTP(文件传输协议)都是用于在计算机之间传输文件的网络协议。FTP和SFTP都位于OSI模型中的应用层。这两种协议用于文件传输和管理,是应用层协议,因此它们工作在OSI模型的最…...

Python 编程语言的介绍
Python 是一种高级、动态类型的解释型语言。由 Guido van Rossum 于1989年底发明,并在1991年首次发布。Python 的设计哲学强调代码的可读性和简洁的语法,特别是使用缩进来表示代码块,这使得开发者能够用更少的代码表达想法。 基础概念: 语法…...
centos服务器搭建安装Gitlab教程使用教程
1、更新服务器: sudo yum update -y && sudo yum upgrade -y 2、下载Gitlab的RPM包 https://packages.gitlab.com/gitlab/gitlab-cece表示开源el表示centos 选64位el8对应CentOS8 本教程以centos8为例,在服务器中,下载centos8的…...

linux复习笔记02(小滴课堂)
linux下输入输出错误重定向: 输入重定向:< 一个大于号是进行了覆盖。 两个大于号是追加。 输出重定向可以用于以后日志打印。 错误重定向: 错误重定向是不把信息打印到屏幕上而是打印到指定文件中去: 输出重定向其实是用的1…...

AWVS漏洞扫描使用基础与介绍
漏洞扫描的基本概念和原理 漏洞扫描是指通过使用自动化工具和技术来检测和识别计算机系统和网络中可能存在的安全漏洞,用于帮助网络安全运维人员及时获取网络安全态势。漏洞扫描是网络安全中的重要环节,它可以帮助我们发现和修复网络中的安全漏洞&#x…...

Flink 维表关联
1、实时查询维表 实时查询维表是指用户在 Flink 算子中直接访问外部数据库,比如用 MySQL 来进行关联,这种方式是同步方式,数据保证是最新的。但是,当我们的流计算数据过大,会对外 部系统带来巨大的访问压力࿰…...

阳光蟹场小程序的盈利模式与思考深度
随着移动互联网的快速发展,小程序成为了各行各业进行数字化转型的重要工具之一。阳光蟹场小程序作为一款专为蟹场管理和销售提供支持的移动,其盈利模式也备受关注。本文将从阳光蟹场小程序的盈利途径、商业模式和对蟹场管理的影响等方面,深入…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
