SAD notes
ESKF 总结
prediction
更新误差先验

F F F通过3.42来算
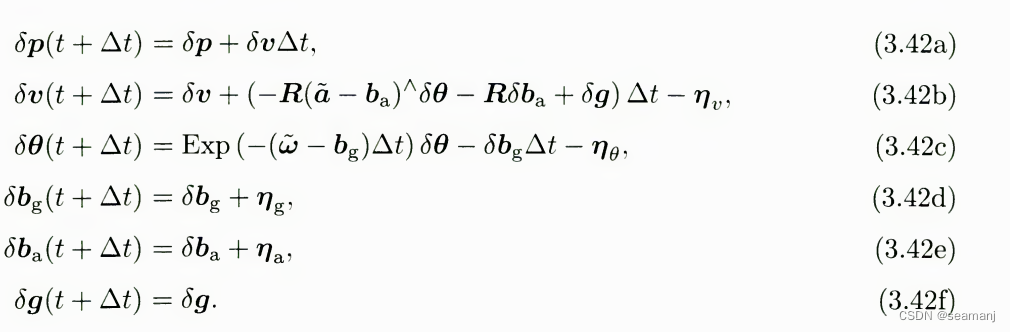
得到
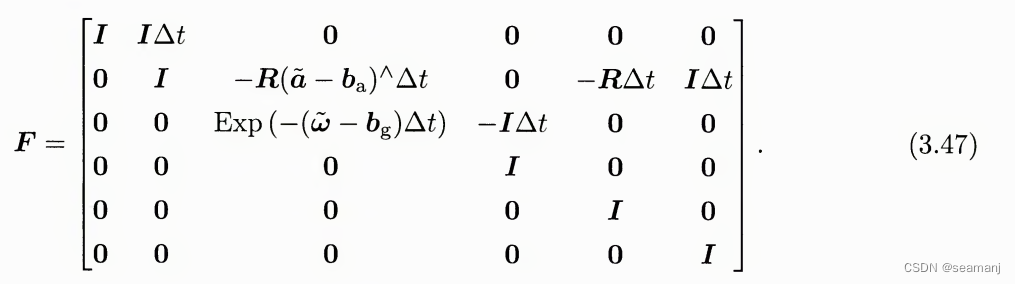
这里有点绕的一点是: 误差状态的 F F F牵涉到名义状态, 而名义状态又需要在时间上推进更新
其中, F中的名义状态的推进通过公式3.41得到,
(名义状态不考虑误差, 这一点从3.41d, 3.41e可以看出, 误差状态只考虑误差, 真实状态为名义+误差)
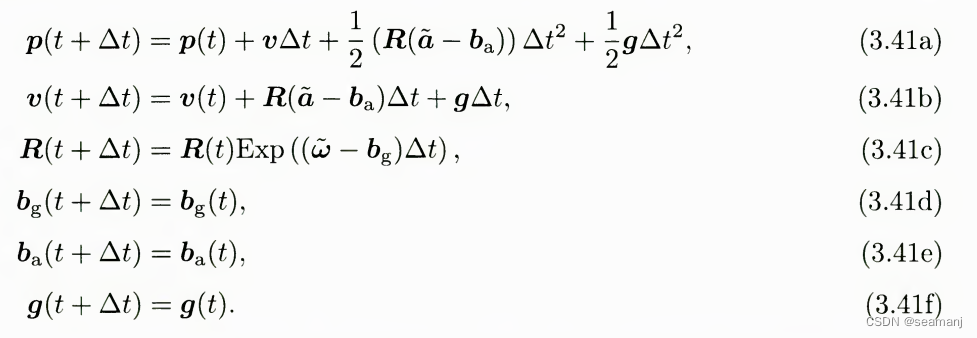 代码的实现
代码的实现
template <typename S>
bool ESKF<S>::Predict(const IMU& imu) {assert(imu.timestamp_ >= current_time_);double dt = imu.timestamp_ - current_time_;if (dt > (5 * options_.imu_dt_) || dt < 0) {// 时间间隔不对,可能是第一个IMU数据,没有历史信息LOG(INFO) << "skip this imu because dt_ = " << dt;current_time_ = imu.timestamp_;return false;}// nominal state 递推VecT new_p = p_ + v_ * dt + 0.5 * (R_ * (imu.acce_ - ba_)) * dt * dt + 0.5 * g_ * dt * dt;VecT new_v = v_ + R_ * (imu.acce_ - ba_) * dt + g_ * dt;SO3 new_R = R_ * SO3::exp((imu.gyro_ - bg_) * dt);R_ = new_R;v_ = new_v;p_ = new_p;// 其余状态维度不变// error state 递推// 计算运动过程雅可比矩阵 F,见(3.47)// F实际上是稀疏矩阵,也可以不用矩阵形式进行相乘而是写成散装形式,这里为了教学方便,使用矩阵形式Mat18T F = Mat18T::Identity(); // 主对角线F.template block<3, 3>(0, 3) = Mat3T::Identity() * dt; // p 对 vF.template block<3, 3>(3, 6) = -R_.matrix() * SO3::hat(imu.acce_ - ba_) * dt; // v对thetaF.template block<3, 3>(3, 12) = -R_.matrix() * dt; // v 对 baF.template block<3, 3>(3, 15) = Mat3T::Identity() * dt; // v 对 gF.template block<3, 3>(6, 6) = SO3::exp(-(imu.gyro_ - bg_) * dt).matrix(); // theta 对 thetaF.template block<3, 3>(6, 9) = -Mat3T::Identity() * dt; // theta 对 bg// mean and cov predictiondx_ = F * dx_; // 这行其实没必要算,dx_在重置之后应该为零,因此这步可以跳过,但F需要参与Cov部分计算,所以保留cov_ = F * cov_.eval() * F.transpose() + Q_; current_time_ = imu.timestamp_;return true;
}
Q Q Q的算法
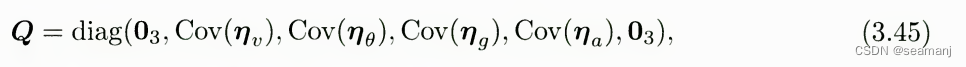
注意, 在离散情况下
η v = η a Δ t η θ = η g Δ t η g = η b g Δ t η a = η b a Δ t \begin{aligned} &\eta_v = \eta_a \Delta t\\ &\eta_ \theta = \eta_g \Delta t \\ &\eta_g = \eta_{bg} \Delta t\\ &\eta_ a = \eta_{ba} \Delta t \\ \end{aligned} ηv=ηaΔtηθ=ηgΔtηg=ηbgΔtηa=ηbaΔt
可以根据3.40将3.42进行一阶泰勒展开
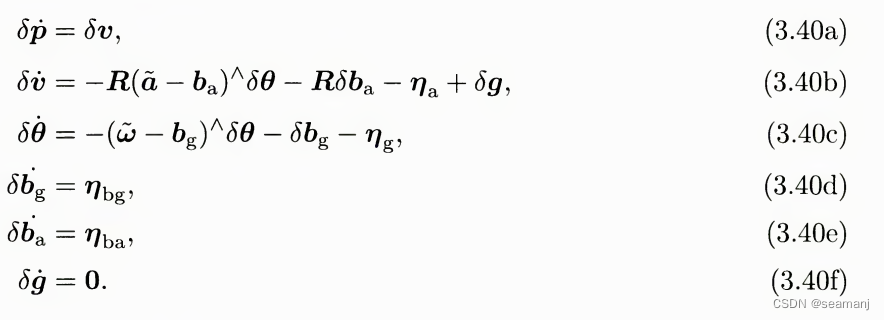
代码中的实现
double ev = options.acce_var_;double et = options.gyro_var_;double eg = options.bias_gyro_var_;double ea = options.bias_acce_var_;double ev2 = ev; // * ev; // tj : 为什么没平方? Q里面应该是方差double et2 = et; // * et;double eg2 = eg; // * eg;double ea2 = ea; // * ea;// 设置过程噪声Q_.diagonal() << 0, 0, 0, ev2, ev2, ev2, et2, et2, et2, eg2, eg2, eg2, ea2, ea2, ea2, 0, 0, 0;
其中options的定义
struct Options {Options() = default;/// IMU 测量与零偏参数double imu_dt_ = 0.01; // IMU测量间隔// NOTE IMU噪声项都为离散时间,不需要再乘dt,可以由初始化器指定IMU噪声double gyro_var_ = 1e-5; // 陀螺测量标准差double acce_var_ = 1e-2; // 加计测量标准差double bias_gyro_var_ = 1e-6; // 陀螺零偏游走标准差double bias_acce_var_ = 1e-4; // 加计零偏游走标准差
correction
更新误差后验
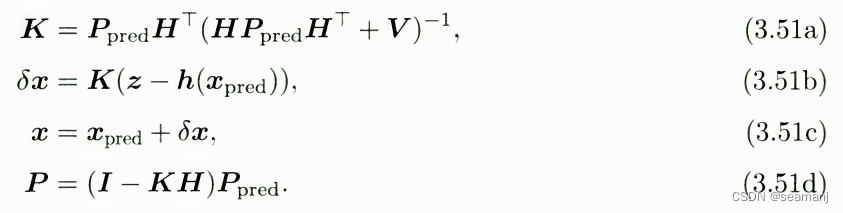
H H H是观测值对误差状态变量的jacob
先看GNSS, 它观测值有位移和旋转, 根据3.66和3.70可得 H H H,

GNSS对旋转的观测是总体的旋转, 然而名义上的 R R R是知道的, 所以我们可以将观测值变以成对于旋转误差状态的直接观测, 这样一来, 它对自己求导就为 I I I
同理, GNSS对位移的观测是总体的位移, 然后名义上的 p p p是知道, 所以我们将对总体位移的观测转到对于误差位移的直接观测
Eigen::Matrix<S, 6, 18> H = Eigen::Matrix<S, 6, 18>::Zero();H.template block<3, 3>(0, 0) = Mat3T::Identity(); // P部分 (3.70)H.template block<3, 3>(3, 6) = Mat3T::Identity(); // R部分(3.66)
然后求 V V V
// 卡尔曼增益和更新过程Vec6d noise_vec;noise_vec << trans_noise, trans_noise, trans_noise, ang_noise, ang_noise, ang_noise;Mat6d V = noise_vec.asDiagonal();
其中trans_noise, ang_noise在option中定义
/// RTK 观测参数double gnss_pos_noise_ = 0.1; // GNSS位置噪声double gnss_height_noise_ = 0.1; // GNSS高度噪声double gnss_ang_noise_ = 1.0 * math::kDEG2RAD; // GNSS旋转噪声
然后更新后验3.51b, 3.51d
// 更新x和covVec6d innov = Vec6d::Zero();innov.template head<3>() = (pose.translation() - p_); // 平移部分innov.template tail<3>() = (R_.inverse() * pose.so3()).log(); // 旋转部分(3.67)dx_ = K * innov;cov_ = (Mat18T::Identity() - K * H) * cov_;
有了误差状态, 就可以更新名义状态3.51c
/// 更新名义状态变量,重置error statevoid UpdateAndReset() {p_ += dx_.template block<3, 1>(0, 0);v_ += dx_.template block<3, 1>(3, 0);R_ = R_ * SO3::exp(dx_.template block<3, 1>(6, 0));if (options_.update_bias_gyro_) {bg_ += dx_.template block<3, 1>(9, 0);}if (options_.update_bias_acce_) {ba_ += dx_.template block<3, 1>(12, 0);}g_ += dx_.template block<3, 1>(15, 0);ProjectCov();dx_.setZero();}
注意 这里有一步需要投影, 参考3.63

/// 对P阵进行投影,参考式(3.63)
void ProjectCov() {Mat18T J = Mat18T::Identity();J.template block<3, 3>(6, 6) = Mat3T::Identity() - 0.5 * SO3::hat(dx_.template block<3, 1>(6, 0));cov_ = J * cov_ * J.transpose();
}
再看odom, 它观测值只有速度
首先求H, 注意这里观测值为本地速度, 但是名义变量 R R R这时是知道的, 所以可以把观测值从本地速度转化到世界速度, 然后世界速度对世界速度求导就为 I I I

// odom 修正以及雅可比
// 使用三维的轮速观测,H为3x18,大部分为零
Eigen::Matrix<S, 3, 18> H = Eigen::Matrix<S, 3, 18>::Zero();
H.template block<3, 3>(0, 3) = Mat3T::Identity();
然后算V
// 设置里程计噪声
double o2 = options_.odom_var_ * options_.odom_var_;
odom_noise_.diagonal() << o2, o2, o2;
option里面的定义
/// 里程计参数
double odom_var_ = 0.5;
double odom_span_ = 0.1; // 里程计测量间隔
double wheel_radius_ = 0.155; // 轮子半径
double circle_pulse_ = 1024.0; // 编码器每圈脉冲数
然后更新后验
本地速度观测值的算法参见 3.76
// velocity obs
double velo_l = options_.wheel_radius_ * odom.left_pulse_ / options_.circle_pulse_ * 2 * M_PI / options_.odom_span_;
double velo_r =options_.wheel_radius_ * odom.right_pulse_ / options_.circle_pulse_ * 2 * M_PI / options_.odom_span_;
double average_vel = 0.5 * (velo_l + velo_r);VecT vel_odom(average_vel, 0.0, 0.0);
VecT vel_world = R_ * vel_odom;dx_ = K * (vel_world - v_);// update cov
cov_ = (Mat18T::Identity() - K * H) * cov_;
UpdateAndReset();
相关文章:

SAD notes
ESKF 总结 prediction 更新误差先验 F F F通过3.42来算 得到 这里有点绕的一点是: 误差状态的 F F F牵涉到名义状态, 而名义状态又需要在时间上推进更新 其中, F中的名义状态的推进通过公式3.41得到, (名义状态不考虑误差, 这一点从3.41d, 3.41e可以看出, 误差状态只考虑…...

[SQL开发笔记]BETWEEN操作符:选取介于两个值之间的数据范围内的值
一、功能描述: BETWEEN操作符:选取介于两个值之间的数据范围内的值。这些值可以是数值、文本或者日期。 二、BETWEEN操作符语法详解: BETWEEN操作符语法: SELECT column1, column2,…FROM table_nameWHERE column BETWEEN val…...

Babylonjs学习笔记(三)——创建天空盒
书接上回,这里讨论创建天空盒!!! // 天空盒const envTex CubeTexture.CreateFromPrefilteredData(./env/environmentSpecular.env,scene)scene.environmentTexture envTex;scene.createDefaultSkybox(envTex,true)scene.environ…...

【计算机网络】文件传输协议FTP和SFTP
1. 介绍 SFTP(SSH文件传输协议)和FTP(文件传输协议)都是用于在计算机之间传输文件的网络协议。FTP和SFTP都位于OSI模型中的应用层。这两种协议用于文件传输和管理,是应用层协议,因此它们工作在OSI模型的最…...

Python 编程语言的介绍
Python 是一种高级、动态类型的解释型语言。由 Guido van Rossum 于1989年底发明,并在1991年首次发布。Python 的设计哲学强调代码的可读性和简洁的语法,特别是使用缩进来表示代码块,这使得开发者能够用更少的代码表达想法。 基础概念: 语法…...
centos服务器搭建安装Gitlab教程使用教程
1、更新服务器: sudo yum update -y && sudo yum upgrade -y 2、下载Gitlab的RPM包 https://packages.gitlab.com/gitlab/gitlab-cece表示开源el表示centos 选64位el8对应CentOS8 本教程以centos8为例,在服务器中,下载centos8的…...

linux复习笔记02(小滴课堂)
linux下输入输出错误重定向: 输入重定向:< 一个大于号是进行了覆盖。 两个大于号是追加。 输出重定向可以用于以后日志打印。 错误重定向: 错误重定向是不把信息打印到屏幕上而是打印到指定文件中去: 输出重定向其实是用的1…...

AWVS漏洞扫描使用基础与介绍
漏洞扫描的基本概念和原理 漏洞扫描是指通过使用自动化工具和技术来检测和识别计算机系统和网络中可能存在的安全漏洞,用于帮助网络安全运维人员及时获取网络安全态势。漏洞扫描是网络安全中的重要环节,它可以帮助我们发现和修复网络中的安全漏洞&#x…...

Flink 维表关联
1、实时查询维表 实时查询维表是指用户在 Flink 算子中直接访问外部数据库,比如用 MySQL 来进行关联,这种方式是同步方式,数据保证是最新的。但是,当我们的流计算数据过大,会对外 部系统带来巨大的访问压力࿰…...

阳光蟹场小程序的盈利模式与思考深度
随着移动互联网的快速发展,小程序成为了各行各业进行数字化转型的重要工具之一。阳光蟹场小程序作为一款专为蟹场管理和销售提供支持的移动,其盈利模式也备受关注。本文将从阳光蟹场小程序的盈利途径、商业模式和对蟹场管理的影响等方面,深入…...

2-Java进阶知识总结-7-UDP-TCP
文章目录 网络编程概述网络编程三要素--IP地址IP地址--概念(IP:Internet Protocol)IP地址--分类IP地址--特殊的地址:127.0.0.1IP地址获取--DOS命令IP地址获取--InetAddress类 网络编程三要素--端口端口--概念端口号 网络编程三要素…...
C++数据结构X篇_19_排序基本概念及冒泡排序(重点是核心代码,冒泡是稳定的排序)
文章目录 1. 排序基本概念2. 冒泡排序2.1 核心代码2.2 冒泡排序代码2.3 查看冒泡排序的时间消耗2.4 冒泡排序改进版减小时间消耗 1. 排序基本概念 现实生活中排序很重要,例如:淘宝按条件搜索的结果展示等。 概念 排序是计算机内经常进行的一种操作,其目…...
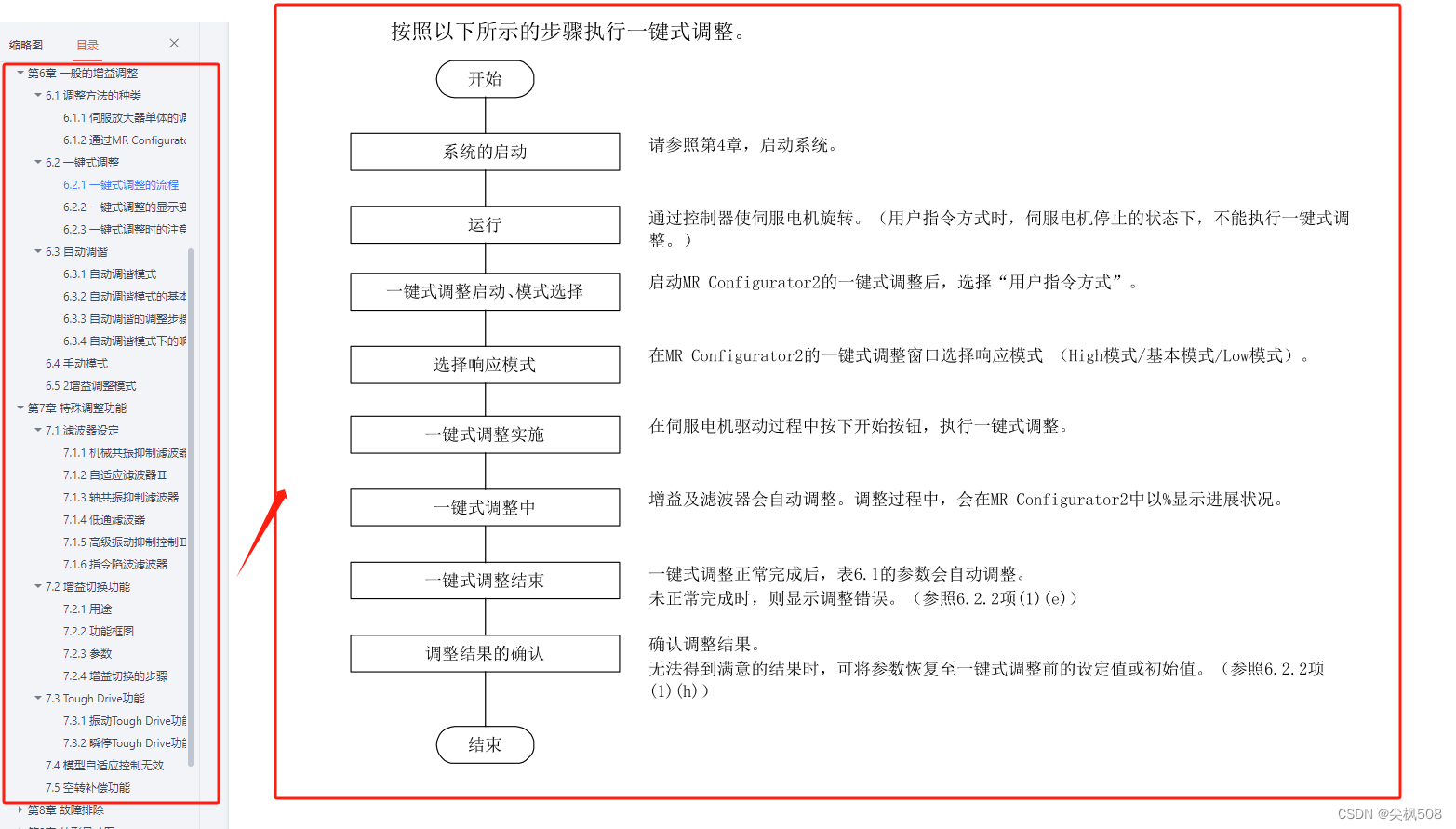
工作:三菱伺服驱动器连接参数及其电机钢性参数配置与调整
工作:三菱伺服驱动器参数及电机钢性参数配置与调整 一、三菱PLC与伺服驱动器连接参数的设置 1. 伺服配置 单个JET伺服从站链接侧占用点数:Rx/Ry占用64点、RWw/RWr占用32点 图中配置了22个JET伺服从站,占用点数:Rx/Ry占用64222048点、RWw/RWr占用322…...
企事业单位/公司电脑文件透明加密保护 | 防泄密软件\系统!
推荐——「天锐绿盾电脑文件防泄密系统」 一款全面的企业/公司数据透明加密防泄密系统,旨在从源头上保障数据的安全和使用安全。 PC访问地址: https://isite.baidu.com/site/wjz012xr/2eae091d-1b97-4276-90bc-6757c5dfedee 它具有以下特点:…...
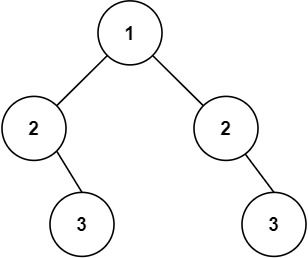
[Leetcode] 0101. 对称二叉树
101. 对称二叉树 题目描述 给你一个二叉树的根节点 root , 检查它是否轴对称。 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true示例 2: 输入:root [1,2,2,null,3,null,3] 输出:false提示&#…...
.NET、VUE利用RSA加密完成登录并且发放JWT令牌设置权限访问
后端生成公钥私钥 使用RSA.ToXmlString(Boolean) 方法生成公钥以及私钥。 RSACryptoServiceProvider rSA new(); string pubKey rSA.ToXmlString(false);//公钥 string priKey rSA.ToXmlString(true);//私钥 后端将生成的公钥发送给前端 创建一个get请求,将…...

go实现文件的读写
读文件 1.ioutil.ReadFile package mainimport ("fmt""io/ioutil" )func main() {filePath : "example.txt"data, err : ioutil.ReadFile(filePath)if err ! nil {fmt.Printf("无法读取文件:%v\n", err)return}fmt.Print…...
基于 nodejs+vue购物网站设计系统mysql
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
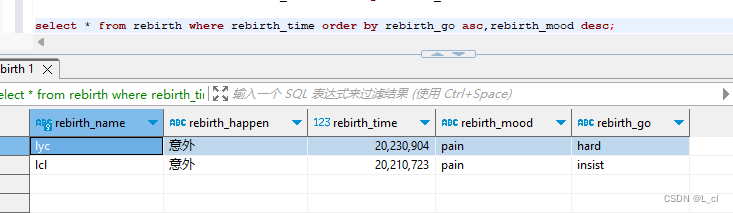
Mysql数据库 4.SQL语言 DQL数据操纵语言 查询
DQL数据查询语言 从数据表中提取满足特定条件的记录 1.单表查询 2.多表查询 查询基础语法 select 关键字后指定要查询到的记录的哪些列 语法:select 列名(字段名)/某几列/全部列 from 表名 [具体条件]; select colnumName…...

threejs(3)-详解材质与纹理
一、Matcap(MeshMatcapMaterial)材质原理与应用 Matcap是一张含有光照信息的贴图,通常是直接截取材质球截图来使用。因此Matcap可以很好的模拟静止光源下的光照效果。 最直接的方式就是直接使用在View空间下的模型法向量的xy分量去采样Matcap。 另外还有一种常见…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
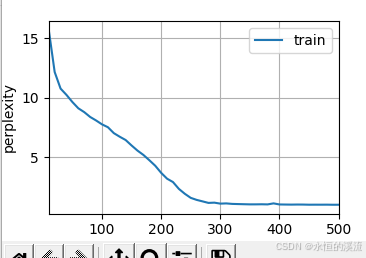
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...
