KF-GINS 和 OB-GINS 的 Earth类 和 Rotation 类
原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning
文章目录
- 一、Earth 类:地球参数和坐标转换
- 1、gravity():正常重力计算
- 2、meridianPrimeVerticalRadius():计算子午圈半径 RM、卯酉圈半径 RN
- 3、RN():计算卯酉圈主半径 RN
- 4、cne():n系(导航坐标系)到e系(地心地固坐标系)转换矩阵
- 5、qne():计算n系(北东地)到e系(ECEF)转换四元数
- 6、blh():从n系到e系转换四元数得到纬度和经度
- 7、blh2ecef():大地坐标(经纬高)转地心地固坐标
- 7、ecef2blh():地心地固坐标转大地坐标
- 8、DRi(): 计算 n 系相对位置转大地坐标相对位置的矩阵
- 9、DR():计算大地坐标相对位置转 n 系相对位置的矩阵
- 10、local2global():局部坐标(在origin处展开)转大地坐标
- 11、global2local():大地坐标转局部坐标(在origin处展开)
- 12、iewe():地球自转角速度投影到e系
- 13、iewn():地球自转角速度投影到n系
- 14、enwn():n系相对于e系转动角速度投影到n系
- 二、Rotation 类:姿态转换
- 1、matrix2quaternion():旋转矩阵转四元数
- 2、quaternion2matrix():四元数转旋转矩阵
- 3、matrix2euler():旋转矩阵转欧拉角
- 4、quaternion2euler():四元数转欧拉角
- 5、rotvec2quaternion():等效旋转矢量转四元数
- 6、quaternion2vector():四元数转旋转矢量
- 7、euler2matrix():欧拉角转旋转矩阵
- 8、euler2quaternion():欧拉角转四元数
- 9、skewSymmetric():计算三维向量反对称阵
- 10、quaternionleft()、quaternionright():四元数矩阵
一、Earth 类:地球参数和坐标转换

Earth 类里都是静态函数,使用的时候直接类名::成员函数(),文件的开头定义了一些椭球参数:
/* WGS84椭球模型参数NOTE:如果使用其他椭球模型需要修改椭球参数 */
const double WGS84_WIE = 7.2921151467E-5; /* 地球自转角速度*/
const double WGS84_F = 0.0033528106647474805; /* 扁率 */
const double WGS84_RA = 6378137.0000000000; /* 长半轴a */
const double WGS84_RB = 6356752.3142451793; /* 短半轴b */
const double WGS84_GM0 = 398600441800000.00; /* 地球引力常数 */
const double WGS84_E1 = 0.0066943799901413156; /* 第一偏心率平方 */
const double WGS84_E2 = 0.0067394967422764341; /* 第二偏心率平方 */
1、gravity():正常重力计算
重力是万有引力与离心力共同作用的结果,随纬度升高离心力增大但引力减小、随高程升高引力减小,共同作用下重力的计算公式如下:
g L = 9.7803267715 × ( 1 + 0.0052790414 × sin 2 L − 0.0000232718 × sin 2 2 L ) + h × ( 0.0000000043977311 × sin 2 L − 0.0000030876910891 ) + 0.0000000000007211 × sin 4 2 L g_{L}=9.7803267715 \times\left(1+0.0052790414 \times \sin ^{2} L-0.0000232718 \times \sin ^{2} 2 L\right) \\ +h\times(0.0000000043977311\times\sin ^{2} L-0.0000030876910891)+0.0000000000007211\times\sin ^{4} 2 L gL=9.7803267715×(1+0.0052790414×sin2L−0.0000232718×sin22L)+h×(0.0000000043977311×sin2L−0.0000030876910891)+0.0000000000007211×sin42L
static double gravity(const Vector3d &blh) {double sin2 = sin(blh[0]);sin2 *= sin2;return 9.7803267715 * (1 + 0.0052790414 * sin2 + 0.0000232718 * sin2 * sin2) +blh[2] * (0.0000000043977311 * sin2 - 0.0000030876910891) + 0.0000000000007211 * blh[2] * blh[2];
}
2、meridianPrimeVerticalRadius():计算子午圈半径 RM、卯酉圈半径 RN
返回值是 Vector2d,第一个是子午圈主曲率半径 RM、第二个是卯酉圈主半径 RN:
R M = R e ( 1 − e 2 ) ( 1 − e 2 sin 2 L ) 3 / 2 、 R N = R e 1 − e 2 sin 2 L R_{M}=\frac{R_{e}\left(1-e^{2}\right)}{\left(1-e^{2} \sin ^{2} L\right)^{3 / 2}}、R_{N}=\frac{R_{e}}{\sqrt{1-e^{2} \sin ^{2} L}} RM=(1−e2sin2L)3/2Re(1−e2)、RN=1−e2sin2LRe
static Eigen::Vector2d meridianPrimeVerticalRadius(double lat) {double tmp, sqrttmp;tmp = sin(lat); tmp *= tmp;tmp = 1 - WGS84_E1 * tmp;sqrttmp = sqrt(tmp);return {WGS84_RA * (1 - WGS84_E1) / (sqrttmp * tmp), WGS84_RA / sqrttmp};
}
3、RN():计算卯酉圈主半径 RN
R N = R e 1 − e 2 sin 2 L R_{N}=\frac{R_{e}}{\sqrt{1-e^{2} \sin ^{2} L}} RN=1−e2sin2LRe
static double RN(double lat) {double sinlat = sin(lat);return WGS84_RA / sqrt(1.0 - WGS84_E1 * sinlat * sinlat);
}
4、cne():n系(导航坐标系)到e系(地心地固坐标系)转换矩阵
C e n = [ − sin φ 0 cos φ 0 1 0 − cos φ 0 − sin φ ] [ cos λ sin λ 0 − sin λ cos λ 0 0 0 1 ] = [ − sin φ cos λ − sin φ sin λ cos φ − sin λ cos λ 0 − cos φ cos λ − cos φ sin λ − sin φ ] C_{e}^{n}=\left[\begin{array}{ccc}-\sin \varphi & 0 & \cos \varphi \\ 0 & 1 & 0 \\ -\cos \varphi & 0 & -\sin \varphi\end{array}\right]\left[\begin{array}{ccc}\cos \lambda & \sin \lambda & 0 \\ -\sin \lambda & \cos \lambda & 0 \\ 0 & 0 & 1\end{array}\right]=\\ \left[\begin{array}{ccc}-\sin \varphi \cos \lambda & -\sin \varphi \sin \lambda & \cos \varphi \\ -\sin \lambda & \cos \lambda & 0 \\ -\cos \varphi \cos \lambda & -\cos \varphi \sin \lambda & -\sin \varphi\end{array}\right] Cen= −sinφ0−cosφ010cosφ0−sinφ cosλ−sinλ0sinλcosλ0001 = −sinφcosλ−sinλ−cosφcosλ−sinφsinλcosλ−cosφsinλcosφ0−sinφ
static Matrix3d cne(const Vector3d &blh) {double coslon, sinlon, coslat, sinlat;sinlat = sin(blh[0]);sinlon = sin(blh[1]);coslat = cos(blh[0]);coslon = cos(blh[1]);Matrix3d dcm;dcm(0, 0) = -sinlat * coslon;dcm(0, 1) = -sinlon;dcm(0, 2) = -coslat * coslon;dcm(1, 0) = -sinlat * sinlon;dcm(1, 1) = coslon;dcm(1, 2) = -coslat * sinlon;dcm(2, 0) = coslat;dcm(2, 1) = 0;dcm(2, 2) = -sinlat;return dcm;
}
5、qne():计算n系(北东地)到e系(ECEF)转换四元数
位置更新的时候,调用此函数根据上一时刻经纬度,得到上一时刻的 qne,然后 qee * qne * qnn 得到当前时刻的 qne,再调用下面的 blh() 得到经纬度。
q n e = [ cos ( − π / 4 − φ / 2 ) cos ( λ / 2 ) − sin ( − π / 4 − φ / 2 ) sin ( λ / 2 ) sin ( − π / 4 − φ / 2 ) cos ( λ / 2 ) cos ( − π / 4 − sin / 2 ) sin ( λ / 2 ) ] ] \boldsymbol{q}_{n}^{e}=\left[\begin{array}{c}\cos (-\pi / 4-\varphi / 2) \cos (\lambda / 2) \\ -\sin (-\pi / 4-\varphi / 2) \sin (\lambda / 2) \\ \sin (-\pi / 4-\varphi / 2) \cos (\lambda / 2) \\ \cos (-\pi / 4-\sin / 2) \sin (\lambda / 2)]\end{array}\right] qne= cos(−π/4−φ/2)cos(λ/2)−sin(−π/4−φ/2)sin(λ/2)sin(−π/4−φ/2)cos(λ/2)cos(−π/4−sin/2)sin(λ/2)]
/* n系(导航坐标系)到e系(地心地固坐标系)转换四元数 */
static Quaterniond qne(const Vector3d &blh) {Quaterniond quat;double coslon, sinlon, coslat, sinlat;coslon = cos(blh[1] * 0.5);sinlon = sin(blh[1] * 0.5);coslat = cos(-M_PI * 0.25 - blh[0] * 0.5);sinlat = sin(-M_PI * 0.25 - blh[0] * 0.5);quat.w() = coslat * coslon;quat.x() = -sinlat * sinlon;quat.y() = sinlat * coslon;quat.z() = coslat * sinlon;return quat;
}
6、blh():从n系到e系转换四元数得到纬度和经度
位置更新的时候,通过算当前时刻 n 系到 e 系转换四元数 qne,然后调用此函数得到经纬度。
/* 从n系到e系转换四元数得到纬度和经度 */
static Vector3d blh(const Quaterniond &qne, double height) {return {-2 * atan(qne.y() / qne.w()) - M_PI * 0.5, 2 * atan2(qne.z(), qne.w()), height};
}
7、blh2ecef():大地坐标(经纬高)转地心地固坐标
x = ( R N + h ) cos L cos λ y = ( R N + h ) cos L sin λ z = [ R N ( 1 − e 2 ) + h ] sin L \begin{array}{l}x=\left(R_{N}+h\right) \cos L \cos \lambda \\ y=\left(R_{N}+h\right) \cos L \sin \lambda \\ z=\left[R_{N}\left(1-e^{2}\right)+h\right] \sin L\end{array} x=(RN+h)cosLcosλy=(RN+h)cosLsinλz=[RN(1−e2)+h]sinL
/* 大地坐标(纬度、经度和高程)转地心地固坐标 */
static Vector3d blh2ecef(const Vector3d &blh) {double coslat, sinlat, coslon, sinlon;double rnh, rn;coslat = cos(blh[0]);sinlat = sin(blh[0]);coslon = cos(blh[1]);sinlon = sin(blh[1]);rn = RN(blh[0]);rnh = rn + blh[2];return {rnh * coslat * coslon, rnh * coslat * sinlon, (rnh - rn * WGS84_E1) * sinlat};
}
7、ecef2blh():地心地固坐标转大地坐标
B 0 = arctan ( Z ( 1 − e 2 ) p ) N k = a 1 − e 2 sin 2 B k − 1 H k = p cos B k − 1 − N k B k = arctan ( z ( 1 − e 2 N k N k ) p ) \begin{array}{c}B_{0}=\arctan \left(\frac{Z}{\left(1-e^{2}\right) p}\right) \\ N_{k}=\frac{a}{\sqrt{1-e^{2} \sin ^{2} B_{k-1}}} \\ H_{k}=\frac{p}{\cos B_{k-1}}-N_{k} \\ B_{k}=\arctan \left(\frac{z}{\left(1-\frac{e^{2} N_{k}}{N_{k}}\right)\ p }\right)\end{array} B0=arctan((1−e2)pZ)Nk=1−e2sin2Bk−1aHk=cosBk−1p−NkBk=arctan (1−Nke2Nk) pz
static Vector3d ecef2blh(const Vector3d &ecef) {double p = sqrt(ecef[0] * ecef[0] + ecef[1] * ecef[1]);double rn;double lat, lon;double h = 0, h2;// 初始状态lat = atan(ecef[2] / (p * (1.0 - WGS84_E1)));lon = 2.0 * atan2(ecef[1], ecef[0] + p);do {h2 = h;rn = RN(lat);h = p / cos(lat) - rn;lat = atan(ecef[2] / (p * (1.0 - WGS84_E1 * rn / (rn + h))));} while (fabs(h - h2) > 1.0e-4);return {lat, lon, h};
}
8、DRi(): 计算 n 系相对位置转大地坐标相对位置的矩阵
通过算出来的矩阵实现 ENU 和 LLH 之间的转换:
- 捷联惯导求出的速度是 n 系的,要转成经纬度增量就得用这个矩阵。
- 杆臂误差补偿时也需要用这个函数,因为杆臂是 n 系的,算出的 IMU 坐标和给的 GNSS 解都是经纬高。
- 存的位置是经纬高,GNSS 量测更新时候计算的是 ENU 下位置的增量,反馈的时候也需要此矩阵。
[ δ φ δ L δ H ] = [ ( R M + H ) − 1 0 0 0 ( R N + H ) − 1 0 0 0 − 1 ] [ δ p N δ p E δ p B ] \left[\begin{array}{l}\delta \varphi \\ \delta L \\ \delta H\end{array}\right]=\left[\begin{array}{ccc}\left(R_{M}+H\right)^{-1} & 0 & 0 \\ 0 & \left(R_{N}+H\right)^{-1} & 0 \\ 0 & 0 & -1 \end{array}\right]\left[\begin{array}{l}\delta \boldsymbol{p}_{N} \\ \delta \boldsymbol{p}_{E} \\ \delta \boldsymbol{p}_{B}\end{array}\right] δφδLδH = (RM+H)−1000(RN+H)−1000−1 δpNδpEδpB
/* n系相对位置转大地坐标相对位置 */
static Matrix3d DRi(const Vector3d &blh) {Matrix3d dri = Matrix3d::Zero();Eigen::Vector2d rmn = meridianPrimeVerticalRadius(blh[0]);dri(0, 0) = 1.0 / (rmn[0] + blh[2]);dri(1, 1) = 1.0 / ((rmn[1] + blh[2]) * cos(blh[0]));dri(2, 2) = -1;return dri;
}
9、DR():计算大地坐标相对位置转 n 系相对位置的矩阵
就是上面 DRI() 计算矩阵的倒数。
[ δ φ δ L δ H ] = [ ( R M + H ) 0 0 0 ( R N + H ) 0 0 0 − 1 ] [ δ p N δ p E δ p B ] \left[\begin{array}{l}\delta \varphi \\ \delta L \\ \delta H\end{array}\right]=\left[\begin{array}{ccc}\left(R_{M}+H\right) & 0 & 0 \\ 0 & \left(R_{N}+H\right) & 0 \\ 0 & 0 & -1 \end{array}\right]\left[\begin{array}{l}\delta \boldsymbol{p}_{N} \\ \delta \boldsymbol{p}_{E} \\ \delta \boldsymbol{p}_{B}\end{array}\right] δφδLδH = (RM+H)000(RN+H)000−1 δpNδpEδpB
/* 大地坐标相对位置转n系相对位置 */
static Matrix3d DR(const Vector3d &blh) {Matrix3d dr = Matrix3d::Zero();Eigen::Vector2d rmn = meridianPrimeVerticalRadius(blh[0]);dr(0, 0) = rmn[0] + blh[2];dr(1, 1) = (rmn[1] + blh[2]) * cos(blh[0]);dr(2, 2) = -1;return dr;
}
10、local2global():局部坐标(在origin处展开)转大地坐标
在 enwn() 中被调用,为了方便能直接传入北东地(n 系)坐标计算 n 系相对于 e 系转动角速度在 n 系的投影。
static Vector3d local2global(const Vector3d &origin, const Vector3d &local) {Vector3d ecef0 = blh2ecef(origin);Matrix3d cn0e = cne(origin);Vector3d ecef1 = ecef0 + cn0e * local;Vector3d blh1 = ecef2blh(ecef1);return blh1;
}
11、global2local():大地坐标转局部坐标(在origin处展开)
好像整个程序中都没用到这个函数。
static Vector3d global2local(const Vector3d &origin, const Vector3d &global) {Vector3d ecef0 = blh2ecef(origin);Matrix3d cn0e = cne(origin);Vector3d ecef1 = blh2ecef(global);return cn0e.transpose() * (ecef1 - ecef0);
}
static Pose global2local(const Vector3d &origin, const Pose &global) {Pose local;Vector3d ecef0 = blh2ecef(origin);Matrix3d cn0e = cne(origin);Vector3d ecef1 = blh2ecef(global.t);Matrix3d cn1e = cne(global.t);local.t = cn0e.transpose() * (ecef1 - ecef0);local.R = cn0e.transpose() * cn1e * global.R;return local;
}
12、iewe():地球自转角速度投影到e系
ω i e e = [ 0 0 ω e ] T \boldsymbol{\omega}_{i e}^{e}=\left[\begin{array}{lll}0 & 0 & \omega_{e}\end{array}\right]^{T} ωiee=[00ωe]T
static Vector3d iewe() {return {0, 0, WGS84_WIE};
}
13、iewn():地球自转角速度投影到n系
ω i e n = [ ω e cos φ 0 − ω e sin φ ] T \boldsymbol{\omega}_{i e}^{n}=\left[\begin{array}{lll}\omega_{e} \cos \varphi & 0 & -\omega_{e} \sin \varphi\end{array}\right]^{T} ωien=[ωecosφ0−ωesinφ]T
static Vector3d iewn(double lat) {return {WGS84_WIE * cos(lat), 0, -WGS84_WIE * sin(lat)};
}
也可以直接传入北东地(n 系)坐标计算:
static Vector3d iewn(const Vector3d &origin, const Vector3d &local) {Vector3d global = local2global(origin, local);return iewn(global[0]);
}
14、enwn():n系相对于e系转动角速度投影到n系
由载体运动线速度和地球曲率引起,与东向、北向速度有关,与天向速度无关
ω e n n = [ v E R N + h − v N R M + h − v E tan φ R N + h ] T \boldsymbol{\omega}_{e n}^{n}=\left[\begin{array}{lll}\frac{v_{E}}{R_{N}+h} & \frac{-v_{N}}{R_{M}+h} & -\frac{v_{E} \tan \varphi}{R_{N}+h}\end{array}\right]^{T} ωenn=[RN+hvERM+h−vN−RN+hvEtanφ]T
static Vector3d enwn(const Eigen::Vector2d &rmn, const Vector3d &blh, const Vector3d &vel) {return {vel[1] / (rmn[1] + blh[2]), -vel[0] / (rmn[0] + blh[2]), -vel[1] * tan(blh[0]) / (rmn[1] + blh[2])};
}
同样也可以直接传入北东地(n 系)坐标计算:
static Vector3d enwn(const Vector3d &origin, const Vector3d &local, const Vector3d &vel) {Vector3d global = local2global(origin, local);Eigen::Vector2d rmn = meridianPrimeVerticalRadius(global[0]);return enwn(rmn, global, vel);
}
二、Rotation 类:姿态转换

1、matrix2quaternion():旋转矩阵转四元数
Eigen 中的四元数可以直接传入旋转矩阵(三维矩阵)构造:
static Quaterniond matrix2quaternion(const Matrix3d &matrix) {return Quaterniond(matrix);
}
2、quaternion2matrix():四元数转旋转矩阵
四元数调用 toRotationMatrix() 函数,转为旋转矩阵:
static Matrix3d quaternion2matrix(const Quaterniond &quaternion) {return quaternion.toRotationMatrix();
}
3、matrix2euler():旋转矩阵转欧拉角
ZYX 旋转顺序,前右下的 IMU,输出 RPY:
static Vector3d matrix2euler(const Eigen::Matrix3d &dcm) {Vector3d euler;euler[1] = atan(-dcm(2, 0) / sqrt(dcm(2, 1) * dcm(2, 1) + dcm(2, 2) * dcm(2, 2)));if (dcm(2, 0) <= -0.999) {euler[0] = atan2(dcm(2, 1), dcm(2, 2));euler[2] = atan2((dcm(1, 2) - dcm(0, 1)), (dcm(0, 2) + dcm(1, 1)));} else if (dcm(2, 0) >= 0.999) {euler[0] = atan2(dcm(2, 1), dcm(2, 2));euler[2] = M_PI + atan2((dcm(1, 2) + dcm(0, 1)), (dcm(0, 2) - dcm(1, 1)));} else {euler[0] = atan2(dcm(2, 1), dcm(2, 2));euler[2] = atan2(dcm(1, 0), dcm(0, 0));}// heading 0~2PIif (euler[2] < 0) {euler[2] = M_PI * 2 + euler[2];}return euler;
}
4、quaternion2euler():四元数转欧拉角
先调用 toRotationMatrix() 转为旋转矩阵,再调用 matrix2euler() 转欧拉角:
static Vector3d quaternion2euler(const Quaterniond &quaternion) {return matrix2euler(quaternion.toRotationMatrix());
}
5、rotvec2quaternion():等效旋转矢量转四元数
根据传入的旋转矢量,计算向量的长度作为旋转的角度,计算向量的归一化版本作为旋转的轴,然后调用 AngleAxisd(),将角度和轴转换为四元数。
static Quaterniond rotvec2quaternion(const Vector3d &rotvec) {double angle = rotvec.norm(); // 计算向量的长度作为旋转的角度Vector3d vec = rotvec.normalized(); // 计算向量的归一化版本作为旋转的轴return Quaterniond(Eigen::AngleAxisd(angle, vec)); // 调用 AngleAxisd(),将角度和轴转换为四元数
}
6、quaternion2vector():四元数转旋转矢量
传入的四元数通过 Eigen::AngleAxisd 类的构造函数转换为角度轴(angle-axis)表示。角度轴是一个描述旋转的方法,其中旋转角度和旋转轴是两个独立的部分。然后,该函数返回这个角度轴表示的旋转的角度乘以旋转的轴,得到一个三维向量。这个向量的 x、y 和 z 分量分别对应于旋转轴在x、y 和 z 轴上的分量,而其长度(或者说范数)等于旋转角度。
static Vector3d quaternion2vector(const Quaterniond &quaternion) {Eigen::AngleAxisd axisd(quaternion);return axisd.angle() * axisd.axis();
}
7、euler2matrix():欧拉角转旋转矩阵
三个欧拉角分别转为 ZYX 角轴,相乘之后构造旋转矩阵
static Matrix3d euler2matrix(const Vector3d &euler) {return Matrix3d(Eigen::AngleAxisd(euler[2], Vector3d::UnitZ()) *Eigen::AngleAxisd(euler[1], Vector3d::UnitY()) *Eigen::AngleAxisd(euler[0], Vector3d::UnitX()));
}
8、euler2quaternion():欧拉角转四元数
三个欧拉角分别转为 ZYX 角轴,相乘之后构造四元数
static Quaterniond euler2quaternion(const Vector3d &euler) {return Quaterniond(Eigen::AngleAxisd(euler[2], Vector3d::UnitZ()) *Eigen::AngleAxisd(euler[1], Vector3d::UnitY()) *Eigen::AngleAxisd(euler[0], Vector3d::UnitX()));
}
9、skewSymmetric():计算三维向量反对称阵
static Matrix3d skewSymmetric(const Vector3d &vector) {Matrix3d mat;mat << 0, -vector(2), vector(1), vector(2), 0, -vector(0), -vector(1), vector(0), 0;return mat;
}
10、quaternionleft()、quaternionright():四元数矩阵
P ∘ Q = [ p 0 − p 1 − p 2 − p 3 p 1 p 0 − p 3 p 2 p 2 p 3 p 0 − p 1 p 3 − p 2 p 1 p 0 ] [ q 0 q 1 q 2 q 3 ] = M P Q = [ q 0 − q 1 − q 2 − q 3 q 1 q 0 q 3 − q 2 q 2 − q 3 q 0 q 1 q 3 q 2 − q 1 q 0 ] [ p 0 p 1 p 2 p 3 ] = M Q ′ P \boldsymbol{P} \circ \boldsymbol{Q}=\left[\begin{array}{cccc}p_{0} & -p_{1} & -p_{2} & -p_{3} \\ p_{1} & p_{0} & -p_{3} & p_{2} \\ p_{2} & p_{3} & p_{0} & -p_{1} \\ p_{3} & -p_{2} & p_{1} & p_{0}\end{array}\right]\left[\begin{array}{l}q_{0} \\ q_{1} \\ q_{2} \\ q_{3}\end{array}\right]=\boldsymbol{M}_{P} \boldsymbol{Q}=\left[\begin{array}{cccc}q_{0} & -q_{1} & -q_{2} & -q_{3} \\ q_{1} & q_{0} & q_{3} & -q_{2} \\ q_{2} & -q_{3} & q_{0} & q_{1} \\ q_{3} & q_{2} & -q_{1} & q_{0}\end{array}\right]\left[\begin{array}{l}p_{0} \\ p_{1} \\ p_{2} \\ p_{3}\end{array}\right]=\boldsymbol{M}_{Q}^{\prime} \boldsymbol{P} P∘Q= p0p1p2p3−p1p0p3−p2−p2−p3p0p1−p3p2−p1p0 q0q1q2q3 =MPQ= q0q1q2q3−q1q0−q3q2−q2q3q0−q1−q3−q2q1q0 p0p1p2p3 =MQ′P
M P = [ p 0 − p 1 − p 2 − p 3 p 1 p 0 − p 3 p 2 p 2 p 3 p 0 − p 1 p 3 − p 2 p 1 p 0 ] = [ p 0 − p v T p v p 0 I + ( p v × ) ] \boldsymbol{M}_{P}=\left[\begin{array}{cccc}p_{0} & -p_{1} & -p_{2} & -p_{3} \\ p_{1} & p_{0} & -p_{3} & p_{2} \\ p_{2} & p_{3} & p_{0} & -p_{1} \\ p_{3} & -p_{2} & p_{1} & p_{0}\end{array}\right]=\left[\begin{array}{cc}p_{0} & -\boldsymbol{p}_{v}^{\mathrm{T}} \\ \boldsymbol{p}_{v} & p_{0} \boldsymbol{I}+\left(\boldsymbol{p}_{v} \times\right)\end{array}\right] MP= p0p1p2p3−p1p0p3−p2−p2−p3p0p1−p3p2−p1p0 =[p0pv−pvTp0I+(pv×)]
static Eigen::Matrix4d quaternionleft(const Quaterniond &q) {Eigen::Matrix4d ans;ans(0, 0) = q.w();ans.block<1, 3>(0, 1) = -q.vec().transpose();ans.block<3, 1>(1, 0) = q.vec();ans.block<3, 3>(1, 1) = q.w() * Eigen::Matrix3d::Identity() + skewSymmetric(q.vec());return ans;
}
M Q ′ = [ q 0 − q 1 − q 2 − q 3 q 1 q 0 q 3 − q 2 q 2 − q 3 q 0 q 1 q 3 q 2 − q 1 q 0 ] = [ q 0 − q v T q v q 0 I − ( q v × ) ] \boldsymbol{M}_{Q}^{\prime}=\left[\begin{array}{cccc}q_{0} & -q_{1} & -q_{2} & -q_{3} \\ q_{1} & q_{0} & q_{3} & -q_{2} \\ q_{2} & -q_{3} & q_{0} & q_{1} \\ q_{3} & q_{2} & -q_{1} & q_{0}\end{array}\right]=\left[\begin{array}{cc}q_{0} & -\boldsymbol{q}_{v}^{\mathrm{T}} \\ \boldsymbol{q}_{v} & q_{0} \boldsymbol{I}-\left(\boldsymbol{q}_{v} \times\right)\end{array}\right] MQ′= q0q1q2q3−q1q0−q3q2−q2q3q0−q1−q3−q2q1q0 =[q0qv−qvTq0I−(qv×)]
static Eigen::Matrix4d quaternionright(const Quaterniond &p) {Eigen::Matrix4d ans;ans(0, 0) = p.w();ans.block<1, 3>(0, 1) = -p.vec().transpose();ans.block<3, 1>(1, 0) = p.vec();ans.block<3, 3>(1, 1) = p.w() * Eigen::Matrix3d::Identity() - skewSymmetric(p.vec());return ans;
}
egin{array}{cc}q_{0} & -\boldsymbol{q}{v}^{\mathrm{T}} \ \boldsymbol{q}{v} & q_{0} \boldsymbol{I}-\left(\boldsymbol{q}_{v} \times\right)\end{array}\right]
$$
static Eigen::Matrix4d quaternionright(const Quaterniond &p) {Eigen::Matrix4d ans;ans(0, 0) = p.w();ans.block<1, 3>(0, 1) = -p.vec().transpose();ans.block<3, 1>(1, 0) = p.vec();ans.block<3, 3>(1, 1) = p.w() * Eigen::Matrix3d::Identity() - skewSymmetric(p.vec());return ans;
}
相关文章:

KF-GINS 和 OB-GINS 的 Earth类 和 Rotation 类
原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning 文章目录 一、Earth 类:地球参数和坐标转换1、gravity():正常重力计算2、meridianPrimeVerticalRadius():计算子午圈半径…...

2017年亚太杯APMCM数学建模大赛B题喷雾轨迹规划问题求解全过程文档及程序
2017年亚太杯APMCM数学建模大赛 B题 喷雾轨迹规划问题 原题再现 喷釉工艺用喷釉枪或喷釉机在压缩空气下将釉喷入雾中,使釉附着在泥体上。这是陶瓷生产过程中一个容易实现自动化的过程。由于不均匀的釉料在烧制过程中会产生裂纹,导致工件报废࿰…...

柏拉图式爱情是同性之爱,绘画是理念世界的二次模仿
公元前427年,柏拉图出生在雅典。 柏拉图20岁成为苏格拉底的弟子。 有一次,柏拉图问苏格拉底:“什么是爱情?”苏格拉底说:“请穿越麦田,摘一株最大最金黄的麦穗回来。不走回头路,只能摘一次。”…...

【滴滴出行安全应急响应平台DSRC2倍积分卡】
1、使用方法 2、券(记得点个关注,做一下数据)...

HashMap 元素添加流程
在Java 1.8中,HashMap的元素添加流程: 计算键的哈希值:当调用put(key, value)方法时,首先会计算键(key)的哈希值,这个哈希值用来确定元素在内部数组中的位置。确定位置:通过哈希值&…...

甲亢_甲状腺功能亢进_Methimazole甲巯基咪唑
美国医生 Methimazole甲巯基咪唑 is used to treat hyperthyroidism, a condition where the thyroid gland produces too much thyroid hormone. It is also used before thyroid surgery or radioactive iodine treatment. Methimazole is an antithyroid medicine. It wor…...
【Maven】VSCode Java+Maven 环境配置
0x00 前言 没写过 Java,得配个带 Maven 的编码环境,不太明白,试试看顺便记录一下 0x01 配置过程 安装 jdk1.8 后,找到安装位置: (base) dianCD-Ali doraemon % /usr/libexec/java_home -V Matching Java Virtual Ma…...

【目标检测】非极大值抑制NMS的原理与实现
非极大值抑制(Non-Maximum Suppression,NMS)是目标检测中常用的一种技术,它的主要作用是去除冗余和重叠过高的框,并保留最佳的几个。 NMS计算的具体步骤如下: 首先根据目标检测模型输出结果,得…...

应用程序架构是如何演变的
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 如果您一直在开发或以某种方式参与应用程序架构,那么在过去的几年中您肯定看到了许多变化。有很多不同类型的架构和技术陆续出现然后消失,以至于…...

云原生Docker Cgroups资源控制操作
目录 资源控制 cgroups四大功能 CPU 资源控制 设置CPU使用率上限 进行CPU压力测试 设置50%的比例分配CPU使用时间上限 设置CPU资源占用比(设置多个容器时才有效) 设置容器绑定指定的CPU 对内存使用的限制 限制容器可以使用的最大内存 限制可用的…...

【Java集合类面试二十五】、有哪些线程安全的List?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:有哪些线程安全的List&a…...
分布式系统的链路追踪,让你轻松解决订单无法查看的问题!
你好,我是积极活泼的小米!今天我要跟大家聊聊分布式系统的链路追踪,这个话题对于我们在技术领域工作的小伙伴们来说,可是非常重要的哦! 背景 昨天,产品大佬丰哥找到了我,他抱怨说分销员的订单…...

基于生产数据测试设计、测试回归
问题背景 QA搬砖日常中,你会不会有这样的问题,测试设计时有些场景没考虑到,上线就因为测试中没覆盖到的场景而导致缺陷溢出。从缺陷分类统计来看,类似这样的例子占比是很高的。 解决措施 仅依靠测试者设置的场景,模拟…...

装了mac os 14.0 sonoma 在腾讯会议投屏时候,无法设置麦克风权限问题
愿意:界面上直接空白的,无法手动或自动弹出要配置授权的软件 解决思路: 给 TCC.db 增加1条权限记录 添加到数据库里 /usr/bin/sqlite3 ~/Library/Application\ Support/com.apple.TCC/TCC.db "INSERT INTO main.access (service, cli…...

ARM 汇编指令 orreq 的使用
orreq 阅读代码时,发现有个【组合指令】 orreq, orr 一般是 OR,也就是或操作,后面加个 eq 表示什么呢? 比如下面的代码:前面一个操作, tst,好像没做实际的操作,可能影响…...
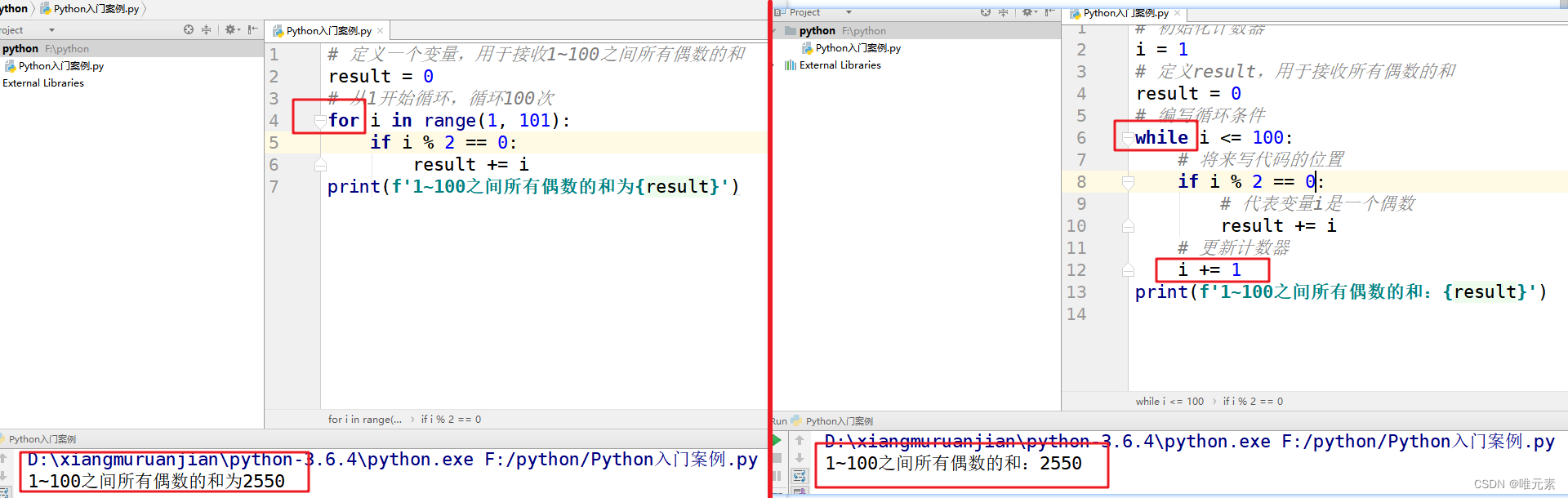
Python---练习:for循环 求1-100的和/所有偶数的和
案例: 使用for循环,求1 ~ 100的和 之前用while循环,做过算出1--100的和。 相关链接: Python--练习:使用while循环求1..100的和-CSDN博客 结合着看看for循环怎么实现。 思考: 先把for循环的基本语法写…...

APP逆向基础(APK流程)
APK的基本结构 Android体系结构和APK基本结构-CSDN博客 APK 打包流程 【Android 安装包优化】APK 打包流程 ( 文件结构 | 打包流程 | 安装流程 | 安卓虚拟机 )_adnroid 安装包优化,打指定资源_韩曙亮的博客-CSDN博客 APK安装流程...

Tomcat调试端口被占用解决办法
Tomcat调试端口被占用解决办法 tomcat启动报错: Unable to open debugger port (127.0.0.1:52718): java.net.BindException "Address already in use: NET_Bind"这个错误表明Tomcat服务器在启动时尝试打开调试端口(通常是在调试模式下使用的…...
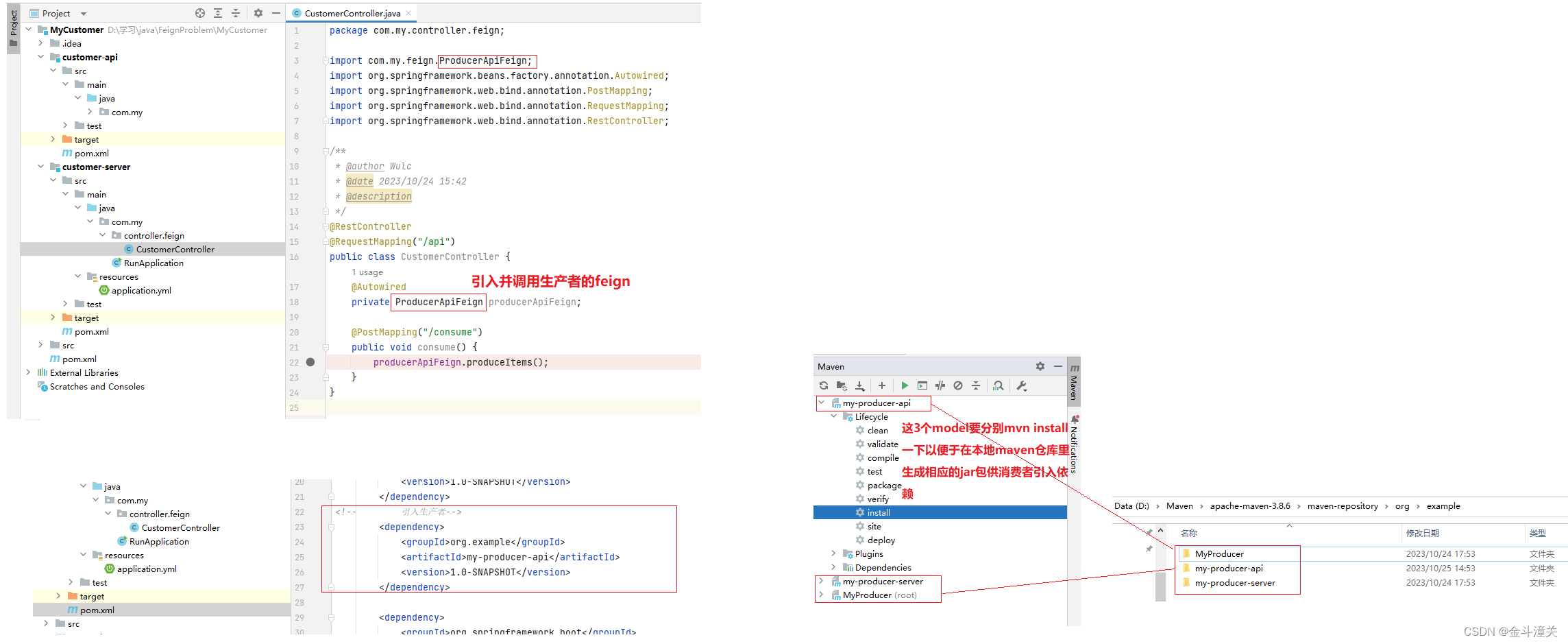
feign之间相互通信RequestInterceptor拦截器失效
1、问题描述 前段时间碰到一个问题,有两个服务A和服务B,通过feign进行通信。因为feign之间无法直接传递请求头,只能传请求体。因此需要借助RequestInterceptor拦截器获取到请求头。服务B中设置了RequestInterceptor拦截器,但是在A…...

GoLong的学习之路(十)语法之函数
书接上回,上回书说到,结构体,一言之重在于体。一体之重在于经。经之重甚于骨。这张就说go的经络—函数。 文章目录 函数函数如何定义参数可变参数 返回值多返回值 函数类型与变量 高阶函数函数作为参数函数作为返回值匿名函数闭包defer语句底…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
