Python机器学习17——Xgboost和Lightgbm结合分位数回归(机器学习与传统统计学结合)
最近XGboost支持分位数回归了,我看了一下,就做了个小的代码案例。毕竟学术市场上做这种新颖的机器学习和传统统计学结合的方法还是不多,算的上创新,找个好数据集可以发论文。
代码实现
导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
import xgboost as xgb
import lightgbm as lgb
import statsmodels.api as sm
from statsmodels.regression.quantile_regression import QuantRegxgboost和lightgbm都需要安装的,他们和sklearn库的机器学习方法不是一个库的。怎么安装看我《实用的机器学习》这个栏目的xgb那篇文章。
模拟数据进行分位数回归
先制作一个模拟数据集
def f(x: np.ndarray) -> np.ndarray:return x * np.sin(x)rng = np.random.RandomState(2023)
X = np.atleast_2d(rng.uniform(0, 10.0, size=1000)).T
expected_y = f(X).ravel()
sigma = 0.5 + X.ravel() / 10.0
noise = rng.lognormal(sigma=sigma) - np.exp(sigma**2.0 / 2.0)
y = expected_y + noiseprint(X.shape,y.shape)
然后画图看看:
plt.figure(figsize=(6,2),dpi=100)
plt.scatter(X,y,s=1)
plt.show()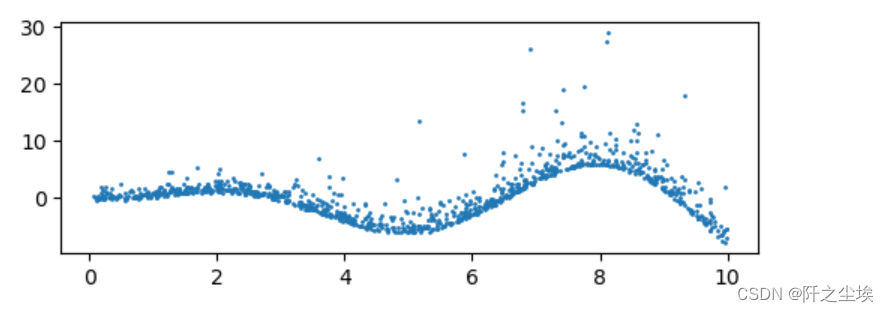
#划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)
print(f"Training data shape: {X_train.shape}, Testing data shape: {X_test.shape}")
这里采用三种模型进行拟合预测对比,分别是线性分位数回归,XGB结合分位数,LightGBM结合分位数:
alphas = np.arange(5, 100, 5) / 100.0
print(alphas)
mse_qr, mse_xgb, mse_lgb = [], [], []
r2_qr, r2_xgb, r2_lgb = [], [], []
qr_pred,xgb_pred,lgb_pred={},{},{}# Train and evaluate
for alpha in alphas:# Quantile Regressionmodel_qr = QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)model_pred=model_qr.predict(sm.add_constant(X_test))mse_qr.append(mean_squared_error(y_test,model_pred ))r2_qr.append(r2_score(y_test,model_pred))# XGBoostmodel_xgb = xgb.train({"objective": "reg:quantileerror", 'quantile_alpha': alpha}, xgb.QuantileDMatrix(X_train, y_train), num_boost_round=100)model_pred=model_xgb.predict(xgb.DMatrix(X_test))mse_xgb.append(mean_squared_error(y_test,model_pred ))r2_xgb.append(r2_score(y_test,model_pred))# LightGBMmodel_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True,}, lgb.Dataset(X_train, y_train), num_boost_round=100)model_pred=model_lgb.predict(X_test)mse_lgb.append(mean_squared_error(y_test,model_pred))r2_lgb.append(r2_score(y_test,model_pred))if alpha in [0.1,0.5,0.9]:qr_pred[alpha]=model_qr.predict(sm.add_constant(X_test))xgb_pred[alpha]=model_xgb.predict(xgb.DMatrix(X_test))lgb_pred[alpha]=model_lgb.predict(X_test)分位点为0.1,0.5,0.9时记录一下,方便画图查看。
然后画出三种模型在不同分位点下的误差和拟合优度对比:
plt.figure(figsize=(7, 5),dpi=128)
plt.subplot(211)
plt.plot(alphas, mse_qr, label='Quantile Regression')
plt.plot(alphas, mse_xgb, label='XGBoost')
plt.plot(alphas, mse_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('MSE')
plt.title('MSE across different quantiles')plt.subplot(212)
plt.plot(alphas, r2_qr, label='Quantile Regression')
plt.plot(alphas, r2_xgb, label='XGBoost')
plt.plot(alphas, r2_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('$R^2$')
plt.title('$R^2$ across different quantiles')
plt.tight_layout()
plt.show()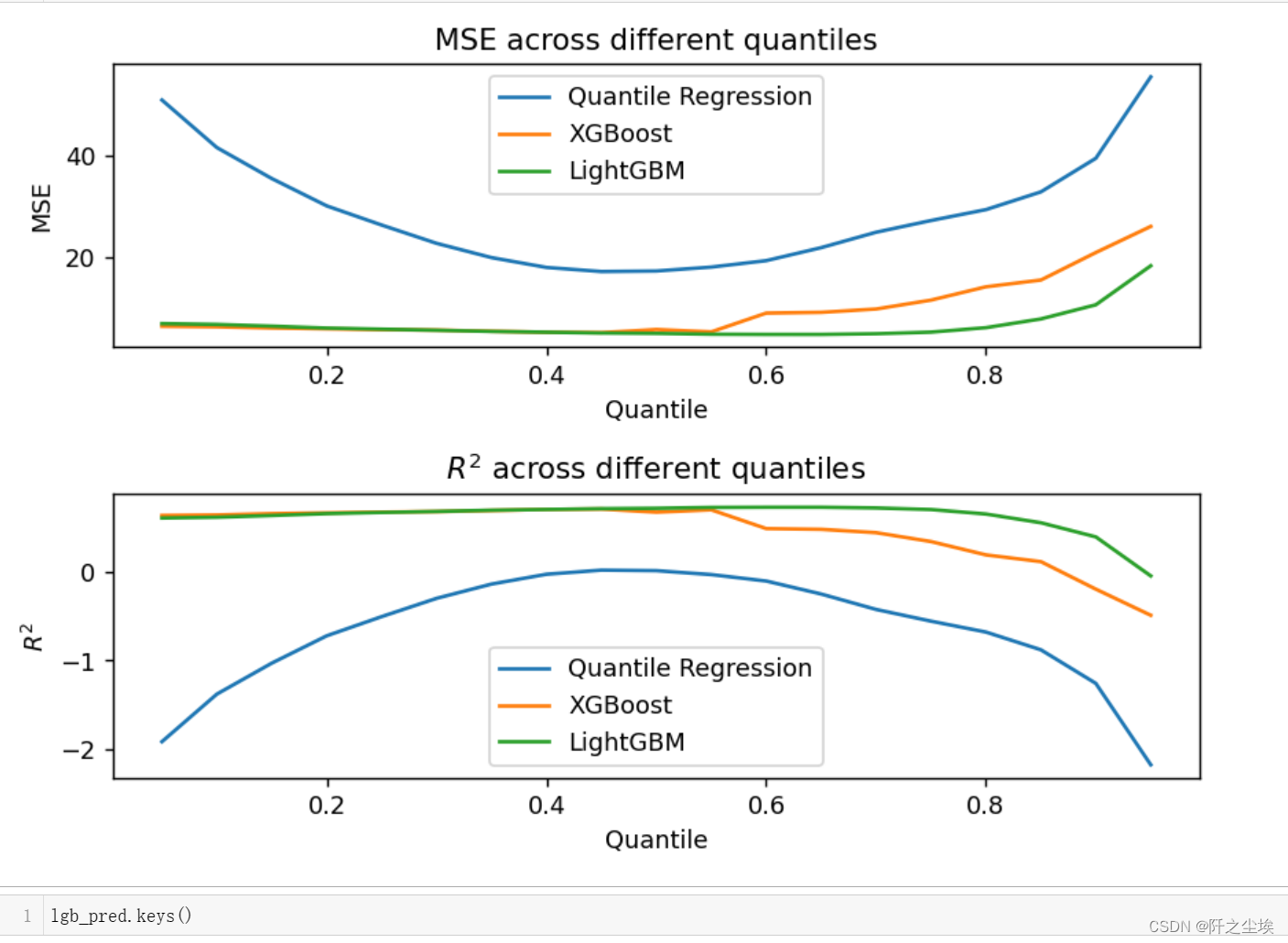
可以看到在分位点为0.5附件,模型的误差都比较小。因为这个数据集没有很多的异常值。然后模型表现上,LGBM>XGB>线性QR。线性模型对于一个非线性的函数关系拟合在这里当然不行。
画出拟合图:
name=['QR','XGB-QR','LGB-QR']
plt.figure(figsize=(7, 6),dpi=128)
for k,model in enumerate([qr_pred,xgb_pred,lgb_pred]):n=int(str('31')+str(k+1))plt.subplot(n)plt.scatter(X_test,y_test,c='k',s=2)for i,alpha in enumerate([0.1,0.5,0.9]):sort_order = np.argsort(X_test, axis=0).ravel()X_test_sorted = np.array(X_test)[sort_order]#print(np.array(model[alpha]))predictions_sorted = np.array(model[alpha])[sort_order]plt.plot(X_test_sorted,predictions_sorted,label=fr"$\tau$={alpha}",lw=0.8)plt.legend()plt.title(f'{name[k]}')
plt.tight_layout()
plt.show()
可以看到分位数回归的明显的区间特点。
还有非参数非线性方法的优势,明显XGB和LGBM拟合得更好。
波士顿数据集
上面是人工数据,下面采用真实的数据集进行对比,就用回归最常用的波士顿房价数据集吧:
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
column_names = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO', 'B','LSTAT', 'MEDV']
boston=pd.DataFrame(np.hstack([data,target.reshape(-1,1)]),columns= column_names)取出X和y,划分测试集和训练集
X = boston.iloc[:,:-1]
y = boston.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)拟合预测,对比
alphas = np.arange(0.1, 1, 0.1)
mse_qr, mse_xgb, mse_lgb = [], [], []
r2_qr, r2_xgb, r2_lgb = [], [], []
qr_pred,xgb_pred,lgb_pred={},{},{}
# Train and evaluate
for alpha in alphas:# Quantile Regressionmodel_qr = QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)model_pred=model_qr.predict(sm.add_constant(X_test))mse_qr.append(mean_squared_error(y_test,model_pred ))r2_qr.append(r2_score(y_test,model_pred))# XGBoostmodel_xgb = xgb.train({"objective": "reg:quantileerror", 'quantile_alpha': alpha}, xgb.QuantileDMatrix(X_train, y_train), num_boost_round=100)model_pred=model_xgb.predict(xgb.DMatrix(X_test))mse_xgb.append(mean_squared_error(y_test,model_pred ))r2_xgb.append(r2_score(y_test,model_pred))# LightGBMmodel_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True,}, lgb.Dataset(X_train, y_train), num_boost_round=100)model_pred=model_lgb.predict(X_test)mse_lgb.append(mean_squared_error(y_test,model_pred))r2_lgb.append(r2_score(y_test,model_pred))if alpha in [0.1,0.5,0.9]:qr_pred[alpha]=model_qr.predict(sm.add_constant(X_test))xgb_pred[alpha]=model_xgb.predict(xgb.DMatrix(X_test))lgb_pred[alpha]=model_lgb.predict(X_test)画图查看不同分位点的不同模型的误差和拟合优度:
plt.figure(figsize=(8, 5),dpi=128)
plt.subplot(211)
plt.plot(alphas, mse_qr, label='Quantile Regression')
plt.plot(alphas, mse_xgb, label='XGBoost')
plt.plot(alphas, mse_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('MSE')
plt.title('MSE across different quantiles')plt.subplot(212)
plt.plot(alphas, r2_qr, label='Quantile Regression')
plt.plot(alphas, r2_xgb, label='XGBoost')
plt.plot(alphas, r2_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('$R^2$')
plt.title('$R^2$ across different quantiles')
plt.tight_layout()
plt.show()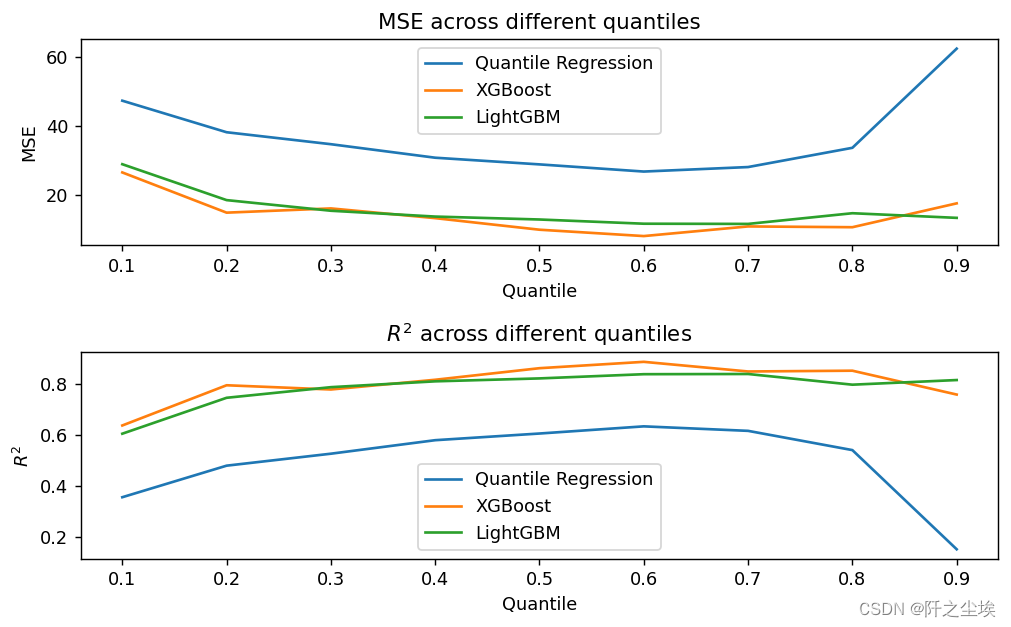
可以看到在分位点为0.6附件三个模型表现效果都比较好,然后模型表现来看,XGB>LGBM>QR,还是两个机器学习模型更厉害。
分位数损失函数和平方和损失函数对比
上面我们得到在分位点为0.6的时候,模型效果表现好,那么分位数模型和普通的MSE损失函数的效果比起来怎么样呢?我们继续对比:
# 定义alpha值
alpha = 0.5# 分位数回归模型
model_qr = sm.regression.quantile_regression.QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)
qr_pred = model_qr.predict(sm.add_constant(X_test))# XGBoost分位数回归
model_xgb = xgb.train({"objective": "reg:quantileerror", 'quantile_alpha': alpha}, xgb.DMatrix(X_train, label=y_train), num_boost_round=100)
xgb_q_pred = model_xgb.predict(xgb.DMatrix(X_test))# LightGBM分位数回归
model_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True}, lgb.Dataset(X_train, label=y_train), num_boost_round=100)
lgb_q_pred = model_lgb.predict(X_test)# 普通的最小二乘法线性回归
model_lr = LinearRegression()
model_lr.fit(X_train, y_train)
lr_pred = model_lr.predict(X_test)# 普通的XGBoost
model_xgb_reg = xgb.train({"objective": "reg:squarederror"}, xgb.DMatrix(X_train, label=y_train), num_boost_round=100)
xgb_pred = model_xgb_reg.predict(xgb.DMatrix(X_test))# 普通的LightGBM
model_lgb_reg = lgb.train({'objective': 'regression', 'force_col_wise': True}, lgb.Dataset(X_train, label=y_train), num_boost_round=100)
lgb_pred = model_lgb_reg.predict(X_test)上面是六个模型,非别是基于分位数回归的XGB,LGBM,线性分位数回归。还有三个基于最普通的MSE损失函数的普通XGB,LGBM和最小二乘线性回归。
# 计算6个模型的MSE和R^2
models = ['QR', 'XGB Quantile', 'LightGBM Quantile', 'Linear Reg', 'XGBoost', 'LightGBM']
preds = [qr_pred, xgb_q_pred, lgb_q_pred, lr_pred, xgb_pred, lgb_pred]
mse_scores = [mean_squared_error(y_test, pred) for pred in preds]
r2_scores = [r2_score(y_test, pred) for pred in preds]画柱状图查看:
colors = sns.color_palette("muted", len(models))
fig, axs = plt.subplots(2, 1, figsize=(9,7))
axs[0].bar(models, mse_scores, color=colors)
axs[0].set_title('MSE Comparison')
axs[0].set_ylabel('MSE')
axs[1].bar(models, r2_scores, color=colors)
axs[1].set_title(r'$R^{2}$ Comparison')
axs[1].set_ylabel(r'$R^{2}$')
plt.tight_layout()
plt.show()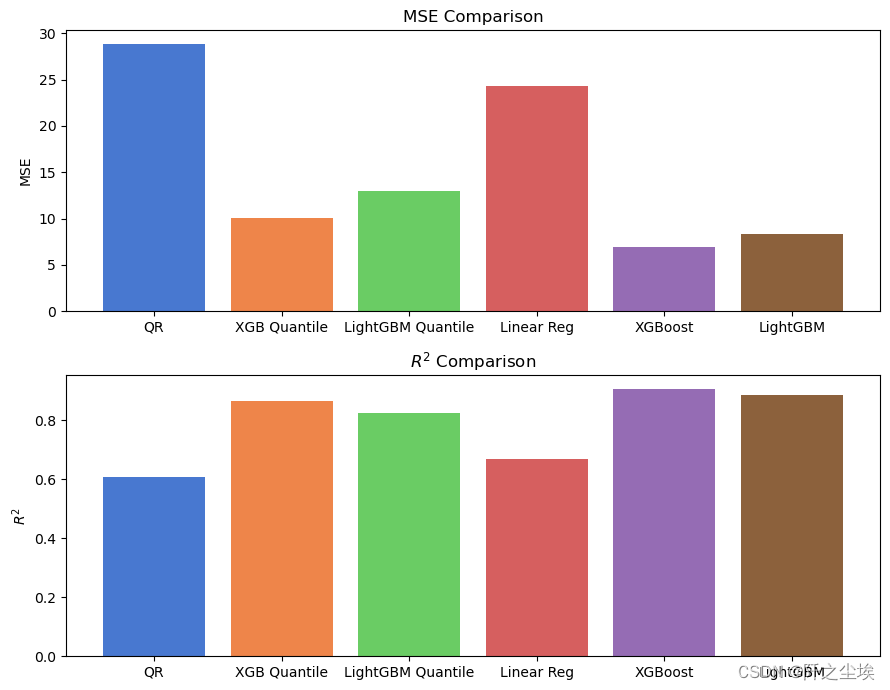
可以看到模型效果来看,XGboost由于Lightgbm优于线性模型。但是分位数回归效果没有MSE损失好,说明在这个数据集表现上,就采用最经典的MSE损失的普通的模型效果会更好。。。
确实是这样的,很多学术创新和改进都不一定比最经典和最常见的方法的效果好。
如果是那种异常值很多的数据,具有异方差的数据 ,可能损失函数改用分位数的会更好。
相关文章:

Python机器学习17——Xgboost和Lightgbm结合分位数回归(机器学习与传统统计学结合)
最近XGboost支持分位数回归了,我看了一下,就做了个小的代码案例。毕竟学术市场上做这种新颖的机器学习和传统统计学结合的方法还是不多,算的上创新,找个好数据集可以发论文。 代码实现 导入包 import numpy as np import pandas…...

C#编程学习
1. **C#简介**: - C#是一种现代的、面向对象的编程语言,由Microsoft开发。 - 它是.NET框架的一部分,用于开发Windows应用程序、Web应用程序和服务等。 2. **开发环境**: - 你可以使用Visual Studio或Visual Studio Code…...
)
关于vue 父级不使用子级某模块 (插槽替换)
父级: <template><div><MoreSupplements code"Xmgk" message"补充内容越多,越精准"><template #r-btn>xxx</template></MoreSupplements></div> </template> <script> import MoreSupplements fr…...

睿趣科技:抖音小店在哪里选品
随着抖音平台的日益火爆,越来越多的商家选择在抖音小店开设自己的店铺。然而,对于许多新手来说,如何选品却成为了一个难题。那么,抖音小店应该在哪里选品呢? 首先,我们可以从抖音平台上的热门商品入手。通过观察抖音上…...

量变引起质变:安卓改多了,就是自己的OS
最近小米也发布了自己的OS,其他也有厂家跟进。这是自华为鸿蒙之后,大家都说自己开发OS。对此,也是有很多争论的。 有人说,这些东西不都是安卓套壳或者改名吗?怎么就变成了自己的OS?这种观点对不对呢&#x…...

IDEA 之 在不更改操作系统用户名的情况下更改 ${USER} 变量?
如何在不更改操作系统用户名的情况下更改 IntelliJ IDEA 中的 ${USER} 变量 IDEA -> Help -> Edit Custom VM 添加如下内容 -Duser.nameusername这样在文件或者函数注释的时候会读取这个配置,而不会读取电脑登录用户名...
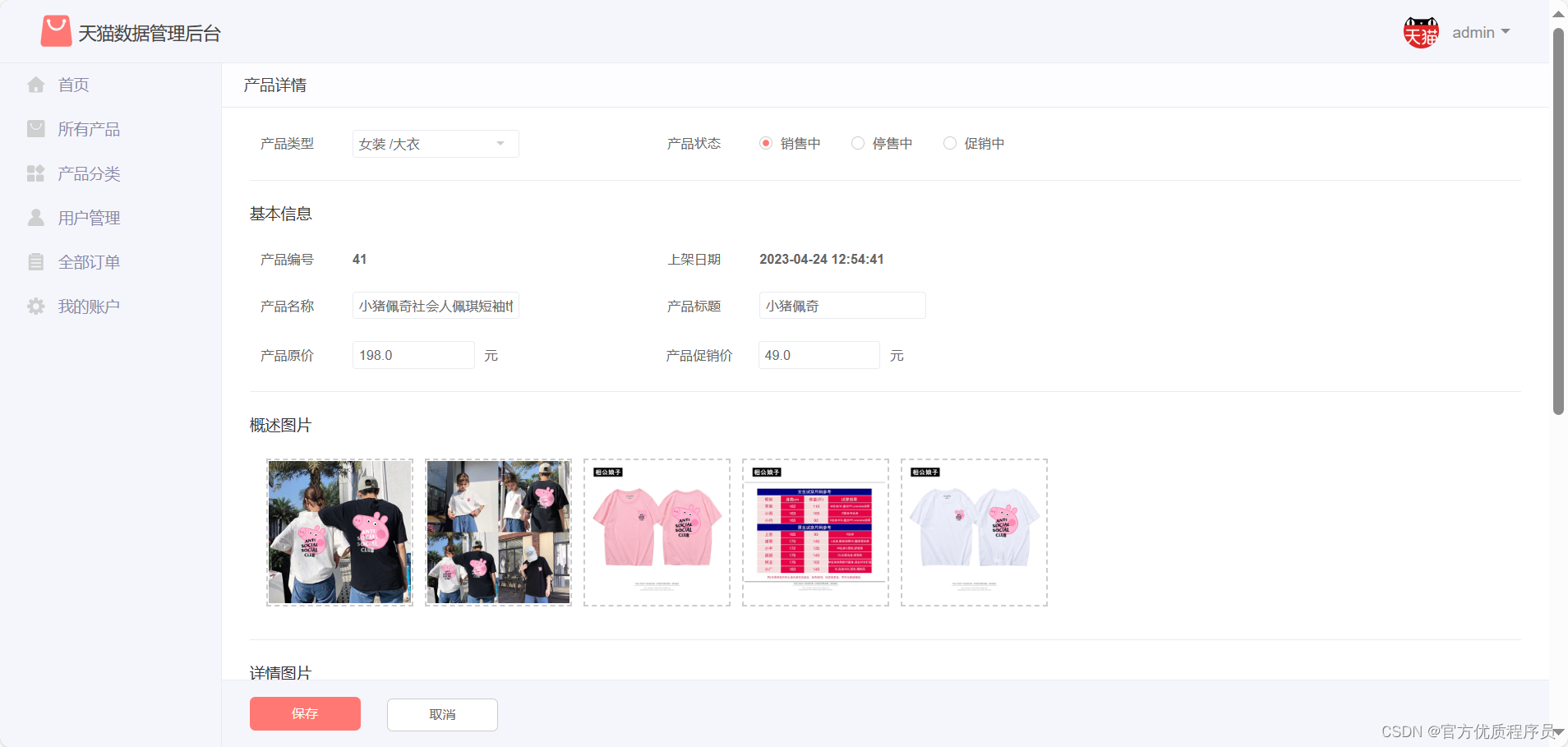
基于JAVA的天猫商场系统设计与实现,springboot+jsp,MySQL数据库,前台用户+后台管理,完美运行,有一万五千字论文
目录 演示视频 基本介绍 论文目录 系统截图 演示视频 基本介绍 基于JAVA的天猫商场系统设计与实现,springbootjsp,MySQL数据库,前台用户后台管理,完美运行,有一万五千字论文。 本系统在HTML和CSS的基础上…...
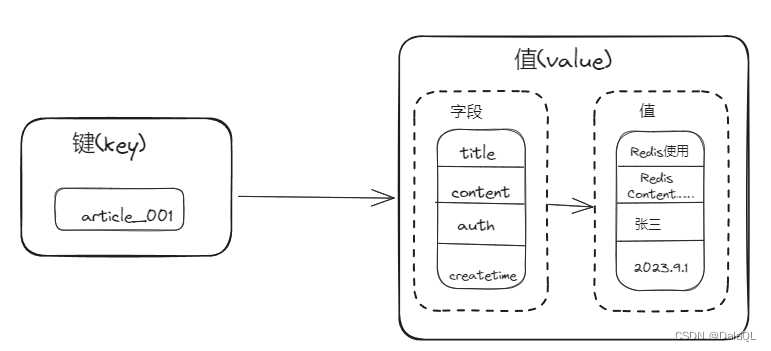
Redis学习
缓存定义 缓存是一个告诉数据交换的存储器,使用它可以快速的访问和操作数据。 常见缓存使用 本地缓存的常见使用:Spring Cache、MyBatis的缓存等 我的session存储和redis都放到缓存里面的,所有程序不管部署多少份,访问的都是r…...
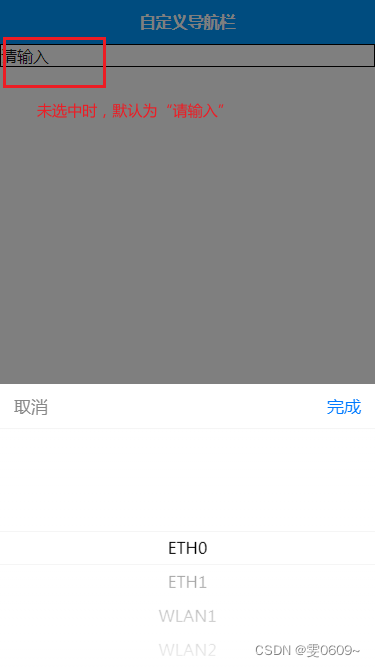
uni-app:实现picker下拉列表的默认值设置
效果 分析 1、在data中将index8的初始值设置为-1,表示未选择任何选项: index8: -1, //选择的下拉列表下标 2、在bindPickerChange8事件处理函数中添加条件判断。如果选择的值是-1,则将this.index8设置为"请输入",否则将…...
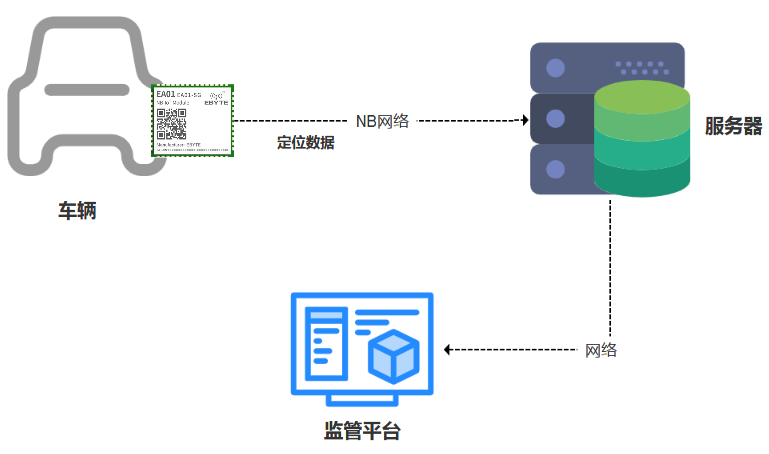
基于NB-iot技术实现财物跟踪的EA01-SG定位模块方案
NB-iot无线数传模块可做财物防盗窃器,让你的财物可定位跟踪! 随着社会的发展,公共资源及共享资源的蓬勃发展,对资产管理和资产追踪有了新的需求,如:某儿童玩具车在商场外面提供车辆乘坐游玩服务࿰…...

挑战吧,HarmonyOS应用开发工程师
一年一度属于工程师的专属节日1024,多重活动亮相啦~ 参与活动即有机会获得HUAWEI Freebuds 5i 耳机等精美礼品! 点击“阅读原文”查看更多活动详情!...
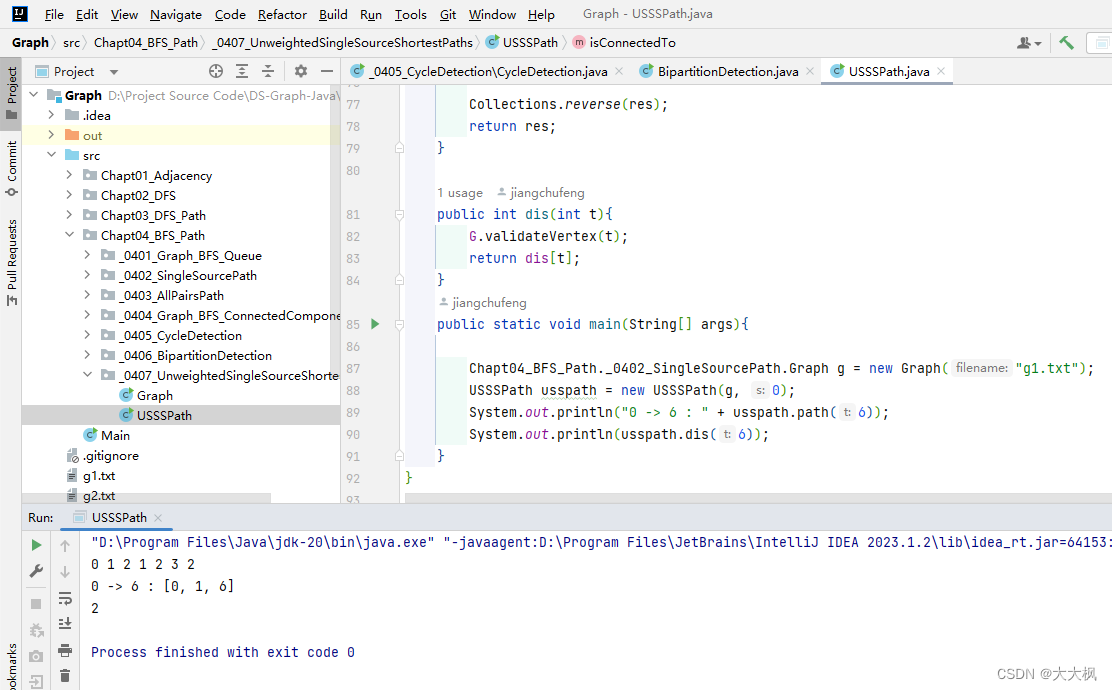
图论05-【无权无向】-图的广度优先BFS遍历-路径问题/检测环/二分图/最短路径问题
文章目录 1. 代码仓库2. 单源路径2.1 思路2.2 主要代码 3. 所有点对路径3.1 思路3.2 主要代码 4. 联通分量5. 环检测5.1 思路5.2 主要代码 6. 二分图检测6.1 思路6.2 主要代码6.2.1 遍历每个联通分量6.2.2 判断相邻两点的颜色是否一致 7. 最短路径问题7.1 思路7.2 代码 1. 代码…...
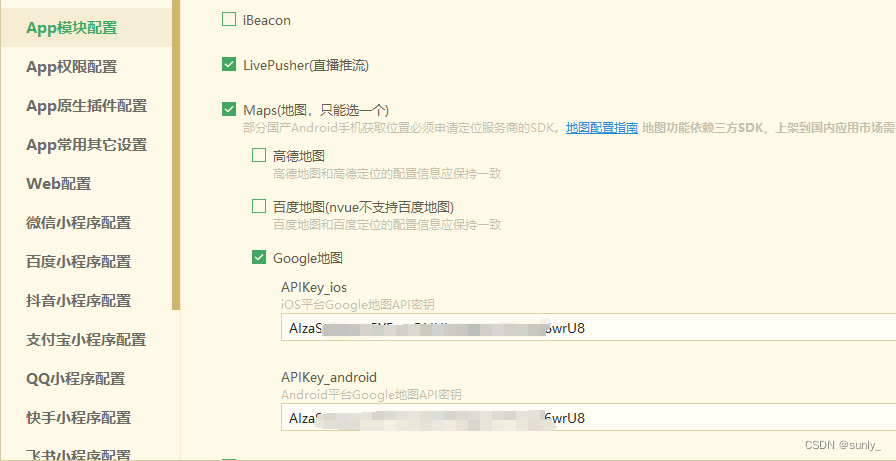
uniapp:谷歌地图,实现地图展示,搜索功能,H5导航
页面展示 APP H5 谷歌地图功能记录,谷歌key申请相对复杂一些,主要需要一些国外的身份信息。 1、申请谷歌key 以下是申请谷歌地图 API 密钥的流程教程: 登录谷歌开发者控制台:打开浏览器,访问 Google Cloud Platform Console。 1、创建或选择项目:如果你还没有创建项目…...
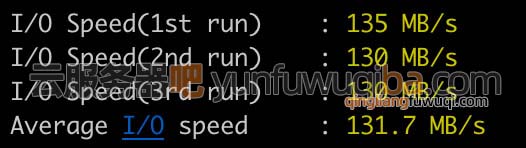
关于腾讯云轻量应用服务器性能测评,看这一篇文章就够了
腾讯云轻量应用服务器性能如何?为什么便宜是不是性能不行?腾讯云百科txybk.com从轻量应用服务器的CPU型号、处理器主频、内存、公网带宽、月流量和系统盘多方面来详细测评轻量性能,轻量应用服务器性价比高,并不是性能不行…...

HDFS集群NameNode高可用改造
文章目录 背景高可用改造方案实施环境准备配置文件修改应用配置集群状态验证高可用验证 背景 假定目前有3台zookeeper服务器,分别为zk-01/02/03,DataNode服务器若干; 目前HDFS集群的Namenode没有高可用配置,Namenode和Secondary…...
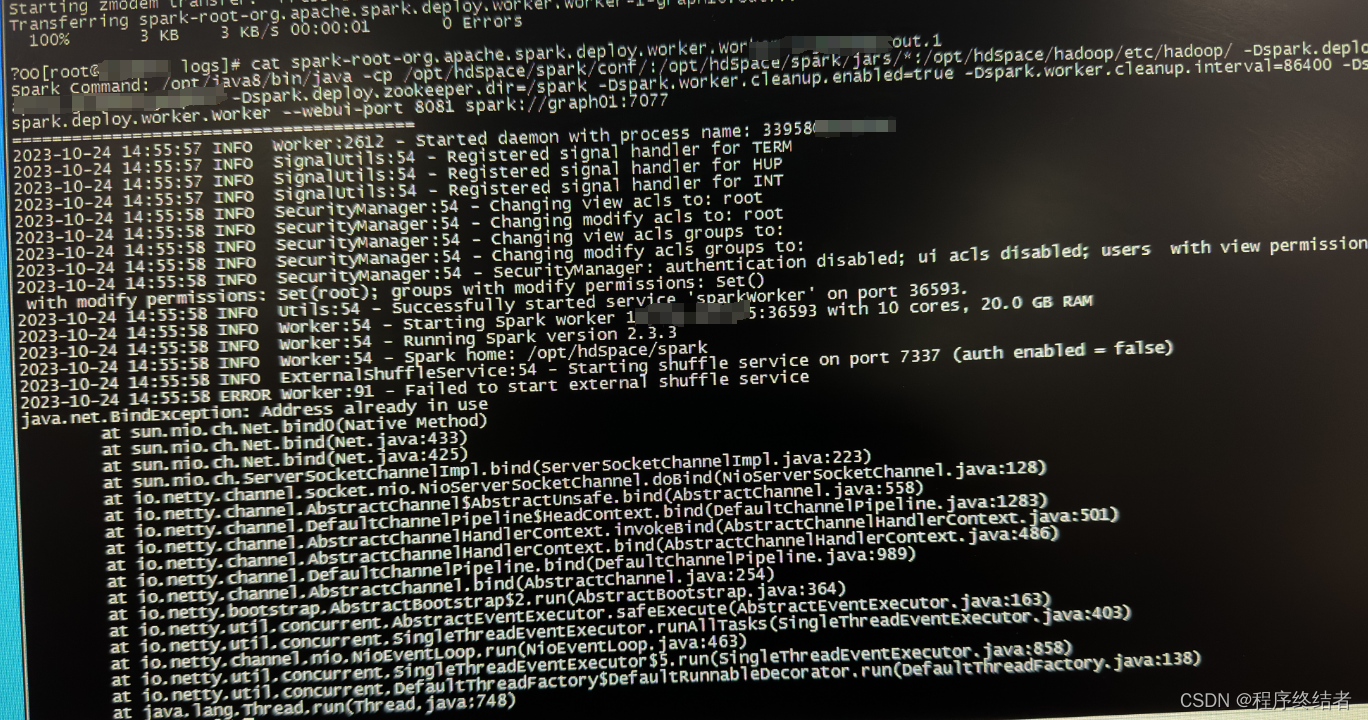
Spark集群中一个Worker启动失败的排错记录
文章目录 1 检查失败节点worker启动日志2 检查正常节点worker启动日志3 查看正常节点spark环境配置4 又出现新的ERROR4.1 报错解释4.2 报错解决思路4.3 端口报错解决操作 集群下电停机后再次启动时,发现其中一台节点的worker启动失败。 1 检查失败节点worker启动日…...

Mysql的JDBC知识点
什么是JDBC JDBC(Java DataBase Connectivity) 称为Java数据库连接,它是一种用于数据库访问的应用程序API,由一组用Java语言编写的类和接口组成,有了JDBC就可以用统一的语法对多种关系数据库进行访问,而不用担心其数据库操作语…...
git的实际操作
文章目录 删除GitHub上的某个文件夹克隆仓库到另一个仓库 删除GitHub上的某个文件夹 克隆仓库到另一个仓库 从原地址克隆一份裸板仓库 –bare创建的克隆版本库都不包含工作区,直接就是版本库的内容,这样的版本库称为裸版本库 git clone --bare ****(原…...

数据结构零基础C语言版 严蔚敏-线性表、顺序表
二、顺序表和链表 1. 线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串...... 线性表在逻辑上是线性结构,…...
Keil uVision 5 MDK版软件安装包下载及安装教程(最详细图文教程)
目录 一.简介 二.安装步骤 软件:Keil uvision5版本:MDKv518语言:中文/英文大小:377.01M安装环境:Win11/Win10/Win8/Win7硬件要求:CPU2.59GHz 内存4G(或更高)下载通道①百度网盘丨64位下载链接…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
