LeetCode 面试题 16.03. 交点
文章目录
- 一、题目
- 二、C# 题解
一、题目
给定两条线段(表示为起点 start = {X1, Y1} 和终点 end = {X2, Y2}),如果它们有交点,请计算其交点,没有交点则返回空值。
要求浮点型误差不超过 10^-6。若有多个交点(线段重叠)则返回 X 值最小的点,X 坐标相同则返回 Y 值最小的点。
示例 1:
输入:
line1 = {0, 0}, {1, 0}
line2 = {1, 1}, {0, -1}
输出: {0.5, 0}
示例 2:
输入:
line1 = {0, 0}, {3, 3}
line2 = {1, 1}, {2, 2}
输出: {1, 1}
示例 3:
输入:
line1 = {0, 0}, {1, 1}
line2 = {1, 0}, {2, 1}
输出: {},两条线段没有交点
提示:
- 坐标绝对值不会超过 2^7
- 输入的坐标均是有效的二维坐标
点击此处跳转题目。
二、C# 题解
这题写的心累,参考了 LeetCode 官方解法,代码如下:
public class Solution {public double[] Intersection(int[] start1, int[] end1, int[] start2, int[] end2) {int xa = start1[0], xb = end1[0], xc = start2[0], xd = end2[0];int ya = start1[1], yb = end1[1], yc = start2[1], yd = end2[1];double[] ans = { };if ((xa - xb) * (yc - yd) != (ya - yb) * (xc - xd)) { // 不平行int r = (xd - xc) * (yb - ya) - (yd - yc) * (xb - xa);int p = (xc - xa) * (yd - yc) - (yc - ya) * (xd - xc);int q = (xa - xc) * (yb - ya) - (ya - yc) * (xb - xa);double m = p * -1.0 / r, n = q * 1.0 / r;if (0 <= m && m <= 1 && 0 <= n && n <= 1) ans = new[] { xa + (xb - xa) * m, ya + (yb - ya) * m };}else if ((xa - xb) * (yc - ya) == (ya - yb) * (xc - xa)) { // 平行且在一条直线上Operation(xa, ya, xc, yc, xd, yd, ref ans);Operation(xb, yb, xc, yc, xd, yd, ref ans);Operation(xc, yc, xa, ya, xb, yb, ref ans);Operation(xd, yd, xa, ya, xb, yb, ref ans);}return ans;}private void Operation(int xp, int yp, int xa, int ya, int xb, int yb, ref double[] ans) {if (xp == xa && InLine(yp, ya, yb)) Update(xp, yp, ref ans);else if (xp != xa && InLine(xp, xa, xb)) Update(xp, yp, ref ans);}private bool InLine(int p, int a, int b) {return a <= p && p <= b || b <= p && p <= a;}private void Update(int x, int y, ref double[] ans) {if (ans.Length == 0) ans = new double[] { x, y };else if (Math.Abs(x - ans[0]) < 1e-6) ans[1] = y < ans[1] ? y : ans[1];else if (x < ans[0]) {ans[0] = x;ans[1] = y;}}
}
- 时间:124 ms,击败 66.67% 使用 C# 的用户
- 内存:41.04 MB,击败 100.00% 使用 C# 的用户
相关文章:

LeetCode 面试题 16.03. 交点
文章目录 一、题目二、C# 题解 一、题目 给定两条线段(表示为起点 start {X1, Y1} 和终点 end {X2, Y2}),如果它们有交点,请计算其交点,没有交点则返回空值。 要求浮点型误差不超过 10^-6。若有多个交点(…...

【码银送书第九期】《ChatGPT 驱动软件开发:AI 在软件研发全流程中的革新与实践》
计算机技术的发展和互联网的普及,使信息处理和传输变得更加高效,极大地改变了金融、商业、教育、娱乐等领域的运作方式。数据分析、人工智能和云计算等新兴技术,也在不断地影响和改变着各个行业。 如今,我们正在见证人工智能技术的…...
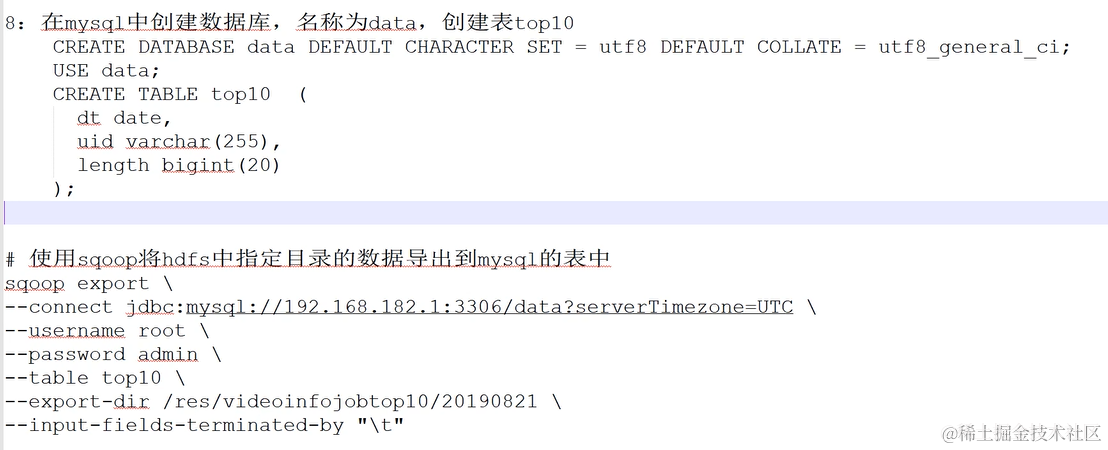
Hadoop3.0大数据处理学习4(案例:数据清洗、数据指标统计、任务脚本封装、Sqoop导出Mysql)
案例需求分析 直播公司每日都会产生海量的直播数据,为了更好地服务主播与用户,提高直播质量与用户粘性,往往会对大量的数据进行分析与统计,从中挖掘商业价值,我们将通过一个实战案例,来使用Hadoop技术来实…...

华为机试题:HJ3 明明的随机数
目录 第一章、算法题1.1)题目描述1.2)解题思路与答案1.3)牛客链接 友情提醒: 先看文章目录,大致了解文章知识点结构,点击文章目录可直接跳转到文章指定位置。 第一章、算法题 1.1)题目描述 题目描述&…...

Python OpenCV将n×n的小图拼接成m×m的大图
Python OpenCV将nn的小图拼接成mm的大图 前言前提条件相关介绍实验环境n \times n的小图拼接成m \times m的大图代码实现 前言 由于本人水平有限,难免出现错漏,敬请批评改正。更多精彩内容,可点击进入Python日常小操作专栏、OpenCV-Python小…...
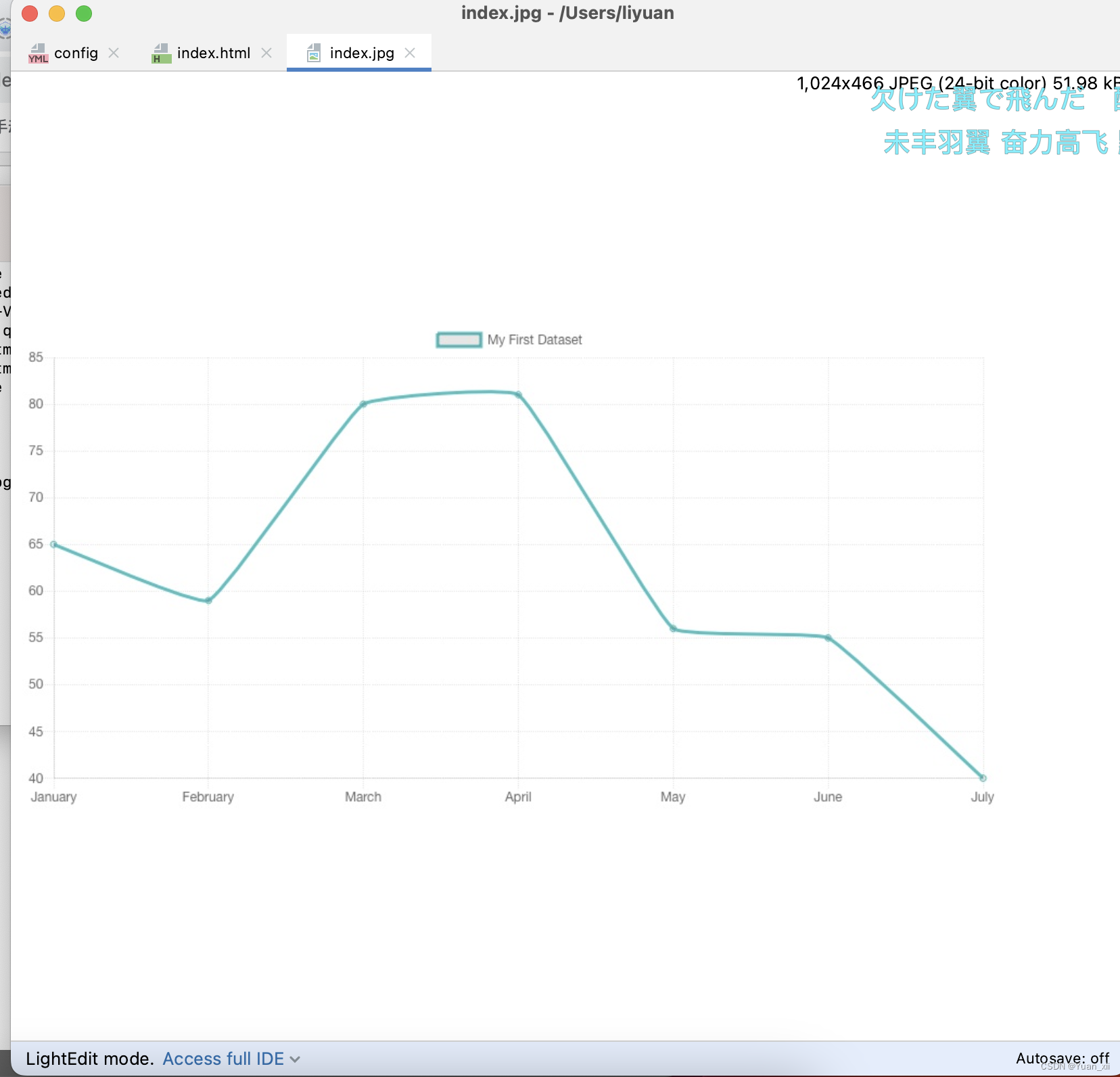
wkhtmltoimage/wkhtmltopdf 使用实践
1. 介绍 wkhtmltopdf/wkhtmltoimage 用于将简单的html页面转换为pdf或图片; 2.安装 downloads 2.1. mac os 下载64-bit 版本然后按照指示安装, 遇到 untrust developers 时,需要在 Settings -> Privacy 处信任下该安装包。 2.2. debian # 可用…...
Rclone连接Onedrive
一、Rclone介绍 Rclone是一款的命令行工具,支持在不同对象存储、网盘间同步、上传、下载数据。 我们这里连接的onedrive,其他网盘请查看官方文档。 注意: 需要先在Windows下配置好了,然后再将rclone配置文件复制到Linux的rclone配…...
RK356X/RK3588构建Ubuntu20.04根文件系统
文章目录 前言一、官网下载ubuntu-base二、挂载并构建文件系统2.1、配置构建文件系统环境2.2、编写挂载脚本mount.sh并安装相关工具2.3、轻量级的桌面环境 lubuntu-desktop2.4、卸载一些不必要的软件2.5、添加用户2.6 、允许root用户登录桌面2.7、串口自动登录2.8、添加分区释放…...

本地新建项目如何推到码云上去
1.先在码云上建立一个空仓库,正常步骤就行。建立完成有readme.md. 2.然后本地建立项目文件,正常脚手架搭建VUE\REACT等。记得要项目git init一下。 3.本地改好的内容commit 一下。 4.本地文件与远端仓库建立连接。git remote add origin https://gite…...
加密解密)
RSAUtil 前端 JavaScript JSEncrypt 实现 RSA (长文本)加密解密
文章归档:https://www.yuque.com/u27599042/coding_star/cl4dl599pdmtllw1 依赖 import JSEncrypt from ‘jsencrypt’ pnpm i jsencryptimport {stringIsNull} from “/utils/string_utils.js”:https://www.yuque.com/u27599042/coding_star/slncupw…...
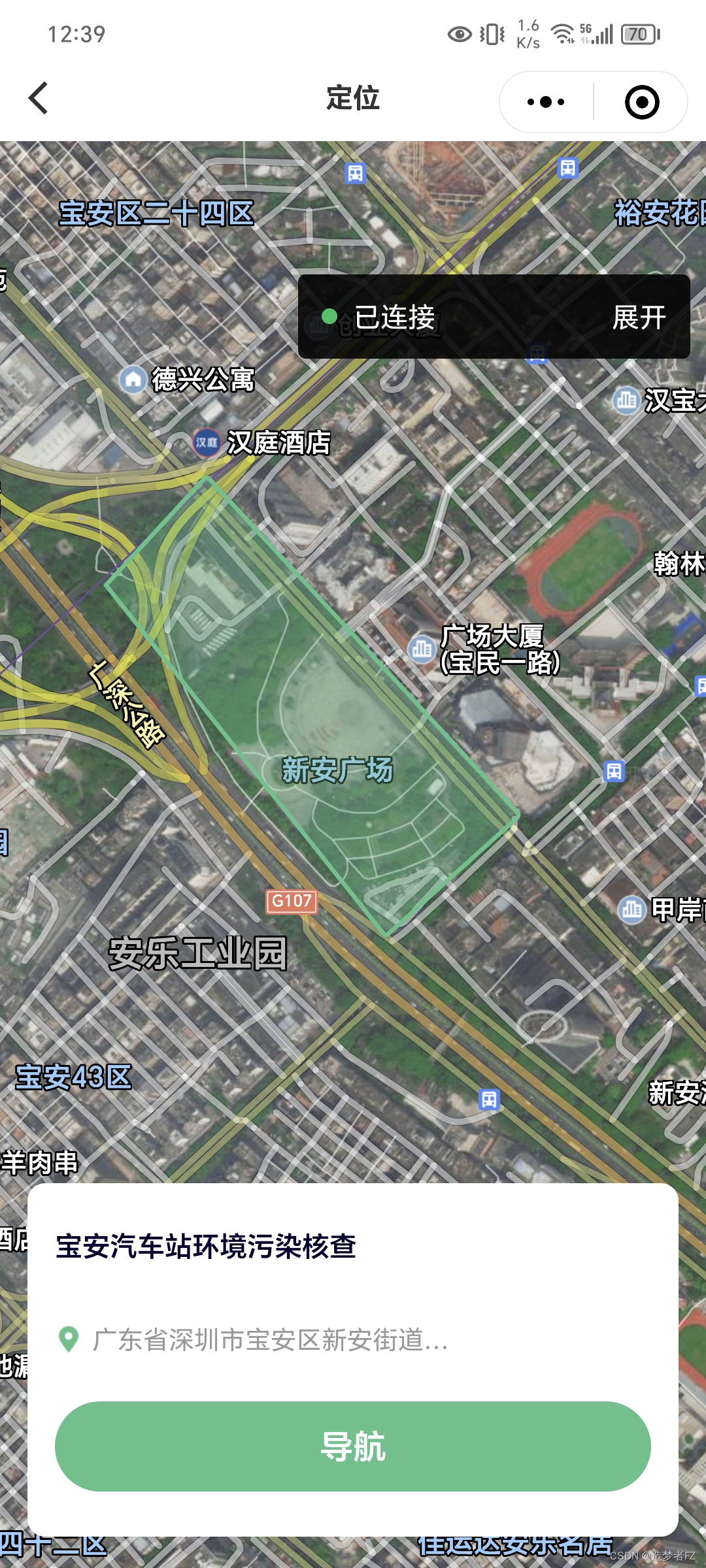
uniapp map polygons 区域填充色(fillColor)在ios显示正常,但在安卓手机显示是黑色的,怎么解决?
uniapp map polygons 区域填充色(fillColor)在ios显示正常,但在安卓手机显示是黑色的,怎么解决? <MapPage :longitude"item.centerCoord[0]" :latitude"item.centerCoord[1]":polygons"[{ points: it…...

OSCAR数据库上锁问题如何排查
关键字 oscar lock 问题描述 oscar 数据库上锁问题如何排查 解决问题思路 准备数据 create table lock_test(name varchar(10),age varchar(10));insert into lock_test values(ff,10); insert into lock_test values(yy,20); insert into lock_test values(ll,30);sessio…...

FPGA与人工智能泛谈-01
文章目录 前言一、FPGA(Field Programmable Gate Array)是什么?二、与GPU的对比1.GPU特点2. FPGA的优势三、人工智能实现的基础架构总结前言 人工智能技术的快速发展正从各个方面改变人类的生活、工作及教育等各个方面,其中人工智能算法的演进又是其中的关键一步,其中会涉及…...
【VASP】POTCAR文件
【VASP】POTCAR文件 POTCAR 文件的介绍qvasp 生成POTCARvaspkit 生成POTCAR再来认识一下各种赝势如何区分US、PAW、LDA、GGA、PW91 前言 一、4个常用的输入文件INCAR、POSCAR、POTCAR、KPOINTS INCAR: 计算任务类型是什么?怎么计算? KPOINTS: 包含了倒易…...

棒球俱乐部青少年成长体系·棒球1号位
棒球俱乐部青少年成长体系介绍 1. 培养理念 简要介绍棒球俱乐部的宗旨和培养青少年的目标 棒球俱乐部是一个致力于培养青少年棒球运动员的体育组织,其宗旨是通过提供专业的棒球训练和比赛机会,帮助青少年提高身体素质、培养团队合作精神和塑造积极向上…...
折叠式菜单怎么做编程,初学编程系统化教程初级1上线
中文编程系统化教程,不需英语基础,学习链接——入门篇课程 https://edu.csdn.net/course/detail/39036中文编程系统化教程,不需英语基础,学习链接—— 初级1课程 https://edu.csdn.net/course/detail/39061 ——————————…...

与AI对话,如何写好prompt?
玩转AIGC,优质的Prompt提示词实在是太重要了!同样的问题,换一个问法,就会得到差别迥异的答案。你是怎样和AI进行对话交流的呢?我来分享几个: 请告诉我…我想知道…对于…你有什么看法?帮我解决…...
基于YOLOv8模型和UA-DETRAC数据集的车辆目标检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOv8模型和UA-DETRAC数据集的车辆目标检测系统可用于日常生活中检测与定位汽车(car)、公共汽车(bus)、面包车(vans)等目标,利用深度学习算法可实现图片、视频、摄像头等方…...
)
0037【Edabit ★☆☆☆☆☆】【修改Bug 2】Buggy Code (Part 2)
0037【Edabit ★☆☆☆☆☆】【修改Bug 2】Buggy Code (Part 2) bugs language_fundamentals Instructions Fix the code in the code tab to pass this challenge (only syntax errors). Look at the examples below to get an idea of what the function should do. Exampl…...

【算法中的Java】— 判断语句
📒博客首页:Sonesang的博客 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 ❤️ :热爱Java与算法学习,期待一起交流! 🙏作者水平很有限,如果发现错误…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
