C++基础算法⑦——信奥一本通递归算法(放苹果、求最大公约数问题、2的幂次方表示、分数求和、因子分解、判断元素是否存在)
递归算法
- 1206:放苹果
- 1207:求最大公约数问题
- 1208:2的幂次方表示
- 1209:分数求和
- 1210:因子分解
- 1211:判断元素是否存在
1206:放苹果
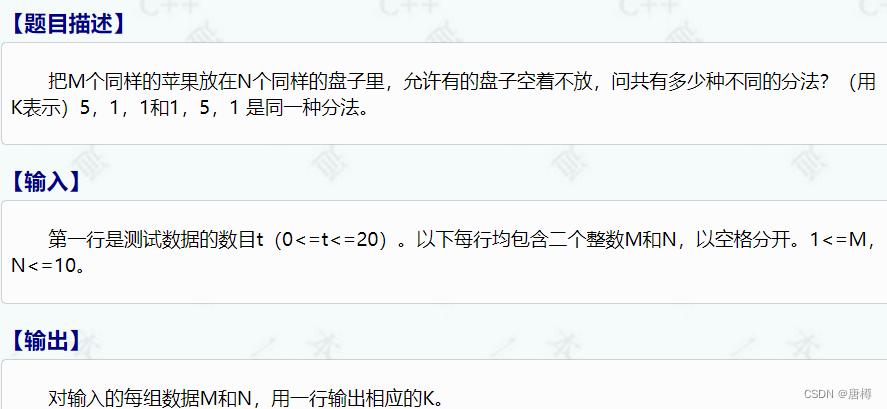
这道题还是有些难度的,我们要考虑几种放苹果的情况。我默默把m代表苹果,n代表盘子。
- 先把输入搞定,这个还是简简单单的。
int main(){//多苹果,少盘子 // 例如f(4)(3) = f(4-3)(3) + f(4)(2); // f(4)(2) = f(4-2)(2)+f(4)(1);//测试数据次数 cin>>t;for(int i=1;i<=t;i++){int a,b;cin>>a>>b; //输入每组数据 cout<<apple(a,b)<<endl; }return 0;
}
- 用apple函数求放苹果的次数。我们知道
多个苹果,0盘子; 多个苹果,1盘子;
0个苹果,多盘子;1个苹果,多盘子;
都只有一种方法哈。
if(m==0||m==1||n==0||n==1) return f[m][n]=1;
-
第二种放苹果情况,就是 少苹果 多盘子,应该怎么放?
注意 题目讲道:
1 2 第一个盘子放1个苹果,第二个盘子放2个苹果;
2 1 第一个盘子放2个苹果,第二个盘子放1个苹果;
是一样的,只算一种方法。
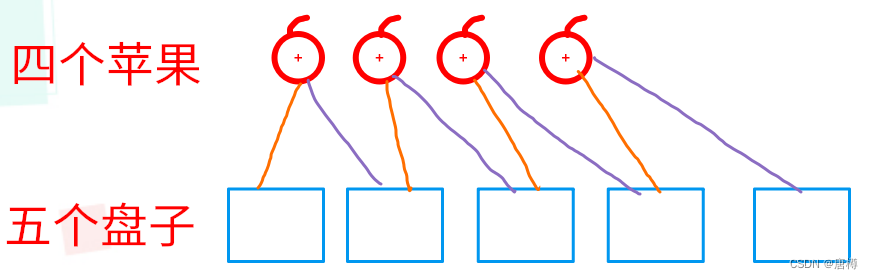
那上面图片:橙色线的放法 1 1 1 1 0 ;紫色线的放法 0 1 1 1 1 都算同一种; 4苹果🍎5盘子,其实就相当于 4苹果🍎4盘子的方法。代码表示则
return f[m][n] = apple(m,m);
- 最后一种情况:多苹果少盘子。
那这样,会出现每个盘子都至少有苹果🍎; 另外情况就是 有盘子没放苹果🍎; 把这两种可能加起来就是多苹果🍎少盘子的放法。
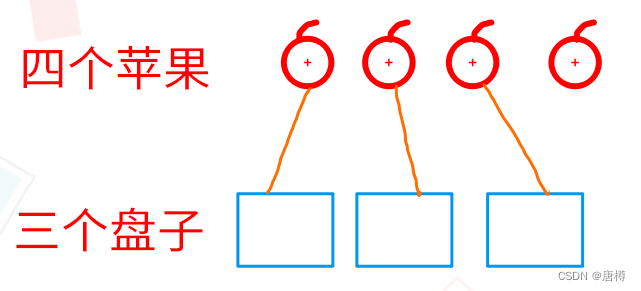
会出现每个盘子都至少有苹果🍎 那上面图片是不是有一个苹果没放对吧! 1个苹果3个盘子的放法是:
apple(4-3,3); //m苹果🍎,n盘子
apple(m-n,n);
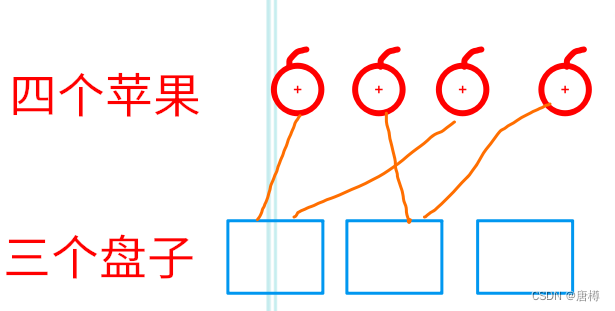
上图是有盘子没放苹果🍎的情况,则变成4个苹果🍎2个盘子的放法是:
apple(4,3-1); //m苹果🍎,n盘子
apple(m,n-1);
完整代码:
#include<bits/stdc++.h>
using namespace std;
int m,n,t; //m代表苹果,n代表盘子
int f[15][15]={0};
int apple(int m,int n){
// 多个苹果,0盘子; 多个苹果,1盘子;
// 0个苹果,多盘子;1个苹果,多盘子; 都只有一种 if(m==0||m==1||n==0||n==1) return f[m][n]=1;if(m>=n){ //多苹果,少盘子 return f[m][n] = apple(m-n,n) + apple(m,n-1);}else{return f[m][n] = apple(m,m);}}
int main(){//多苹果,少盘子 // 例如f(4)(3) = f(4-3)(3) + f(4)(2); // f(4)(2) = f(4-2)(2)+f(4)(1);//测试数据次数 cin>>t;for(int i=1;i<=t;i++){int a,b;cin>>a>>b; //输入每组数据 cout<<apple(a,b)<<endl; }return 0;
}1207:求最大公约数问题
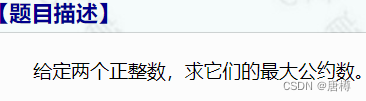
最大公约数用辗转相除法做即可。
#include<iostream>
using namespace std;
int gcd(int a,int b){if(b==0) return a;return gcd(b,a%b);
}int a,b;
int main(){cin>>a>>b;cout<<gcd(a,b);return 0;
}
1208:2的幂次方表示

- 输入一个值,这个值从0次方开始拆分
int main(){int n;cin>>n;f(n,0); return 0;
}
173 怎么得出2的几次方呢? 值n用短除法,不断➗2,有余数1代表次方有。除一次2,就次方k+1;直到n除到0结束。
void f(int n,int k){ //n是值,k是几方数 if(n==0) return ; //值0,结束 n /= 2;f(n,k+1); //不断除2,往下搜
根据题目要求,分解要在余数为1的情况:
- 2的0次方分解: 2(0)
- 2的1次方分解: 2
- 2的2次方分解: 2(2)
- 2的2次方以上分解: 以次方k的值作为n,重新调用函数进行次方的再次分解。
if(yu==1){ //有余数,就输出
// cout<<"2("<<k<<")";if(k==0) cout<<"2(0)";else if(k==1) cout<<"2";else if(k==2) cout<<"2(2)"; else{ //超过2的次方重新模拟调用 cout<<"2(";f(k,0);//对7再进行模拟cout<<")"; }}
题目输出要有+号。注意当有余数和值不为0情况。
if(n!=0 && yu!=0) cout<<"+";
完整代码:
#include<bits/stdc++.h>
using namespace std;
void f(int n,int k){ //k是次方数 if(n==0) return ; //值0,结束 int yu = n % 2; //求余数 n /= 2;f(n,k+1); //不断除2,往下搜
// 2进制数,哪个次方数是1、是0; 137= 010001001; 128+8+1if(n!=0 && yu!=0) cout<<"+"; if(yu==1){ //有余数,就输出
// cout<<"2("<<k<<")";if(k==0) cout<<"2(0)";else if(k==1) cout<<"2";else if(k==2) cout<<"2(2)"; else{ //超过2的次方重新模拟调用 cout<<"2(";f(k,0);//对7再进行模拟cout<<")"; }}
}
int main(){int n;cin>>n;f(n,0); return 0;
}
1209:分数求和
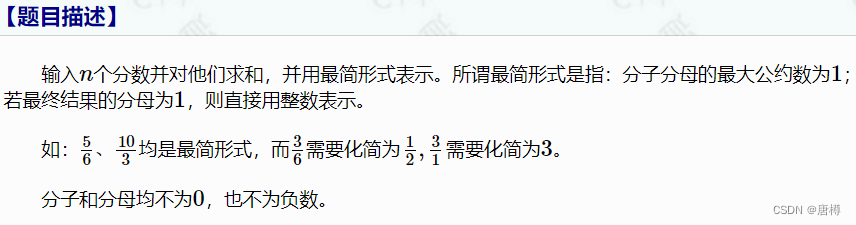

由题目可知,要模拟出分数相加的情况,也就是分母相乘,分子通分求和,在最后进行化简。
- 要定义变量,第一次输入值 表示第一个数的分子,分母。
int main(){int a,b,n,fz,fm;char c;cin>>n;cin>>a>>c>>b;fz = a;fm = b;
- 接着从第二个值的分数到第n个分数逐个输入,输入一个分数我们就进行通分操作。
for(int i=2;i<=n;i++){cin>>a>>c>>b;
- 分子通分:
fz = fz*b + fm*a; //分子 - 分母相乘:
fm = fm*b; //分母
- 对通分的结果,进行最简化,那我们要同时分子分母除以最大的共同因子,也就是最大公约数。
int gcd(int a,int b){if(b==0) return a;return gcd(b,a%b);
}int yue = gcd(fz,fm);fz /= yue; //约分 fm /= yue; //约分
最后判断分母是1就直接输出分子。
if(fm==1) cout<<fz<<endl; //分母是1,直接输出分子else cout<<fz<<"/"<<fm<<endl;
完整代码:
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b){if(b==0) return a;return gcd(b,a%b);
}
int main(){int a,b,n,fz,fm;char c;cin>>n;cin>>a>>c>>b;fz = a;fm = b;for(int i=2;i<=n;i++){cin>>a>>c>>b;fz = fz*b + fm*a; //分子 fm = fm*b; //分母int yue = gcd(fz,fm);fz /= yue; //约分 fm /= yue; //约分 }if(fm==1) cout<<fz<<endl; //分母是1,直接输出分子else cout<<fz<<"/"<<fm<<endl; return 0;
}1210:因子分解
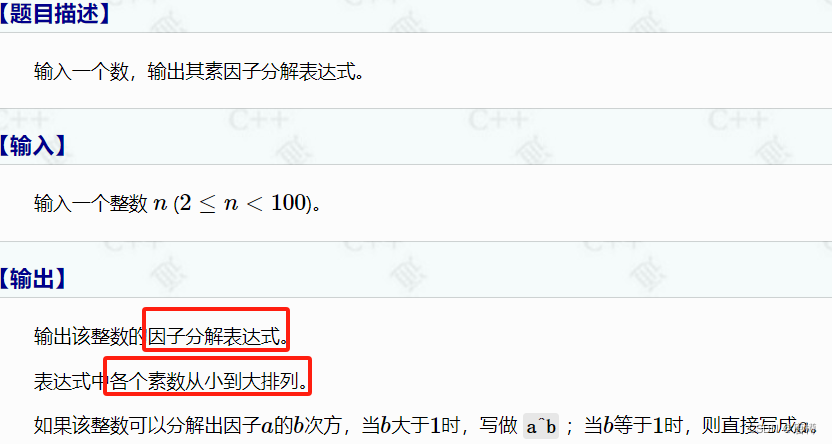
对n 从2到n进行除法,能被整除代表改因子可以分解。
int main(){int n,cnt=0,f=0;cin>>n;for(int i=2;i<=n;i++){//判断整除}
如果能被整除,就统计这个因子 i 的次数 cnt+1。接着再对n进行分解,直到分解不了。
// 1.判断能被整除if(n%i==0){cnt = 0; //统计分解的次数while(n%i==0){ //实现数字的分解 n = n/i;cnt++;}
再这个因子的次数有无超过1,有要输出 “^”;
乘号 * 输出在两个数中间。 最后判断n分解到值1就结束循环。
if(f==0) f=1; //保证乘号不能第一次else cout<<"*";cout<<i;if(cnt>1) cout<<"^"<<cnt;if(n==1) return 0;
完整代码
#include<bits/stdc++.h>
using namespace std;
int main(){int n,cnt=0,f=0;cin>>n;for(int i=2;i<=n;i++){
// 1.判断能被整除if(n%i==0){cnt = 0; //统计分解的次数while(n%i==0){ //实现数字的分解 n = n/i;cnt++;}if(f==0) f=1;else cout<<"*";cout<<i;if(cnt>1) cout<<"^"<<cnt;if(n==1) return 0; } } return 0;
}
1211:判断元素是否存在
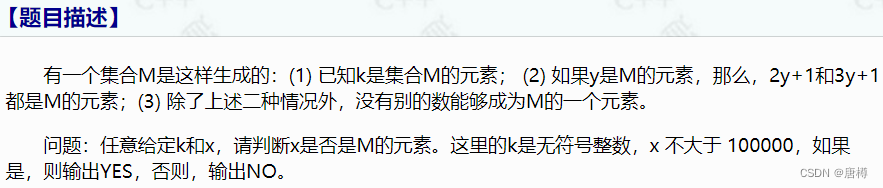

1.题目输入需要用到,c语言的输入方式。输入完判断是否满足条件,是就输出YES,否则NO。用函数去完成判断条件
int main(){
// cin>>k>>x;scanf("%d,%d",&k,&x);if(search(k)){cout<<"YES";}else{cout<<"NO";}return 0;
}
- x等于k也是满足函数条件,意味x是M的元素,因为k本身是M的元素
int x,k;
int search(int y){ //主函数k的值传到yif(y==x){return true;}
当x<k是 不会满足2k+1和3k+1 的条件。
if(y>x){return false;}
当x>k是 调用下函数是否满足2k+1和3k+1 的条件。
if(x>y){return search(2*y+1) || search(3*y+1);}
完整代码:
#include<bits/stdc++.h>
using namespace std;
int x,k;
int search(int y){if(y==x){return true;} if(y>x){return false;}if(x>y){return search(2*y+1) || search(3*y+1);}
}
int main(){
// cin>>k>>x;scanf("%d,%d",&k,&x);if(search(k)){cout<<"YES";}else{cout<<"NO";}return 0;
}
相关文章:

C++基础算法⑦——信奥一本通递归算法(放苹果、求最大公约数问题、2的幂次方表示、分数求和、因子分解、判断元素是否存在)
递归算法 1206:放苹果1207:求最大公约数问题1208:2的幂次方表示1209:分数求和1210:因子分解1211:判断元素是否存在 1206:放苹果 这道题还是有些难度的,我们要考虑几种放苹果的情况。…...
uni-app医院智能导诊系统源码
随着科技的迅速发展,人工智能已经逐渐渗透到我们生活的各个领域。在医疗行业中,智能导诊系统成为了一个备受关注的应用。本文将详细介绍智能导诊系统的概念、技术原理以及在医疗领域中的应用,分析其优势和未来发展趋势。 智能导诊系统通过人工…...

启动jar时指定nacos配置
背景 由于需要在不同服务上部署应用,避免频繁打包,需要在jar启动时灵活配置naocs配置 启动命令 java -Xms256m -Xmx512m -Dfile.encodingutf-8 -jar mes-gateway-1.0.1.jar --spring.cloud.nacos.discovery.server-addrhttp://127.0.0.1:8848 --spri…...
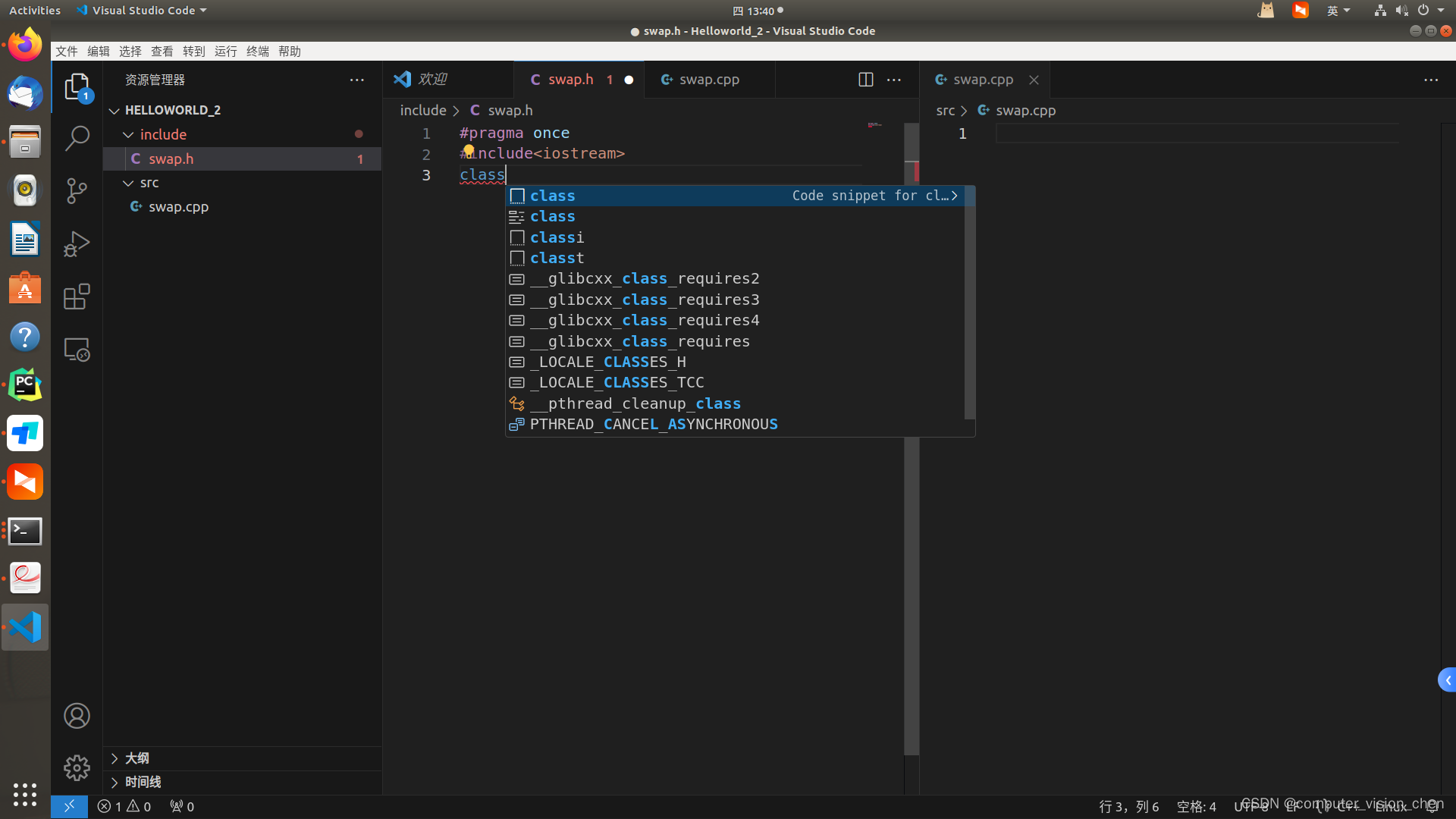
linux安装vscode vscode使用 创建项目并运行
下载 https://code.visualstudio.com/ 下载.deb文件 安装 假如文件被下载到了 /opt目录下 进入Opt目录,右键从当前目录打开终端。 输入下面的安装命令。 sudo apt-get install ./code_1.83.1-1696982868_amd64.deb 安装成功。 安装插件 使用c,必…...

如何解决数据倾斜
星光下的赶路人star的个人主页 臣书刷字墨淋漓,舒卷烟云势最奇 文章目录 1、数据倾斜的现象2、解决办法2.1 单表聚合(group bysum())2.2 多表关联(join) 3、倾斜原因 1、数据倾斜的现象 部分Reduce一直运行࿰…...
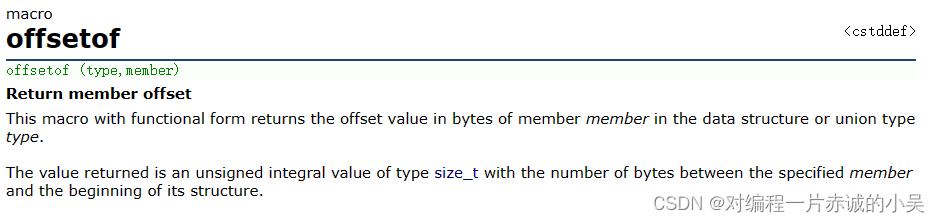
宏定义实现offsetof
在C语言中,有这样一个特殊的宏,叫offsetof,它的功能是啥呢? 我们来看看它的介绍 它的功能是:返回一个结构体的成员的大小(相较于起始地址的偏移量) 引用代码:http://t.csdnimg.cn…...

YOLOv5— Fruit Detection
🍨 本文为[🔗365天深度学习训练营学习记录博客 🍦 参考文章:365天深度学习训练营-第7周:咖啡豆识别(训练营内部成员可读) 🍖 原作者:[K同学啊 | 接辅导、项目定制](https…...

(PyTorch)PyTorch中的常见运算(*、@、Mul、Matmul)
1. 矩阵与标量 矩阵(张量)每一个元素与标量进行操作。 import torch a torch.tensor([1,2]) print(a1) >>> tensor([2, 3]) 2. 哈达玛积(Mul) 两个相同尺寸的张量相乘,然后对应元素的相乘就是这个哈达玛…...

cmd 命令关闭占用端口
工作中还是偶尔会遇到端口号被占用的情况,之前也有写过另一种关闭方式,但是发现没有命令方便,所以记录一下。 1、 查看 8081 端口占用的 pid 。 命令:netstat -ano |findstr 8081 由上图可知,占用 8081 端口的进程 id…...

PG14启动报错“max_stack_depth“ must not exceed 7680kB
问题描述 PG14编译安装后启动报错"max_stack_depth" must not exceed 7680kB [roottop132:/pgdb/data]$ systemctl start postgres Job for postgres.service failed because the control process exited with error code. See "systemctl status postgres.se…...

BES2700 蓝牙协议之RFCOMM通道使用方法
是否需要申请加入数字音频系统研究开发交流答疑群(课题组)?可加我微信hezkz17, 本群提供音频技术答疑服务 BES2700 RFCOMM通道使用方法 RFCOMM_CHANNEL_NUM 枚举定义了一系列的通道号码,并为每个通道号码指定了一个具体的名称。以下是其中一些通道的中文含义: RFCOMM_CHAN…...

简单介绍一下迁移学习
迁移学习是一种机器学习技术,旨在利用从一个任务或领域学习到的知识来改善另一个任务或领域的学习性能。在传统的机器学习方法中,通常假设训练数据和测试数据是从相同的分布中独立同分布采样的。然而,在现实世界中,这个假设并不总…...

PHP 同城服务共享茶室小程序系统是如何实现的?
随着互联网的快速发展和共享经济的兴起,同城服务共享茶室作为一种新型的商业模式,越来越受到人们的关注。通过开发一款基于PHP的同城服务共享茶室小程序系统,可以提供更加便捷、高效、个性化的服务体验。本文将详细介绍PHP同城服务共享茶室小…...

JavaScript对象与原型
目录 对象的创建 原型与原型链 原型继承 总结 在JavaScript中,对象是非常重要的概念之一。它们允许我们以一种结构化的方式存储和组织数据,并提供了一种方便的方式来操作和访问这些数据。而对象的行为和属性则通过原型来定义。 对象的创建 在JavaS…...

论文解读:《DataPype:用于计算机辅助药物设计的全自动统一软件平台》
论文解读:《DataPype: A Fully Automated Unified Software Platform for Computer-Aided Drug Design》 1.文章概述2.背景2.方法2.1 DataPype概述2.2 数据2.3 分子和蛋白质数据的处理2.3.1 配体处理2.3.2 蛋白质加工 2.4 CADD方法2.5 基准研究2.5.1 单个 CADD 制备…...

2023年Flutter教程_Flutter+Getx仿小米商城项目实战视频教程-V3版
Flutter是谷歌公司开发的一款开源、免费的UI框架,可以让我们快速的在Android和iOS上构建高质量App。它最大的特点就是跨平台、以及高性能。 目前 Flutter 已经支持 iOS、Android、Web、Windows、macOS、Linux 的跨平台开发。 GetX 是 Flutter 上的一个轻量且强大的解…...

【Spring Boot系列】- Spring Boot事务应用详解
【Spring Boot系列】- Spring Boot事务应用详解 一、事务简介 事务(Transaction)是数据库操作最基本单元,逻辑上一组操作,要么都成功。如果有一个操作失败。则事务操作都失败(回滚(Rollback)&…...
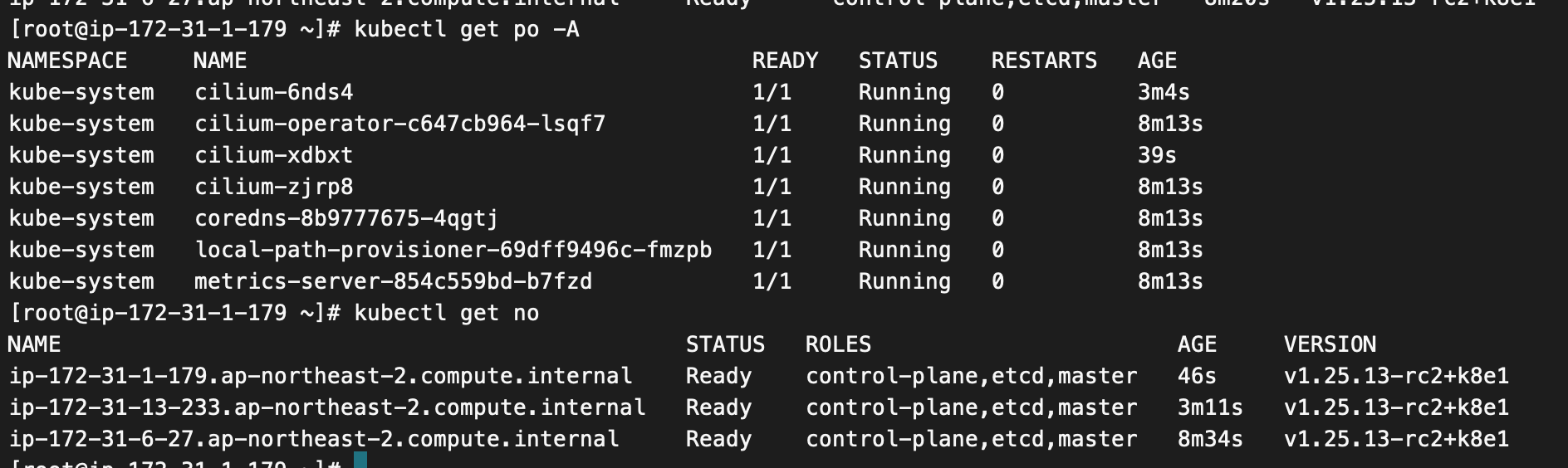
28. 使用 k8e 玩转 kube-vip with Cilium‘s Egress Gateway 特性
因为在私有云环境下,我们需要保障集群服务 APIServer地址的高可用,所以提供的方案就是使用一个 VIP 让 API Server 的流量可以负载均衡的流入集群。另外,kube-vip 还支持 Service LB,方便SVC 服务的负载均衡,结合 cilium Egress Gateway 特性可以做到集群内的容器对外访问…...

webrtc ios build signing
构建命令 $ gn gen out/ios --argstarget_os"ios" target_cpu"arm64" rtc_include_testsfalse --idexcode报错,这个错误是因为存在多个签名的问题,通过错误信息知道其中有一个是无效的(被吊销),移…...
【接口测试】Jmeter接口实战-Dubbo接口+造10W数据测试(详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Windows环境通…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
