【C++进阶之路】第三篇:二叉搜索树 kv模型
文章目录
- 一、二叉搜索树
- 1.二叉搜索树概念
- 2.二叉搜索树操作
- 3.二叉搜索树的实现
- 二、二叉搜索树的应用
- 1.kv模型
- 2.kv模型的实现
- 三、 二叉搜索树的性能分析
一、二叉搜索树
1.二叉搜索树概念
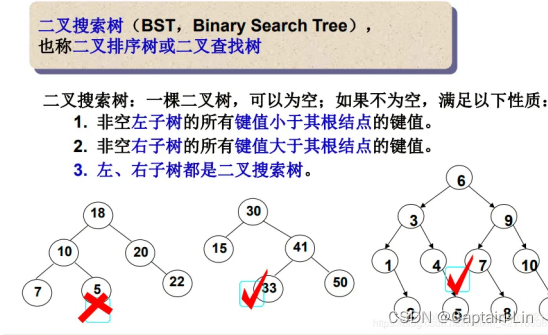
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
2.二叉搜索树操作
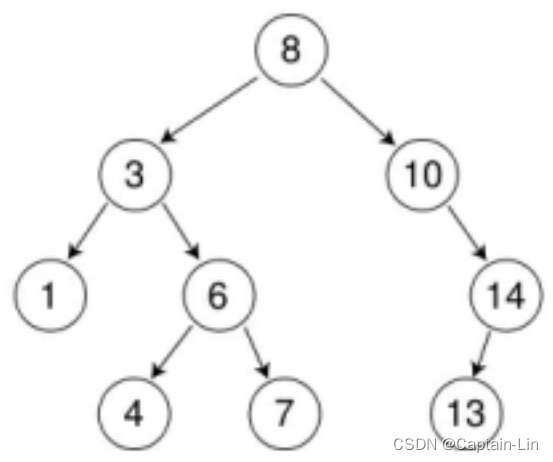
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
(1)二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到到空,还没找到,这个值不存在。
(2)二叉搜索树的插入
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
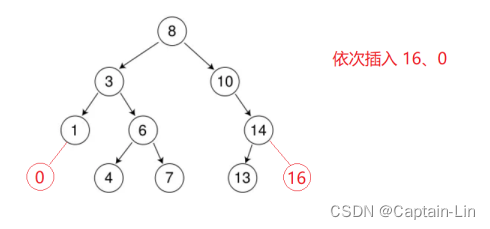
(3)二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回,否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
- 情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题–替换法删除
注意:
使用替换法删除,我们通常替换所需删除节点右树中的最小节点,即所需删除节点右树区域的最左节点。需要与被删除节点替换的节点可能左为空,所以我们不能直接删除它,我们还要多做一些工作–要考虑情况c发生的可能性,做情况c一样的工作。
使用替换法删除,还要考虑根节点的删除问题(根节点就是所需删除节点右树区域的最左节点)
3.二叉搜索树的实现
- BSTree.h
namespace key
{template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:/*BSTree():_root(nullptr){}*/BSTree() = default; // 制定强制生成默认构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);//_root = nullptr;}bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);// 链接if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 1、左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;} // 2、右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 找右树最小节点替代,也可以是左树最大节点替代Node* pminRight = cur;Node* minRight = cur->_right;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (pminRight->_left == minRight) //考虑根节点,做判断{pminRight->_left = minRight->_right; //正常节点}else{pminRight->_right = minRight->_right; //根节点}delete minRight;}return true;}}return false;}protected:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}private:Node* _root = nullptr;};
}
- Test.cpp
void TestBSTree1()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };key::BSTree<int> t1;for (auto e : a){t1.Insert(e);}//t1.InOrder(t1.GetRoot());t1.InOrder();/*t1.Erase(7);t1.InOrder();t1.Erase(14);t1.InOrder();t1.Erase(3);t1.InOrder();*/t1.Erase(8);t1.InOrder();for (auto e : a){t1.Erase(e);t1.InOrder();}t1.InOrder();
}int main()
{TestBSTree1();return 0;
}
二、二叉搜索树的应用
1.kv模型
-
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
-
以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
-
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误
-
-
KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
2.kv模型的实现
- 改造二叉搜索树为KV结构
// 改造二叉搜索树为KV结构
namespace key_value
{// BinarySearchTree -- BSTree// SearchBinaryTreetemplate<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);// 链接if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 1、左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;} // 2、右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 找右树最小节点替代,也可以是左树最大节点替代Node* pminRight = cur;Node* minRight = cur->_right;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else{pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}protected:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};
}
- 测试用例
// 测试用例
void TestBSTree2()
{key_value::BSTree<string, string> dict;dict.Insert("sort", "排序");dict.Insert("left", "左边");dict.Insert("right", "右边");dict.Insert("string", "字符串");dict.Insert("insert", "插入");dict.Insert("erase", "删除");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << ":" << ret->_value << endl;}else{cout << "无此单词" << endl;}}
}void TestBSTree3()
{string arr[] = { "西瓜", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉", "梨" };key_value::BSTree<string, int> countTree;for (auto str : arr){//key_value::BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == nullptr){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();
}int main()
{TestBSTree3();return 0;
}
三、 二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log_2 N(以2为底N的对数)
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N
结论:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?依据AVL树和红黑树的知识可以很好的解决,这两个知识小编会在后续章节讲解,此处先不做深入赘述。
相关文章:

【C++进阶之路】第三篇:二叉搜索树 kv模型
文章目录 一、二叉搜索树1.二叉搜索树概念2.二叉搜索树操作3.二叉搜索树的实现 二、二叉搜索树的应用1.kv模型2.kv模型的实现 三、 二叉搜索树的性能分析 一、二叉搜索树 1.二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性…...
【Oracle】Navicat Premium 连接 Oracle的两种方式
Navicat Premium 使用版本说明 Navicat Premium 版本 11.2.16 (64-bit) 一、配置OCI 1.1 配置OCI环境变量 1.1.2 设置\高级系统设置 1.1.2 系统属性\高级\环境变量(N) 1.1.3 修改/添加系统变量 ORACLE_HOME ORACLE_HOME D:\app\root\product\12.1.0\dbhome_11.1.4 添加系…...

在python里如何实现switch函数的功能
在许多编程语言中,包括Python,都提供了switch语句或类似的功能来根据不同的条件执行不同的代码块。然而,Python本身并没有内置的switch语句,但是您可以使用其他方式来实现类似的功能。下面是一种常见的方法: 使用if-e…...

Python 继承和子类示例:从 Person 到 Student 的演示
继承允许我们定义一个类,该类继承另一个类的所有方法和属性。父类是被继承的类,也叫做基类。子类是从另一个类继承的类,也叫做派生类。 创建一个父类 任何类都可以成为父类,因此语法与创建任何其他类相同: 示例&…...
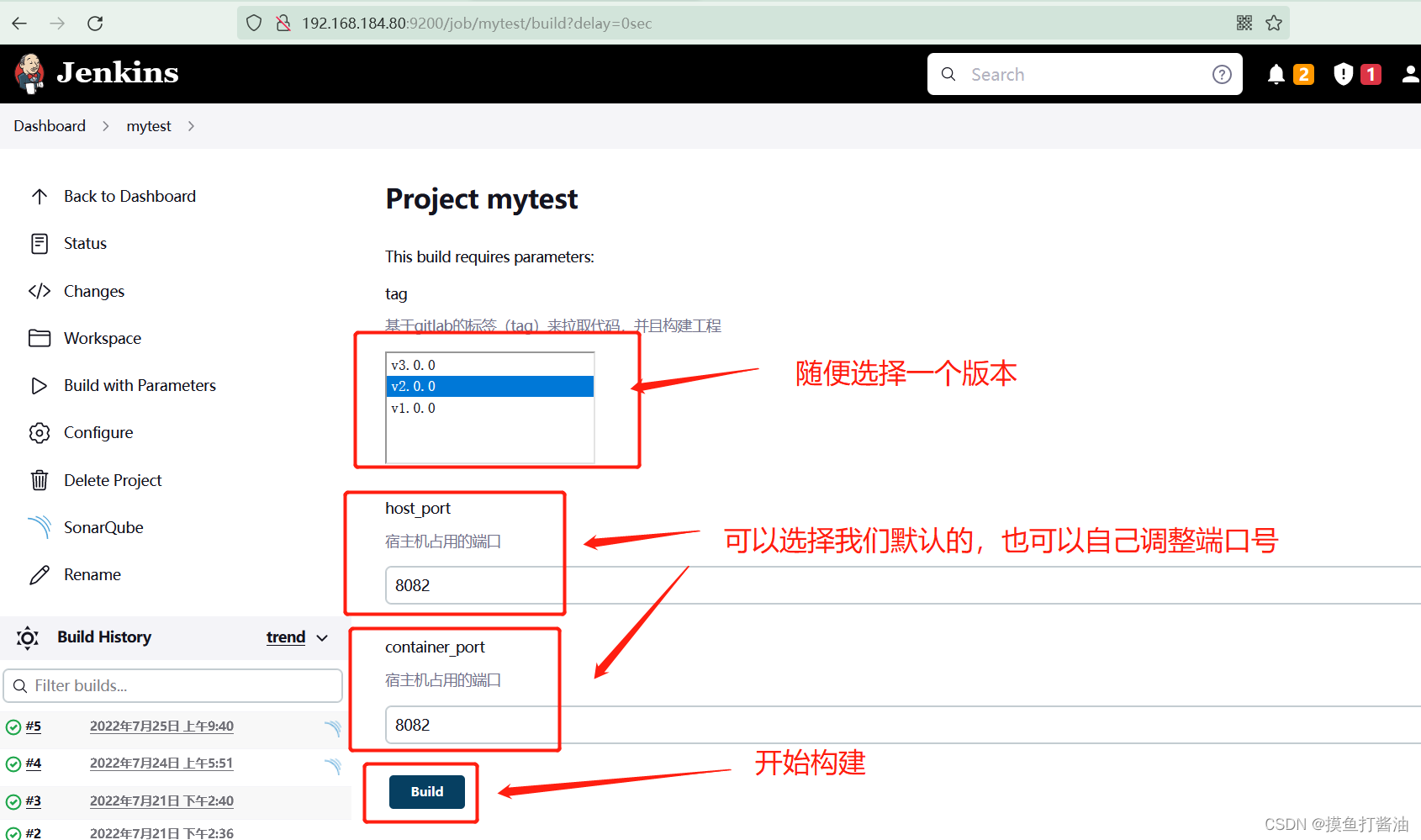
DevOps持续集成-Jenkins(3)
文章目录 DevOpsDevOps概述Jenkins实战3:实战1和实战2的加强版(新增SonarQube和Harbor)⭐环境准备⭐项目架构图对比Jenkins实战1和实战2,新增内容有哪些?SonarQube教程采用Docker安装SonarQube (在Jenkins所…...
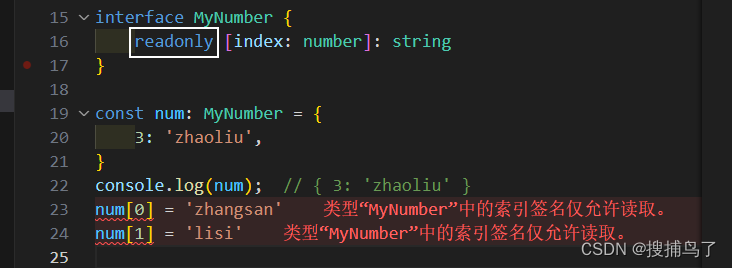
TypeScript之索引签名
1. 索引签名 在 TypeScript 中,索引签名是一种定义对象类型的方式,它允许我们使用字符串或数字作为索引来访问对象的属性。 索引签名最主要的作用就是允许我们动态地添加或访问对象的属性,通过使用索引签名,我们可以在编译时无法…...
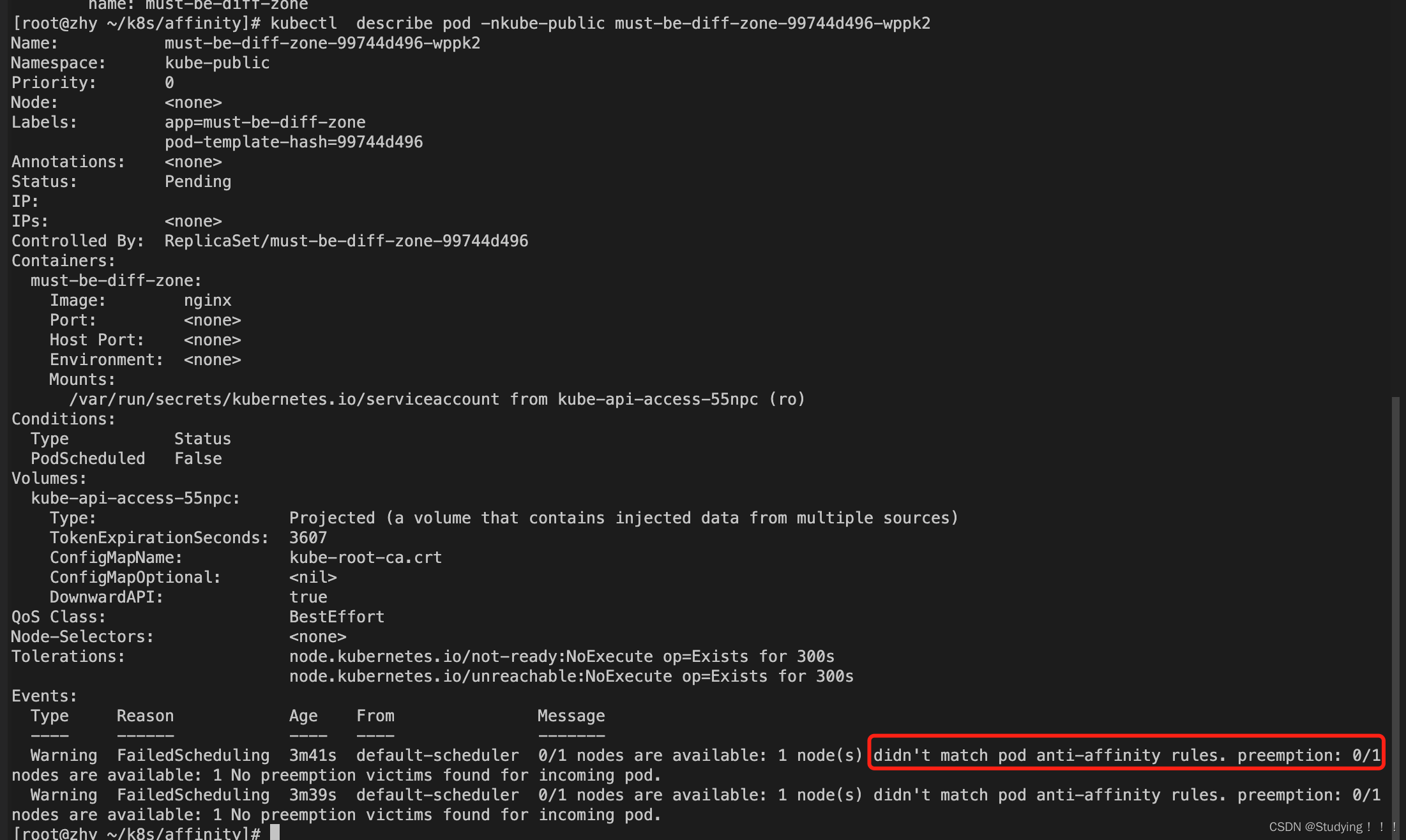
k8s-----24、亲和力Affinity
1、应用场景 pod和节点间的关系: 某些Pod优先选择有ssdtrue标签的节点,如果没有在考虑部署到其它节点;某些Pod需要部署在ssdtrue和typephysical的节点上,但是优先部署在ssdtrue的节点上; pod和pod间的关系: 同一个应用的Pod不…...

860. 柠檬水找零
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。 每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,…...
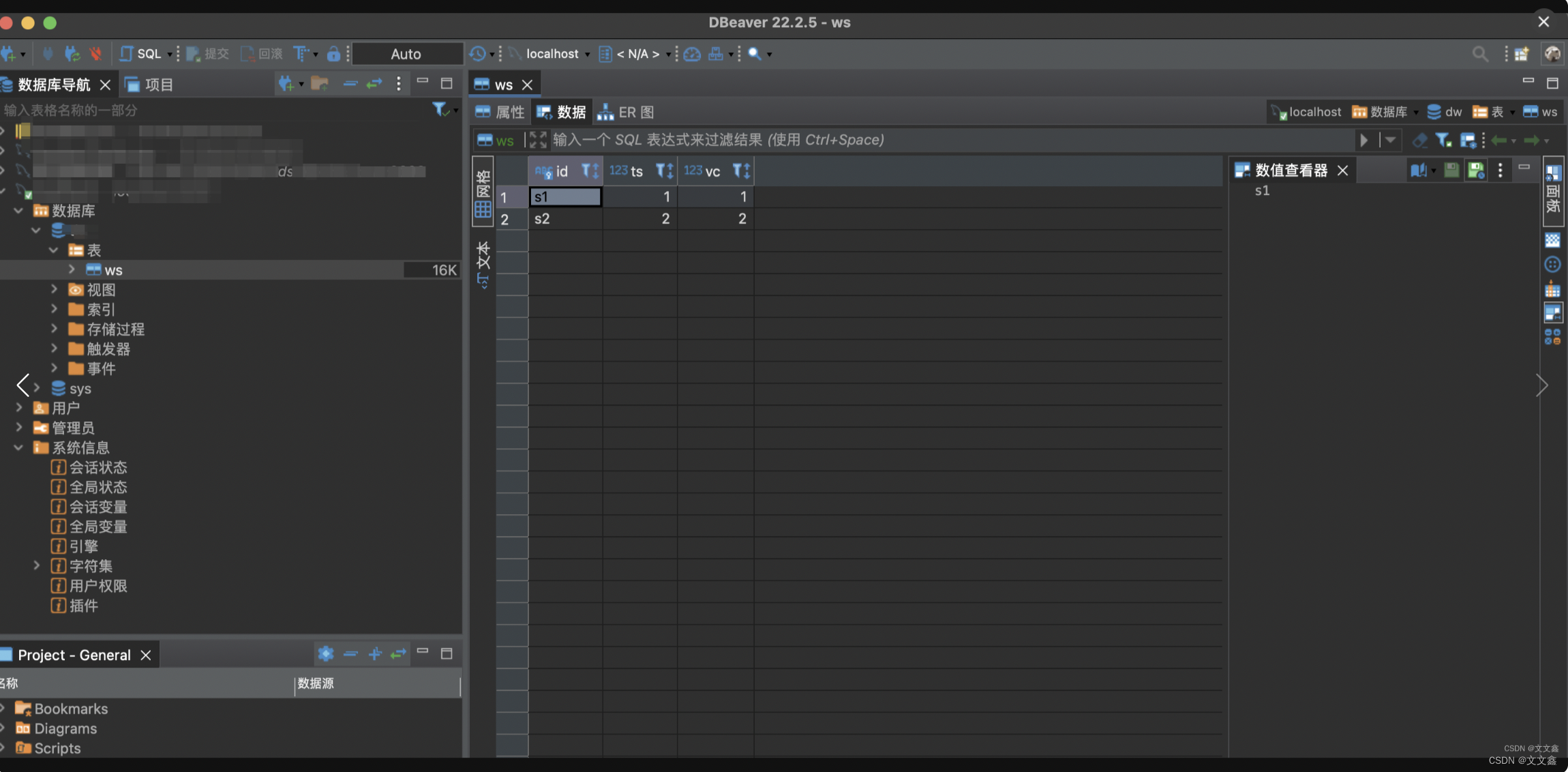
Flink将数据写入MySQL(JDBC)
一、写在前面 在实际的生产环境中,我们经常会把Flink处理的数据写入MySQL、Doris等数据库中,下面以MySQL为例,使用JDBC的方式将Flink的数据实时数据写入MySQL。 二、代码示例 2.1 版本说明 <flink.version>1.14.6</flink.version…...
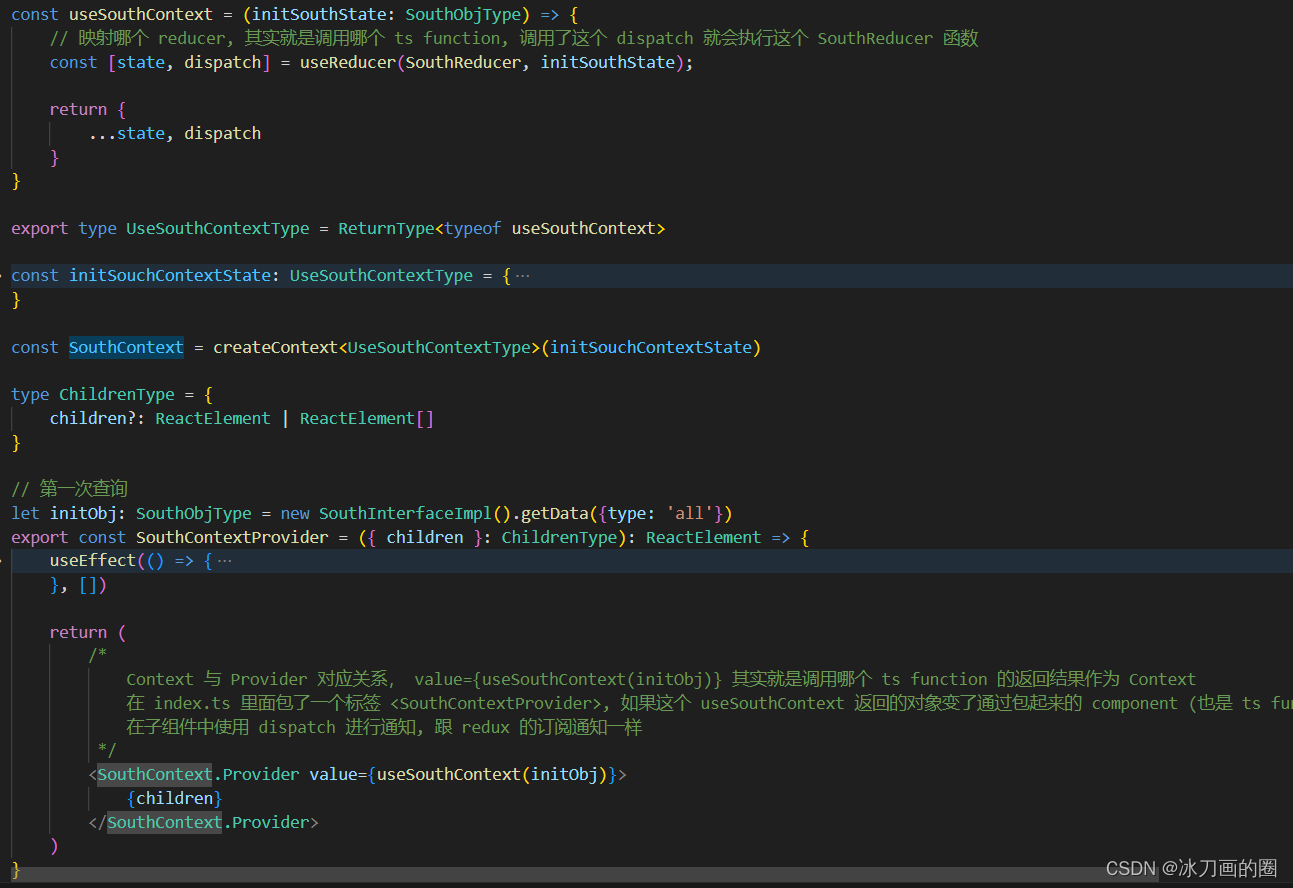
react-typescript-demo
1.使用 Context 来存储数据...

Alexon:在云原生环境中快速部署应用服务
Alexon是一个旨在快速部署WEB应用服务到分布式系统中的工具,适用于云原生环境。 Alexon由SymeCloud Limited(syme.dev) 发布,使用GNU Guile编写而成,支持函数编程概念。 SymeCloud 公司主要致力于 AI-Infra 方面的研发,从 OpenAI …...

5G技术在职业教育领域的应用:产生巨变的技术
5G技术在职业教育领域的应用:产生巨变的技术 职业教育领域正面临着前所未有的挑战和机遇。随着5G技术的快速发展和普及,其高速度、低延迟、大容量和连接数的特性给职业教育带来了革命性的改变。本文将深入探讨5G技术在职业教育领域的应用场景、技术原理和…...

【触想智能】工控一体机与5G物联网技术结合是未来发展趋势
工控一体机也叫工业电脑一体机,是工业应用非常重要的一种产品。目前,工控一体机在工业领域的应用已经非常普及,在繁忙的生产车间、数字化机床、自助服务终端设备等场景中,我们都有看到它的身影。 工控一体机应用的普及已经潜移默化…...
--lvgl - LVGL图像库)
LuatOS-SOC接口文档(air780E)--lvgl - LVGL图像库
lvgl.draw_mask_radius_param_t() 创建一个lv_draw_mask_radius_param_t 参数 无 返回值 返回值类型 解释 userdata lv_draw_mask_radius_param_t指针 例子 local radius lvgl.draw_mask_radius_param_t()lvgl.draw_mask_radius_param_t_free(radius) 释放一个lv_d…...
--lora2 - lora2驱动模块(支持多挂))
LuatOS-SOC接口文档(air780E)--lora2 - lora2驱动模块(支持多挂)
常量 常量 类型 解释 lora2.SLEEP number SLEEP模式 lora2.STANDBY number STANDBY模式 lora2.init(ic, loraconfig,spiconfig) lora初始化 参数 传入值类型 解释 string lora 型号,当前支持: llcc68 sx1268 table lora配置参数,与具体…...

WKWebView iOS17设置UserAgent
WKWebView 设置 user-agent 参考文档 之前设置 user-agent 都是通过设置NSUserDefaults来实现的,不过升级到了iOS17之后这个方式不好用了。 老的设置方式: [[NSUserDefaults standardUserDefaults] registerDefaults:dictionnary];目前看通过设置 we…...

持续集成部署-k8s-服务发现-Service
持续集成部署-k8s-服务发现-Service:配置讲解及基础命令 1. Service 简介2. 基础命令3. 基于 Service 访问外部服务4. 代理外部域名5. Endpoints 常用类型1. Service 简介 在K8s中,Service 是一种可以暴露一个或多个Pod的稳定的网络终点,从而形成逻辑上的应用服务单元,为服…...
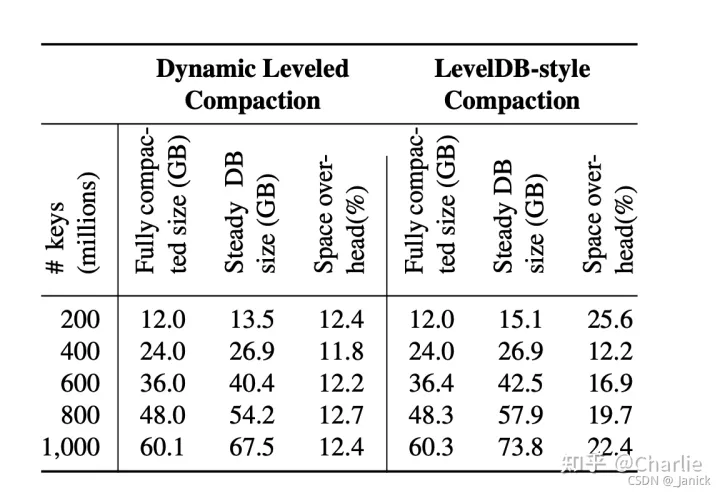
RocksDB基本架构与原理详解
Rocksdb Flink提供基于流的有状态计算,除了提供实时数据流的处理能力,还需要将计算产生的状态存储起来。 为了满足状态存取需求,提供了memory、flie system、rocksdb三种类型的状态存储机制。 memory存取高效单空间有限,且可用…...
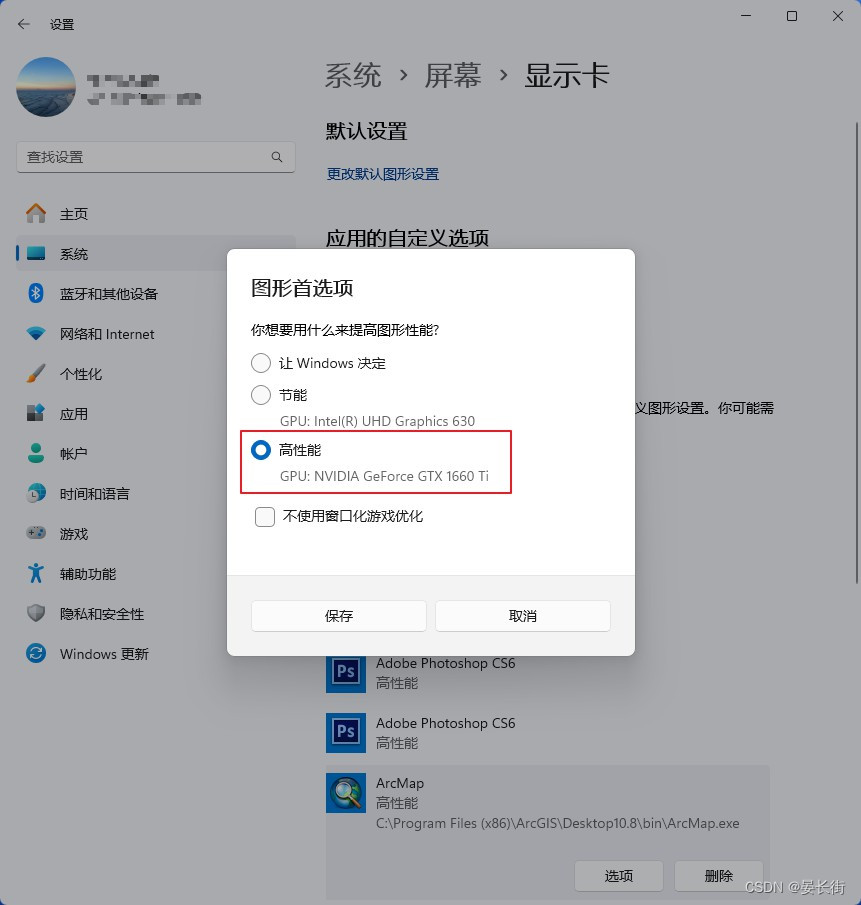
ArcGIS笔记12_ArcGIS搜索工具没法用?ArcGIS运行很慢很卡?
本文目录 前言Step 1 ArcGIS搜索工具没法用Step 2 ArcGIS运行很慢很卡 前言 这是笔者最近遇到的两个小问题,新换了台式机,安装上ArcGIS后发现搜索工具没法用,而且感觉还不如原来笔记本运行的流畅,加载图层很慢,编辑要…...

【VictoriaMetrics】单机版配置
为方便查看,释义都已翻译成中文,本文配置基于VictoriaMetrics 1.87.1版本 bigMergeConcurrencyint用于大合并的最大 CPU 核数。设置为 0 时使用默认值cacheExpireDuration30m0s...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...