4. 寻找两个正序数组的中位数
1. 题目
见 寻找两个正序数组的中位数
2. 解题思路
首先一看到题目说是正序数组,且时间复杂度要求在对数级别,所以自然想到了双指针中的二分法。

首先来看一下,假设输入是这两个数组,那么将其逻辑合并成一个大数组的话,分界线左边为大数组的左边,右边同理。这个数组又是升序的,且原来的两个数组是升序的(即L1<=R1& L2<=R2)。所以在大数组中,L1<=R2 & L2<=R1
所以这里就得到了第一个约束:切割后的中位线要满足交叉小于等于。
然后大数组的中位数呢,就是从中位数左边选择一个大的数字(Max(L1,L2))和右边选一个小的数字(Min(R1,R2))来进行计算。
上面的情况是刚好属于一个逻辑合并数组并且划分中位线后 满足交叉小于的情况,假如像下图划分中位线后不满足交叉小于呢?

因为L2>R1了,所以我们右移R1,直到比L2大,满足交叉小于等于。

这个时候会奇怪了,为什么要移动nums2的中位线?
因为此时我们做了一个逻辑合并数组的设想,所以整个大数组中位线两边的元素应该尽量保持相同。
R1移动后nums1中位线左边有5个元素,所以同理移动nums2的中位线,让它的右边也有5个元素。
另外需要注意的是:
1、我们默认只对nums1进行操作,由nums1的操作计算出对nums2的操作。比如 假如不符合交叉小于等于,那么我们就移动nums1的中位线,然后由公式算出nums2的中位线即可。
2、当数组为奇数的时候我们默认把中位线划分在右边一点(左边也是可以的)
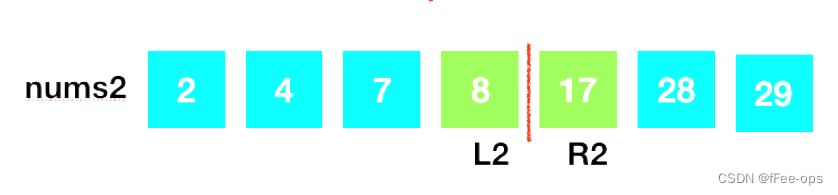
上面说的是两个数组都是偶数的情况,假如有个数字为奇数呢?

因为数组是有序的,且满足交叉小于等于,且奇数数组的中位数都是划分在右边的(我们约定的),单拎出来nums2看的话,中位数是中位线左边的那个。所以最后逻辑合并大数组了,中位数只要在大数组中位线左边取偏大的就行了。也就是max(L1,L2)
3. 代码
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {//保持数组长度小的在前面,节省性能if (nums1.length > nums2.length) {return findMedianSortedArrays(nums2, nums1);}int m = nums1.length;int n = nums2.length;int left = 0, right = m;int median1 = 0, median2 = 0;while (left <= right) {//确定第一个数组的分割线median1 = (left + right) / 2;//确定第二个数组的分割线median2 = (m + n + 1) / 2 - median1;//数组1中位分割线左边的数int L1= (median1 == 0 ? Integer.MIN_VALUE : nums1[median1 - 1]);//数组1中位分割线右边的数int R1= (median1 == m ? Integer.MAX_VALUE : nums1[median1]);//数组2中位分割线左边的数int L2= (median2 == 0 ? Integer.MIN_VALUE : nums2[median2 - 1]);//数组2中位分割线右边的数int R2= (median2 == n ? Integer.MAX_VALUE : nums2[median2]);int nums_j = (median2 == n ? Integer.MAX_VALUE : nums2[median2]);if (L1 > R2) {//不符合交叉小于等于 继续二分(左移中位线)right = median1-1;} else if (L2 > R1) {//不符合交叉小于等于 继续二分(右移中位线)left = median1 + 1;} else {//将所有的数合并后,如果是偶数个数,中位数是中间两个数的平均值,如果是奇数个数,中位数是大的数return (m + n) % 2 == 0 ? (Math.max(L1, L2) + Math.min(R1, R2)) / 2.0 : Math.max(L1, L2);}}return 0.0;}}
相关文章:

4. 寻找两个正序数组的中位数
1. 题目 见 寻找两个正序数组的中位数 2. 解题思路 首先一看到题目说是正序数组,且时间复杂度要求在对数级别,所以自然想到了双指针中的二分法。 首先来看一下,假设输入是这两个数组,那么将其逻辑合并成一个大数组的话&#x…...

Stable Diffusion AI绘图
提示词: masterpiece, best quality, 1girl, (anime), (manga), (2D), half body, perfect eyes, both eyes are the same, Global illumination, soft light, dream light, digital painting, extremely detailed CGI anime, hd, 2k, 4k background 反向提示词&…...

MR混合现实情景实训教学系统在旅游管理专业中的应用
在旅游管理专业中,MR混合现实情景实训教学系统的主要应用包括但不限于以下几个方面: 1. 实地考察的替代:对于一些无法实地考察的景点或设施,学生可以通过MR系统进行虚拟参观,从而了解其实际情况。这不仅可以减少时间和…...

CentOS 使用线程库Pthread 库
1、Pthread 库说明 pthread 库是Linux系统默认线程库。 在Linux 系统环境中,编辑C/C程序使用pthread 库,需要添加对应的头文件,并链接pthread库。 #include<pthread.h> 2、Pthread 库核心方法 pthread_create 函数定义࿱…...

#力扣:LCP 01. 猜数字@FDDLC
LCP 01. 猜数字 - 力扣(LeetCode) 一、Java class Solution {public int game(int[] guess, int[] answer) {int cnt0;for(int i0;i<3;i){if(guess[i]answer[i])cnt;}return cnt;} }...

kafka丢数据的原因
目录 背景kafkaClient代码消息丢失的可能原因broker is downRD_KAFKA_MSG_SIZE_TOO_LARGE分区问题Kafka Broker的处理能力无法跟上,可能会出现以下情况 Some基础知识补充 背景 采用的client是librdkafka,在producerClient Send的数据时候发现会有数据丢…...

音视频编解码技术学习笔记
音视频编解码技术是音视频处理领域的重要部分,涉及到对原始音视频数据的压缩、编码和解码。以下是音视频编解码技术的一些要点和难点: 要点: 压缩技术 音视频编解码的核心是对原始音视频数据进行压缩,以减小文件大小和传输带宽…...

[C#基础训练]FoodRobot食品管理部分代码-1
代码参考: using System;namespace FoodRobotDemo { public class FoodRobot{private int[] foodCountArr;private string[] foodNameArr;public FoodRobot(){foodCountArr new int[3];foodNameArr new string[3] {"航天","航空","宇航" };}…...

YModem协议总结
《YModem协议总结》 目录 第1章 YModem协议简介 4 1.1 基本介绍 4 1.2 YModem基本介绍 4 第2章 YModem传输协议 5 2.1 起始帧的数据格式 5 2.2 数据帧的数据格式 5 2.3 结束帧数据结构 6 2.4 文件传输过程 6 2.5 CRC的计算 7 附录A 附录 8 A.1 附录 8 第1章 YModem协议简…...
ElasticSearch(ES)8.1及Kibana在docker环境下如何安装
ES基本信息介绍 Elasticsearch(简称ES)是一个开源的分布式搜索和分析引擎,最初由Elastic公司创建。它属于Elastic Stack(ELK Stack)的核心组件之一,用于实时地存储、检索和分析大量数据。 以下是Elastics…...
常用Win32 API的简单介绍
目录 前言: 控制控制台程序窗口的指令: system函数: COORD函数: GetStdHandle函数: GetConsoleCursorInfo函数: CONSOLE_CURSOR_INFO函数: SetConsoleCursorInfo函数: SetC…...
VM及WindowsServer安装
目录 一.操作系统的简介及常用的操作系统 二.windows的安装 安装VMWare虚拟机 注意点一 编辑 注意点二 三.安装配置Windows Server 2012 R2 四、虚拟机的环境配置及连接 1. 主机连接虚拟机 2. 虚拟机环境配置及共享 3. 环境配置 一.操作系统的简介及常用的操作系…...

操作系统【OS】调度算法对比图
FCFS SJF 高响应比 时间片轮转 多级反馈队列 可抢占? √ √ √ 队列内算法不一定 不可抢占? √ √ √ 队列内算法不一定 特点&优点 公平实现简单有利于长作业不利于短作业有利于CPU繁忙作业不利于IO繁忙作业 因为CPU繁忙型进程即…...
:视频黑屏)
音视频开发常见问题(五):视频黑屏
摘要 本文介绍了视频黑屏的可能原因和解决方案。主要原因包括用户主动关闭视频、网络问题和渲染问题。解决方案包括优化网络稳定性、确保视频渲染视图设置正确、提供清晰的提示、实时监测网络质量、使用详细的日志系统、开启视频预览功能、使用视频流回调、处理编解码问题、处…...

力扣 第 368 场周赛
2908. 元素和最小的山形三元组 I 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 : i < j < k nums[i] < nums[j] 且 nums[k] < nums[j] 请你找出 nums 中 元素和最小 的…...
)
文件的常用操作(读取压缩文件、解压、删除)
背景:最近做一个腾讯 cos 桶 文件的读写与本地数据库查询等操作 Retrofit 中文件下载的可以添加 Streaming StreamingGETObservable<ResponseBody> downloadCosFile(Url String downloadUrl);Streaming 的作用: 注解通常用于指示Retrofit或其他HTT…...

Simulation Studio - TRNSYS
简单记录一下最近学习 Simulation Studio的一些经历。 在学习之初,参考了一些大佬们的文章: Fortran学习笔记——1.基本内容 - 知乎 但是我主要的目的是使用Simulation Studio(下文用SS代替)编译自己的组件,看到Sim…...

python实现串口通信
python实现串口通信是一件简单的事情,只要通过pyserial模块就可以实现。 一、串口通信 1、什么是串口通信? 串口通信是一种通过串行接口(Serial Port)进行数据传输的通信方式。在串口通信中,数据位按顺序一位一位地传…...
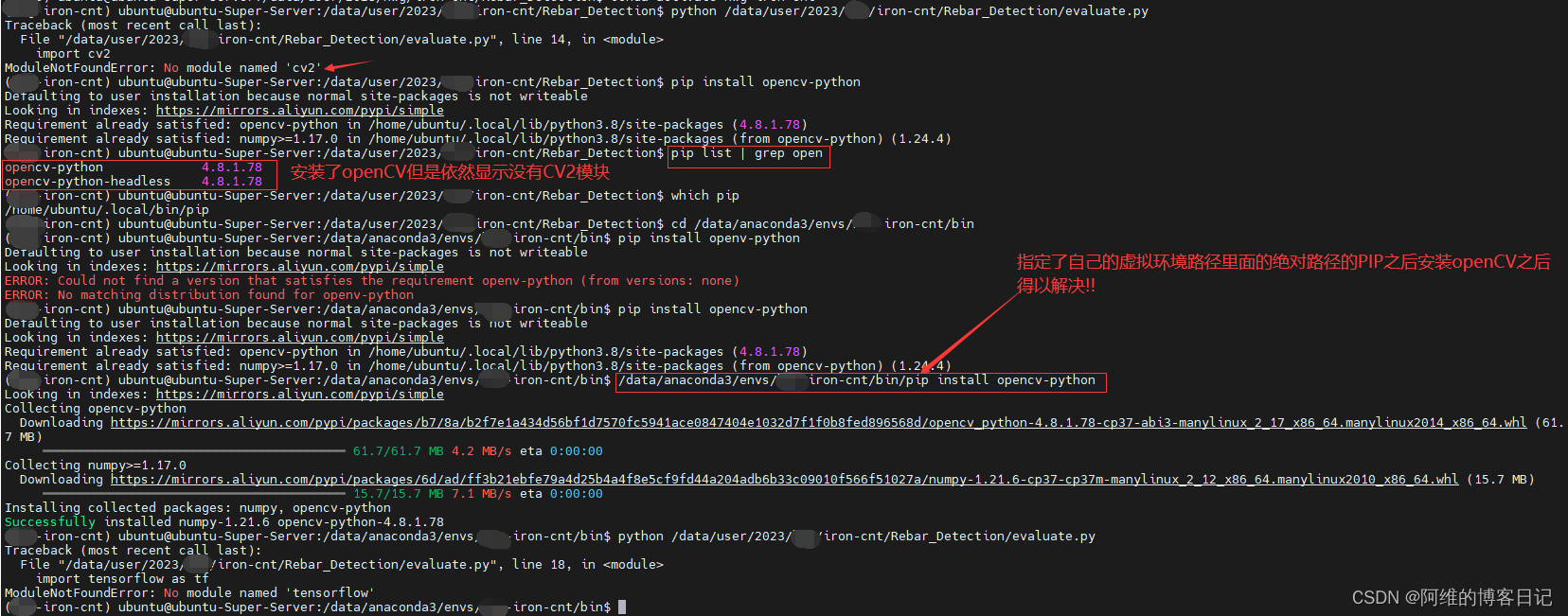
No module named ‘cv2’ 解决方法
目录 解决方案1解决方案2 解决方案1 一般情况下的解决方案 在自己的虚拟环境里面安装就行 pip install opencv-python解决方案2 但是我遇到的情况没有这么简单,我使用了pip list | grep open 搜索含有open字样的opencv的包,结果显示已经安装了 我直接进入我的自定义的虚拟…...
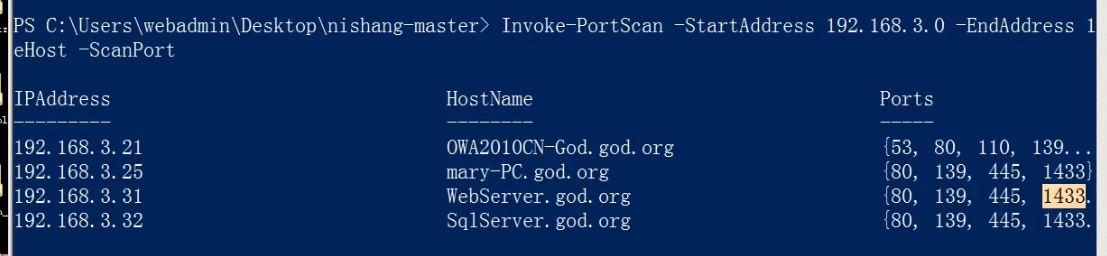
65、内网安全-域环境工作组局域网探针方案
目录 案例1-基本信息收集操作演示案例2-网络信息收集操作演示案例3-用户信息收集操作演示案例4-凭据信息收集操作演示案例5-探针主机域控架构服务操作演示涉及资源 我们攻击内网一般是借助web攻击,直接进去,然后再去攻击内网,那么攻击的对象一…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
