《视觉SLAM十四讲》公式推导(三)
文章目录
- CH3-8 证明旋转后的四元数虚部为零,实部为罗德里格斯公式结果
- CH4 李群与李代数
- CH4-1 SO(3) 上的指数映射
- CH4-2 SE(3) 上的指数映射
- CH4-3 李代数求导
- 对极几何:本质矩阵奇异值分解
- 矩阵内积和迹
CH3-8 证明旋转后的四元数虚部为零,实部为罗德里格斯公式结果
前面已经推导过
v ′ = p v p ∗ = p v p − 1 v'=pvp^*=pvp^{-1} v′=pvp∗=pvp−1
其中, v = [ 0 , v ⃗ ] v=[0,\vec{v}] v=[0,v], p = [ cos θ 2 , sin θ 2 u ⃗ ] p=[\cos\frac{\theta}{2},\sin\frac{\theta}{2}\vec{u}] p=[cos2θ,sin2θu],代入上式
v ′ = p v p ∗ = [ cos θ 2 , sin θ 2 u ⃗ ] [ 0 , v ⃗ ] [ cos θ 2 , − sin θ 2 u ⃗ ] = [ 0 − sin θ 2 u ⃗ ⋅ v ⃗ , cos θ 2 v ⃗ + 0 + sin θ 2 u ⃗ × v ⃗ ] [ cos θ 2 , − sin θ 2 u ⃗ ] = [ − sin θ 2 u ⃗ ⋅ v ⃗ , cos θ 2 v ⃗ + sin θ 2 u ⃗ × v ⃗ ] [ cos θ 2 , − sin θ 2 u ⃗ ] (3-8-1) \begin{aligned} v'&=pvp^* \\ &=[\cos\frac{\theta}{2},\sin\frac{\theta}{2}\vec{u}][0,\vec{v}][\cos\frac{\theta}{2},-\sin\frac{\theta}{2}\vec{u}] \\ &=[0-\sin\frac{\theta}{2}\vec{u}\cdot\vec{v},\cos\frac{\theta}{2}\vec{v}+0+\sin\frac{\theta}{2}\vec{u}\times\vec{v}][\cos\frac{\theta}{2},-\sin\frac{\theta}{2}\vec{u}] \\ &=[-\sin\frac{\theta}{2}\vec{u}\cdot\vec{v},\cos\frac{\theta}{2}\vec{v}+\sin\frac{\theta}{2}\vec{u}\times\vec{v}][\cos\frac{\theta}{2},-\sin\frac{\theta}{2}\vec{u}] \end{aligned} \tag{3-8-1} v′=pvp∗=[cos2θ,sin2θu][0,v][cos2θ,−sin2θu]=[0−sin2θu⋅v,cos2θv+0+sin2θu×v][cos2θ,−sin2θu]=[−sin2θu⋅v,cos2θv+sin2θu×v][cos2θ,−sin2θu](3-8-1)
分别计算实部和虚部
R e = − sin θ 2 cos θ 2 u ⃗ ⋅ v ⃗ + ( cos θ 2 v ⃗ + sin θ 2 u ⃗ × v ⃗ ) ⋅ sin θ 2 u ⃗ = − sin θ 2 cos θ 2 u ⃗ ⋅ v ⃗ + cos θ 2 sin θ 2 u ⃗ ⋅ v ⃗ + sin θ 2 ( u ⃗ × v ⃗ ) ⋅ u ⃗ = 0 + 0 = 0 (3-8-2) \begin{aligned} \mathrm{Re}&=-\sin\frac{\theta}{2}\cos\frac{\theta}{2}\vec{u}\cdot\vec{v}+(\cos\frac{\theta}{2}\vec{v}+\sin\frac{\theta}{2}\vec{u}\times\vec{v})\cdot\sin\frac{\theta}{2}\vec{u}\\ &=-\sin\frac{\theta}{2}\cos\frac{\theta}{2}\vec{u}\cdot\vec{v}+\cos\frac{\theta}{2}\sin\frac{\theta}{2}\vec{u}\cdot\vec{v}+\sin\frac{\theta}{2}(\vec{u}\times\vec{v})\cdot\vec{u}\\ &=0+0 \\ &=0 \end{aligned} \tag{3-8-2} Re=−sin2θcos2θu⋅v+(cos2θv+sin2θu×v)⋅sin2θu=−sin2θcos2θu⋅v+cos2θsin2θu⋅v+sin2θ(u×v)⋅u=0+0=0(3-8-2)
I m = ( − sin θ 2 u ⃗ ⋅ v ⃗ ) ⋅ ( − sin θ 2 u ⃗ ) + ( cos θ 2 v ⃗ + sin θ 2 u ⃗ × v ⃗ ) cos θ 2 + ( cos θ 2 v ⃗ + sin θ 2 u ⃗ × v ⃗ ) × ( − sin θ 2 u ⃗ ) (3-8-3) \begin{aligned} \mathrm{Im}&=(-\sin\frac{\theta}{2}\vec{u}\cdot\vec{v})\cdot(-\sin\frac{\theta}{2}\vec{u})+(\cos\frac{\theta}{2}\vec{v}+\sin\frac{\theta}{2}\vec{u}\times\vec{v})\cos\frac{\theta}{2} \\ &+(\cos\frac{\theta}{2}\vec{v}+\sin\frac{\theta}{2}\vec{u}\times\vec{v})\times(-\sin\frac{\theta}{2}\vec{u}) \end{aligned} \tag{3-8-3} Im=(−sin2θu⋅v)⋅(−sin2θu)+(cos2θv+sin2θu×v)cos2θ+(cos2θv+sin2θu×v)×(−sin2θu)(3-8-3)
我们希望将其写成矩阵乘法形式。
先证明公式: a ⃗ × ( b ⃗ × c ⃗ ) = ( a ⃗ ⋅ c ⃗ ) ⋅ b ⃗ − ( a ⃗ ⋅ b ⃗ ) ⋅ c ⃗ \vec{a}\times(\vec{b}\times\vec{c})=(\vec{a}\cdot\vec{c})\cdot\vec{b}-(\vec{a}\cdot\vec{b})\cdot\vec{c} a×(b×c)=(a⋅c)⋅b−(a⋅b)⋅c。
证明:
a ⃗ × b ⃗ = a ∧ b = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] [ b 1 b 2 b 3 ] = △ T a b (3-8-4) \begin{aligned} \vec{a}\times\vec{b}&=\boldsymbol{a}^{\wedge}\boldsymbol{b} \\ &=\left[\begin{array}{c} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{array}\right]\left[\begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array}\right]\stackrel{\bigtriangleup}=\boldsymbol{T}_a\boldsymbol{b} \end{aligned} \tag{3-8-4} a×b=a∧b= 0a3−a2−a30a1a2−a10 b1b2b3 =△Tab(3-8-4)
那么(矩阵乘法满足结合律)
a ⃗ × ( b ⃗ × c ⃗ ) = ( T a T b ) c = T a T b c \vec{a}\times(\vec{b}\times\vec{c})=(\boldsymbol{T}_a\boldsymbol{T}_b)\boldsymbol{c}=\boldsymbol{T}_a\boldsymbol{T}_b\boldsymbol{c} a×(b×c)=(TaTb)c=TaTbc
而
T a T b = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] [ 0 − b 3 b 2 b 3 0 − b 1 − b 2 b 1 0 ] = [ − a 3 b 3 − a 2 b 2 a 2 b 1 a 3 b 1 a 1 b 2 − a 3 b 3 − a 1 b 1 a 3 b 2 a 1 b 3 a 2 b 3 − a 2 b 2 − a 1 b 1 ] = − ( a ⃗ ⋅ b ⃗ ) I + b a T \begin{aligned} \boldsymbol{T}_a\boldsymbol{T}_b&=\left[\begin{array}{c} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{array}\right]\left[\begin{array}{c} 0 & -b_3 & b_2 \\ b_3 & 0 & -b_1 \\ -b_2 & b_1 & 0 \end{array}\right] \\ &=\left[\begin{array}{c} -a_3b_3-a_2b_2 & a_2b_1 & a_3b_1 \\ a_1b_2 & -a_3b_3-a_1b_1 & a_3b_2 \\ a_1b_3 & a_2b_3 & -a_2b_2 -a_1b_1 \end{array}\right]\\ &=-(\vec{a}\cdot\vec{b})\boldsymbol{I}+\boldsymbol{b}\boldsymbol{a}^{\mathrm{T}} \end{aligned} TaTb= 0a3−a2−a30a1a2−a10 0b3−b2−b30b1b2−b10 = −a3b3−a2b2a1b2a1b3a2b1−a3b3−a1b1a2b3a3b1a3b2−a2b2−a1b1 =−(a⋅b)I+baT
则(用到了矩阵结合律)
a ⃗ × ( b ⃗ × c ⃗ ) = T a T b c = ( − ( a ⃗ ⋅ b ⃗ ) I + b a T ) c = − ( a ⃗ ⋅ b ⃗ ) c + b ( a T c ) = − ( a ⃗ ⋅ b ⃗ ) c + ( a ⃗ ⋅ c ⃗ ) b (3-8-5) \begin{aligned} \vec{a}\times(\vec{b}\times\vec{c})=\boldsymbol{T}_a\boldsymbol{T}_b\boldsymbol{c}&=(-(\vec{a}\cdot\vec{b})\boldsymbol{I}+\boldsymbol{b}\boldsymbol{a}^{\mathrm{T}})\boldsymbol{c} \\ &=-(\vec{a}\cdot\vec{b})\boldsymbol{c}+\boldsymbol{b}(\boldsymbol{a}^{\mathrm{T}}\boldsymbol{c}) \\ &=-(\vec{a}\cdot\vec{b})\boldsymbol{c}+(\vec{a}\cdot\vec{c})\boldsymbol{b} \end{aligned} \tag{3-8-5} a×(b×c)=TaTbc=(−(a⋅b)I+baT)c=−(a⋅b)c+b(aTc)=−(a⋅b)c+(a⋅c)b(3-8-5)
同理可证
( a ⃗ × b ⃗ ) × c ⃗ = ( a ⃗ ⋅ c ⃗ ) b − ( b ⃗ ⋅ c ⃗ ) a (3-8-6) (\vec{a}\times\vec{b})\times\vec{c}=(\vec{a}\cdot\vec{c})\boldsymbol{b}-(\vec{b}\cdot\vec{c})\boldsymbol{a} \tag{3-8-6} (a×b)×c=(a⋅c)b−(b⋅c)a(3-8-6)
证毕。
下面继续推导式(3-8-3)
I m = sin 2 θ 2 u ⃗ ⋅ v ⃗ ⋅ u ⃗ + cos 2 θ 2 v ⃗ + sin θ 2 cos θ 2 u ⃗ × v ⃗ − sin θ 2 cos θ 2 v ⃗ × u ⃗ − sin 2 θ 2 u ⃗ × v ⃗ × u ⃗ = sin 2 θ 2 ( u ⃗ ⋅ v ⃗ ) ⋅ u ⃗ + cos 2 θ 2 v ⃗ + sin θ u ⃗ × v ⃗ − sin 2 θ 2 [ ( u ⃗ ⋅ u ⃗ ) v − ( v ⃗ ⋅ u ⃗ ) u ] = sin 2 θ 2 ( u ⃗ ⋅ v ⃗ ) ⋅ u ‾ + cos 2 θ 2 v + sin θ u ⃗ × v ⃗ − sin 2 θ 2 v + sin 2 θ 2 ( v ⃗ ⋅ u ⃗ ) u ‾ = cos θ v + 2 sin 2 θ 2 ( v ⃗ ⋅ u ⃗ ) u + sin θ u ⃗ × v ⃗ = cos θ v + ( 1 − cos θ ) ( v ⃗ ⋅ u ⃗ ) u + sin θ u ⃗ × v ⃗ (3-8-7) \begin{aligned} \mathrm{Im}&=\sin^2\frac{\theta}{2}\vec{u}\cdot\vec{v}\cdot\vec{u}+\cos^2\frac{\theta}{2}\vec{v}+\sin\frac{\theta}{2}\cos\frac{\theta}{2}\vec{u}\times\vec{v}-\sin\frac{\theta}{2}\cos\frac{\theta}{2}\vec{v}\times\vec{u}-\sin^2\frac{\theta}{2}\vec{u}\times\vec{v}\times\vec{u} \\ &=\sin^2\frac{\theta}{2}(\vec{u}\cdot\vec{v})\cdot\vec{u}+\cos^2\frac{\theta}{2}\vec{v}+\sin\theta\vec{u}\times\vec{v}-\sin^2\frac{\theta}{2}[(\vec{u}\cdot\vec{u})\boldsymbol{v}-(\vec{v}\cdot\vec{u})\boldsymbol{u}] \\ &=\underline{\sin^2\frac{\theta}{2}(\vec{u}\cdot\vec{v})\cdot\boldsymbol{u}}+\cos^2\frac{\theta}{2}\boldsymbol{v}+\sin\theta\vec{u}\times\vec{v}-\sin^2\frac{\theta}{2}\boldsymbol{v}+\underline{\sin^2\frac{\theta}{2}(\vec{v}\cdot\vec{u})\boldsymbol{u}} \\ &=\cos\theta\boldsymbol{v}+2\sin^2\frac{\theta}{2}(\vec{v}\cdot\vec{u})\boldsymbol{u}+\sin\theta\vec{u}\times\vec{v} \\ &=\cos\theta\boldsymbol{v}+(1-\cos\theta)(\vec{v}\cdot\vec{u})\boldsymbol{u}+\sin\theta\vec{u}\times\vec{v} \end{aligned} \tag{3-8-7} Im=sin22θu⋅v⋅u+cos22θv+sin2θcos2θu×v−sin2θcos2θv×u−sin22θu×v×u=sin22θ(u⋅v)⋅u+cos22θv+sinθu×v−sin22θ[(u⋅u)v−(v⋅u)u]=sin22θ(u⋅v)⋅u+cos22θv+sinθu×v−sin22θv+sin22θ(v⋅u)u=cosθv+2sin22θ(v⋅u)u+sinθu×v=cosθv+(1−cosθ)(v⋅u)u+sinθu×v(3-8-7)
注意: u ⃗ \vec{u} u 是单位向量,故 u ⃗ ⋅ u ⃗ = 1 \vec{u}\cdot\vec{u}=1 u⋅u=1。
也就是拉格朗日公式结果。证毕。
CH4 李群与李代数
CH4-1 SO(3) 上的指数映射
将指数函数 e x e^x ex 在 x = 0 x=0 x=0 处泰勒展开,即
e x = 1 + x + 1 2 ! x 2 + 1 3 ! x 3 + . . . + 1 n ! x n = ∑ n = 0 ∞ x n n ! (4-1-1) \begin{aligned} e^x &= 1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+...+\frac{1}{n!}x^n \\ &=\sum_{n=0}^{\infty}\frac{x^n}{n!} \end{aligned} \tag{4-1-1} ex=1+x+2!1x2+3!1x3+...+n!1xn=n=0∑∞n!xn(4-1-1)
将矩阵 A \boldsymbol{A} A 代入上式, 则
e A = ∑ n = 0 ∞ A n n ! e^{\boldsymbol{A}}=\sum_{n=0}^{\infty}\frac{\boldsymbol{A}^n}{n!} eA=n=0∑∞n!An
同样的,也有
e ϕ ∧ = ∑ n = 0 ∞ ( ϕ ∧ ) n n ! (4-1-2) e^{\boldsymbol{\phi}^{\wedge}}=\sum_{n=0}^{\infty}\frac{(\boldsymbol{\phi}^{\wedge})^n}{n!} \tag{4-1-2} eϕ∧=n=0∑∞n!(ϕ∧)n(4-1-2)
令 ϕ = θ a \boldsymbol{\phi}=\theta\boldsymbol{a} ϕ=θa, θ \theta θ为模长, a \boldsymbol{a} a 为单位方向向量。则上式可写为
e ( θ a ) ∧ = ∑ n = 0 ∞ ( θ a ∧ ) n n ! e^{\boldsymbol({\theta\boldsymbol{a}})^{\wedge}}=\sum_{n=0}^{\infty}\frac{(\theta\boldsymbol{a}^{\wedge})^n}{n!} e(θa)∧=n=0∑∞n!(θa∧)n
我们知道
a ∧ = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] \boldsymbol{a}^{\wedge}=\left[\begin{array}{c} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{array}\right] a∧= 0a3−a2−a30a1a2−a10
则
a ∧ a ∧ = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] = [ − a 3 2 − a 2 2 a 1 a 2 a 1 a 3 a 1 a 2 − a 3 2 − a 1 2 a 2 a 3 a 1 a 3 a 2 a 3 − a 2 2 − a 1 2 ] (4-1-3) \begin{aligned} \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}&=\left[\begin{array}{c} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{array}\right]\left[\begin{array}{c} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{array}\right] \\ &=\left[\begin{array}{c} -a_3^2-a_2^2 & a_1a_2 & a_1a_3 \\ a_1a_2 & -a_3^2-a_1^2 & a_2a_3 \\ a_1a_3 & a_2a_3 & -a_2^2-a_1^2 \end{array}\right] \end{aligned} \tag{4-1-3} a∧a∧= 0a3−a2−a30a1a2−a10 0a3−a2−a30a1a2−a10 = −a32−a22a1a2a1a3a1a2−a32−a12a2a3a1a3a2a3−a22−a12 (4-1-3)
因为 a \boldsymbol{a} a 是单位向量,则有 a 1 2 + a 2 2 + a 3 2 = 1 a_1^2+a_2^2+a_3^2=1 a12+a22+a32=1,可得
a a T − I = [ a 1 a 2 a 3 ] [ a 1 a 2 a 3 ] = [ a 1 2 a 1 a 2 a 1 a 3 a 2 a 1 a 2 2 a 2 a 3 a 1 a 3 a 2 a 3 a 3 2 ] − [ 1 0 0 0 1 0 0 0 1 ] = [ − a 3 2 − a 2 2 a 1 a 2 a 1 a 3 a 1 a 2 − a 3 2 − a 1 2 a 2 a 3 a 1 a 3 a 2 a 3 − a 2 2 − a 1 2 ] = a ∧ a ∧ (4-1-4) \begin{aligned} \boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{I}=\left[\begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array}\right]\left[\begin{array}{ccc} a_1 & a_2 & a_3 \end{array}\right] &=\left[\begin{array}{c} a_1^2 & a_1a_2 & a_1a_3 \\ a_2a_1 & a_2^2 & a_2a_3 \\ a_1a_3 & a_2a_3 & a_3^2 \end{array}\right]- \left[\begin{array}{c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \\ &=\left[\begin{array}{c} -a_3^2-a_2^2 & a_1a_2 & a_1a_3 \\ a_1a_2 & -a_3^2-a_1^2 & a_2a_3 \\ a_1a_3 & a_2a_3 & -a_2^2-a_1^2 \end{array}\right] \\ &=\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge} \end{aligned} \tag{4-1-4} aaT−I= a1a2a3 [a1a2a3]= a12a2a1a1a3a1a2a22a2a3a1a3a2a3a32 − 100010001 = −a32−a22a1a2a1a3a1a2−a32−a12a2a3a1a3a2a3−a22−a12 =a∧a∧(4-1-4)
a ∧ a ∧ a ∧ = [ − a 3 2 − a 2 2 a 1 a 2 a 1 a 3 a 1 a 2 − a 3 2 − a 1 2 a 2 a 3 a 1 a 3 a 2 a 3 − a 2 2 − a 1 2 ] [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] = [ 0 a 2 2 a 3 + a 3 3 + a 1 2 a 3 − a 2 3 − a 2 a 3 2 − a 1 a 2 2 − a 1 2 a 3 − a 3 3 − a 1 2 a 3 0 a 1 a 2 2 + a 1 3 + a 1 a 3 2 a 2 a 3 2 + a 1 2 a 2 + a 2 3 − a 1 a 3 2 − a 1 3 − a 1 a 2 2 0 ] \begin{aligned} \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}&=\left[\begin{array}{c} -a_3^2-a_2^2 & a_1a_2 & a_1a_3 \\ a_1a_2 & -a_3^2-a_1^2 & a_2a_3 \\ a_1a_3 & a_2a_3 & -a_2^2-a_1^2 \end{array}\right]\left[\begin{array}{c} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{array}\right] \\ &=\left[\begin{array}{c} 0 & a_2^2a_3+a_3^3+a_1^2a_3 & -a_2^3-a_2a_3^2-a_1a_2^2 \\ -a_1^2a_3-a_3^3-a_1^2a_3 & 0 & a_1a_2^2+a_1^3+a_1a_3^2 \\ a_2a_3^2+a_1^2a_2+a_2^3 & -a_1a_3^2-a_1^3-a_1a_2^2 & 0 \end{array}\right] \\ \end{aligned} a∧a∧a∧= −a32−a22a1a2a1a3a1a2−a32−a12a2a3a1a3a2a3−a22−a12 0a3−a2−a30a1a2−a10 = 0−a12a3−a33−a12a3a2a32+a12a2+a23a22a3+a33+a12a30−a1a32−a13−a1a22−a23−a2a32−a1a22a1a22+a13+a1a320
又 a 1 2 + a 2 2 + a 3 2 = 1 a_1^2+a_2^2+a_3^2=1 a12+a22+a32=1,上式写为
a ∧ a ∧ a ∧ = [ 0 a 3 − a 2 − a 3 0 a 1 a 2 − a 1 0 ] = − a ∧ (4-1-5) \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}=\left[\begin{array}{c} 0 & a_3 & -a_2 \\ -a_3 & 0 & a_1 \\ a_2 & -a_1 & 0 \end{array}\right]=-\boldsymbol{a}^{\wedge} \tag{4-1-5} a∧a∧a∧= 0−a3a2a30−a1−a2a10 =−a∧(4-1-5)
对式(4-1-2)
e ϕ ∧ = e ( θ a ) ∧ = ∑ n = 0 ∞ ( θ a ∧ ) n n ! = I + θ a ∧ + 1 2 ! θ 2 a ∧ a ∧ + 1 3 ! θ 3 a ∧ a ∧ a ∧ + 1 4 ! θ 4 a ∧ a ∧ a ∧ a ∧ + . . . = ( a a T − a ∧ a ∧ ) + θ a ∧ + 1 2 ! θ 2 a ∧ a ∧ − 1 3 ! θ 3 a ∧ − 1 4 ! θ 4 a ∧ a ∧ + . . . = a a T + ( θ − 1 3 ! θ 3 + 1 5 ! θ 5 + . . . ) a ∧ + ( − 1 + 1 2 ! θ 2 − 1 4 ! θ 4 + . . . ) a ∧ a ∧ = ( a ∧ a ∧ + I ) + sin θ a ∧ − cos θ ( a ∧ a ∧ ) = ( 1 − cos θ ) a ∧ a ∧ + I + sin θ a ∧ = ( 1 − cos θ ) ( a a T − I ) + I + sin θ a ∧ = a a T − I − cos θ a a T + cos θ I + I + sin θ a ∧ = cos θ I + ( 1 − cos θ ) a a T + sin θ a ∧ \begin{aligned} e^{\boldsymbol{\phi}^{\wedge}}=e^{\boldsymbol({\theta\boldsymbol{a}})^{\wedge}}&=\sum_{n=0}^{\infty}\frac{(\theta\boldsymbol{a}^{\wedge})^n}{n!} \\ &=\boldsymbol{I}+\theta\boldsymbol{a}^{\wedge}+\frac{1}{2!}\theta^2 \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+\frac{1}{3!}\theta^3 \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+\frac{1}{4!}\theta^4 \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+...\\ &=(\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge})+\theta\boldsymbol{a}^{\wedge}+\frac{1}{2!}\theta^2 \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}-\frac{1}{3!}\theta^3 \boldsymbol{a}^{\wedge}-\frac{1}{4!}\theta^4 \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+...\\ &=\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}+(\theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+...)\boldsymbol{a}^{\wedge}+(-1+\frac{1}{2!}\theta^2-\frac{1}{4!}\theta^4+...)\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\\ &=(\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+\boldsymbol{I})+\sin\theta \boldsymbol{a}^{\wedge}-\cos\theta(\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge})\\ &=(1-\cos\theta)\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+\boldsymbol{I}+\sin\theta \boldsymbol{a}^{\wedge} \\ &=(1-\cos\theta)(\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{I})+\boldsymbol{I}+\sin\theta \boldsymbol{a}^{\wedge}\\ &=\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{I}-\cos\theta\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}+\cos\theta\boldsymbol{I}+\boldsymbol{I}+\sin\theta \boldsymbol{a}^{\wedge}\\ &=\cos\theta\boldsymbol{I}+(1-\cos\theta)\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}+\sin\theta \boldsymbol{a}^{\wedge} \end{aligned} eϕ∧=e(θa)∧=n=0∑∞n!(θa∧)n=I+θa∧+2!1θ2a∧a∧+3!1θ3a∧a∧a∧+4!1θ4a∧a∧a∧a∧+...=(aaT−a∧a∧)+θa∧+2!1θ2a∧a∧−3!1θ3a∧−4!1θ4a∧a∧+...=aaT+(θ−3!1θ3+5!1θ5+...)a∧+(−1+2!1θ2−4!1θ4+...)a∧a∧=(a∧a∧+I)+sinθa∧−cosθ(a∧a∧)=(1−cosθ)a∧a∧+I+sinθa∧=(1−cosθ)(aaT−I)+I+sinθa∧=aaT−I−cosθaaT+cosθI+I+sinθa∧=cosθI+(1−cosθ)aaT+sinθa∧
于是得到李代数 ϕ \boldsymbol{\phi} ϕ 和旋转矩阵 R \boldsymbol{R} R 之间的映射关系,即
R = e ϕ ∧ = cos θ I + ( 1 − cos θ ) a a T + sin θ a ∧ (4-1-6) \boldsymbol{R}=e^{\boldsymbol{\phi}^{\wedge}}=\cos\theta\boldsymbol{I}+(1-\cos\theta)\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}+\sin\theta \boldsymbol{a}^{\wedge} \tag{4-1-6} R=eϕ∧=cosθI+(1−cosθ)aaT+sinθa∧(4-1-6)
也就是 罗德里格斯公式。
CH4-2 SE(3) 上的指数映射
已知李代数 ξ = [ ρ ϕ ] T ∈ R 6 \boldsymbol{\xi}=[\rho \quad \phi]^{\mathrm{T}}\in \boldsymbol{\mathbb{R}}^6 ξ=[ρϕ]T∈R6,它的反对称矩阵为
ξ ∧ = [ ϕ ∧ ρ 0 T 0 ] \boldsymbol{\xi}^{\wedge}=\left[\begin{array}{c} \phi^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right] ξ∧=[ϕ∧0Tρ0]
则李群为
T = exp ( ξ ∧ ) = [ ∑ n = 0 ∞ ( ϕ ∧ ) n n ! ∑ n = 0 ∞ ( ϕ ∧ ) n ( n + 1 ) ! ρ 0 T 0 ] ≜ [ R J ρ 0 T 1 ] (4-2-1) \begin{aligned} \boldsymbol{T}=\exp(\boldsymbol{\xi}^{\wedge})&=\left[\begin{array}{c} \sum_{n=0}^{\infty}\frac{(\boldsymbol{\phi}^{\wedge})^n}{n!} & \sum_{n=0}^{\infty}\frac{(\boldsymbol{\phi}^{\wedge})^n}{(n+1)!}\rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right] \\ &\triangleq \left[\begin{array}{c} \boldsymbol{R} & \boldsymbol{J}\rho \\ \boldsymbol{0}^{\mathrm{T}} & 1 \end{array}\right] \end{aligned} \tag{4-2-1} T=exp(ξ∧)=[∑n=0∞n!(ϕ∧)n0T∑n=0∞(n+1)!(ϕ∧)nρ0]≜[R0TJρ1](4-2-1)
下面开始证明
同样,假设 ϕ = θ a \boldsymbol{\phi}=\theta\boldsymbol{a} ϕ=θa, θ \theta θ为模长, a \boldsymbol{a} a为单位方向向量。将 exp ( ξ ∧ ) \exp(\boldsymbol{\xi}^{\wedge}) exp(ξ∧) 泰勒展开
exp ( ξ ∧ ) = 1 n ! ∑ n = 0 ∞ [ ϕ ∧ ρ 0 T 0 ] n = 1 n ! ∑ n = 0 ∞ [ θ a ∧ ρ 0 T 0 ] n (4-2-2) \exp(\boldsymbol{\xi}^{\wedge})=\frac{1}{n!}\sum_{n=0}^{\infty}\left[\begin{array}{c} \phi^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]^n=\frac{1}{n!}\sum_{n=0}^{\infty}\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]^n \tag{4-2-2} exp(ξ∧)=n!1n=0∑∞[ϕ∧0Tρ0]n=n!1n=0∑∞[θa∧0Tρ0]n(4-2-2)
当 n = 0 n=0 n=0 时,
1 0 ! [ ϕ ∧ ρ 0 T 0 ] 0 = I \frac{1}{0!}\left[\begin{array}{c} \phi^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]^0=\boldsymbol{I} 0!1[ϕ∧0Tρ0]0=I
当 n = 1 n=1 n=1 时,
1 1 ! [ θ a ∧ ρ 0 T 0 ] 1 = [ θ a ∧ ρ 0 T 0 ] \frac{1}{1!}\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]^1=\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right] 1!1[θa∧0Tρ0]1=[θa∧0Tρ0]
当 n = 2 n=2 n=2 时,
1 2 ! [ θ a ∧ ρ 0 T 0 ] [ θ a ∧ ρ 0 T 0 ] = [ ( θ a ∧ ) 2 θ a ∧ ρ 0 T 0 ] \frac{1}{2!}\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]=\left[\begin{array}{c} (\theta\boldsymbol{a}^{\wedge})^2 & \theta\boldsymbol{a}^{\wedge}\rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right] 2!1[θa∧0Tρ0][θa∧0Tρ0]=[(θa∧)20Tθa∧ρ0]
当 n = 3 n=3 n=3 时,
1 3 ! [ θ a ∧ ρ 0 T 0 ] [ θ a ∧ ρ 0 T 0 ] [ θ a ∧ ρ 0 T 0 ] = 1 3 ! [ ( θ a ∧ ) 3 ( θ a ∧ ) 2 ρ 0 T 0 ] \frac{1}{3!}\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]=\frac{1}{3!}\left[\begin{array}{c} (\theta\boldsymbol{a}^{\wedge})^3 & (\theta\boldsymbol{a}^{\wedge})^2\rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right] 3!1[θa∧0Tρ0][θa∧0Tρ0][θa∧0Tρ0]=3!1[(θa∧)30T(θa∧)2ρ0]
以此类推
1 n ! [ θ a ∧ ρ 0 T 0 ] n = 1 n ! [ ( θ a ∧ ) n ( θ a ∧ ) n − 1 ρ 0 T 0 ] (4-2-3) \frac{1}{n!}\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]^n=\frac{1}{n!}\left[\begin{array}{c} (\theta\boldsymbol{a}^{\wedge})^n & (\theta\boldsymbol{a}^{\wedge})^{n-1}\rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right] \tag{4-2-3} n!1[θa∧0Tρ0]n=n!1[(θa∧)n0T(θa∧)n−1ρ0](4-2-3)
那么,式(4-1-8)可化为
exp ( ξ ∧ ) = 1 n ! ∑ n = 0 ∞ [ ϕ ∧ ρ 0 T 0 ] n = I + [ θ a ∧ ρ 0 T 0 ] + [ ( θ a ∧ ) 2 θ a ∧ ρ 0 T 0 ] + . . . + 1 n ! [ ( θ a ∧ ) n ( θ a ∧ ) n − 1 ρ 0 T 0 ] = [ ∑ n = 0 ∞ 1 n ! ( θ a ∧ ) n ∑ n = 0 ∞ 1 ( n + 1 ) ! ( θ a ∧ ) n ρ 0 T 1 ] (4-2-4) \begin{aligned} \exp(\boldsymbol{\xi}^{\wedge})&=\frac{1}{n!}\sum_{n=0}^{\infty}\left[\begin{array}{c} \phi^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]^n \\ &=\boldsymbol{I}+\left[\begin{array}{c} \theta\boldsymbol{a}^{\wedge} & \rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]+\left[\begin{array}{c} (\theta\boldsymbol{a}^{\wedge})^2 & \theta\boldsymbol{a}^{\wedge}\rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]+...+\frac{1}{n!}\left[\begin{array}{c} (\theta\boldsymbol{a}^{\wedge})^n & (\theta\boldsymbol{a}^{\wedge})^{n-1}\rho \\ \boldsymbol{0}^{\mathrm{T}} & 0 \end{array}\right]\\ &=\left[\begin{array}{c} \sum_{n=0}^{\infty}\frac{1}{n!}(\theta\boldsymbol{a}^{\wedge})^n & \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\theta\boldsymbol{a}^{\wedge})^n\rho \\ \boldsymbol{0}^{\mathrm{T}} & 1 \end{array}\right] \tag{4-2-4} \end{aligned} exp(ξ∧)=n!1n=0∑∞[ϕ∧0Tρ0]n=I+[θa∧0Tρ0]+[(θa∧)20Tθa∧ρ0]+...+n!1[(θa∧)n0T(θa∧)n−1ρ0]=[∑n=0∞n!1(θa∧)n0T∑n=0∞(n+1)!1(θa∧)nρ1](4-2-4)
其中,左上角为 S O ( 3 ) SO(3) SO(3) 指数映射,前面已经证明。令
J = ∑ n = 0 ∞ 1 ( n + 1 ) ! ( θ a ∧ ) n = I + 1 2 ! θ a ∧ + 1 3 ! ( θ a ∧ ) 2 + 1 4 ! ( θ a ∧ ) 3 + 1 5 ! ( θ a ∧ ) 4 = 1 θ ( 1 2 ! θ 2 − 1 4 ! θ 4 + . . . ) a ∧ + 1 θ ( 1 3 ! θ 3 − 1 5 ! θ 5 + . . . ) ( a ∧ ) 2 + I = 1 − cos θ θ a ∧ + θ − sin θ θ ( a ∧ ) 2 + I = 1 − cos θ θ a ∧ + ( 1 − sin θ θ ) ( a a T − I ) + I = 1 − cos θ θ a ∧ + ( 1 − sin θ θ ) a a T − I + sin θ θ I + I = sin θ θ I + ( 1 − sin θ θ ) a a T + 1 − cos θ θ a ∧ (4-2-5) \begin{aligned} \boldsymbol{J}&=\sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\theta\boldsymbol{a}^{\wedge})^n \\ &=\boldsymbol{I}+\frac{1}{2!}\theta\boldsymbol{a}^{\wedge}+\frac{1}{3!}(\theta\boldsymbol{a}^{\wedge})^2+\frac{1}{4!}(\theta\boldsymbol{a}^{\wedge})^3+\frac{1}{5!}(\theta\boldsymbol{a}^{\wedge})^4 \\ &=\frac{1}{\theta}(\frac{1}{2!}\theta^2-\frac{1}{4!}\theta^4+...)\boldsymbol{a}^{\wedge}+\frac{1}{\theta}(\frac{1}{3!}\theta^3-\frac{1}{5!}\theta^5+...)(\boldsymbol{a}^{\wedge})^2+\boldsymbol{I} \\ &=\frac{1-\cos\theta}{\theta}\boldsymbol{a}^{\wedge}+\frac{\theta-\sin\theta}{\theta}(\boldsymbol{a}^{\wedge})^2+\boldsymbol{I}\\ &=\frac{1-\cos\theta}{\theta}\boldsymbol{a}^{\wedge}+(1-\frac{\sin\theta}{\theta})(\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{I})+\boldsymbol{I}\\ &=\frac{1-\cos\theta}{\theta}\boldsymbol{a}^{\wedge}+(1-\frac{\sin\theta}{\theta})\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{I}+\frac{\sin\theta}{\theta}\boldsymbol{I}+\boldsymbol{I}\\ &=\frac{\sin\theta}{\theta}\boldsymbol{I}+(1-\frac{\sin\theta}{\theta})\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}+\frac{1-\cos\theta}{\theta}\boldsymbol{a}^{\wedge} \tag{4-2-5} \end{aligned} J=n=0∑∞(n+1)!1(θa∧)n=I+2!1θa∧+3!1(θa∧)2+4!1(θa∧)3+5!1(θa∧)4=θ1(2!1θ2−4!1θ4+...)a∧+θ1(3!1θ3−5!1θ5+...)(a∧)2+I=θ1−cosθa∧+θθ−sinθ(a∧)2+I=θ1−cosθa∧+(1−θsinθ)(aaT−I)+I=θ1−cosθa∧+(1−θsinθ)aaT−I+θsinθI+I=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧(4-2-5)
注意,这里用到式(4-1-5) ( a ∧ ) 3 = − a ∧ (\boldsymbol{a}^{\wedge})^3=-\boldsymbol{a}^{\wedge} (a∧)3=−a∧ 和 a a T − I = a ∧ a ∧ \boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{I}=\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge} aaT−I=a∧a∧ 以及泰勒展开
cos θ = 1 − 1 2 ! θ 2 + 1 4 ! θ 4 + . . . \cos\theta=1-\frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4+... cosθ=1−2!1θ2+4!1θ4+...
sin θ = θ − 1 3 ! θ 3 + 1 5 ! θ 5 + . . . \sin\theta=\theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+... sinθ=θ−3!1θ3+5!1θ5+...
综上,证毕。
CH4-3 李代数求导
一、(1) S O ( 3 ) \mathrm{SO(3)} SO(3) 直接求导
对极几何:本质矩阵奇异值分解
矩阵内积和迹
矩阵具有 弗罗比尼乌斯内积,类似向量的内积。它被定义为两个相同大小的矩阵 A \boldsymbol{A} A 和 B \boldsymbol{B} B 的对应元素的积的和, 即
< A , B > = ∑ i = 1 n ∑ j = 1 n a i j b i j <\boldsymbol{A},\boldsymbol{B}>=\sum_{i=1}^{n}\sum_{j=1}^na_{ij}b_{ij} <A,B>=i=1∑nj=1∑naijbij
以 3 × 3 3\times 3 3×3 矩阵为例,设
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] , B = [ b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33 ] \boldsymbol{A}=\left[\begin{array}{c} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right], \boldsymbol{B}=\left[\begin{array}{c} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{array}\right] A= a11a21a31a12a22a32a13a23a33 ,B= b11b21b31b12b22b32b13b23b33
则有
< A , B > = ∑ i = 1 n ∑ j = 1 n a i j b i j <\boldsymbol{A},\boldsymbol{B}>=\sum_{i=1}^{n}\sum_{j=1}^na_{ij}b_{ij} <A,B>=i=1∑nj=1∑naijbij
对于 A T B \boldsymbol{A}^{\mathrm{T}}\boldsymbol{B} ATB
A T B = [ a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 ] [ b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33 ] = [ a 11 b 11 + a 21 b 21 + a 31 b 31 ? ? ? a 12 b 12 + a 22 b 22 + a 32 b 32 ? ? ? a 13 b 13 + a 23 b 23 + a 33 b 33 ] \boldsymbol{A}^{\mathrm{T}}\boldsymbol{B}=\left[\begin{array}{c} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{array}\right] \left[\begin{array}{c} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{array}\right]= \left[\begin{array}{c} a_{11}b_{11}+a_{21}b_{21}+a_{31}b_{31} & ? & ? \\ ? & a_{12}b_{12}+a_{22}b_{22}+a_{32}b_{32} & ? \\ ? & ? & a_{13}b_{13}+a_{23}b_{23}+a_{33}b_{33} \end{array}\right] ATB= a11a12a13a21a22a23a31a32a33 b11b21b31b12b22b32b13b23b33 = a11b11+a21b21+a31b31???a12b12+a22b22+a32b32???a13b13+a23b23+a33b33
则 T r ( A T B ) \mathrm{Tr}(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{B}) Tr(ATB)等于
T r ( A T B ) = a 11 b 11 + a 21 b 21 + a 31 b 31 + a 12 b 12 + a 22 b 22 + a 32 b 32 + a 13 b 13 + a 23 b 23 + a 33 b 33 = ∑ i = 1 n ∑ j = 1 n a i j b i j \mathrm{Tr}(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{B})=a_{11}b_{11}+a_{21}b_{21}+a_{31}b_{31}+a_{12}b_{12}+a_{22}b_{22}+a_{32}b_{32}+a_{13}b_{13}+a_{23}b_{23}+a_{33}b_{33}=\sum_{i=1}^{n}\sum_{j=1}^na_{ij}b_{ij} Tr(ATB)=a11b11+a21b21+a31b31+a12b12+a22b22+a32b32+a13b13+a23b23+a33b33=i=1∑nj=1∑naijbij
也就是说 A T B \boldsymbol{A}^{\mathrm{T}}\boldsymbol{B} ATB 的迹等于两矩阵对应元素相乘的积的和。
相关文章:
)
《视觉SLAM十四讲》公式推导(三)
文章目录 CH3-8 证明旋转后的四元数虚部为零,实部为罗德里格斯公式结果 CH4 李群与李代数CH4-1 SO(3) 上的指数映射CH4-2 SE(3) 上的指数映射CH4-3 李代数求导对极几何:本质矩阵奇异值分解矩阵内积和迹 CH3-8 证明旋转后的四元数虚部为零,实部…...

pnpm、npm、yarn的区别
pnpm、npm、yarn是三种不同的包管理器,它们之间有一些区别。 安装速度:pnpm的安装速度比npm和yarn快,因为它使用了只下载必需的模块,而不是下载整个依赖树。此外,pnpm还可以并行下载模块,从而进一步提高下…...
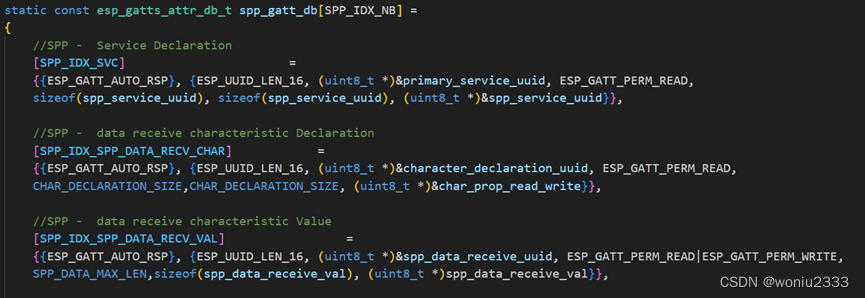
搞定蓝牙——第四章(GATT协议)
搞定蓝牙——第四章(GATT协议) 原理介绍层次结构server和client端Attribute ESP32代码 文章下面用的英文表示: server和client:服务端和客户端 char.:characteristic缩写,特征 Attribute:属性 ATT:Attribut…...

Go语言入门心法(十四): Go操作Redis实战
Go语言入门心法(一): 基础语法 Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 Go语言入门心法(四): 异常体系 Go语言入门心法(五): 函数 Go语言入门心法(六): HTTP面向客户端|服务端编程 Go语言入门心法(七): 并发与通道 Go语言入门心法(八): mysql驱动安装报错o…...
)
Java学习笔记(三)
前言 这个主要就是想记录一个点,就是二维数组保存的元素就是一维数组的地址,这个概念大家都知道了,那么接下来就是我最近写程序发生的一个事情了。 随机打乱一个一维数组 这个程序我相信大家都是会写的,通过randomArr来随机打乱…...

Flutter笔记:GetX模块中不使用 Get.put 怎么办
Flutter笔记 GetX模块中不使用 Get.put 怎么办 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/13400672…...

2023前端面试整理
1. 介绍一下最近参与的项目,负责那些业务,在开发过程中遇到过问题吗?最后是咋样处理的? 之前负责过大小十几个项目,负责过浙里办的整套上架流程,负责过数据大屏统计,后台管理系统文书生成表单生成等,浙政钉…...
文化融合:TikTok如何弥合跨文化差异
随着全球化的加速和数字媒体的崛起,社交媒体平台已经成为连接世界各地人们的纽带。其中,TikTok作为一个引领者,正在以惊人的速度消除跨文化差异,促进文化融合,使人们更加了解和尊重不同背景和传统。 本文将深入探讨Ti…...

asp.net core获取config和env
配置文件的读取和使用 //读取配置文件直接使用 var configModel configuration.GetSection("DataBaseConfig").Get<DataBaseConfigModel>(); //读取配置文件注入到IOC中 services.Configure<AssemblyConfig>(configuration.GetSection("AssemblyC…...

Git不常用命令(持续更新)
今日鸡汤:当你最满足的时候,通常也最孤独;当你最愤慨的时候,通常也最可怜。 此博文会列出一些平时不常用,但是能提高效率的git命令,后续会出IDEA对应的操作步骤 快看看你是不是都用过... 分支(…...

PostPreSql 数据库的一些用法
1、varchar 类型转换成数字 select sum(CAST(order_num AS NUMERIC)) from ads_port_cli_cons_freq_rpt where yr2023 and mon 08...
小工具推荐:FastGithub的下载及使用
前言:FastGithub是基于dotnet开发的一款开源Github加速器,通过自动获取与GitHub相关的IP地址并更新本地hosts文件来提高资源访问速度,使GitHub的访问畅通无阻。原理(复制过来的): ①修改本机的DNS服务指向…...

硬件信息查看工具 EtreCheckpro mac中文版功能介绍
etrecheckpro mac中文版是一款专业的硬件信息查看工具,它能够快速的检测Mac电脑的软硬件信息,加强用户对自己计算机的了解,EtreCheckPro for Mac下载首先会对电脑的软硬件信息进行扫描收集,之后才会显示出来。EtreCheck Mac版报告…...
宝塔Python3.7安装模块报错ModuleNotFoundError: No module named ‘Crypto‘解决办法
前言 今晚遇到一个问题,宝塔服务器上安装脚本的模块时,出现以下报错,这里找到了解决办法 Traceback (most recent call last):File "/www/wwwroot/unifysign/fuck_chaoxing/fuck_xxt.py", line 4, in <module>from Crypto.…...
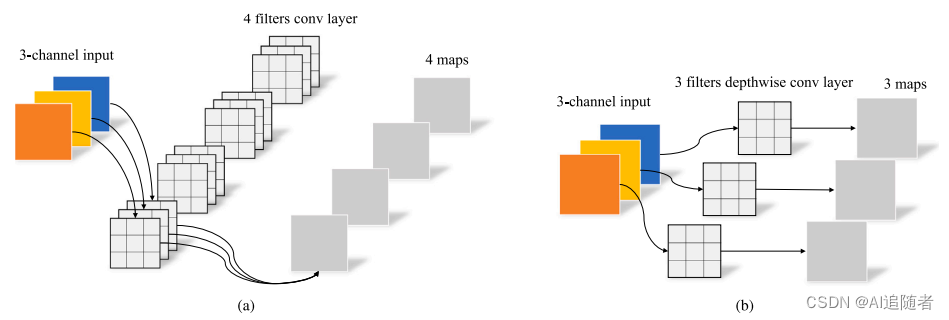
优化改进YOLOv5算法:加入ODConv+ConvNeXt提升小目标检测能力——(超详细)
为了提升无人机视角下目标检测效果,基于YOLOv5算法,在YOLOv5主干中实现了Omnidimensional Convolution(ODConv),以在不增加网络宽度和深度的情况下提高精度,还在YOLOv5骨干网中用ConvNeXt块替换了原始的C3块,以加快检测速度。 1 Omni-dimensional dynamic convolution …...

ElasticSearch安装、插件介绍及Kibana的安装与使用详解
ElasticSearch安装、插件介绍及Kibana的安装与使用详解 1.安装 ElasticSearch 1.1 安装 JDK 环境 因为 ElasticSearch 是用 Java 语言编写的,所以必须安装 JDK 的环境,并且是 JDK 1.8 以上,具体操作步骤自行百度 安装完成查看 java 版本 …...
JVM | 命令行诊断与调优 jhsdb jmap jstat jps
目录 jmap 查看堆使用情况 查看类列表,包含实例数、占用内存大小 生成jvm的堆转储快照dump文件 jstat 查看gc的信息,查看gc的次数,及时间 查看VM内存中三代(young/old/perm)对象的使用和占用大小 查看元数据空…...

SQL 表达式
SQL 表达式 表达式是计算值的一个或多个值、运算符和SQL函数的组合。这些SQL表达式类似于公式,它们是用查询语言编写的。 您还可以使用它们查询数据库中的特定数据集。 句法 考虑SELECT语句的基本语法,如下所示: SELECT column1, column2, …...
Unity3D 打包发布时生成文件到打包目录
有时候需要自己创建批处理文件或日志文件,在启动程序的同级目录使用,减少手动操作的时间和错误率。主要使用到的是OnPostprocessBuild方法。 1、在工程中的Editor文件夹下创建脚本 2、将文件放入Plugins的相关目录 3.脚本内容 using System.Collection…...

Elasticsearch中使用join来进行父子关联
在使用关系数据库进行开发的过程中,你可能会经常使用外键来表示父表和子表之间的关联关系,在Elasticsearch中,有哪些方法可以用来让开发者解决索引之间一对多和多对多的关联关系的问题呢 1 使用对象数组存在的问题 你可以很方便地把一个对象…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
