包子凑数(完全背包)
小明几乎每天早晨都会在一家包子铺吃早餐。
他发现这家包子铺有 N 种蒸笼,其中第 i种蒸笼恰好能放 Ai 个包子。
每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有 X 个包子。
比如一共有 33 种蒸笼,分别能放 3、4和 5 个包子。
当顾客想买 11 个包子时,大叔就会选 2 笼 3 个的再加 1 笼 5 个的(也可能选出 1笼 3 个的再加 2 笼 4 个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。
比如一共有 3 种蒸笼,分别能放 4、5 和 6 个包子。
而顾客想买 7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入格式
第一行包含一个整数 N。
接下来 N 行,每行包含一个整数 Ai。
输出格式
输出一个整数代表答案。
如果凑不出的数目有无限多个,输出INF。
数据范围
1≤N≤100
1≤Ai≤100输入样例1:
2 4 5输出样例1:
6输入样例2:
2 4 6输出样例2:
INF样例解释
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
#include <iostream>using namespace std;
constexpr int N=10010;
typedef long long ll;
int n;
bool dp[110][N];
int a[110],d;
int gcd(int x,int y){return y ? gcd(y,x%y) : x;
}
int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);d=gcd(d,a[i]);}if(d!=1) printf("INF\n");else {dp[0][0]= true;for(int i=1;i<=n;i++){for(int j=0;j<N;j++){dp[i][j]=dp[i-1][j];if(j>=a[i]){dp[i][j] |=dp[i][j-a[i]];}}}int res=0;for(int i=0;i<N;i++){if(!dp[n][i]){res++;}}printf("%d\n",res);}return 0;
}
相关文章:
)
包子凑数(完全背包)
小明几乎每天早晨都会在一家包子铺吃早餐。 他发现这家包子铺有 N 种蒸笼,其中第 i种蒸笼恰好能放 Ai 个包子。 每种蒸笼都有非常多笼,可以认为是无限笼。 每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若…...

Spring超级全家桶,学完绝对是惊艳面试官的程度
前言Spring框架自2002年诞生以来一直备受开发者青睐,它包括SpringMVC、SpringBoot、Spring Cloud、Spring Cloud Dataflow等解决方案。有人亲切的称之为:Spring 全家桶。很多研发人员把spring看作心目中最好的java项目,没有之一。所以这是重点…...

Redis主要数据类型
Redis 是一个数据结构服务器。 Redis 的核心是提供一系列本机数据类型,可帮助您解决从缓存到队列再到事件处理的各种问题Redis主要数据类型:String(字符串),Lists(列表),Sets&#x…...

【Linux | ELK 8.2】搭建ELKB集群Ⅰ—— 实验环境说明和搭建Elasticsearch集群
目录1. 实验环境1.1 实验工具1.2 操作系统1.3 架构版本、IP地址规划与虚拟机配置要求1.4 拓扑图1.5 其他要求2. 实验步骤2.1 安装Elasticsearch(单节点)(1)检查系统jdk版本(2)下载elasticsearch(…...
)
不同情况下*p和*p的区别(指针)
一说到指针,不少同学就会觉得云里雾里。首先要明白,指针和地址是一个概念;然后明白指针和指针变量的区别。先理解地址和数据,想象内存里面是一个个的小盒子,每个盒子对应一个编号,这个编号就是地址…...
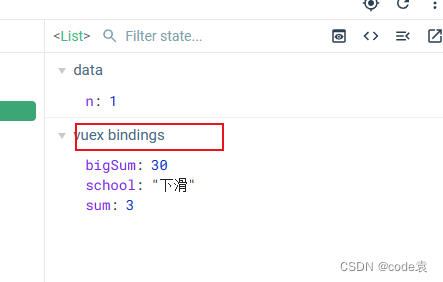
Vuex基础语法
Vuex vuex官网 文章目录Vuexvuex的工作原理图2.vuex的环境搭建3.vuex的使用1.actons2. mutations3.getters4.vuex中的map映射属性4.1 mapState和mapGetters4.2 mapMutations和mapActions5.vuex多组件通信1.通过计算属性获得2.通过mapState获得6.vuex模块化和命名空间6.1模块化…...
刚上岸字节测试开发岗,全网最真实的大厂面试真题
首先我来解释一下为什么说是全网最真实的面试题,相信大家也发现软件测试面试题在网上流传也已不少,但是经过仔细查看发现了两个很重要的问题。 第一,网上流传的面试题的答案并不能保证百分百正确。也就是说各位朋友辛辛苦苦花了很多时间准备…...

Mac监控键盘输入并执行动作
最新内容在我的另一个博客:Mac监控键盘输入并执行动作 背景 电脑的安全是非常重要的,特别是里面的敏感数据,若是被有心之人利用,那后果不堪设想。 所以我们部门定下了一个规矩,谁离开工位要是不锁屏,就可以…...

Transformer输出张量的值全部相同?!
Transformer输出张量的值全部相同?!现象原因解决现象 输入经过TransformerEncoderLayer之后,基本所有输出都相同了。 核心代码如下, from torch.nn import TransformerEncoderLayer self.trans TransformerEncoderLayer(d_mode…...

港科夜闻|全国政协副主席梁振英先生率香港媒体高管团到访香港科大(广州)...
关注并星标每周阅读港科夜闻建立新视野 开启新思维1、全国政协副主席梁振英先生率香港媒体高管团到访香港科大(广州)。2月21日下午,在全国政协副主席、广州南沙粤港合作咨询委员会顾问梁振英先生的带领下,香港20余家媒体的高管及知名媒体人士到访香港科大…...

XML调用 CAPL Test Function
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...
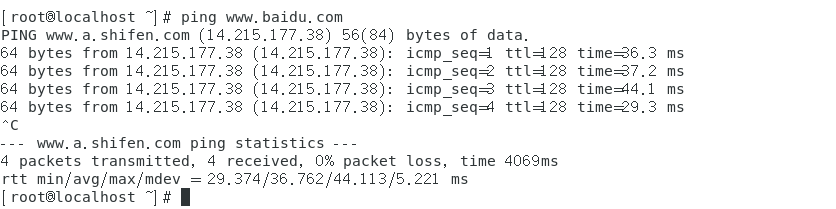
Linux网络配置(NAT)
在搭配好一台虚拟机的时候想要下载,安装些什么但一直失败这个时候就可以检查一下网络是否连接这里我们使用centos7举例子使用命令——ifconfig由此可见我们的系统中目前有3个网卡ens33——用于接入外网,该网卡默认关闭lo——用于访问本地网络,…...
——线性表总结)
数据结构——第二章 线性表(8)——线性表总结
线性表总结 线性表是线性结构的基本形式,用于描述一组同类型而具有1:1线性关系的数据对象。将此类数据对象存放在计算机的内存中时,必须考虑数据元素的存放和数据元素之间关系的存放。常用的存储结构有顺序存结构和链式结构。 顺序表存储特点是用一维数…...

3.7寸按键翻页工牌
产品参数 产品型号 ESL_BWR3.7_BLE 产品尺寸 (mm) 62.51066.5 显示技术 E ink 显示区域 (mm) 47.32(H)81.12(V) 分辨率 (像素) 280480 像素尺寸(mm) 0.1690.169 150dpi 显示颜色 黑/白 视觉角度 180 工作温度 0℃ - 50℃ 电池 500mAh ( Type-C 充电…...

西北工业大学大学物理(II)选填解析2019-2020期末
2 又是考查“一个电子和一个光子具有相同的波长,则二者动量相等。”4 斯特恩盖拉赫实验,原子的自旋磁矩取向量子化。7 通常我们感受不到电子的波动性。因为其波长短,其实也就是粒子运动速率高。10 考查无限长直导线周围B分布。常见的模型要记…...
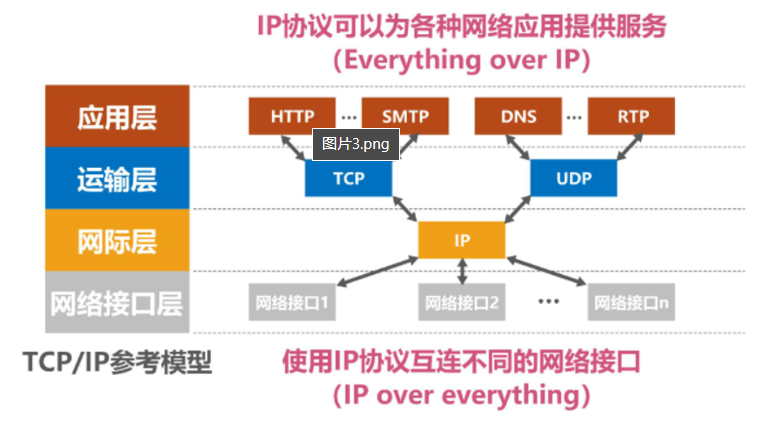
[计算机网络(第八版)]第一章 概述(章节测试/章节作业)
随堂作业 练习版(无答案版) 1.2 因特网概述 1【单选题】因特网的前身是1969年创建的第一个分组交换网 A、internetB、InternetC、NSFNETD、ARPANET 2【单选题】因特网采用的核心技术是 A、TCP/IPB、局域网技术C、远程通信技术D、光纤技术 1.3 三种交换方式:电路…...

华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典
文章目录2023 年用 Python 语言解华为 OD 机试题,一篇博客找全。华为 OD 机试题清单(机试题库还在逐日更新)2023 年用 Python 语言解华为 OD 机试题,一篇博客找全。 在 2023 年,Python 已成为广泛使用的编程语言之一&…...
电子科技大学数据库与软件工程三
适用于网工和物联网专业 目录 一、实验目的 二、实验内容 三、实验软件 四、实验步骤及数据记录 1.子查询 2. 伪列 3.数据库对象 4. 块、存储过程和触发器 五、实验结论及思考题 实验结论: 思考题: 六、总结及心得体会 七、对本实验过程及方…...

华为开源自研AI框架昇思MindSpore数据变换:Transforms
目录一、环境准备1.进入ModelArts官网2.使用CodeLab体验Notebook实例二、数据变换 TransformsCommon TransformsComposeVision TransformsRescaleNormalizeHWC2CWHText TransformsBasicTokenizerLookupLambda Transforms通常情况下,直接加载的原始数据并不能直接送入…...

软件测试之边界值测试法
边界值测试法 1. 介绍 边界值分析法就是对输入或输出边界值进行测试的,也是一种黑盒测试. 边界值分析法通常作为等价类划分法的补充,其测试用例来自等价类的边界;长期的经验得知,大量的错误是发现在输入或输出范围的边界上,而不是发生再输入输出范围的内部&#…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
