DAY35 435. 无重叠区间 + 763.划分字母区间 + 56. 合并区间
435. 无重叠区间
题目要求:给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
- 输入: [ [1,2], [2,3], [3,4], [1,3] ]
- 输出: 1
- 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
- 输入: [ [1,2], [1,2], [1,2] ]
- 输出: 2
- 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
- 输入: [ [1,2], [2,3] ]
- 输出: 0
- 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
思路
按照右边界排序,从左向右记录非交叉区间的个数。最后用总区间数减去非交叉区间的个数就是需要移除的区间的个数。
核心:把所有规则下有重叠的区间当作是一个区间来考虑。
class Solution {
public:static bool cmp(const vector<int>& a, const vector<int>& b) {return a[1] < b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.size() == 0) return 0;sort(intervals.begin(), intervals.end(), cmp);int count = 1;int end = intervals[0][1];for (int i = 1; i < intervals.size(); ++i) {if (end <= intervals[i][0]) {end = intervals[i][1];count++;}}return intervals.size() - count;}
};763.划分字母区间
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
示例:
- 输入:S = "ababcbacadefegdehijhklij"
- 输出:[9,7,8] 解释: 划分结果为 "ababcbaca", "defegde", "hijhklij"。 每个字母最多出现在一个片段中。 像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
提示:
- S的长度在[1, 500]之间。
- S只包含小写字母 'a' 到 'z' 。
思路
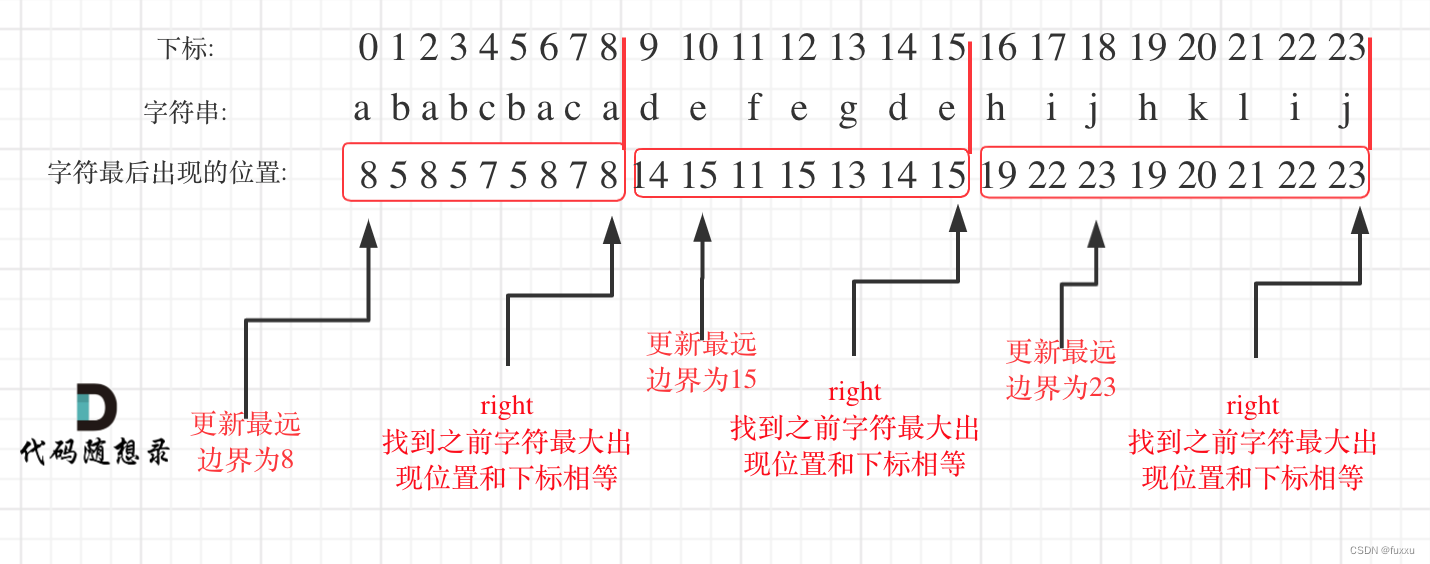
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
class Solution {
public:vector<int> partitionLabels(string s) {int hash[27] = {0};for (int i = 0; i < s.size(); ++i) {hash[s[i] - 'a'] = i; // 更新每个字符出现的最后位置}vector<int> result;int left = 0;int right = 0;for (int i = 0; i < s.size(); ++i) {right = max(right, hash[s[i] - 'a']); // 找到字符出现的最远边界if (i == right) {result.push_back(right - left + 1);left = i + 1;}}return result;}
};56. 合并区间
题目要求:给出一个区间的集合,请合并所有重叠的区间。
示例 1:
- 输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
- 输出: [[1,6],[8,10],[15,18]]
- 解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
- 输入: intervals = [[1,4],[4,5]]
- 输出: [[1,5]]
- 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
思路
首先需要先按照左边界排序。先判断重叠,然后不断更新重叠的左右边界,当遇到不重叠时计入res数组。
按照左边界排序可以保证最小的左边界在前,可以直接把第一个左边界push进结果数组,在更新时也只需要对重叠进行判断而不需要判断左边界的关系。
class Solution {
public:static bool cmp(const vector<int>& a, const vector<int>& b) {return a[0] < b[0];}vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> result;if (intervals.size() == 0) return result;sort(intervals.begin(), intervals.end(), cmp);result.push_back(intervals[0]);for (int i = 1; i < intervals.size(); ++i) {if (result.back()[1] >= intervals[i][0]) {result.back()[1] = max(result.back()[1], intervals[i][1]);} else {result.push_back(intervals[i]);}}return result;}
};- 时间复杂度: O(nlogn)
- 空间复杂度: O(logn),排序需要的空间开销
/ec = 该C++代码片段是用于合并区间的。主要有以下几个部分需要考虑时间复杂度:
1. `sort(intervals.begin(), intervals.end(), cmp);`:这一行代码的时间复杂度是O(n log n),其中n是区间的数量。这里使用了标准库的排序算法。
2. 循环 `for (int i = 1; i < intervals.size(); ++i)`:这一行代码开始的循环有O(n)的时间复杂度。在循环内部,所有操作(包括vector的push_back和max函数)都是O(1)的时间复杂度。
因此,总体时间复杂度是O(n log n) + O(n) = O(n log n)。
所以,这个代码的时间复杂度是O(n log n)。
相关文章:

DAY35 435. 无重叠区间 + 763.划分字母区间 + 56. 合并区间
435. 无重叠区间 题目要求:给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。 注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。 示例 1: 输入: [ […...
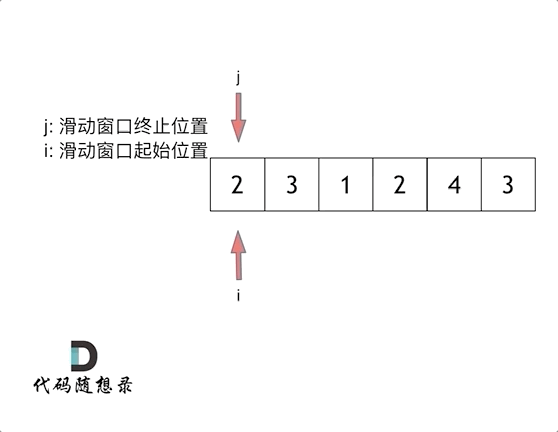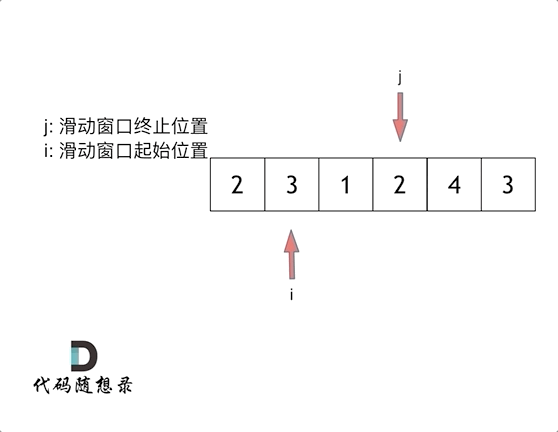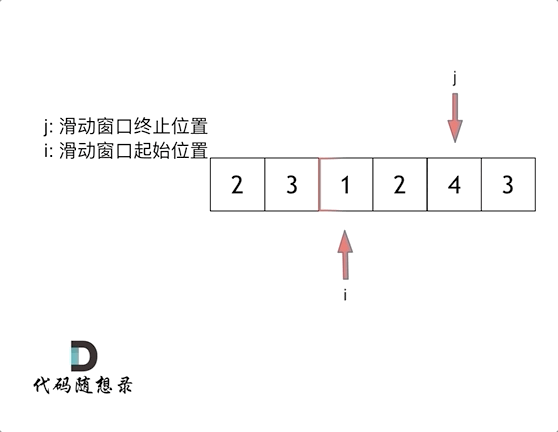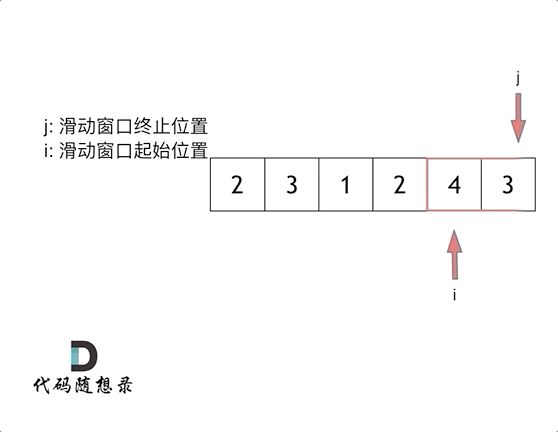
代码随想录算法训练营第2天| 977有序数组的平方、209长度最小的子数组。
JAVA代码编写 977. 有序数组的平方 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释&…...

微信小程序通过startLocationUpdate,onLocationChange获取当前地理位置信息,配合腾讯地图解析获取到地址
先创建个getLocation.js文件 //获取用户当前所在的位置 const getLocation () > {return new Promise((resolve, reject) > {let _locationChangeFn (res) > {resolve(res) // 回传地里位置信息wx.offLocationChange(_locationChangeFn) // 关闭实时定位wx.stopLoc…...

C/C++字符三角形 2020年12月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C字符三角形 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C字符三角形 2020年12月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 给定一个字符,用它构造一个底边长5个字…...

Python数据挖掘:入门、进阶与实用案例分析——基于非侵入式负荷检测与分解的电力数据挖掘
文章目录 摘要01 案例背景02 分析目标03 分析过程04 数据准备05 属性构造06 模型训练07 性能度量08 推荐阅读赠书活动 摘要 本案例将根据已收集到的电力数据,深度挖掘各电力设备的电流、电压和功率等情况,分析各电力设备的实际用电量,进而为电…...
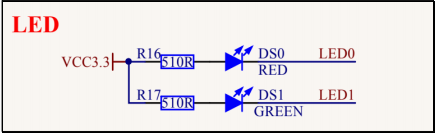
基于 Qt控制开发板 LED和C语言控制LED渐变亮度效果
## 资源简介 在STM32开发板,板载资源上有两个可自由控制的 LED。如下图原理 图其中我们以操作 LED1 为示例,LED1 为出厂系统的心跳指示灯。 ## 应用实例 想要控制这个 LED,首先出厂内核已经默认将这个 LED 注册成了 gpio-leds类型设备。所以我们可以直接在应用层接口直接…...
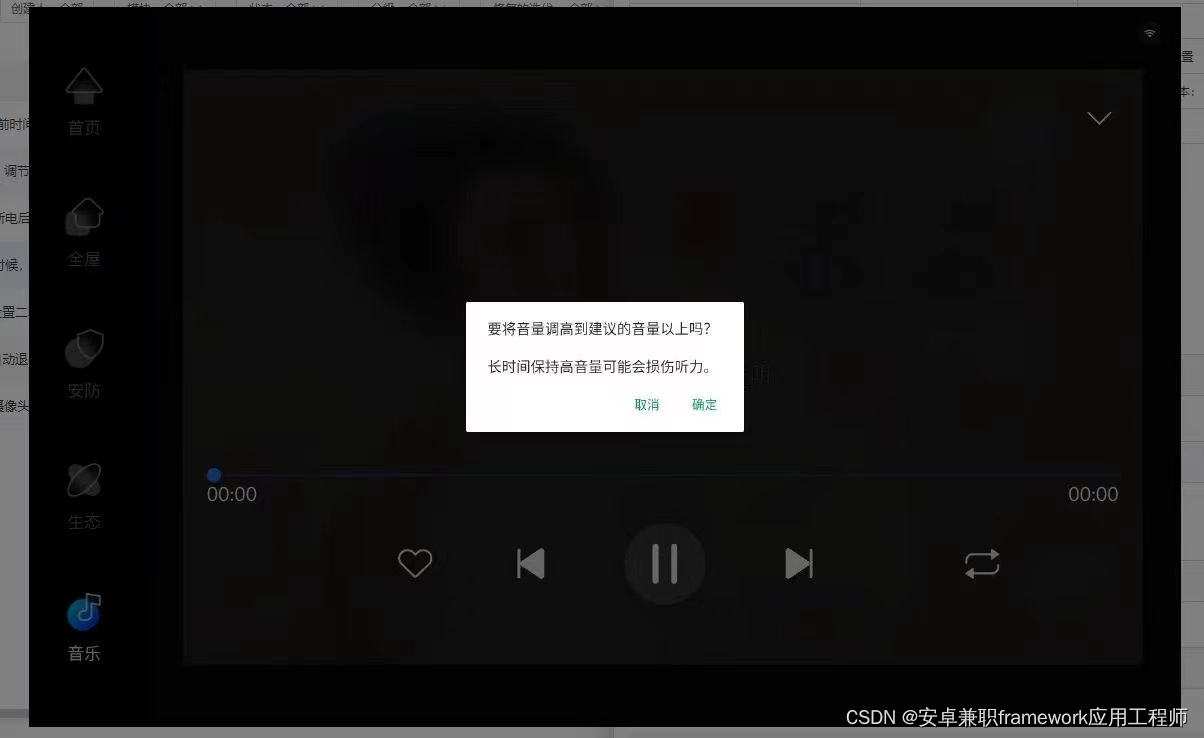
Android 11.0 禁用插入耳机时弹出的保护听力对话框
1.前言 在11.0的系统开发中,在某些产品中会对耳机音量调节过高限制,在调高到最大音量的70%的时候,会弹出音量过高弹出警告,所以产品 开发的需要要求去掉这个音量弹窗警告功能 2.禁用插入耳机时弹出的保护听力对话框的核心类 frameworks\base\packages\SystemUI\src\com\and…...
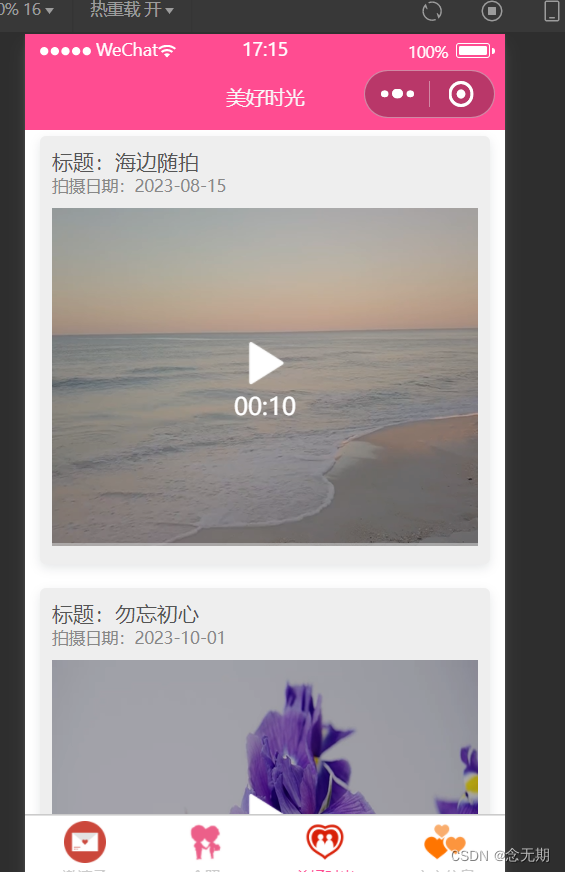
微信小程序案例2-3:婚礼邀请函
文章目录 一、运行效果二、知识储备(一)导航栏配置(二)标签栏配置(三)vw、vh单位(四)video组件(五)表单组件(六)Node.js概述 三、实现…...
K8S部署Dashboard
获取recommended.yaml文件 Dashboard是官方提供的一个UI,可用于基本管理K8s资源。 YAML下载地址: wget https://raw.githubusercontent.com/kubernetes/dashboard/v2.4.0/aio/deploy/recommended.yaml如果网络错误无法直接下载,可以直接访问…...

【OJ比赛日历】快周末了,不来一场比赛吗? #10.29-11.04 #7场
CompHub[1] 实时聚合多平台的数据类(Kaggle、天池…)和OJ类(Leetcode、牛客…)比赛。本账号会推送最新的比赛消息,欢迎关注! 以下信息仅供参考,以比赛官网为准 目录 2023-10-29(周日) #3场比赛2023-10-30…...

常用应用安装教程---在centos7系统上安装Docker
在centos7系统上安装Docker 1:切换镜像源 wget https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo -O /etc/yum.repos.d/docker-ce.repo2:查看当前镜像源中支持的docker版本 yum list docker-ce --showduplicates | sort -r3&#x…...
CTFHub-SSRF-读取伪协议
WEB攻防-SSRF服务端请求&Gopher伪协议&无回显利用&黑白盒挖掘&业务功能点-CSDN博客 伪协议有: file:/// — 访问本地文件系统 http:/// — 访问 HTTP(s) 网址 ftp:/// — 访问 FTP(s) URLs php:/// — 访问各个输入/输出流(I/O streams) dic…...

推荐一款适合科技行业的CRM系统
推荐您一款科技行业好用的CRM系统——Zoho CRM客户管理系统,旨在帮助企业管理客户数据、销售过程、营销活动以及服务支持,助力业务增长及数字化转型,实现“以客户为中心”的企业管理和运营模式。 近些年,随着政府鼓励政策的出台、…...
ChatGPT 与 Python Echarts 完成热力图实例
热力图是一种数据可视化方式,它通过颜色的变化来表示数据的差异和分布。以下是使用热力图的一些作用和好处: 数据可视化:热力图可以将复杂的数据集转化为更直观、更易理解的形式。这对于很多人来说,尤其是那些没有深入统计学或数…...

vue3项目报错The template root requires exactly one element.eslint-plugin-vue
解决方案: 1.禁用 Vetur 并改用Volar》它现在是 Vue 3 项目的官方推荐。【必须重启vsCode】 从官方迁移指南: 建议使用带有我们官方扩展 Volar (opens new window) 的 VSCode,它为 Vue 3 提供了全面的 IDE 支持。 2.package.json文件中 &…...
【C++系列】STL容器——vector类的例题应用(12)
前言 大家好吖,欢迎来到 YY 滴C系列 ,热烈欢迎!本章主要内容面向接触过C的老铁,下面是收纳的一些例题与解析~ 主要内容含: 目录 【例1] 只出现一次的数字i(范围for与模等(^))【例2]…...

常用应用安装教程---在centos7系统上安装JDK8
在centos7系统上安装JDK8 1:进入oracle官网下载jdk8的tar.gz包: 2:将下载好的包上传到每个服务器上: 3:查看是否上传成功: [rootkafka01 ~]# ls anaconda-ks.cfg jdk-8u333-linux-x64.tar.gz4…...

阿里云/腾讯云国际站代理:国际腾讯云的优势
国际腾讯云具有以下优势: 1. 全球覆盖:腾讯云在全球拥有30个区域,覆盖6个大洲,能够提供全球范围的云服务,满足不同地区用户的需求。 2. 大规模网络:腾讯云拥有庞大的全球网络,包括多个高速骨干…...

【软件教程】如何用C++检查TCP或UDP端口是否被占用
一、检查步骤 使用socket函数创建socket_fd套接字。使用sockaddr_in结构体配置协议和端口号。使用bind函数尝试与端口进行绑定,成功返回0表示未被占用,失败返回-1表示已被占用。 二、CODE 其中port需要修改为想要检测的端口号,也可以将代码…...

Flutter报错RenderBox was not laid out: RenderRepaintBoundary的解决方法
文章目录 报错问题分析问题原因 解决办法RenderBox was not laid out错误的常见原因常见原因解决方法 RenderRepaintBoundaryRenderRepaintBoundary用途 报错 RenderBox was not laid out: RenderRepaintBoundary#d4abf relayoutBoundaryup1 NEEDS-PAINT NEEDS-COMPOSITING-BI…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
