二叉排序树
二叉排序树定义及性质
二叉排序树(Binary Sort Tre)或者是一棵空树,或者是具有如下性质的二叉树:
(1) 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2) 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3) 它的左右子树也分别为二叉排序树。
简单来说,二叉排序树是指根结点大于左子树,小于右子树的二叉树。
根据使用目的,二叉排序树也常被称为二叉查找树、二叉搜索树。
二叉排序树的存储结构
二叉排序树存储结构与二叉树的存储结构一致,常见的存储方式有两种:顺序存储结构、链式存储结构。在实际开发中,链式存储结构是使用最多的。这里重点介绍下链式存储结构。
链式存储结构
不同的存储结构可构成不同形式的链式存储结构。二叉排序树的链式存储结构与二叉树的链式存储结构一致。由二叉树的定义可知,二叉树的结点由一个数据元素和分别指向左右子树的两个分支构成。有时,为了便于查找结点的双亲,还会增加一个指向其双亲结点的指针域。对应存储形式如下图所示:
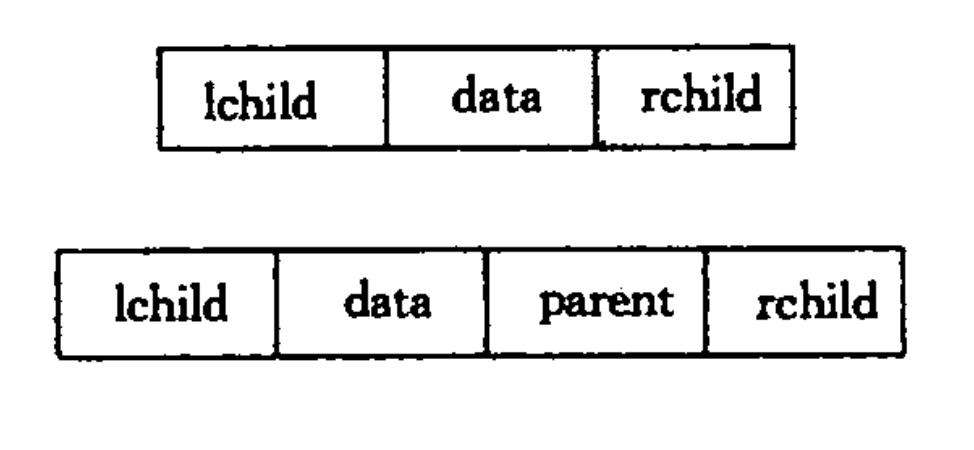
二叉排序树的操作
同一种操作,不同的存储结构,对应不同的实现。本文仅介绍基于链式存储结构的实现。同时,这里仅介绍基本的操作,更多高级的操作可以参考力扣。
二叉排序树的查找
二叉排序树中关键字的查找过程如下:当二叉排序树不空时,首先将给定值的和根结点的关键字比较,若相等,则查找成功,否则将依据给定值和根结点的关键字之间的大小关系,分别在左子树或右子树上继续进行查找。对于二叉链表为存储结构的二叉树来说,其查找算法如下所示:
BiTree SearchBST(BiTree T, KeyType key) {// 在根指针 T 所指二叉排序树中递归地查找某关键字等于key的数据元素,// 若查找成功,则返回指向该数据元素结点的指针,否则返回空指针if((!T) || EQ(key, T->data.key)) {return (T); // 查找结束} else if(LT(key, T->data.key)) {return SearchBST(T->lchild, key); // 在左子树中继续查找} else {return SearchBST(T->rchild, key); // 在右子树中继续查找}
}
接下来考虑该算法的执行效率。含有 n n n个结点的二叉排序树的平均查找长度和树的形态有关。当先后插入的关键字有序时,构成的二叉排序树蜕变成单支树。树的深度为 n n n,其平均查找长度为 ( n + 1 ) / 2 (n+1)/2 (n+1)/2(和顺序查找相同),这是最差的情况。最好的情况则是二叉排序树的形态和折半查找的判定树相同,其平均查找长度和 l o g 2 n log_2 n log2n成正比。接下来分析二叉排序树的平均查找性能。
假设二叉排序树中 n n n个关键字的排列是"随机"的,即任一关键字在序列中将是第1个,或第2个,…,或第 n n n个的概率是相同的,那么平均查找长度 P ( n ) P(n) P(n)可以表示为:
P ( n ) = 1 n ∑ i = 0 n − 1 P ( n , i ) P(n) = \frac{1}{n}\sum_{i=0}^{n-1}P(n, i) P(n)=n1i=0∑n−1P(n,i)
显然, P ( n ) = 0 P(n) = 0 P(n)=0, P ( 1 ) = 1 P(1) = 1 P(1)=1。对于上述公式,当 n > = 2 n>=2 n>=2时,可表示为:
P ( n ) < = 2 ( 1 + 1 n ) l n n P(n) <= 2(1+\frac{1}{n})ln n P(n)<=2(1+n1)lnn
具体化简过程,可参考《数据结构》的9.2.1 二叉排序树和平衡二叉树。
由此可见,在关键字排列随机的情况下,二叉排序树的平均查找长度和 l o g n log n logn是等数量级的。
这里给出基于java的二叉树查找实现:
public TreeNode searchBST(TreeNode root, int val) {if(root == null) {return null;}if(val == root.val) {return root;} else if(val < root.val) {return searchBST(root.left, val);} else {return searchBST(root.right, val);}
}
为了消减递归调用,这里使用循环的方式,给出实现方式。更多使用循环替代递归的通用知识可以参考通用的递归转循环方法一文。
public TreeNode searchBST(TreeNode root, int val) {while (root != null) {if(val == root.val) {break;} else if(val < root.val) {root = root.left;} else {root = root.right;}}return root;
}
更多二叉树查找的实现可以参考力扣。
二叉排序树的插入
一个无序序列可以通过构造一棵二叉排序树而变成一个有序序列,构造树的过程即为对无序序列进行排序的过程。而且每次向二叉排序树上插入新的结点都是二叉排序树上新的叶子节点,所以在进行插入操作时,不必移动其他结点,仅需改动某个结点的指针,由空变为非空即可。这就相当于在一个有序序列上插入一个记录而不需要移动其他记录。这表明二叉排序树既拥有类似折半查找的特性,又采用了链表作为存储结构,因此是动态查找表的一种合适表示。
二叉排序树中关键字的插入过程如下:首先根据给定值查找给定值是否已经存在二叉排序树中,如果存在,则直接返回。否则将结点插入到这棵树种。对于二叉链表为存储结构的二叉树来说,其插入算法如下所示:
Status SearchBST(BiTree T, keyType key, BiTree f, BiTree &p) {// 在根指针T所指二叉排序树中递归地查找器关键字等于key的数据元素,若查找成功,// 则指针p指向该数据元素节点,并返回TRUE,否则指针p指向查找路径上访问的最后一个结点// 并返回FALSE,指针f指向T的双亲,其初始调用值为 NULLif(!T) {p = f;return FALSE;} else if(EQ(key, T->data.key)) {p = T;return TRUE;} else if(LT(key, T->data.key)) {return SearchBST(T->lchild, key, T, p);} else {return SearchBST(T->rchild, key, T, p);}
}Status InsertBST(BiTree &T, ElemType e) { // 当二叉排序树T 中不存在关键字等于e.key的数据元素,插入e并返回TRUE,// 否则返回FALSEif(!SearchBST(T, e.key, NULL, p)) {s = (BiTree) malloc(sizeof(BiTNode));s->data = e;s->lchild = NULL;s->rchild = NULL;if(!p) {T = s;} else if(LT(e.key, p->data.key)) {p->lchild = s;} else {p->rchild = s; }} else {return FALSE;}
}
接下来考虑该算法的执行效率。分析其伪代码实现可知,插入数据依赖查找其待插入位置,所以每次插入的时间复杂度和查找的时间复杂度相同,也为 l o g n log n logn。
因为Java语言无法使用指针,这里给出基于Java语言的的二叉排序树插入实现时假定待插入数据一定不存在:
public TreeNode insertIntoBST(TreeNode root, int val) {if(root == null) {return new TreeNode(val);}if(root.val > val) {root.left = insertIntoBST(root.left, val);} else {root.right = insertIntoBST(root.right, val);}return root;
}
更多二叉树插入的实现可以参考力扣。
二叉排序树的删除
对于一般的二叉树来说,删除树中的一个结点是没有意义的。因为这将使被删除结点为根的子树成为森林,破坏了整棵树的结构。然而,对于二叉排序树来说,删去树上一个结点相当于删去有序序列中的一个记录,只要在删除某个结点之后依旧保持二叉排序树的性质即可。
那么,如何在二叉排序树上删去一个结点呢?假设在二叉排序树上被删除结点为*p(指向结点的指针为p),其双亲结点为*f(结点指针为f),且不失一般性,可设的左孩子。那么可以分以下三种情况进行讨论:
(1) 若*p结点为叶子节点,即 P L P_L PL和 P R P_R PR均为空树。由于删除叶子结点不破坏整棵树的结构,则只需修改其双亲结点的指针即可。
(2) 若*p结点只有左子树 P L P_L PL或者只有右子树 P R P_R PR,此时只要令 P L P_L PL或者 P R P_R PR直接成为其双亲结点*f的左子树即可。显然,作此修改也不破坏二叉排序树的性质。
(3) 若*p结点的左子树和右子树均不空,此时不能如上简单处理。在删去*p之后,为保持其他元素之间的相对位置不变,可以有两种做法:其一是令*p的左子树为*f的左子树,而*p的右子树为其直接前驱或直接后继的右子树。其二是令*p的直接前驱(或直接后继)替代*p,然后从二叉排序树中删去那个直接前驱(或直接后继)。
其删除算法如下所示:
Status DeleteBST(BiTree &T, KeyType key) {// 若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素节点,// 并返回TRUE,否则返回FALSEif(!T) { return FALSE;}if(EQ(key, T->data.key)) {return Delete(T);} else if(LT(key, T->data.key)) {return DeleteBST(T->lchild, key);} else {return DeleteBST(T->rchild, key);}
}Status Delete(BiTree &p) {// 从二叉排序树中删除结点p,并重接它的左子树或右子树if(!p->rchild) { // 右子树为空,则只需重接其左子树q = p;p = p->lchild;free(q);} else if(!p->lchild) { // 左子树为空,则只需重接其右子树q = p;p = p->rchild;free(q);} else { // 左子树和右子树均不为空q = p;s = p -> lchild;while(s->rchild) { // 转左,然后向右到尽头q = s;s = s->rchild;}p->data = s-> data; // s指向被删除结点的前驱if(q != p) { // 重接*q的右子树q->rchild = s->lchild;}else { // 重接*q的左子树q->lchild = s->lchild;}delete s;}return TRUE;
}
接下来考虑该算法的执行效率。分析其伪代码实现可知,删除数据前需要先查找到待删除结点,然后移动相关结点,所以每次删除的时间复杂度和查找的时间复杂度相同,也为 l o g n log n logn。
这里给出基于Java语言的的二叉排序树删除实现:
public TreeNode deleteNode(TreeNode root, int key) {if(root == null) {return null;}if(root.val == key) {root = delete(root);}else if(root.val > key) {root.left = deleteNode(root.left, key);} else {root.right = deleteNode(root.right, key);}return root;
}private TreeNode delete(TreeNode root) {if (root.left == null && root.right == null) {return null;}if (root.right == null) {return root.left;}if (root.left == null) {return root.right;}TreeNode successor = root.right;while (successor.left != null) {successor = successor.left;}root.right = deleteNode(root.right, successor.val);successor.right = root.right;successor.left = root.left;return successor;
}
更多二叉树删除的实现可以参考力扣。
参考
《数据结构》 严蔚敏 吴伟民 著 9.2.1 二叉排序树和平衡二叉树
https://blog.csdn.net/L_T_W_Y/article/details/108407686 数据结构——二叉搜索树详解
https://leetcode.cn/tag/binary-search-tree/problemset/ 二叉搜索树
https://leetcode.cn/problems/search-in-a-binary-search-tree/description/ 700. 二叉搜索树中的搜索
https://leetcode.cn/problems/insert-into-a-binary-search-tree/description/ 701. 二叉搜索树中的插入操作
https://leetcode.cn/problems/delete-node-in-a-bst/description/ 450. 删除二叉搜索树中的节点
https://blog.csdn.net/COCO56/article/details/96971844 markdown 数学公式 累加、连乘与乘号的代码
https://blog.csdn.net/qq_43444349/article/details/105400052 全面整理Typora的Latex数学公式语法
相关文章:

二叉排序树
二叉排序树定义及性质 二叉排序树(Binary Sort Tre)或者是一棵空树,或者是具有如下性质的二叉树: (1) 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; (2) 若它的右子树不空,则右子树上所有结点的值均…...
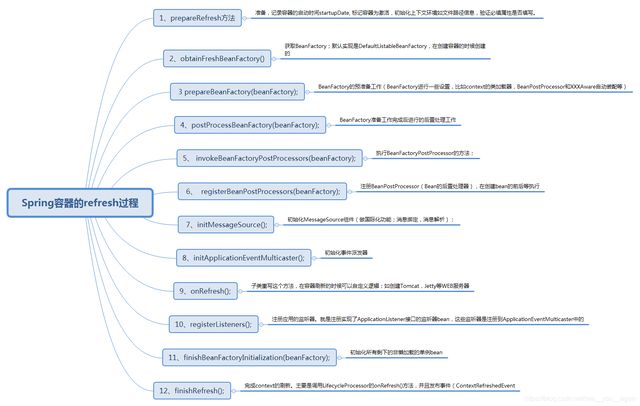
探秘Spring的设计精髓,深入解析架构原理
序员与平庸的程序员之间的区别,是在于认为自己的代码重要还是数据结构更加重要。平庸的程序员眼里只有代码,优秀的程序员则关注数据结构及之前的关系。” 1、spring的设计理念 spring提供了一个轻量级的开发框架,抽象了实际开发中的很多共…...

Python Wordcloud报错:Only supported for TrueType fonts,多种解决方案
Python Wordcloud报错:Only supported for TrueType fonts,多种解决方案。 报错内容如下: 2023-10-26T09:35:41.190459839Z Traceback (most recent call last): 2023-10-26T09:35:41.190502589Z File “lib/task/compute.py”, line 621, i…...

为虚拟网络提供敏捷负载均衡:Everoute LB 特性解读
为了保证应用系统的可用性,同时避免并发访问导致后端服务器出现性能瓶颈,不少用户都通过负载均衡技术优化流量分发。随着虚拟化平台下用户业务规模的持续扩大,虚拟化网络的数据访问量也不断增加,而传统负载均衡通常通过硬件负载均…...
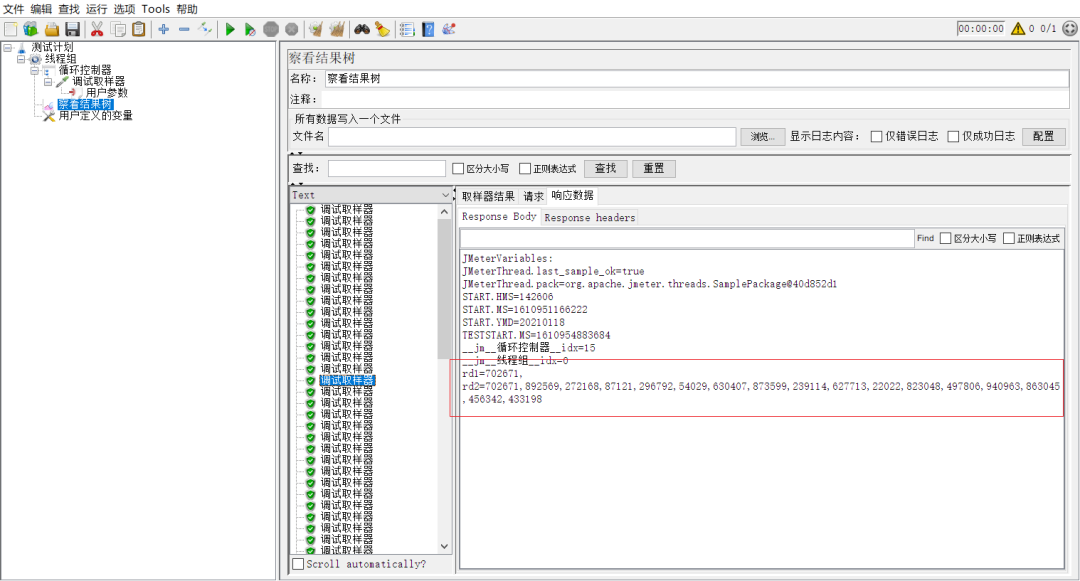
Jmeter 接口测试,参数值为列表,如何参数化?
最近在我的教学过程中,我的一个学生问了我一个问题,他们公司的一个接口参数值是列表,列表中值的数量有多有少,问我在 jmeter 中如何让这个参数的值进行参数化? 看到这种问题,你的第一反应是什么?…...

DeepinV20实现使用CapsLock键切换输入法
概览 起因参考资料解决问题1. 删除CapsLock键映射关系2. 新建CapsLock键映射关系3. 建立配置文件4. **注销用户或者重启电脑**5. 修改切换输入法快捷键6. 测试输入 起因 看同事的MacBook可以使用CapsLock键切换输入法,而我作为Shift党CapsLock键几乎不使用…...
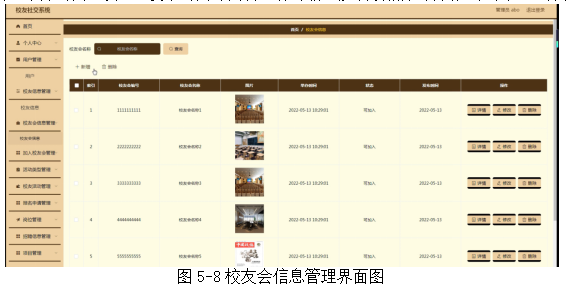
基于springboot实现校友社交平台管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现校友社交平台管理系统演示 摘要 校友社交系统提供给用户一个校友社交信息管理的网站,最新的校友社交信息让用户及时了解校友社交动向,完成校友社交的同时,还能通过论坛中心进行互动更方便。本系统采用了B/S体系的结构,使用了java技…...
WordPress主题模板 大前端D8 5.1版本完整开源版源码简洁大气多功能配置
源码测评:该模板官方已更新至5.2,但是这个5.1也是非常好用的,经测试所有页面均完好,推荐下载使用。 模板简介: 大前端D8 主题是一款非常牛逼的WordPress博客主题,响应式,功能齐全,支持手机,电脑,平板,非常适合做博客站…...

如何在Postman中使用静态HTTP
首先,打开 Postman 软件。在 Postman 的菜单栏中,点击 “Preferences”(偏好设置)。 亲身经验:我自己尝试了这个方法,发现它非常适用于需要使用HTTP的场景。 数据和引证:根据 Postman 官方文档…...

vscode 提升Vue开发效率的必备插件与工具
1,Vetur:提供了Vue语法高亮、智能提示、代码片段、错误检查和格式化等功能,是Vue开发中必不可少的插件。 2,ESLint:用于检查和修复JavaScript和Vue代码中的语法错误和潜在问题,提高代码质量。 3ÿ…...
mysql/java/springboot/javaweb请假系统,分为学生/辅导员/超级管理员
源码下载地址 支持:远程部署/安装/调试、讲解、二次开发/修改/定制 系统分为 学生/辅导员/超级管理员 学生 辅导员 超级管理员...

Android11系统桌面隐藏指定APP图标
做项目时有时会遇到这样的需求,客户要求隐藏Launcher3桌面的某个app图标,但是又不能删除去掉这个app,具体修改如下: diff --git a/src/com/android/launcher3/model/LoaderTask.java b/src/com/android/launcher3/model/LoaderTa…...
WEB使用百度地图展示某地地址
第一步 进入百度地图开发平台 百度地图开放平台 | 百度地图API SDK | 地图开发 第二步注册 获取AK秘钥,点击【创建应用】进入AK申请页面,填写应用名称,务必选择AK类型为“浏览器端”,JS API只支持浏览器端AK进行请求与访问 下面…...

22年上半年下午题
第一大题题目 第一大题解答 第一小问 看加工交互和说明来得出实体的名字。如果不太确定,可以多去看几条数据流来确认答案。仔细一点,这分稳啦。 第二小问 需要对应加工结合说明得出数据存储的名称。 一般可以在后面加上表字或者加上信息表。自拟&…...
)
大文件分片上传-续传-秒传(详解)
前言 前面记录过使用库实现的大文件的分片上传 基于WebUploader实现大文件分片上传 基于vue-simple-uploader 实现大文件分片上传 前面记录过基于库实现的大文件的分片上传,那如果不使用库, 文件分片是怎么实现的,该怎么做到呢?…...

CE-LVD证书跟CE-EMC证书有什么区别?
CE-LVD证书跟CE-EMC证书有什么区别? CE-LVD证书跟CE-EMC证书有什么区别? 近日,TEMU平台电器需提交CE-LVD证书,不再接受EMC证书---玩具产品需提交满足玩具法规的CE证书,法规总是多变的,卖家也是很苦恼&…...

使用Mapster实现双向映射,解放搬砖体力活
经常会有对象属性互相赋值的操作,但是频繁的写实在是搬运工一样,比较难受比如下面两个类 public class AgencyBdm {public new int Id { set; get; }public string AgencyId { set; get; }public string AgencyName { set; get; }public string Region {…...
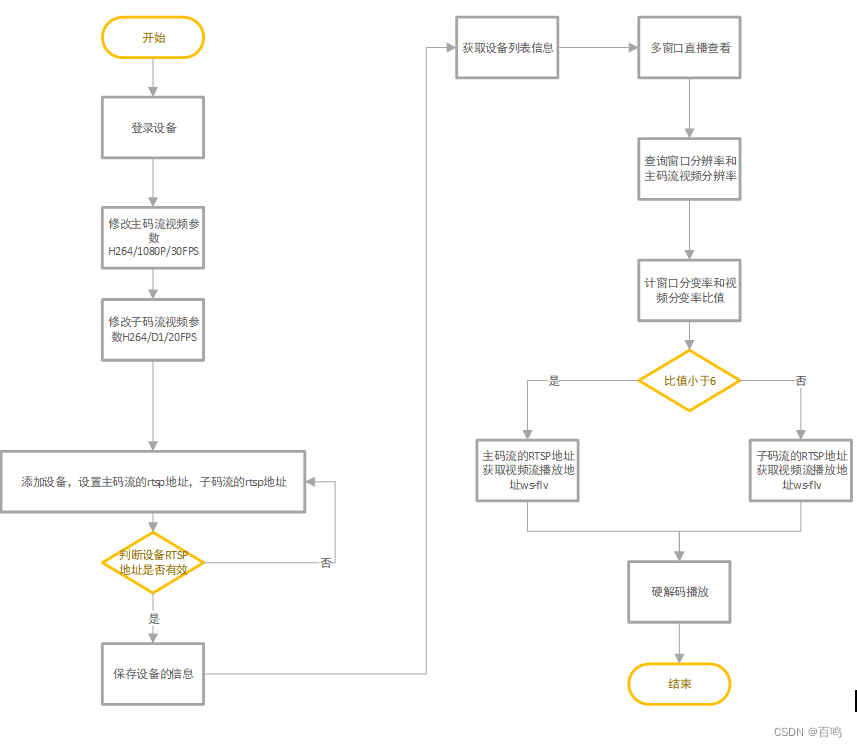
一种基于屏幕分辨率的RTSP主子码流切换的多路视频监控的播放方案
技术背景: 用户场景下,存在多个监控场所的100路监控摄像头,例如:大华、海康、宇视、杭州宇泛的枪机、球机、半球、NVR、DVR等不同类型的监控设备,通过视频监控平台进行设备的管理,通过RTSP拉流的方案管理监…...
SpringBoot日志+SpringMVC+UUID重命名文件+Idea热部署
目录 【SpringBoot日志】 什么是日志,日志的作用 关于日志的基本信息,又有哪些呢? 关于日志的级别 Springboot内置SLF4J【门面模式】 和 logback【日志框架】 在配置文件中可以设置日志级别【以.yml为例】 SpringBoot 持久化的保存日…...

向日葵远程控制中的键盘异常问题
本文记录的是ubuntu 20.04 上, 向日葵的最高版本目前只有V 11.0.1.44968(2022.02) 我的被控制和 控制端都是上述环境; 起因,由于我昨天在控制端按下了 win/ 或者是其他的组合键 (具体哪个键盘确实没有注…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
