数据结构—线性表(下)
文章目录
- 6.线性表(下)
- (4).栈与队列的定义和ADT
- #1.ADT
- #2.栈的基本实现
- #3.队列的形式
- #4.队列的几种实现
- (5).栈与队列的应用
- #1.栈的应用
- i.后缀表达式求值
- ii.中缀表达式转后缀表达式
- #2.队列的应用
- (6).线性表的其他存储方式
- #1.索引存储
- #2.哈希存储
- i.什么是哈希存储
- ii.碰撞了怎么办
- iii.这个散列函数,怎么设计呢?
- (7).查找
- #1.线性查找
- #2.二分查找
- 小结
6.线性表(下)
(4).栈与队列的定义和ADT
#1.ADT
上面说的链表和数组都是几乎没有限制的线性表结构,接下来我们就提一提两种受限制的线性表结构——栈和队列,它们的ADT是这样的:
ADT Stack {
数据对象: D = a i ∣ a i ∈ E l e m S e t , i = 0 , 1 , 2 , . . . , n − 1 , n ≥ 0 D = {a_i|a_i \in ElemSet, i=0,1,2,...,n-1, n\ge0} D=ai∣ai∈ElemSet,i=0,1,2,...,n−1,n≥0
数据关系: R = { < a i − 1 , a i > ∣ a i ∈ D , i = 1 , 2 , . . . , n − 1 , n ≥ 0 } R = \{<a_{i-1},a_i>|a_i \in D, i=1,2,...,n-1, n \ge 0\} R={<ai−1,ai>∣ai∈D,i=1,2,...,n−1,n≥0}, a n − 1 a_{n-1} an−1为栈顶, a 0 a_0 a0为栈底
基本操作: 初始化、进栈、出栈、取栈顶元素等
}
ADT Queue {
数据对象: D = { a i ∣ a i ∈ E l e m S e t , i = 0 , 1 , . . . , n − 1 , n ≥ 0 } D = \{a_i|a_i\in ElemSet, i = 0, 1, ..., n-1, n\ge 0\} D={ai∣ai∈ElemSet,i=0,1,...,n−1,n≥0}
数据关系: R = { < a i − 1 , a i > ∣ a i − 1 , a i ∈ D , i = 1 , 2 , . . . , n − 1 } R = \{<a_{i-1}, a_i>|a_{i-1},a_i\in D, i = 1,2,..., n-1\} R={<ai−1,ai>∣ai−1,ai∈D,i=1,2,...,n−1},约定其中 a 1 a_1 a1端为队列头, a n a_n an端为队列尾
基本操作:初始化、入队、出队、获得头元素、清空等
}
#2.栈的基本实现
栈是一种后进先出(Last In First Out, LIFO) 的数据结构,听起来,你想实现一个基本的栈相当简单啊,比如这就是个例子:
#include <cstring>struct stack
{int* _data;int _capacity;int _top;stack(): _data(nullptr), _capacity(0), _top(0) {}stack(const int _cap): _data(new int[_cap] {0}), _capacity(_cap), _top(0) {}stack(const stack& s): _data(new int[_capacity] {0}), _capacity(s._capacity), _top(s._top){memcpy(_data, s._data, _top * sizeof(int));}~stack(){delete[] _data;_data = nullptr;}bool empty() const{return (_top == 0);}void push(const int& val){if (_top < _capacity) {_data[_top++] = val;}else {std::cout << "Stack Full!" << std::endl;}}int pop(){if (!empty()) {int rt{ _data[--_top] };return rt;}else {std::cout << "Stack Empty!" << std::endl;return -1;}}int top() const{if (!empty()) {return _data[_top];}else {std::cout << "Stack Empty!" << std::endl;return -1;}}int size() const{return _top + 1;}
};
相当简单,用一个很简单的数组就可以完成模拟了,因为它的入和出操作都是在末尾,因此不需要涉及到数据的频繁移动。
#3.队列的形式
但是队列可就不一样了,队列是一种先进先出(First In First Out, FIFO) 的数据结构,如果我们简单用一个数组来模拟,那我们从数组的最后入队,再从数组的头出队,这样一次操作之后我们可能需要把后面所有的数字都往前移动一位,这样的性能是很低的:
因此基于数组的队列,我们一般采取环形队列的思路来实现,然后你会发现,这个数据结构对于链式存储的线性表来说,好像实现起来非常容易—因为我们不管是在头还是尾插入都不需要对后面的数据进行移动操作,所以链式存储结构不仅可以实现队列,还可以实现双端队列,也就是在头和尾都可以进行入队、出队的队列。
还有一种则是优先队列,它的出队顺序不是依照入队顺序来的,它的顺序是依照我们预先对于数据的顺序进行出队,例如我们按照整数大小作为优先顺序,那么输入:7, 10, 4, 8, 3, 2, 3, 9, 2, 6,入队之后再依次出队的结果就是:2, 2, 3, 3, 4, 6, 7, 8, 9, 10,哇哦,输出的顺序就变成有序了,这就是一种排序了,再偷偷告诉你,这个排序算法的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn) ,那么这么好的队列我们要怎么实现呢?我们只要用堆就可以实现了! 所以我等会儿可以给你提供一段代码,但我不会细讲,具体的内容要等到后面的树篇才能讲到了。
#4.队列的几种实现
首先是顺序存储实现的循环队列:
struct queue
{int* _data;int _capacity;int _size;int _head;queue(): _data(nullptr), _capacity(0), _size(0), _head(0) {}queue(const int capa): _data(new int[capa] {0}), _capacity(capa), _size(0), _head(0) {}queue(const queue& q): _data(new int[q._capacity]), _capacity(q._capacity), _size(q._size), _head(q._head){memcpy(_data, q._data, _size * sizeof(int));}~queue(){delete[] _data;_data = nullptr;}bool empty() const{return (_size == 0);}void enqueue(const int val){if (_size < _capacity) {_data[(_head + _size) % _capacity] = val;_size++;}else {std::cout << "Queue Full!" << std::endl;}}int dequeue(){if (!empty()) {_size--;int rt{ _data[_head] };_head = (_head + 1) % _capacity;return rt;}else {std::cout << "Queue Empty!" << std::endl;return -1;}}int first() const{if (!empty()) {return _data[_head];}else {std::cout << "Queue Empty!" << std::endl;return -1;}}
};
还算简单,只是在计算访问和插入的下标时,要注意使用取余来保证我们的数据是循环地存在整个数组当中的,这样的做法可以有效避免多次数据的移动,从而增加队列的效率,不过这种队列还是有存储空间限制的,有点讨厌,用链式存储实现的队列一般来说就不会有这个问题。
然后是链式存储实现的队列/双端队列:
struct deque
{list _data;int _size;deque(): _data(), _size(0) {}deque(const deque& dq): _data(dq._data), _size(dq._size) {}~deque() = default;bool empty() const{return (_size == 0);}void push_front(const int val){_data.push_front(val);_size++;}void push_back(const int val){_data.push_back(val);_size++;}int pop_front(){if (!empty()) {int rt{ _data.front() };_data.pop_front();_size--;return rt;}else {std::cout << "Deque Empty!" << std::endl;return -1;}}int pop_back(){if (!empty()) {int rt{ _data.back() };_data.pop_back();_size--;return rt;}else {std::cout << "Deque Empty!" << std::endl;return -1;}}int back() const{if (!empty()) {return _data.back();}else {std::cout << "Deque Empty!" << std::endl;return -1;}}int front() const{if (!empty()) {return _data.front();}else {std::cout << "Deque Empty!" << std::endl;return -1;}}
};
如果你的链表功能已经实现的很完全了,那么这个双端队列的实现就要多简单有多简单了,只要插插头、插插尾就可以了,双端队列就是在头和尾都可以进行入队和出队的队列,你想只实现一个正常的队列,其实也是一样的,把front的系列函数都去掉就好了。
最后是优先队列:
template<typename T>
class heap
{// Small root heap
public:vector<T> data;size_t size;heap(){size = 0;}heap(vector<T> nums){// 99 5 36 7 22 17 46 12 2 19 25 28 1 92this->data = nums;this->size = nums.size() - 1;for (size_t i = size / 2; i >= 1; i--) {siftdown(i);}}void siftup(size_t i){bool check = false;if (i == 1) return;else {while (i != 1 && !check) {if (this->data[i] < this->data[i / 2]) {T temp = this->data[i / 2];this->data[i / 2] = this->data[i];this->data[i] = temp;i /= 2;}else check = true;}}return;}void siftdown(size_t i){bool check = false;size_t t = 0;while (i * 2 <= this->size && !check) {if (this->data[i] > this->data[i * 2]) {t = i * 2;}else t = i;if (i * 2 + 1 <= this->size) {if (this->data[t] > this->data[i * 2 + 1]) {t = i * 2 + 1;}}if (t != i) {T temp = this->data[t];this->data[t] = this->data[i];this->data[i] = temp;i = t;}else {check = true;}}return;}T deletemin(){T temp = this->data[1];this->size--;this->data[1] = this->data[this->size];siftdown(1);return temp;}void addElement(T num){this->data.push_back(num);this->size++;siftup(this->size);}void heap_sort(){heap<T> h_temp{ *this };while (h_temp.size > 1) {cout << h_temp.deletemin() << " ";}cout << endl;}bool empty(){if (this->size == 0) return true;else return false;}template<typename U>friend ostream& operator<<(ostream& output, heap<U>& h){size_t n = 1;for (size_t i = 1; i <= h.size; i++) {output << h.data[i] << " ";if (i == n * 2 - 1) {output << endl;n *= 2;}}output << endl;return output;}~heap(){this->data.~vector();this->size = 0;}
};
优先队列依靠的堆是一种完全二叉树,在序号前一个节点未被填充的情况下,后一个节点是不能被填充的,因此用数组存这棵树不会有空间的浪费,并且相较于采取二叉树一般的两个子节点的存法,这种实现方法更加简单,不过具体的,等到我们的树篇再详细介绍吧。
(5).栈与队列的应用
说完了实现,接下来就看看栈和队列有什么用吧。栈和队列实际上是对我们生活中的某些有固定存取顺序的问题的一个模拟数据类型,例如栈就像堆在一起的盘子,我们把盘子从下面一个个往上堆,最先取出的只能是最上面的那个(不然盘子塔就塌了,这不好),还有是队列,这个更好说,我们平时排队的时候就是这么做的,人从最后进来,然后从最前面出去,中间需要进行排队等待。
#1.栈的应用
计算机内存的栈区实际上也是将内存依照栈的方式排布的,对于我们来说,有了栈的结构,想要完成函数的相互调用就很容易了,我们把一个函数所需要的参数、调用的基本指令占用的栈区的所有部分称为栈帧,那么调用某个函数的过程就可以简单描述为:传入参数、建立栈帧、调用指令处理数据、消去栈帧、回传数据,这也支持了我们现在的编程语言的一般思路:函数里调用另一个函数,会暂停当前函数,先继续完成被调用函数,直到调用链到头,再开始回溯。
这也保证了我们C++中的Stack Unwinding流程可以顺利进行,Stack Unwinding是C++的遇到异常时会进行的自动释放资源的一套流程,这保障了RAII机制的稳定运行。
i.后缀表达式求值
好了好了,扯远了,有一些比较经典的问题可以用栈来解决,在这里我们举一个后缀表达式求值的例子,它的基本情况是这样的:
我们常见的数学表达式是形如 ( 1 + 3 ) × 5 ÷ 6 + 41 × ( 2 + 451 ) (1+3)\times 5\div 6+41\times (2+451) (1+3)×5÷6+41×(2+451)这样的,但是括号的出现以及运算符优先级带来了很多不确定性,因此我们在计算机中习惯性地会采用前缀表达式或后缀表达式来表示数学表达式,这里我们介绍一下后缀表达式的基本形式: n u m 1 n u m 2 o p num1 \ num2 \ op num1 num2 op,如 3 4 + 3 \ 4 \ + 3 4 +, 12 41 / 12 \ 41 \ / 12 41 /,这样的,前面两个作为操作数,后面的符号是要进行的运算符,使用前缀或后缀表达式的好处就在于:它们不需要括号可以表达优先级,这样一来,问题的处理会变得很简单
接下来你要尝试接收一个长度不超过100个字符的字符串,其中存在若干个0~9之间的操作数以及若干操作符,其中不会出现除以0或操作数对应失败等非法操作,你要做的是,求出这个后缀表达式的值(整数计算)。
乍一看你好像并不知道怎么操作这个东西,但是你可以先试试算一下这个式子,告诉我结果是多少: 3 3 4 5 × + × 6 − 9 4 ÷ + 3\ 3\ 4\ 5\ \times\ +\ \times\ 6\ -\ 9\ 4\div+ 3 3 4 5 × + × 6 − 9 4÷+,算出来了吗?结果是65,计算过程是什么样的呢,我们一步步看看:
- 1.接收3、3、4、5直到遇到 × \times ×,然后把4和5做一个乘法得到20,再塞回去就是3、3、20
- 2.遇到 + + +,把3和20做一个加法得到23,塞回去:3、23
- 3.遇到 × \times ×,把3和23做一个乘法得到69,塞回去69
- 4.接下来继续接收6,又遇到了-,把69和6做一个减法得到63,塞回去63
- 5.接下来接收9、4,又遇到了 ÷ \div ÷,把9和4做一个整除得到2,塞回去63、2
- 6.最后接收到了 + + +,把63和2做一个加法得到65,表达式结束
- 结果就是65
所以我们的计算流程主要就是这么两步:接收输入,如果是数字就存一下,如果是符号就取数字做计算、把计算结果存回去,而且我们会发现,取数字和存数字的顺序是后进先出的,也就是说,我们可以使用一个栈来存下这些数字,所以我们就可以得到以下的代码:
int calculate(const string& RPN)
{stack<int> s;for (int i = 0; i < RPN.size(); i++) {if (isdigit(RPN[i])) {s.push(RPN[i] - '0');}else {int num1{ 0 }, num2{ 0 };num2 = s.top();s.pop();num1 = s.top();s.pop();switch (RPN[i]) {case '+':s.push(num1 + num2);break;case '-':s.push(num1 - num2);break;case '*':s.push(num1 * num2);break;case '/':s.push(num1 / num2);break;}}}return s.top();
}
输入的表达式中每个操作符和运算数之间没有多余的空格,效果如下:

很好,效果和我们想的一样,不过一般的表达式可能会更复杂,包括:包含超过1位的数字,包含负号等,这里给出一个更加完善的后缀表达式求解的函数:
int calculate(const string& RPN)
{stack<int> s;int temp{ 0 };bool num{ false };for (int i = 0; i < RPN.size(); i++) {if (isdigit(RPN[i])) {temp *= 10;temp += RPN[i] - '0';num = true;}else if (!isdigit(RPN[i])) {if (RPN[i] == ' ') {if (num) {num = false;s.push(temp);temp = 0;}continue;}if (RPN[i] == '~') {int num = s.top();s.pop();s.push(-num);}else {int num1{ 0 }, num2{ 0 };num2 = s.top();s.pop();num1 = s.top();s.pop();if (RPN[i] == '+') s.push(num1 + num2);else if (RPN[i] == '-') s.push(num1 - num2);else if (RPN[i] == '*') s.push(num1 * num2);else if (RPN[i] == '/') s.push(num1 / num2);}}}return s.top();
}
这里用~表示负号,主要是因为负号的出现可能导致后缀表达式出现二义性,例如: − 3 − ( − 4 − 5 ) − ( − 5 ) ⇒ 3 − 4 − 5 − − 5 − − -3-(-4-5)-(-5) \Rightarrow 3-4-5--5-- −3−(−4−5)−(−5)⇒3−4−5−−5−−,然后看看我们的解析流程,这里声明一下,如果从栈中只能获得一个数字,那么把负号认为是单目的负号而不是减号:
- 1.接收3,遇到 − - −,栈里只有一个数字,操作把-3放回栈中
- 2.接收4,遇到 − - −,栈里有-3, 4,那么计算得到-7,放回栈
- 3.接收5,遇到 − - −,栈里有-7, 5,那么计算得到-12,放回栈
- 4.遇到 − - −,栈里只有一个数字,操作把12放回栈中
- 5.接收5,遇到 − - −,栈里有12, 5,那么计算得到7,放回栈
- 6.遇到 − - −,栈里只有一个数字,操作把-7放回栈中,读取结束
- 结果为-7
你再看看,这个结果对吗? − 3 − ( − 4 − 5 ) − ( − 5 ) -3-(-4-5)-(-5) −3−(−4−5)−(−5)的结果应该是11而不是-7,因此单一的负号并不具备在后缀表达式中同时表达取负和减法两种功能的能力,所以在这里我们用~来表示负号,你可以自己尝试一下。
ii.中缀表达式转后缀表达式
还是回到前面的问题,现在我们的问题不再是把这个表达式的值求出来了,而是说:我们平时用的都是中缀表达式,让我把中缀表达式转后缀表达式还有点麻烦呢,能不能让计算机直接给我算出来呢? 你可以按Windows + R,然后输入calc,敲一下回车,就可以算出来了
哈你当然不能在解决实际问题的时候让别人这么做,所以我们得想想,我们自己是怎么把中缀表达式计算成后缀表达式的,比如 3 × 4 3\times 4 3×4,那么结果很简单就是 3 4 × 3\ 4\ \times 3 4 ×,如果是 3 + 4 × 5 3+4\times5 3+4×5,那么首先这里优先级最高的是 × \times ×,所以碰到3直接输出,然后碰到 + + +也暂存起来,碰到4又直接输出,然后碰到了 × \times ×,这次的优先级比上次的 + + +更高,继续下去又碰到了5,直接输出,然后遍历完了,再逐渐出栈,最后就得到了 3 4 5 × + 3\ 4 \ 5 \times\ + 3 4 5× +,这就对了!
所以我们好像知道方法了,在遍历的过程中:只要碰到数字就输出、碰到符号就去比较栈,如果栈空或者栈顶符号优先级比现在符号优先级低,就入栈;如果比现在符号优先级高,就把栈顶输出,然后再入栈,所以代码就写出来了:
void ToRPN(const string& origin)
{stack<char> ch;bool isInner{ false };for (const auto& i : origin) {if (isdigit(i)) {cout << i;}else {if (ch.empty()) ch.push(i);else {if (i != ')') {if (i == '(') {ch.push(i);isInner = true;}else if (!ch.empty() && cmp(i, ch.top()) > 0 || (!isdigit(i) && isInner && ch.top() == '(')) {ch.push(i);}else {while (!ch.empty() && ch.top() != '(' && cmp(i, ch.top()) <= 0) {if (ch.top() != '(') cout << ch.top();ch.pop();}ch.push(i);}}else {while (!ch.empty() && ch.top() != '(') {cout << ch.top();ch.pop();}if (!ch.empty()) ch.pop();isInner = false;}}}}while (!ch.empty()) {cout << ch.top();ch.pop();}
}int transform(char c)
{switch (c) {case '+':case '-':return 1;case '*':case '/':return 2;case '^':return 3;case '(':return 4;case ')':return 5;default:return -1;}
}// c1 > c2 return > 0, c1 == c2 return 0, else return < 0
int cmp(char c1, char c2)
{int a{ transform(c1) }, b{ transform(c2) };return a - b;
}
这么做其实写代码不难,关键在于符号之间的优先级应该怎么界定,在这里我们用了一个转换再比较的方式得到结果,±优先级相同且最低,然后是*/,然后是^,之后是括号,这样就做出来了,看看结果:

就是这样,不过现在这个函数还不能接收多位数字和负号(这里指的是i中提到的负号的二义性问题)的输入,因此我们“稍微”改造一下就好了:
string ToRPN(const string& origin)
{string ans;stack<char> ch;bool isInner{ false };bool lastNum{ false };bool isNegative{ true };for (const auto& i : origin) {if (isdigit(i)) {ans.push_back(i);lastNum = true;}else {if (lastNum) {lastNum = false;isNegative = false;ans.push_back(' ');}if (ch.empty()) {if (i == '-' && !isInner && ans.empty()) ch.push('~');else {ch.push(i);if (i == '(') isInner = true, isNegative = true;}}else {if (i != ')') {if (i == '(') {ch.push(i);isNegative = true;isInner = true;}else if (!ch.empty() && (cmp(i, ch.top()) > 0 || (!isdigit(i) && isInner && ch.top() == '('))) {if (ch.top() == '(' && isNegative && i == '-') ch.push('~');else ch.push(i);}else {while (!ch.empty() && ch.top() != '(' && cmp(i, ch.top()) <= 0) {if (ch.top() != '(') {ans.push_back(ch.top());ans.push_back(' ');}ch.pop();}ch.push(i);}}else {while (!ch.empty() && ch.top() != '(') {ans.push_back(ch.top());ans.push_back(' ');ch.pop();}if (!ch.empty()) ch.pop();isInner = false;}}}}if (lastNum) ans.push_back(' ');while (!ch.empty()) {ans.push_back(ch.top());ans.push_back(' ');ch.pop();}return ans;
}int transform(char c)
{switch (c) {case '+':case '-':return 1;case '*':case '/':return 2;case '~':return 3;case '^':return 4;case '(':return 5;case ')':return 6;default:return -1;}
}// c1 > c2 return > 0, c1 == c2 return 0, else return < 0
int cmp(char c1, char c2)
{int a{ transform(c1) }, b{ transform(c2) };return a - b;
}
稍微嘛、、稍微修改,这个代码会稍微复杂一点,你可以自己试着写一遍,然后再来对对答案,其实不会很困难,而且做出来之后会很有意思
现在,你已经可以把中缀表达式转后缀表达式,又可以求出后缀表达式的值了,把它们结合一下,就可以实现中缀表达式求值了,下面是一个例子:
#include <iostream>
#include <cctype>
#include <stack>
#include <string>
using namespace std;
const char c[]{ '+', '-', '*', '/', '(', ')', '~' };string ToRPN(const string& origin);
int transform(char c);
int cmp(char c1, char c2);
int calculate(const string& RPN);int main()
{string temp;cin >> temp;// cout << ToRPN(temp);cout << calculate(ToRPN(temp));return 0;
}string ToRPN(const string& origin)
{string ans;stack<char> ch;bool isInner{ false };bool lastNum{ false };bool isNegative{ true };for (const auto& i : origin) {if (isdigit(i)) {ans.push_back(i);lastNum = true;}else {if (lastNum) {lastNum = false;isNegative = false;ans.push_back(' ');}if (ch.empty()) {if (i == '-' && !isInner && ans.empty()) ch.push('~');else {ch.push(i);if (i == '(') isInner = true, isNegative = true;}}else {if (i != ')') {if (i == '(') {ch.push(i);isNegative = true;isInner = true;}else if (!ch.empty() && (cmp(i, ch.top()) > 0 || (!isdigit(i) && isInner && ch.top() == '('))) {if (ch.top() == '(' && isNegative && i == '-') ch.push('~');else ch.push(i);}else {while (!ch.empty() && ch.top() != '(' && cmp(i, ch.top()) <= 0) {if (ch.top() != '(') {ans.push_back(ch.top());ans.push_back(' ');}ch.pop();}ch.push(i);}}else {while (!ch.empty() && ch.top() != '(') {ans.push_back(ch.top());ans.push_back(' ');ch.pop();}if (!ch.empty()) ch.pop();isInner = false;}}}}if (lastNum) ans.push_back(' ');while (!ch.empty()) {ans.push_back(ch.top());ans.push_back(' ');ch.pop();}return ans;
}int transform(char c)
{switch (c) {case '+':case '-':return 1;case '*':case '/':return 2;case '~':return 3;case '^':return 4;case '(':return 5;case ')':return 6;default:return -1;}
}// c1 > c2 return > 0, c1 == c2 return 0, else return < 0
int cmp(char c1, char c2)
{int a{ transform(c1) }, b{ transform(c2) };return a - b;
}int calculate(const string& RPN)
{cout << RPN << endl;stack<int> s;int temp{ 0 };bool num{ false };for (int i = 0; i < RPN.size(); i++) {if (isdigit(RPN[i])) {temp *= 10;temp += RPN[i] - '0';num = true;}else if (!isdigit(RPN[i])) {if (RPN[i] == ' ') {if (num) {num = false;s.push(temp);temp = 0;}continue;}if (RPN[i] == '~') {int num = s.top();s.pop();s.push(-num);}else {int num1{ 0 }, num2{ 0 };num2 = s.top();s.pop();num1 = s.top();s.pop();if (RPN[i] == '+') s.push(num1 + num2);else if (RPN[i] == '-') s.push(num1 - num2);else if (RPN[i] == '*') s.push(num1 * num2);else if (RPN[i] == '/') s.push(num1 / num2);}}}return s.top();
}
这里的后缀表达式计算中没有考虑幂运算的操作,你可以试着完善一下。
#2.队列的应用
队列的应用主要还是在广度优先搜索(BFS) 中,这个等到图篇我们再细说。
(6).线性表的其他存储方式
这里主要提一提索引存储和哈希存储。
#1.索引存储
索引存储类似于分桶的思路,我们采取相对小数量的桶,给它们编号0~10,然后对于索引对10取余的结果,将结点存到对应的桶当中去,这个就不细说了,我们主要说一说哈希存储。
#2.哈希存储
i.什么是哈希存储
哈希(Hash)存储是根据存储内容的特性,经过散列函数H(x)计算得到一个在已分配存储空间上的位置,它的思路像是上面说的分桶存储的极限情况,这时候每个桶只存一个数据,这样做其实并不一定能充分利用空间,因为如果你的散列函数不能比较均匀地把数据映射到整个表中,即出现了很多哈希碰撞的情况,那么就会浪费非常多已经预先分配好的空间,比如我们的哈希函数如果简单如下:
H ( x ) = x % 10 H(x)=x\%10 H(x)=x%10
然后给你一堆11、21、31、41…这样以1结尾的数据,你就麻烦大了,所有的数据全都存到下标为1的分组下面去了,这样不仅浪费了别的空间,而且还得在同一个下标下不停地存,这样到最后查找数据就直接退化了,完全不能发挥哈希表的优势。
因此,哈希表并不是解决空间利用效率低的办法,而是加快查找速度的方法,只要你的散列函数不太复杂,时间复杂度为 O ( 1 ) O(1) O(1),那么在一个表里查找某个值的最优时间复杂度往往就是 O ( 1 ) O(1) O(1),如果有一个完美的散列函数,那么查找的平均和最坏时间复杂度也基本都是 O ( 1 ) O(1) O(1),当然我们做不到完美哈,不过哈希的效率的确是比较高的。
ii.碰撞了怎么办
那么如果碰到哈希碰撞的问题怎么办? 鉴于我们不能找到完美散列函数,所以我们需要一个解决碰撞的方法,一般来说是两种:开放寻址法和链地址法。
首先是开放寻址法,主要采取线性寻址。这个方法还蛮简单的,如果你经过散列函数得到的下标已经被占用了,那就往后找,一直找到下一个能存的位置再存,这个方法可能会导致哈希方法的退化,因为当前元素随手往后找一个,很有可能直接挤占了下一个元素的空间,导致后面的每一个元素都要往后找
然后是链地址法,这个要好一点,就是在碰撞之后,往当前地址的链后面加一个新的结点,类似于分桶查找,但是这么一来,就可以有效避免挤占别人空间的问题,效率真的会比线性寻址的方法更加高一点。
iii.这个散列函数,怎么设计呢?
鉴于你用的是C++,我们可以直接:
std::hash<int> hash;
std::cout << hash(214);
C++对于内置的类型,包括STL都提供了std::hash<T>,你可以直接调用,但是对于一些没有内置哈希函数的语言,比如C语言,我们可能得自己想个办法设计,在这里提供一种对于字符串的处理思路:将字符串作为一个大于26的素数进制的整数,将这个字符串还原为对应素数进制的十进制整数,再对哈希表大小取余,你可以这么操作:
int hash(const string& str)
{size_t size{ str.size() };int base{ 31 }, code{ str[0] };for (int i = 1; i < size; i++) {code *= base;code %= 100010;code += str[i];}return code % 100010;
}
为了避免越界,我们的结果要进行取余操作。
(7).查找
你知道我要说什么.jpg,没错,这一节我们就讲两种查找方式:线性查找和二分查找。
#1.线性查找
这个就很自然了,比如我们有一个未知顺序的线性表,我们可以:
// int to_find
int ans{ -1 };
for (int i = 0; i < v.size(); i++) {if (v[i] == to_find) {ans = i;break;}
}
它的时间复杂度是 O ( n ) O(n) O(n)。
#2.二分查找
二分查找的思路是每一次查找的过程中,把范围缩小一半,不过就缩小一半范围这个要求也挺困难的,这需要被查找的线性表有序,并且支持随机访问,因为我们的查找过程是需要经常发生跳转的,所以一般的链表采用二分查找并不能优化效率,这个之后我们再来说。
来看看代码吧,这个代码其实反而简单了:
int binary_search(const vector<int>& v, int val)
{int low{ 0 }, high{ v.size() - 1 }, mid{ 0 };while (low <= high) {mid = (low + high) / 2;if (v[mid] == val) return mid;else if (v[mid] > val) {high = mid - 1;}else low = mid + 1;}return -1;
}
最后来看看时间复杂度,我们设二分查找对于n个数据的操作次数为 T ( n ) T(n) T(n),那么应该有以下递推式:
T ( n ) = T ( n 2 ) + 1 = T ( n 4 ) + 2 = . . . = T ( n 2 k ) + k , ( n = 2 k ) = T ( 1 ) + log 2 n = log 2 n + 1 ⇒ O ( T ( n ) ) = O ( log n ) T(n) = T(\frac{n}{2})+1=T(\frac{n}{4})+2=...\\=T(\frac{n}{2^k})+k, (n = 2^k) = T(1) + \log_2 n=\log_2 n+1\\\Rightarrow O(T(n)) = O(\log n) T(n)=T(2n)+1=T(4n)+2=...=T(2kn)+k,(n=2k)=T(1)+log2n=log2n+1⇒O(T(n))=O(logn)
因此,我们证明了二分查找的时间复杂度是 O ( log n ) O(\log n) O(logn),所以它的效率真的很高,不过代码当中我们看到,我们总是要做v[mid]的操作,这对于链表来说是不能在 O ( 1 ) O(1) O(1)的时间复杂度内实现的,因此我们的递推式就会变成这样:
T ( n ) = T ( n 2 ) + n 2 + 1 = T ( n 4 ) + n 2 + n 4 + 2 = . . . = T ( n 2 k ) + ∑ i = 1 k n 2 i + k , ( n = 2 k ) = T ( 1 ) + n − n 2 k + k = n + log 2 n − 1 ⇒ O ( T ( n ) ) = O ( n ) T(n)=T(\frac{n}{2})+\frac{n}{2}+1=T(\frac{n}{4})+\frac{n}{2}+\frac{n}{4}+2=...\\ = T(\frac{n}{2^k}) + \sum_{i=1}^k\frac{n}{2^i}+k, (n=2^k) = T(1)+n-\frac{n}{2^k}+k=n+\log_2 n-1\\ \Rightarrow O(T(n)) = O(n) T(n)=T(2n)+2n+1=T(4n)+2n+4n+2=...=T(2kn)+i=1∑k2in+k,(n=2k)=T(1)+n−2kn+k=n+log2n−1⇒O(T(n))=O(n)
最后发现,就因为随机访问的时间复杂度是 O ( n ) O(n) O(n),所以对于链表的二分查找就从 O ( log n ) O(\log n) O(logn)退化成了 O ( n ) O(n) O(n)了。
最后提一下,我们还是需要知道如何计算时间复杂度的,对于前面的线性问题还比较好解决,对于这种递推式的,一般来说还可以采取主定理的方式来解决,它的基本内容如下:
假定有递推关系式 T ( n ) = a T ( n b ) + f ( n ) T(n)=aT(\frac{n}{b})+f(n) T(n)=aT(bn)+f(n),其中 n n n为问题规模, a a a为递推的子问题数量, n b \frac{n}{b} bn为每个子问题的规模(假设每个子问题的规模基本一样), f ( n ) f(n) f(n)为递推以外进行的计算工作。
a ≥ 1 , b > 1 a\ge1,b>1 a≥1,b>1为常数, f ( n ) f(n) f(n)为函数, T ( n ) T(n) T(n)为非负整数,则有:
(1).若 f ( n ) = O ( n log b a − ε ) , ε > 0 f(n)=O(n^{\log_b a-\varepsilon}),\varepsilon>0 f(n)=O(nlogba−ε),ε>0,那么 T ( n ) = Θ ( n log b a ) T(n)=\Theta(n^{\log_b a}) T(n)=Θ(nlogba), Θ \Theta Θ是同阶量的表示法
(2).若 f ( n ) = Θ ( n log b a ) f(n)=\Theta(n^{\log_b a}) f(n)=Θ(nlogba),那么 T ( n ) = Θ ( n log b a log n ) T(n)=\Theta(n^{\log_b a} \log n) T(n)=Θ(nlogbalogn)
(3).若 f ( n ) = Ω ( n log b a + ε ) , ε > 0 f(n)=\Omega(n^{\log_b a+\varepsilon}), \varepsilon>0 f(n)=Ω(nlogba+ε),ε>0,且对于某个常数 c < 1 c<1 c<1和所有充分大的 n n n有 a f ( n b ) ≤ c f ( n ) af(\frac{n}{b})\le cf(n) af(bn)≤cf(n),那么 T ( n ) = Θ ( f ( n ) ) T(n)=\Theta(f(n)) T(n)=Θ(f(n)), Ω \Omega Ω是高阶量的表示法1
例如对于快速排序,有以下递推式:
T ( n ) = 2 T ( n 2 ) + n , a = 2 , b = 2 , f ( n ) = n T(n)=2T(\frac{n}{2})+n,a=2,b=2,f(n)=n T(n)=2T(2n)+n,a=2,b=2,f(n)=n 根据主定理,则有:
T ( n ) = Θ ( n log n ) T(n)=\Theta(n\log n) T(n)=Θ(nlogn)
还挺简单,对吧?
小结
线性表的这一篇就到这里结束了,这算是数据结构的一个起点,下一章我们将介绍字符串的一些基本内容。
https://baike.baidu.com/item/主定理/3463232 ↩︎
相关文章:

数据结构—线性表(下)
文章目录 6.线性表(下)(4).栈与队列的定义和ADT#1.ADT#2.栈的基本实现#3.队列的形式#4.队列的几种实现 (5).栈与队列的应用#1.栈的应用i.后缀表达式求值ii.中缀表达式转后缀表达式 #2.队列的应用 (6).线性表的其他存储方式#1.索引存储#2.哈希存储i.什么是哈希存储ii.碰撞了怎么…...

apisix之插件开发,包含java和lua两种方式
https://download.csdn.net/download/tiantangpw/88475630 有ppt和springboot程序包,可以运行...
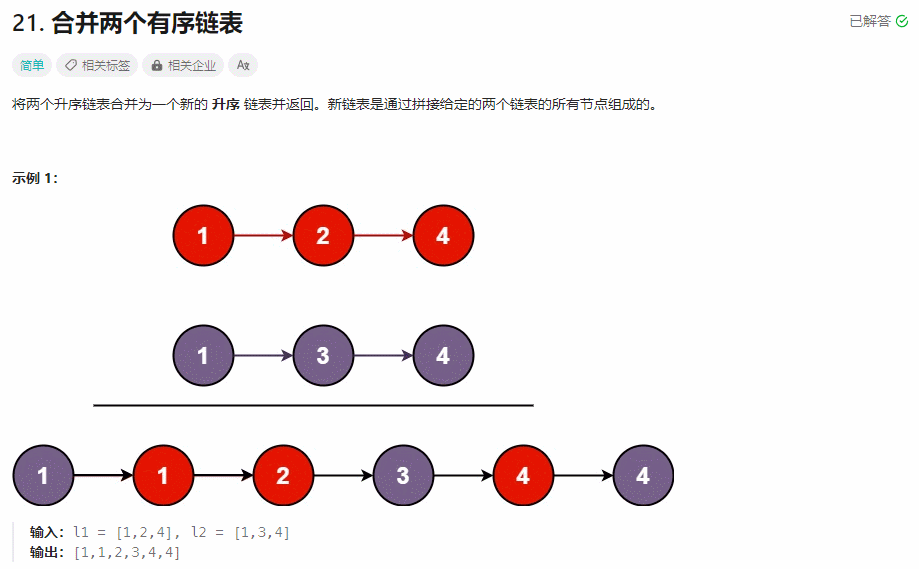
【面试经典150 | 链表】合并两个有序链表
文章目录 Tag题目来源题目解读解题思路方法一:递归方法二:迭代 写在最后 Tag 【递归】【迭代】【链表】 题目来源 21. 合并两个有序链表 题目解读 合并两个有序链表。 解题思路 一种朴素的想法是将两个链表中的值存入到数组中,然后对数组…...

【linux】麒麟v10安装Redis主从集群(ARM架构)
安装redis单示例的请看:麒麟v10安装Redis(ARM架构) 安装环境 HostnameIP addressmaster192.168.0.1slave1192.168.0.2slave2192.168.0.3 下载安装包 (三台都操作) wget https://repo.huaweicloud.com/kunpeng/…...

解决k8s删除名称空间无法强制删除的问题
问题起因:删除k8s名称空间的时候(此时名称空间下还有很多pod)一直删不掉,被我强行ctrl c了, 问题表象:然后就出现下面这悲催的一幕了,两个名称空间一直处于Terminating了 [rootmaster02 ~]# ku…...
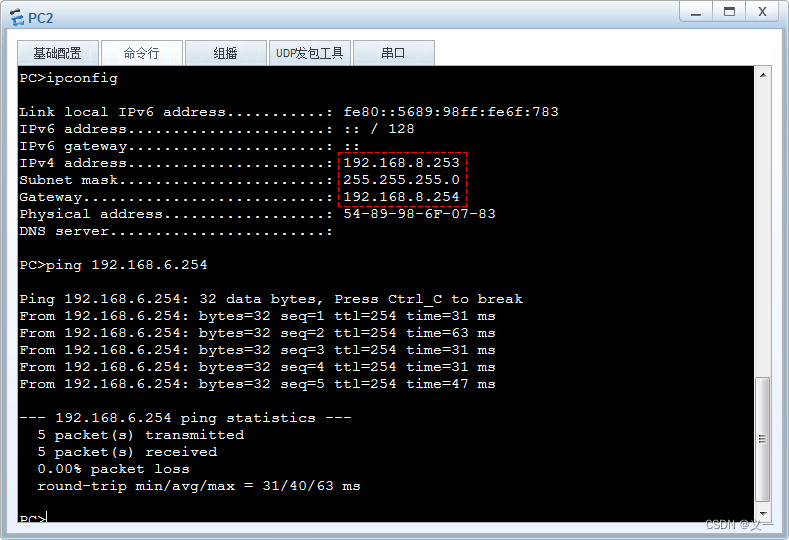
华为---DHCP中继代理简介及示例配置
DHCP中继代理简介 IP动态获取过程中,客户端(DHCP Client)总是以广播(广播帧及广播IP报文)方式来发送DHCPDISCOVER和DHCPREQUEST消息的。如果服务器(DHCP Server)和 客户端不在同一个二层网络(二…...

五、W5100S/W5500+RP2040树莓派Pico<UDP Client数据回环测试>
文章目录 1. 前言2. 协议简介2.1 简述2.2 优点2.3 应用 3. WIZnet以太网芯片4. UDP Client回环测试4.1 程序流程图4.2 测试准备4.3 连接方式4.4 相关代码4.5 测试现象 5. 注意事项6. 相关链接 1. 前言 UDP是一种无连接的网络协议,它提供了一种简单的、不可靠的方式来…...

死锁Deadlock
定义 死锁是指两个或多个线程互相持有对方所需的资源,从而导致它们无法继续执行的情况。如下图所示,现有两个线程,分别是线程A及线程B,线程A持有锁A,线程B持有锁B。此时线程A想获取锁B,但锁B需等到线程B的结…...

【spark客户端】Spark SQL CLI详解:怎么执行sql文件、注释怎么写,支持的文件路径协议、交互式模式使用细节
文章目录 一. Spark SQL Command Line Options(命令行参数)二. The hiverc File1. without the -i2. .hiverc 介绍 三. 支持的路径协议四. 支持的注释类型五. Spark SQL CLI交互式命令六. Examples1. running a query from the command line2. setting Hive configuration vari…...
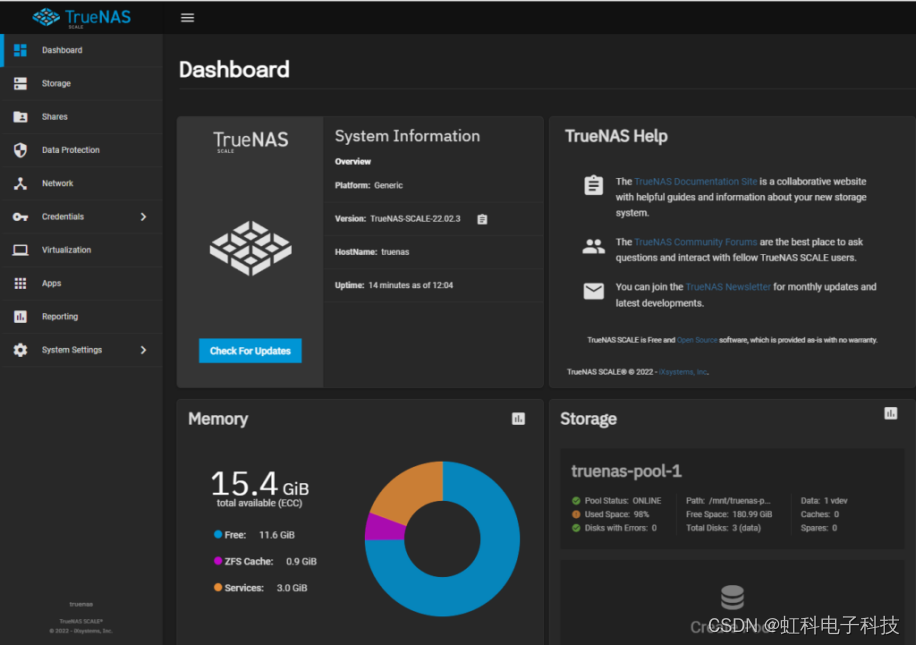
虹科干货 | HK-TrueNAS版本大揭秘!一文教您如何选择合适的TrueNAS软件
文章来源:虹科网络基础设施 阅读原文:https://mp.weixin.qq.com/s/Iv0zDDmiDgE9vEGlAZs-sg 1.导语 TrueNAS是虹科iXsystems 设计和开发的NAS 操作系统,提供许多功能,例如文件存储、虚拟机 (VM) 和媒体服务器。它基于…...

前端html+css+js实现的2048小游戏,很完善。
源码下载地址 支持:远程部署/安装/调试、讲解、二次开发/修改/定制 逻辑用的是JavaScript,界面用canvas实现,暂时还没有添加动画。 视频浏览地址...

学习通签到
要在Vue中使用H5lock.js,首先需要将H5lock.js引入到项目中。可以通过以下步骤来使用: 1. 将H5lock.js文件保存到项目中的某个目录下,例如src/assets文件夹。 2. 在需要使用H5lock.js的组件中,通过import语句将H5lock.js引入进来…...
target采退、测评养号购物下单操作教程
1.点击右上角的Create account注册账号 2.填写账号信息 3. 进入自己需要购买的商品页面 点击pick it up购买 4. 进入购物车页面选择快递方式和地址后点击 check out按钮 5. 之后会提示绑定XYK,这里我是用虚拟XYK开卡平台进行支付的. 6. 确认订单无误后点击Place you…...

SEACALL海外呼叫中心系统的优势包括
SEACALL海外呼叫中心系统的优势包括 封卡封号问题解决 海外呼叫中心系统通过API开放平台能力,定制电话营销系统,提供多项功能如自动拨打、智能应答、真人语音交互等,帮助企业克服员工离职率高、客户资源流失严重等挑战。 - 高级管理者操控 …...

Painter:使用视觉提示来引导网络推理
文章目录 1. 论文2. 示意图3. 主要贡献4. 代码简化 1. 论文 paper:Images Speak in Images: A Generalist Painter for In-Context Visual Learning github:https://github.com/baaivision/Painter 2. 示意图 3. 主要贡献 在 In-context Learning 中,作为自然语言…...

Fedora Linux 38 安装数学动画制作工具manimgl工具包
manimgl可以制作数学动画,它使用的是Python编程语言。 这里介绍他在Fedora Linux 38下的安装过程。 1. sudo dnf update 2. sudo dnf install python3-devel python3-pip python3-tools -y 3. sudo dnf install python3-numpy python3-scipy python3-sympy -y …...
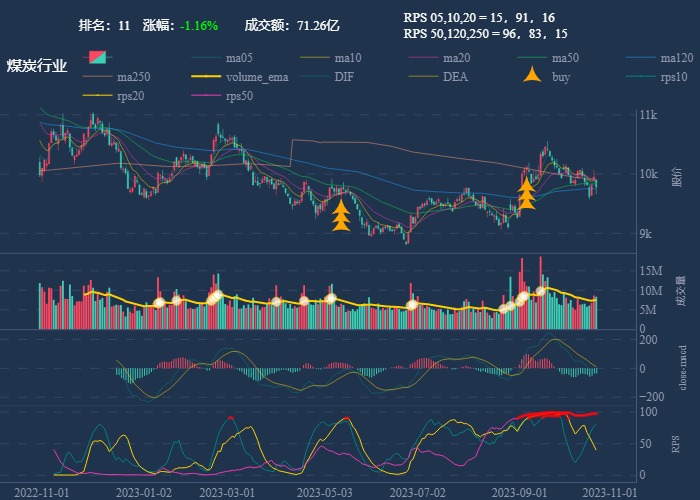
行业追踪,2023-10-26
自动复盘 2023-10-26 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
Android 和 iOS APP 测试的那些区别
目前市面上主流的移动操作系统就是 Android 和 iOS 两种,移动端测试本身就跟 Web 应用测试有自己的专项测试,比如安装、卸载、升级、消息推送、网络类型测试、弱网测试、中断测试、兼容性测试等都是区别于 Web 应用需要关注的测试领域。 那么࿰…...
利用nicegui开发ai工具示例
from fastapi import FastAPI import uvicorn from nicegui import uiclass PipRequirement:def __init__(self):ui.label("依赖安装与依赖展示")class BasicSettings:def __init__(self):self.project_select ui.select(["test"], label"项目选择&q…...

HarmonyOS鸿蒙原生应用开发设计- 流转图标
HarmonyOS设计文档中,为大家提供了独特的流转图标,开发者可以根据需要直接引用。 开发者直接使用官方提供的流转图标内容,既可以符合HarmonyOS原生应用的开发上架运营规范,又可以防止使用别人的图标侵权意外情况等,减…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
