保姆级认识AVL树【C++】(精讲:AVL Insert)
目录
前言
一,概念
二,定义
三,insert
1. 插入情况
情况一:
情况二:
情况三:
2. 旋转方法
法一:左单旋法
法二:右单旋法
法三:先左后右双旋法
法四:先右后左双旋法
测试(判断一棵树是否是AVL树)
代码如下:
3. 随机值案例
四,删除

前言
搜索二叉树请查看本篇博文:【C++】搜索二叉树底层实现_花果山~程序猿的博客-CSDN博客
一,概念
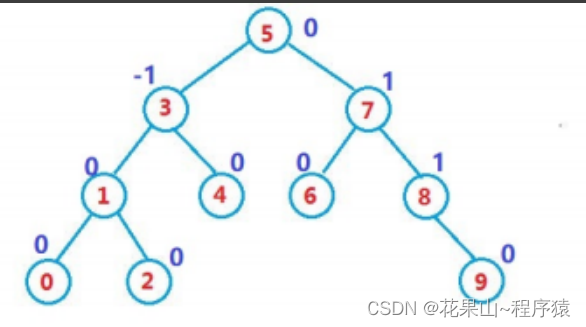
二,定义
为方便循序渐进的学习,这里只放最出初始的树结点定义。
template <class K, class V>
class AVL_Data
{
public:pair<K, V> _kv;AVL_Data<K, V>* left = nullptr;AVL_Data<K, V>* right = nullptr;AVL_Data<K, V>* parent = nullptr;int _bf = 0; // ballance factorAVL_Data(const pair<K, V>& p):_kv(p){}};
上面定义在后面会进行完善修改。
三,insert
根据前面搜索二叉树的经验我们能快速写完插入函数,但AVL树是特殊的搜索二叉树,我们需要对树的高度进行调整。那么我们插入时就会遇到三种情况:
1. 插入情况
情况一:

情况二:
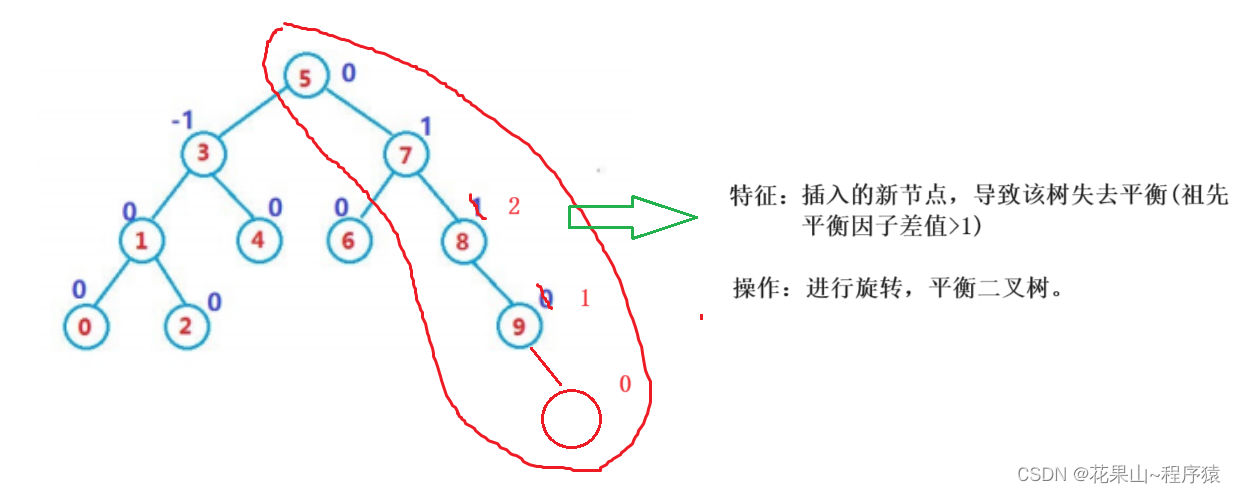
情况三:

代码实现如下:
template <class K, class V>
class AVL_Tree
{typedef AVL_Data<K, V> AVL_Data;AVL_Data* root = nullptr;public:bool insert(const pair<K, V>& p){AVL_Data* new_a_d = new AVL_Data(p);if (!root){root = new_a_d;}else{AVL_Data* cur = root;AVL_Data* parent = nullptr;while (cur){if (p.first < cur->_kv.first){parent = cur;cur = cur->left;}else if (p.first > cur->_kv.first){parent = cur;cur = cur->right;}else{delete(new_a_d); // 插入失败,删除新建结点return false;}}if (p.first < parent->_kv.first){parent->left = new_a_d;}else{parent->right = new_a_d;}new_a_d->parent = parent;cur = new_a_d;//完成插入,进行平衡while (parent){ // 插入,修改parent平衡因子if (cur == parent->right){parent->_bf++;}else{parent->_bf--;}// 判断parent平衡因子是否是0,如果非0则需要向祖先更新平衡因子if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->parent;}else if (parent->_bf == 0){break;}else if(parent->_bf == 2 || parent->_bf == -2){ // 处理绝对值大于1,下面代码目的是记录未修改的平衡因子。// 需要旋转处理,这个我们下面再讲cur = parent;parent = parent->parent;}else{// 出现其他情况,在插入时这棵AVL树本身就是异常AVL树assert(false);}}return true;}}
};2. 旋转方法
法一:左单旋法
我们以下面图为讲解例子,a,b,c表示的是子树。
h 表示子树的高度。
请看下面场景:
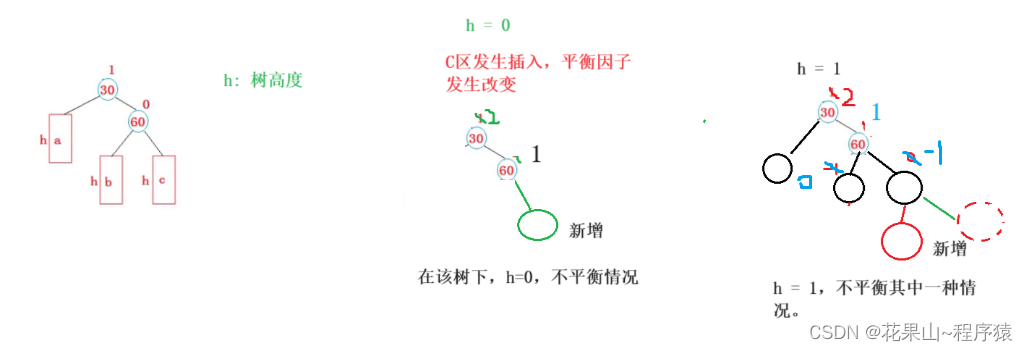

h = 3, 4...组合方式会更多,这里画出图没什么意义,问题是失去平衡我们如何解决??
通过下面方法解决:
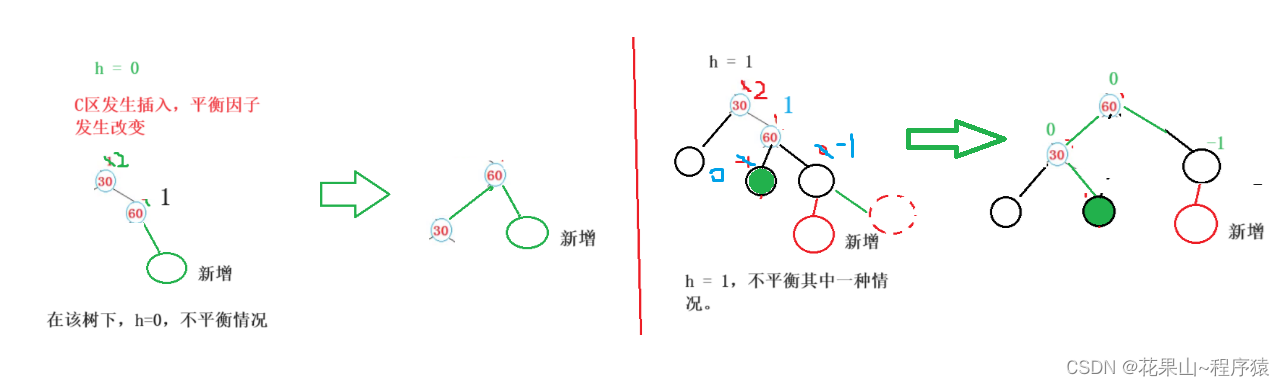
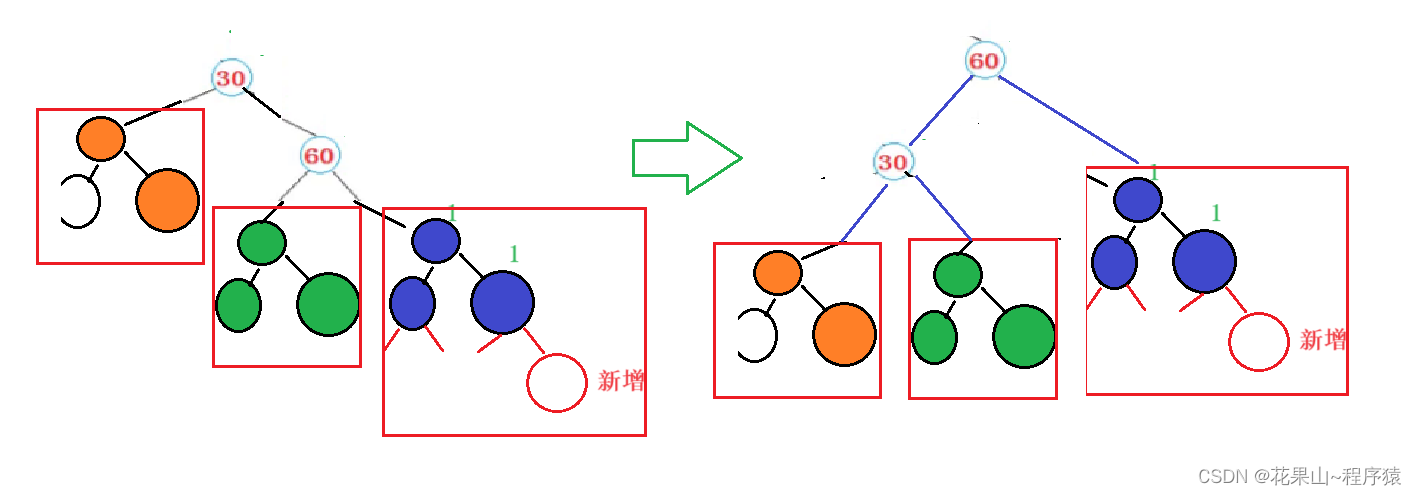
总结:
1. 右边高,则向左旋转。
2. C树发生插入,平衡因子发生改变,进而发生旋转。
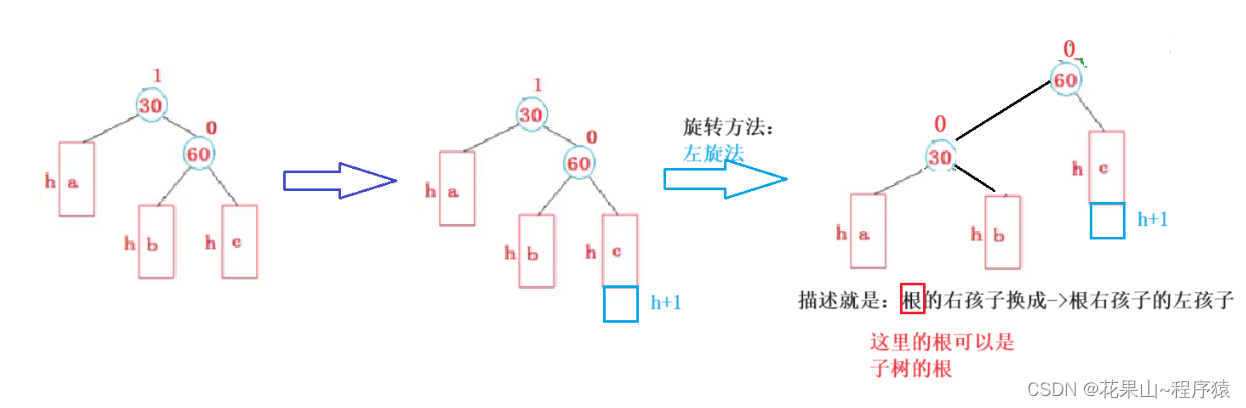
void RotateL(AVL_Data* parent){assert(parent->right);AVL_Data* par = parent;AVL_Data* par_R = par->right;AVL_Data* par_RL = par->right->left;AVL_Data* ppnode = par->parent;par->right = par_RL;if (par_RL)par_RL->parent = par;par_R->left = par;par->parent = par_R;par_R->parent = ppnode;if (!ppnode){root = par_R;}else if (ppnode->left == par){ppnode->left = par_R;}else{ppnode->right = par_R;}par->_bf = 0;par_R->_bf = 0;}// 实验例子AVL_Tree<int, string> tree;tree.insert(make_pair(30 , "李四"));tree.insert(make_pair(20, "二麻子"));tree.insert(make_pair(60, "张三"));tree.insert(make_pair(45, "王五"));tree.insert(make_pair(75, "王五"));tree.insert(make_pair(65, "王五"));
法二:右单旋法
思路跟左旋法差不多,图像是相反,这里就只给场景解法模板:

h = 0, 1, 2的发生场景:
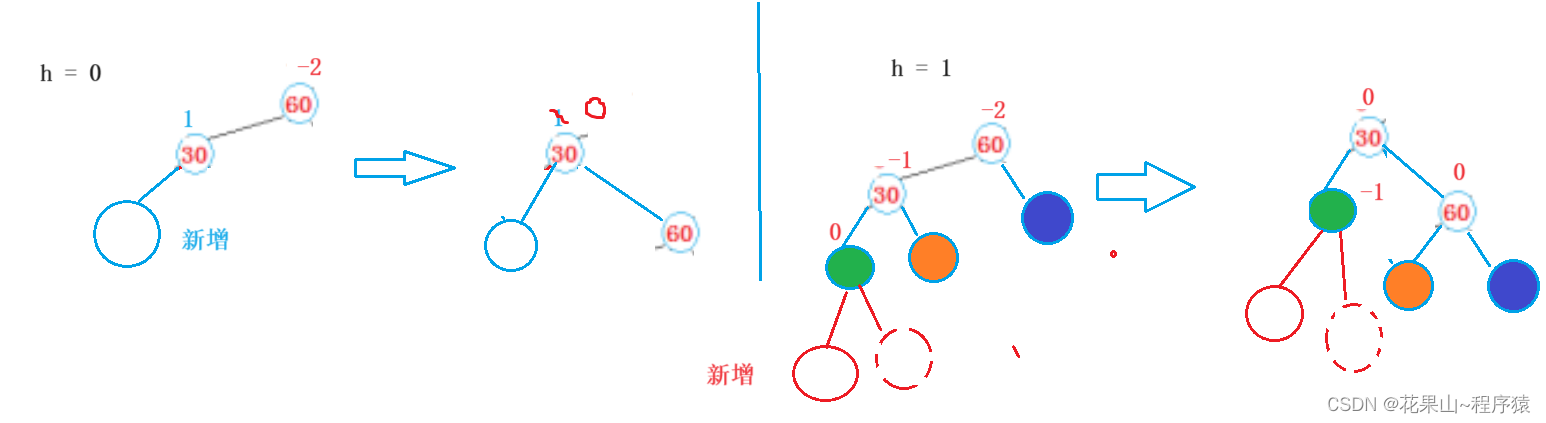
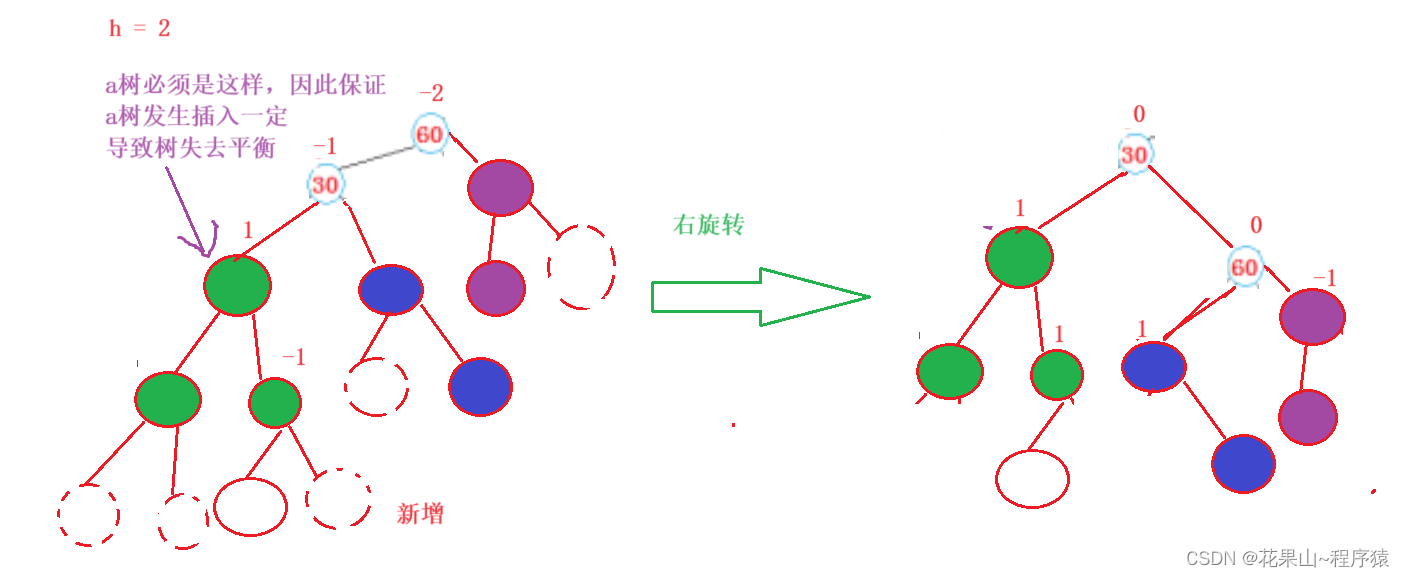
学会了法一自然会了法二:
void RotateR(AVL_Data* parent){assert(parent->left);AVL_Data* par = parent;AVL_Data* par_L = par->left;AVL_Data* par_LR = par->left->right;AVL_Data* ppnode = par->parent;par->left = par_LR;if (par_LR)par_LR->parent = par;par_L->right = par;par->parent = par_L;par_L->parent = ppnode;if (!ppnode){root = par_L;}else if (ppnode->left == par){ppnode->left = par_L;}else{ppnode->right = par_L;}par->_bf = 0;par_L->_bf = 0;}法三:先左后右双旋法
跟单旋一样,我们首先展示,当h = 0,1,2时需要左右双旋处理的场景。
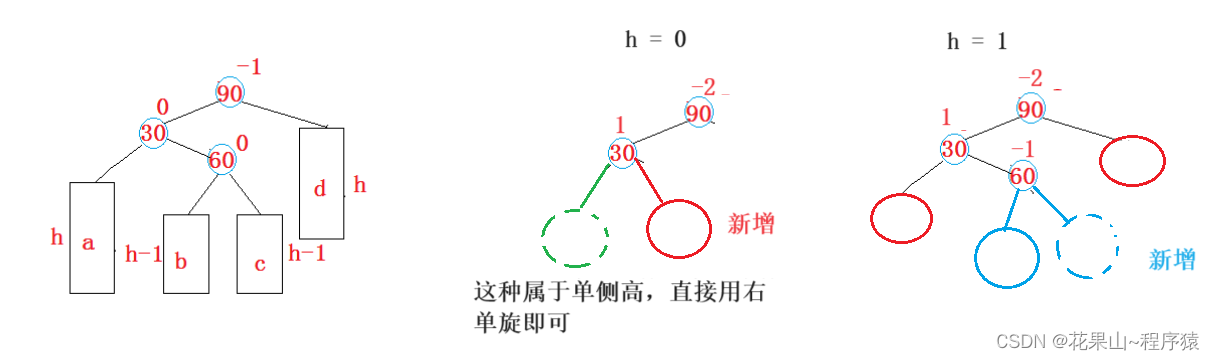
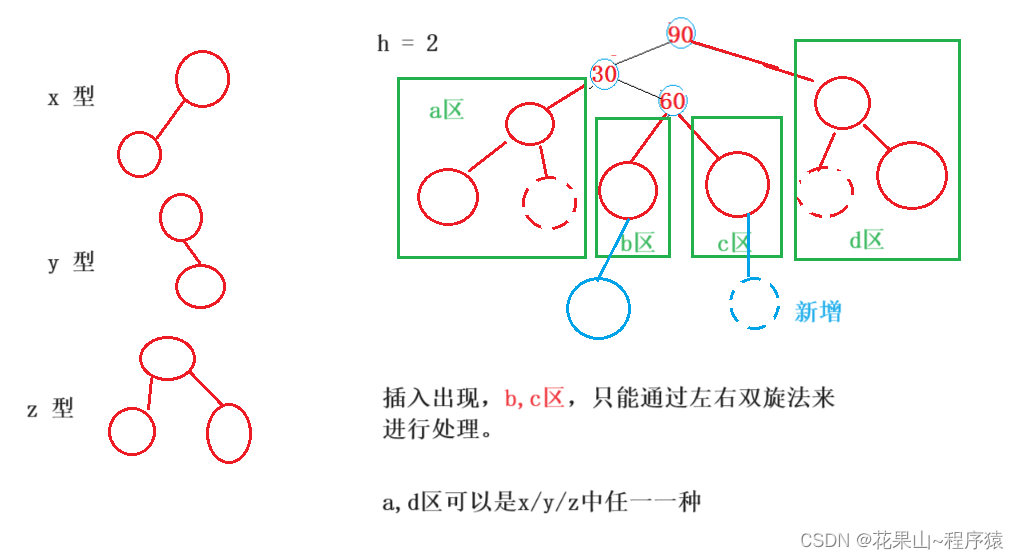
双旋法步骤变化流程,如下:

从结果来看,就是将60这个位置推上去置于“根”。
代码如下:
void RotateLR(AVL_Data* parent){assert(parent->left);AVL_Data* par = parent;AVL_Data* par_L = par->left;AVL_Data* par_LR = par->left->right;AVL_Data* ppnode = par->parent;int par_LR_bf = par_LR->_bf;RotateL(par_L);RotateR(par);if (par_LR_bf == -1){par->_bf = 1;par_L->_bf = 0;}else if (par_LR_bf == 1){par->_bf = 0;par_L->_bf = -1;}else if (par_LR_bf == 0){par->_bf = 0;par_L->_bf = 0;}else{assert(false);}par_LR->_bf = 0;}// 测试案例
void Test_insert_L()
{AVL_Tree<int, string> tree;tree.insert(make_pair(90, "李四"));tree.insert(make_pair(30, "二麻子"));tree.insert(make_pair(100, "张三"));tree.insert(make_pair(25, "王五"));tree.insert(make_pair(60, "王五"));tree.insert(make_pair(50, "王五"));
}法四:先右后左双旋法
我们学会法三后,照葫芦画瓢即可。
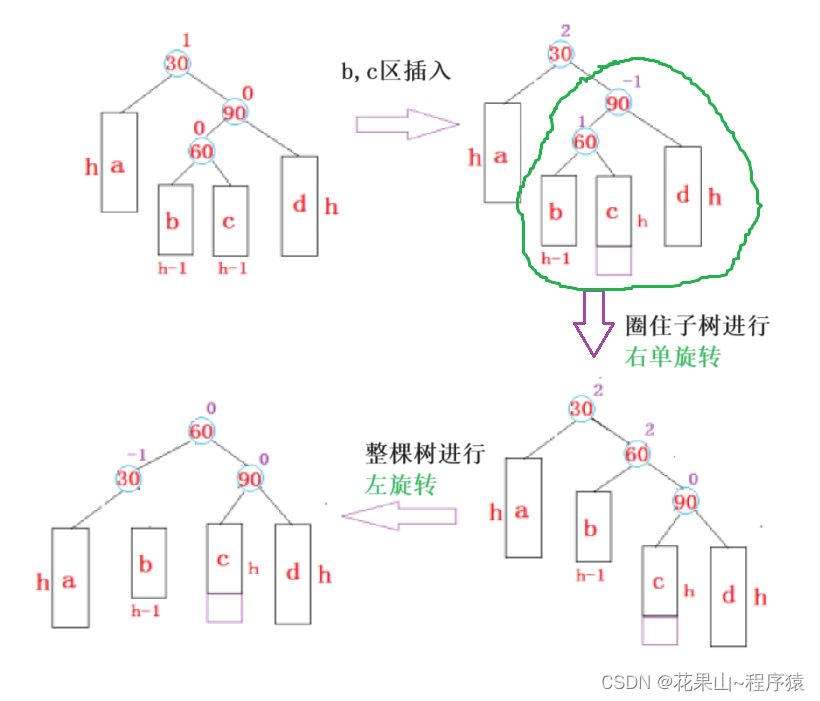
各场景:

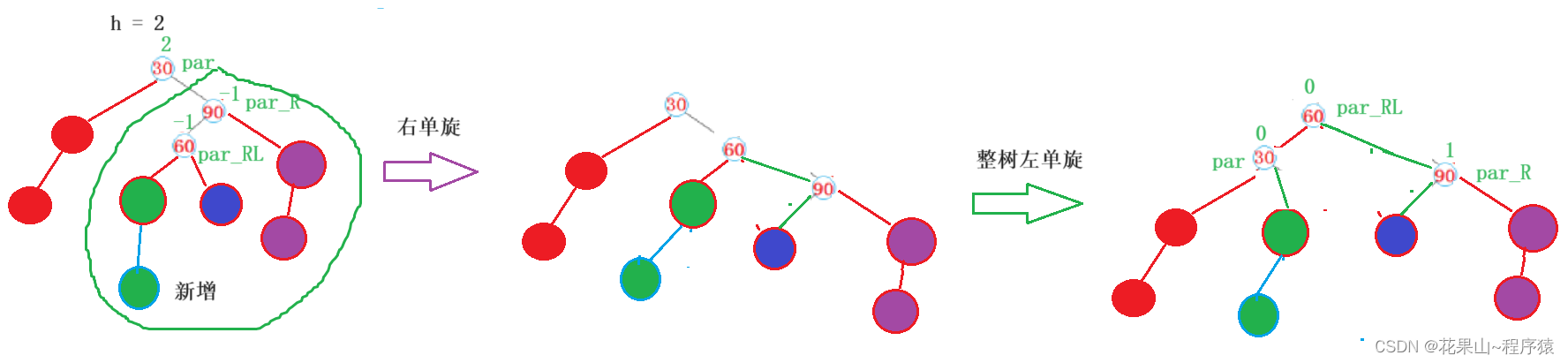
代码:
void RotateRL(AVL_Data* parent){assert(parent->right);AVL_Data* par = parent;AVL_Data* par_R = par->right;AVL_Data* par_RL = par->right->left;AVL_Data* ppnode = par->parent;int par_RL_bf = par_RL->_bf;RotateR(par_R);RotateL(par);if (par_RL_bf == -1){par->_bf = 0;par_R->_bf = 1;}else if (par_RL_bf == 1){par->_bf = -1;par_R->_bf = 0;}else if (par_RL_bf == 0){par->_bf = 0;par_R->_bf = 0;}else{assert(false);}par_RL->_bf = 0;}// 测试案例
void Test_insert_L()
{AVL_Tree<int, string> tree;tree.insert(make_pair(30, "李四"));tree.insert(make_pair(20, "二麻子"));tree.insert(make_pair(90, "张三"));tree.insert(make_pair(15, "王五"));tree.insert(make_pair(60, "王五"));tree.insert(make_pair(100, "王五"));tree.insert(make_pair(55, "王五"));tree.insert(make_pair(67, "王五"));tree.insert(make_pair(95, "王五"));tree.insert(make_pair(50, "王五"));
}测试(判断一棵树是否是AVL树)
思路:
1. 检查高度(AVL中每棵子树都是AVL树)。
2. 检查平衡因子是否正确。
代码如下:
int Hight(const AVL_Data* root){if (root == nullptr)return 0;int left_H = Hight(root->left);int left_R = Hight(root->right);return left_H >= left_R ? left_H + 1 : left_R + 1;}bool B_balance(){return _B_balance(root);}bool _B_balance(const AVL_Data* root){if (root == nullptr)return true;int left_root = Hight(root->left);int right_root = Hight(root->right);if ((right_root - left_root) != root->_bf) // 利用Hight,进行平衡因子判断return false; return abs(left_root - right_root) < 2 && _B_balance(root->left) && _B_balance(root->right);}3. 随机值案例
用这个代码多跑几次,差不多能遍历所有环境。
void Random_Test()
{srand(time(0));const size_t N = 10000000;AVL_Tree<int, int> t;for (size_t i = 0; i < N; i++){size_t x = rand();t.insert(make_pair(x, x));}cout << t.B_balance() << endl;
}快来测试自己的代码吧
insert全代码
bool insert(const pair<K, V>& p){AVL_Data* new_a_d = new AVL_Data(p);if (!root){root = new_a_d;}else{AVL_Data* cur = root;AVL_Data* parent = nullptr;while (cur){if (p.first < cur->_kv.first){parent = cur;cur = cur->left;}else if (p.first > cur->_kv.first){parent = cur;cur = cur->right;}else{delete(new_a_d); // 插入失败,删除新建结点return false;}}if (p.first < parent->_kv.first){parent->left = new_a_d;}else{parent->right = new_a_d;}new_a_d->parent = parent;cur = new_a_d;//完成插入,进行平衡while (parent){ // 插入,修改parent平衡因子if (cur == parent->right){parent->_bf++;}else{parent->_bf--;}// 判断parent平衡因子是否是0,如果非0则需要向祖先更新平衡因子if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->parent; }else if (parent->_bf == 0){break;}else if (parent->_bf == -2 || parent->_bf == 2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);// cout << "RotateL" << endl;}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);// cout << "RotateR" << endl;}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);// cout << "RotateLR" << endl;}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);// cout << "RotateRL" << endl;}else{// 出现其他情况,在插入时这棵AVL树本身就是异常AVL树// 问题出现在旋转方法assert(false);}break;}else{assert(false);}}return true;}}四,删除
下期预告: 红黑树!!!
结语
本小节就到这里了,感谢小伙伴的浏览,如果有什么建议,欢迎在评论区评论,如果给小伙伴带来一些收获请留下你的小赞,你的点赞和关注将会成为博主创作的动力。
相关文章:

保姆级认识AVL树【C++】(精讲:AVL Insert)
目录 前言 一,概念 二,定义 三,insert 1. 插入情况 情况一: 情况二: 情况三: 2. 旋转方法 法一:左单旋法 法二:右单旋法 法三:先左后右双旋法 法四…...
)
pinia中使用reactive声明变量,子页面使用时,值未改变,即不是响应式的(解决方法)
reactive赋值无效!reactive 不要直接data赋值!!!会丢失响应式的,只能通过obj.属性 属性值赋值 方法一. pinia中直接使用ref定义变量即可 export const useUserStoredefineStore(user,()>{let loginUserreactive({…...
基于springboot零食商城管理系统
功能如图所示 摘要 这基于Spring Boot的零食商城管理系统提供了强大的购物车和订单管理功能。用户可以在系统中浏览零食产品,并将它们添加到购物车中。购物车可以保存用户的选购商品,允许随时查看已选择的商品和它们的数量。一旦用户满意,他们…...

C++程序练习
定义一个类CheckPath,它由两个public方法组成: 1) checkPath:检查传入的字符串指定的路径是否存在,存在返回true,否则返回false。 2) createFilePath:根据传入的字符串指定的路径&…...

Golang 继承
在面向对象的编程语言中,继承是一种重要的机制,它允许子类继承父类的属性和方法。然而,Go语言在设计时没有直接支持传统意义上的继承,而是提供了一种更为灵活和简洁的方式来实现类似的功能。本文将探讨Golang中实现继承的方法和最…...
)
棋盘格测距-单目相机(OpenCV/C++)
一、文章内容简述: 1’ 通过cv::findChessboardCorners寻找棋盘格角点 2‘ 用cv::solvePnP计算旋转向量rvec和平移向量tvec 3’ 通过公式计算相机到棋盘格的距离 float distance sqrt(tvec.at<double>(0,0) * tvec.at<double>(0,0) tvec.at<do…...
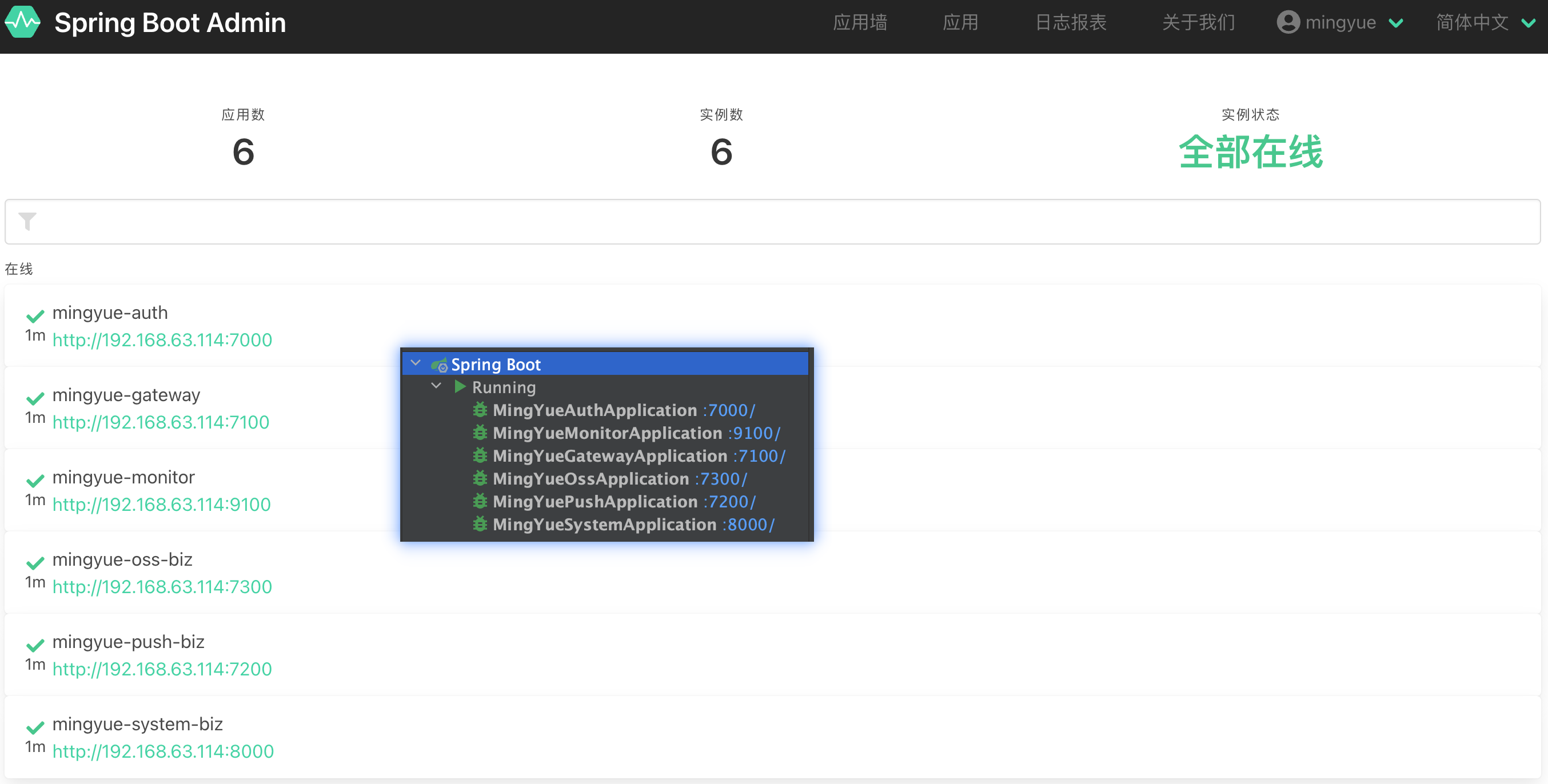
031-从零搭建微服务-监控中心(一)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址(后端):mingyue: 🎉 基于 Spring Boot、Spring Cloud & Alibaba 的分布式微服务架构基础服务中心 源…...
vue中使用xlsx插件导出多sheet excel实现方法
安装xlsx,一定要注意版本: npm i xlsx0.17.0 -S package.json: {"name": "hello-world","version": "0.1.0","private": true,"scripts": {"serve": "vue-c…...
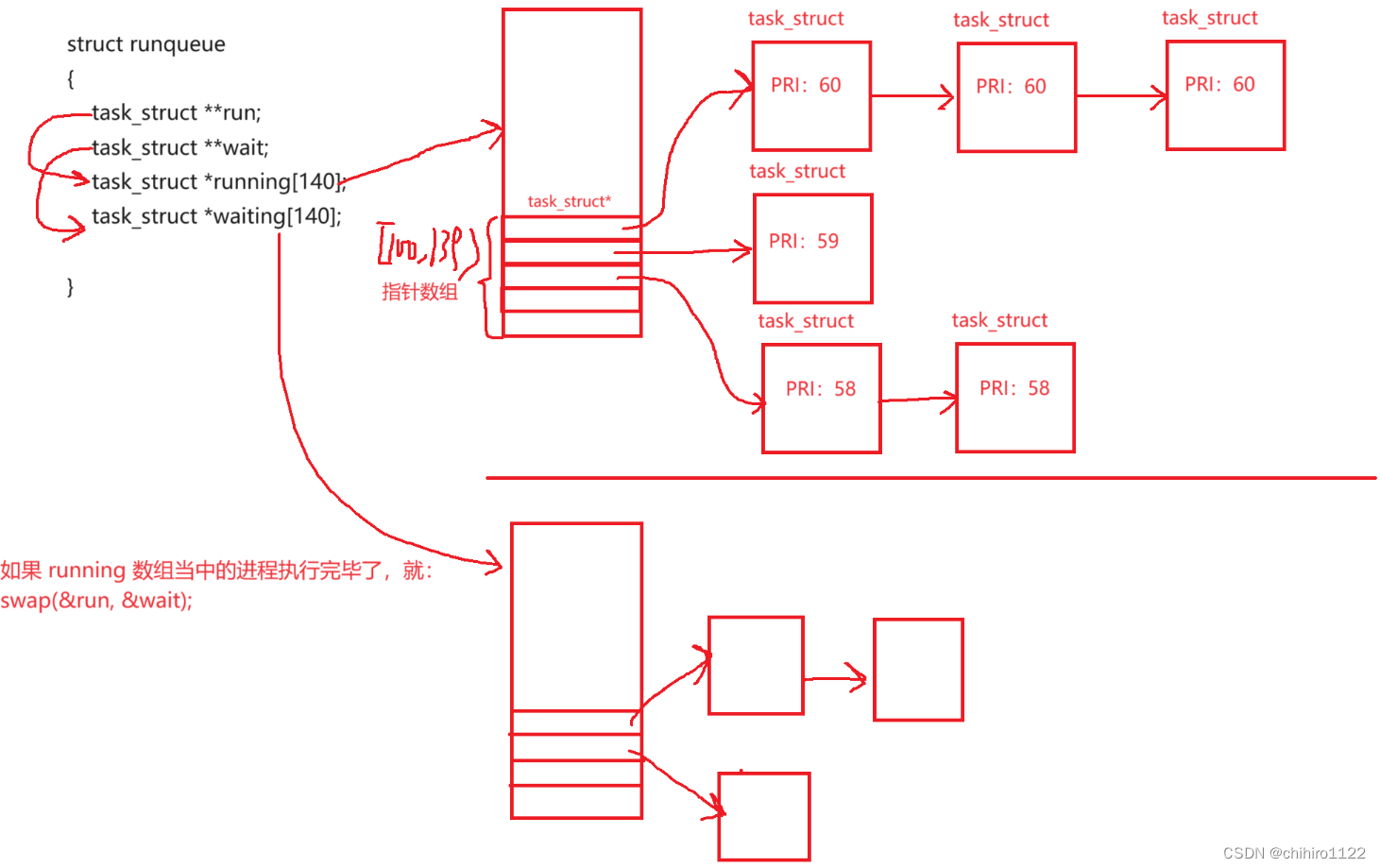
Linux - 进程的优先级 和 如何使用优先级调度进程
理解linux 当中如何做到 把一个PCB 放到多个 数据结构当中 在Linux 当中,一个进程的 PCB 不会仅仅值存在一个 数据结构当中,他既可以在 某一个队列当中,又可以在 一个 多叉树当中。 队列比如 cpu 的 运行队列,键盘的阻塞队列等等…...

支持控件drag和click
在 MouseDown 事件触发 DoDragDrop 拖拽操作时,Click 事件通常无效,因为 DoDragDrop 方法会捕获鼠标事件并等待拖拽操作完成。 有一个简单地思路解决这个问题 当MouseDow时,触发定时器,延迟100s定时器到时后,进入dra…...
AIR101 LuatOS LVGL 显示多个标签例程
屏幕资料 AIR101与屏幕连接 PC端仿真环境合宙官方PC端版本环境搭建教程 PC电脑仿真 -- sys库是标配 _G.sys require("sys") sys.taskInit(function()local cnt0lvgl.init(480,320)--lvgl初始化local cont lvgl.cont_create(nil, nil);-- lvgl.cont_set_fit(cont, …...
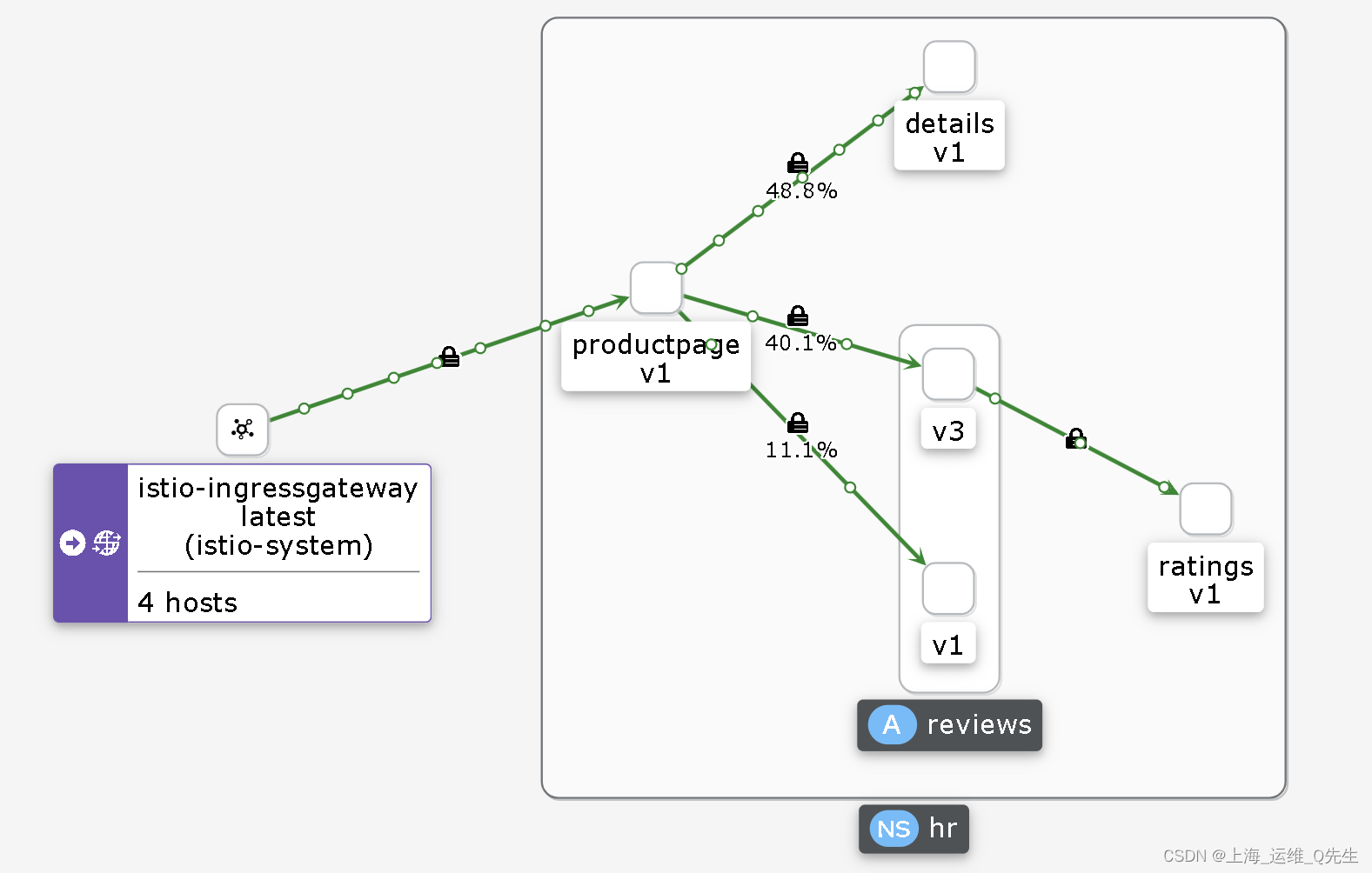
Istio实战(七)- Bookinfo 部署
1. Istio Bookinfo示例 1.1 部署Bookinfo # kubectl apply -f /apps/istio/samples/bookinfo/platform/kube/bookinfo.yaml -n hr1.2 确认Bookinfo已经部署正常 先确认以下pod和service已经被正确创建 # kubectl get pods -n hr NAME READY …...
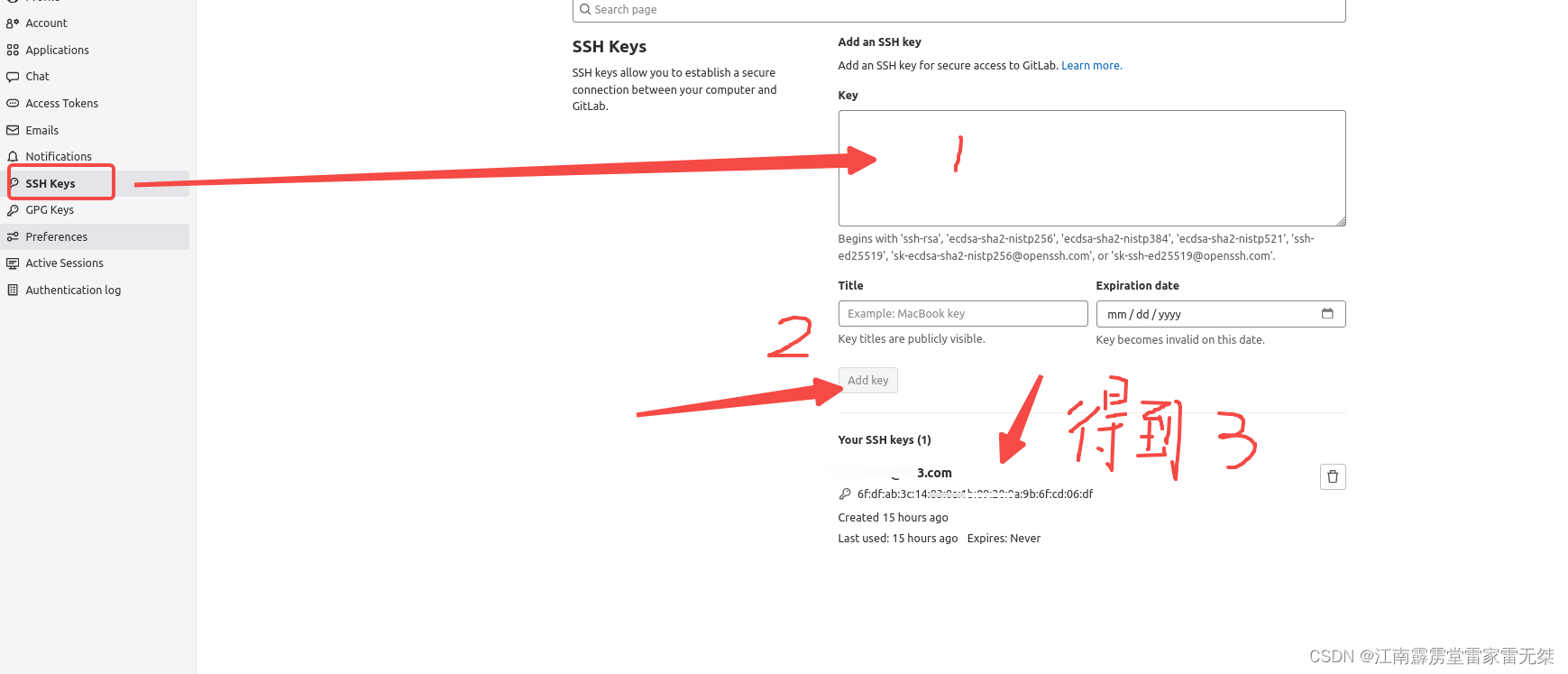
出差学小白知识No5:|Ubuntu上关联GitLab账号并下载项目(ssh key配置)
1 注冊自己的gitlab账户 有手就行 2 ubuntu安装git ,并查看版本 sudo apt-get install git git --version 3 vim ~/.ssh/config Host gitlab.example.com User your_username Port 22 IdentityFile ~/.ssh/id_rsa PreferredAuthentications publickey 替换gitl…...
FL Studio21.2中文版多少钱?值得下载吗
水果,全称Fruity Loop Studio,简称FL Studio。是一款全能的音乐制作软件,经过二十多年的演化更迭,其各项功能非常的先进。其开创性的Pat\song模式,也为初学者的学习提供了便利。那么水果音乐制作软件需要多少钱呢&…...
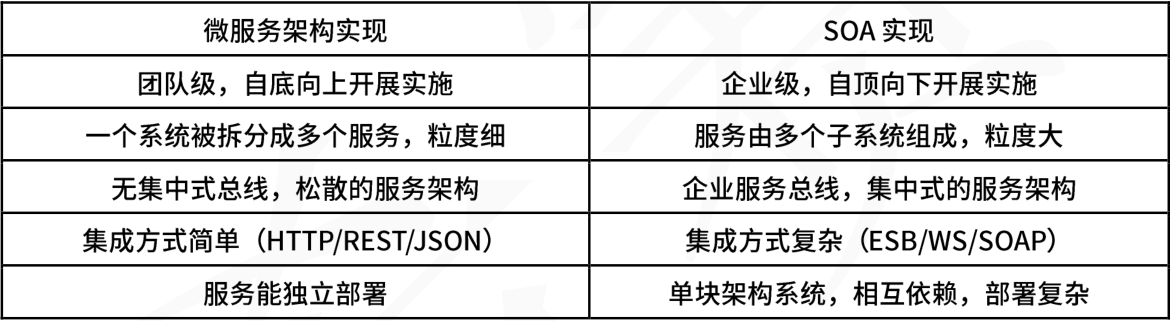
软考系统架构师知识点集锦三:软件架构设计
一、考情分析 二、考点精讲 2.1软件架构的概念 2.1.1什么是架构(暂无定论) 架构设计就是需求分配,即将满足需求的职责分配到组件上。 软件架构风格是描述某-特定应用领域中系统组织方式的惯用模式。架构风格定义-个系统家族,即一个体系结构定义一个词汇表和一组约…...
docker - window Docker Desktop升级
文章目录 前言docker - window Docker Desktop升级 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每天的运气都不会太差,实在白嫖的话,那欢迎常来…...
Element UI + Vue 新增和编辑共用表单校验无法清除问题(已解决)
问题描述 在新增和编辑过程中大部分情况下 两个表单是一致的,而且编辑也有回显需要,所有绝大多数情况下 都是一个表单两个用处,但是随之而来出现了一个无法清除校验的问题,在先点击编辑后再点击新增会出现校验红字: …...
FL Studio21最新中文汉化解锁版,2024怎么激活FL Studio
FL Studio2024最新中文汉化解锁版是一款功能强大的数字音频工作站(DAW),它广泛应用于音乐创作和音乐制作领域。在使用FL Studio时,购买正版软件是否有必要呢?本文将详细探讨FL Studio的功能特点以及正版软件的重要性。…...
Mac怎么清理磁盘空间?释放Mac磁盘空间有效方法
相信很多使用macOS系统的小伙伴都收到过提示“磁盘空间已满”消息,尤其是采用SSD固态硬盘的MacBook系列,120G的硬盘空间本就捉襟见肘,使用一段时间后,即使自己没有存放很多大文件, Mac的磁盘很快就满了。那么ÿ…...
城市干道分段绿波协调控制模型研究)
论文阅读(一)城市干道分段绿波协调控制模型研究
[1]酆磊,赵欣,李林等.城市干道分段绿波协调控制模型研究[J].武汉理工大学学报(交通科学与工程版),2021,45(06):1034-1038. 主要内容:该文介绍了基于绿波带宽和关联度的城市干道分段绿波协调控制模型。通过将主干道划分为不同子区域,并根据路段特点进行精准化控制,实现了分段…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
