《动手学深度学习 Pytorch版》 10.6 自注意力和位置编码
在注意力机制中,每个查询都会关注所有的键-值对并生成一个注意力输出。由于查询、键和值来自同一组输入,因此被称为 自注意力(self-attention),也被称为内部注意力(intra-attention)。本节将使用自注意力进行序列编码,以及使用序列的顺序作为补充信息。
import math
import torch
from torch import nn
from d2l import torch as d2l
10.6.1 自注意力

给定一个由词元组成的输入序列 x 1 , … , x n \boldsymbol{x}_1,\dots,\boldsymbol{x}_n x1,…,xn,其中任意 x i ∈ R d ( 1 ≤ i ≤ n ) \boldsymbol{x}_i\in\R^d\quad(1\le i\le n) xi∈Rd(1≤i≤n) 。该序列的自注意力输出为一个长度相同的序列 y 1 , … , y n \boldsymbol{y}_1,\dots,\boldsymbol{y}_n y1,…,yn,其中:
y i = f ( x i , ( x 1 , x 1 ) , … , ( x n , x n ) ) ∈ R d \boldsymbol{y}_i=f(\boldsymbol{x}_i,(\boldsymbol{x}_1,\boldsymbol{x}_1),\dots,(\boldsymbol{x}_n,\boldsymbol{x}_n))\in\R^d yi=f(xi,(x1,x1),…,(xn,xn))∈Rd
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens, # 基于多头注意力对一个张量完成自注意力的计算num_hiddens, num_heads, 0.5)
attention.eval()
MultiHeadAttention((attention): DotProductAttention((dropout): Dropout(p=0.5, inplace=False))(W_q): Linear(in_features=100, out_features=100, bias=False)(W_k): Linear(in_features=100, out_features=100, bias=False)(W_v): Linear(in_features=100, out_features=100, bias=False)(W_o): Linear(in_features=100, out_features=100, bias=False)
)
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens)) # 张量的形状为(批量大小,时间步的数目或词元序列的长度,d)。
attention(X, X, X, valid_lens).shape # 输出与输入的张量形状相同
torch.Size([2, 4, 100])
10.6.2 比较卷积神经网络、循环神经网络和自注意力

-
卷积神经网络
-
计算复杂度为 O ( k n d 2 ) O(knd^2) O(knd2)
-
k k k 为卷积核大小
-
n n n 为序列长度是
-
d d d 为输入和输出的通道数量
-
-
并行度为 O ( n ) O(n) O(n)
-
最大路径长度为 O ( n / k ) O(n/k) O(n/k)
-
-
循环神经网络
-
计算复杂度为 O ( n d 2 ) O(nd^2) O(nd2)
d × d d\times d d×d 权重矩阵和 d d d 维隐状态的乘法计算复杂度为 O ( d 2 ) O(d^2) O(d2),由于序列长度为 n n n,因此循环神经网络层的计算复杂度为 O ( n d 2 ) O(nd^2) O(nd2)
-
并行度为 O ( 1 ) O(1) O(1)
有 O ( n ) O(n) O(n) 个顺序操作无法并行化。
-
最大路径长度也是 O ( n ) O(n) O(n)
-
-
自注意力
-
计算复杂度为 O ( n 2 d ) O(n^2d) O(n2d)
查询、键和值都是 n × d n\times d n×d 矩阵
-
并行度为 O ( n ) O(n) O(n)
每个词元都通过自注意力直接连接到任何其他词元。因此有 O ( 1 ) O(1) O(1) 个顺序操作可以并行计算
-
最大路径长度也是 O ( 1 ) O(1) O(1)
-
总而言之,卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
10.6.3 位置编码
在处理词元序列时,循环神经网络是逐个的重复地处理词元的,而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息,通过在输入表示中添加 位置编码(positional encoding) 来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。
基于正弦函数和余弦函数的固定位置编码的矩阵第 i i i 行、第 2 j 2j 2j 列和 2 j + 1 2j+1 2j+1 列上的元素为:
p i , 2 j = sin ( i 1000 0 2 j / d ) p i , 2 j + 1 = cos ( i 1000 0 2 j / d ) \begin{align} p_{i,2j}&=\sin{\left(\frac{i}{10000^{2j/d}}\right)}\\ p_{i,2j+1}&=\cos{\left(\frac{i}{10000^{2j/d}}\right)} \end{align} pi,2jpi,2j+1=sin(100002j/di)=cos(100002j/di)
#@save
class PositionalEncoding(nn.Module):"""位置编码"""def __init__(self, num_hiddens, dropout, max_len=1000):super(PositionalEncoding, self).__init__()self.dropout = nn.Dropout(dropout)# 创建一个足够长的Pself.P = torch.zeros((1, max_len, num_hiddens))X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) / torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)self.P[:, :, 0::2] = torch.sin(X)self.P[:, :, 1::2] = torch.cos(X)def forward(self, X):X = X + self.P[:, :X.shape[1], :].to(X.device)return self.dropout(X)
在位置嵌入矩阵 P \boldsymbol{P} P 中,行代表词元在序列中的位置,列代表位置编码的不同维度。从下面的例子中可以看到位置嵌入矩阵的第 6 列和第 7 列的频率高于第 8 列和第 9 列。第 6 列和第 7 列之间的偏移量(第 8 列和第 9 列相同)是由于正弦函数和余弦函数的交替。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])

10.6.3.1 绝对位置信息
打印出 0 , 1 , … , 7 0,1,\dots,7 0,1,…,7 的二进制表示形式即可明白沿着编码维度单调降低的频率与绝对位置信息的关系。
每个数字、每两个数字和每四个数字上的比特值在第一个最低位、第二个最低位和第三个最低位上分别交替。
for i in range(8):print(f'{i}的二进制是:{i:>03b}')
0的二进制是:000
1的二进制是:001
2的二进制是:010
3的二进制是:011
4的二进制是:100
5的二进制是:101
6的二进制是:110
7的二进制是:111
在二进制表示中,较高比特位的交替频率低于较低比特位,与下面的热图所示相似,只是位置编码通过使用三角函数在编码维度上降低频率。由于输出是浮点数,因此此类连续表示比二进制表示法更节省空间。
P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

10.6.3.2 相对位置信息
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移 δ \delta δ,位置 i + δ i+\delta i+δ 处的位置编码可以线性投影位置 i i i 处的位置编码来表示。
这种投影的数学解释是,令 ω j = 1 / 1000 0 2 j / d \omega_j=1/10000^{2j/d} ωj=1/100002j/d,对于任何确定的位置偏移 δ \delta δ,上个式子中的任何一对 ( p i , 2 j , p i , 2 j + 1 ) (p_{i,2j},p_{i,2j+1}) (pi,2j,pi,2j+1) 都可以线性投影到 ( p i + δ , 2 j , p i + δ , 2 j + 1 ) (p_{i+\delta,2j},p_{i+\delta,2j+1}) (pi+δ,2j,pi+δ,2j+1):
[ cos ( δ ω j ) sin ( δ ω j ) − sin ( δ ω j ) cos ( δ ω j ) ] [ p i , 2 j p i , 2 j + 1 ] = [ cos ( δ ω j ) sin ( i ω j ) + sin ( δ ω j ) cos ( i ω j ) − sin ( δ ω j ) sin ( i ω j ) + cos ( δ ω j ) cos ( i ω j ) ] = [ sin ( ( i + δ ) ω j ) cos ( ( i + δ ) ω j ) ] = [ p i , 2 j p i , 2 j + 1 ] \begin{align} &\begin{bmatrix} \cos{(\delta\omega_j)} & \sin{(\delta\omega_j)}\\ -\sin{(\delta\omega_j)} & \cos{(\delta\omega_j)} \end{bmatrix} \begin{bmatrix} p_{i,2j}\\ p_{i,2j+1} \end{bmatrix}\\ =&\begin{bmatrix} \cos{(\delta\omega_j)}\sin{(i\omega_j)}+\sin{(\delta\omega_j)}\cos{(i\omega_j)}\\ -\sin{(\delta\omega_j)}\sin{(i\omega_j)}+\cos{(\delta\omega_j)}\cos{(i\omega_j)} \end{bmatrix}\\ =&\begin{bmatrix} \sin{((i+\delta)\omega_j)}\\ \cos{((i+\delta)\omega_j)} \end{bmatrix}\\ =&\begin{bmatrix} p_{i,2j}\\ p_{i,2j+1} \end{bmatrix} \end{align} ===[cos(δωj)−sin(δωj)sin(δωj)cos(δωj)][pi,2jpi,2j+1][cos(δωj)sin(iωj)+sin(δωj)cos(iωj)−sin(δωj)sin(iωj)+cos(δωj)cos(iωj)][sin((i+δ)ωj)cos((i+δ)ωj)][pi,2jpi,2j+1]
2 × 2 2\times 2 2×2 投影矩阵不依赖于任何位置的索引 i i i。
练习
(1)假设设计一个深度架构,通过堆叠基于位置编码的自注意力层来表示序列。可能会存在什么问题?
(2)请设计一种可学习的位置编码方法。
相关文章:

《动手学深度学习 Pytorch版》 10.6 自注意力和位置编码
在注意力机制中,每个查询都会关注所有的键-值对并生成一个注意力输出。由于查询、键和值来自同一组输入,因此被称为 自注意力(self-attention),也被称为内部注意力(intra-attention)…...

2023年第四届MathorCup高校数学建模挑战赛——大数据竞赛B题 实现代码
根据之前发布的思路 第一步 进行数据合并 import pandas as pd# 读取所有附件的数据 data1 pd.read_excel(附件一.xlsx) data2 pd.read_excel(附件二.xlsx) data3 pd.read_excel(附件三.xlsx) data4 pd.read_excel(附件四.xlsx)# 根据商品编码将附件一和附件二连接 combi…...

larvel 中的api.php_Laravel 开发 API
Laravel10中提示了Target *classController does not exist,为什么呢? 原因是:laravel8开始写法变了。换成了新的写法了 解决方法一: 在路由数组加入App\Http\Controllers\即可。 <?phpuse Illuminate\Support\Facades\Route;…...

虚拟机构建部署单体项目及前后端分离项目
目录 一.部署单体项目 1.远程数据库 1.1远程连接数据库 1.2 新建数据库运行sql文件 2.部署项目到服务器中 3.启动服务器运行 二.部署前后端分离项目 1.远程数据库和部署到服务器 2.利用node环境启动前端项目 3.解决主机无法解析服务器localhost问题 方法一 编辑 方法二 一.部…...
C++之特殊类的设计
目录 一、单例模式 1、设计模式 2、单例模式 1、饿汉模式 2、懒汉模式 3、单例对象的释放问题 二、设计一个不能被拷贝的类 三、设计一个只能在堆上创建对象的类 四、设计一个只能在栈上创建对象的类 五、设计一个不能被继承的类 一、单例模式 1、设计模式 概念&am…...
Java练习题2020 -1
统计1到N的整数中,被A除余A-1的偶数的个数 输入说明:整数 N(N<10000), A, (A 输出说明:符合条件的数的个数 输入样例:10 3 输出样例:2 (说明:样例中符合条件的2个数是 2、8) import java.util.Scanner;p…...

LuaTable转C#的列表List和字典Dictionary
LuaTable转C#的列表List和字典Dictionaty 介绍lua中创建表测试lua中list表表转成List表转成Dictionary 键值对表表转成Dictionary 多类型键值对表表转成Dictionary 总结 介绍 之前基本都是从C#中的List或者Dictionary转成luaTable,很少会把LuaTable转成C#的List或者…...
)
Redis快速上手篇七(集群)
在赶工了..... Redis集群 主从复制的场景无法吗满足主机单点故障时需要引入集群配置 一般数据库要处理的读请求远大于写请求 ,针对这种情况,我们优化数据库可以采用读写分离的策略。我们可以部 署一台主服务器主要用来处理写请求,部署多台从…...
Mac 安装nvm
安装方案: 1. 从github下载nvm仓库到 ~/目录 地址:https://github.com/nvm-sh/nvm.git git clone https://github.com/nvm-sh/nvm.git 2. 进入nvm目录中执行install.sh等待执行完成,执行的操作方法就是直接将文件拖入到终端然后回车。 3.…...

python 从mssql取出datetime2类型之后格式化
我mssql是datetime2类型,用df取出之后发现是个纳秒的int(1698419713000000000 这种) 所以格式化的话就需要变成秒为单位,他们之间是10的9次方倍。所以先除以1e9之后用datetime.datetime.fromtimestamp()转换之后再format就行了 l…...
18.2 使用NPCAP库抓取数据包
NPCAP 库是一种用于在Windows平台上进行网络数据包捕获和分析的库。它是WinPcap库的一个分支,由Nmap开发团队开发,并在Nmap软件中使用。与WinPcap一样,NPCAP库提供了一些API,使开发人员可以轻松地在其应用程序中捕获和处理网络数据…...
pytest-yaml 测试平台-3.创建执行任务定时执行用例
前言 当项目用例编写完成后,需设置执行策略,可以用到定时任务设置每天几点执行。或者间隔几个小时执行一次。 创建定时任务 创建任务 勾选需要执行的项目以及运行环境 触发器可以支持2种方式:interval 间隔多久触发和 cron 表达式定时执行…...

安卓文件资源中,一个字串包含引用其他字串的写法
具体范例: <string name"product_name" translatable"false">Miscope</string><string name"app_name">string/product_name for USB Camera</string> 注意要先定义再引用。...

解决:谷歌浏览器访问http时,自动转https访问的问题
问题背景:某个系统网站,之前一直用https域名访问,现在改成http域名后,用http访问,谷歌浏览器会自动跳转到https。 解决方法: 在浏览器中输入网址:chrome://net-internals/#hsts -》 在“Delete…...
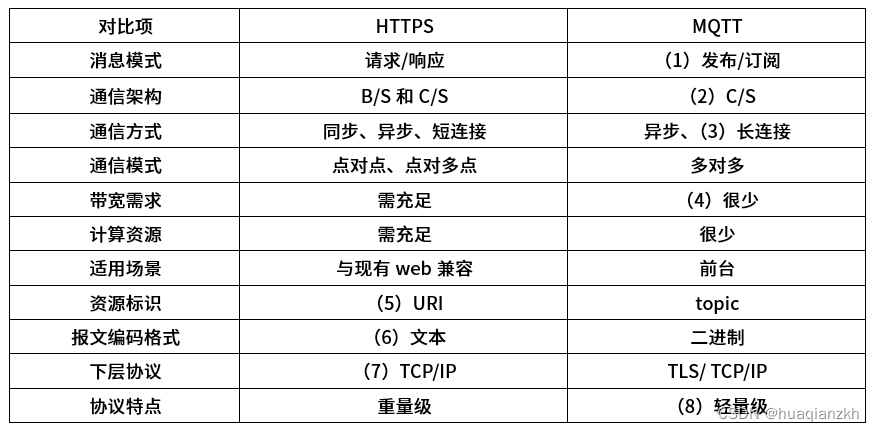
MQTT协议和边缘计算
1.基本概念 MQTT是基于TCP/IP协议栈构建的异步通信消息协议,是一种轻量级的发布、订阅信息传输协议。可以在不可靠的网络环境中进行扩展,适用于设备硬件存储空间或网络带宽有限的场景。使用MQTT协议,消息发送者与接收者不受时间和空间的限制…...
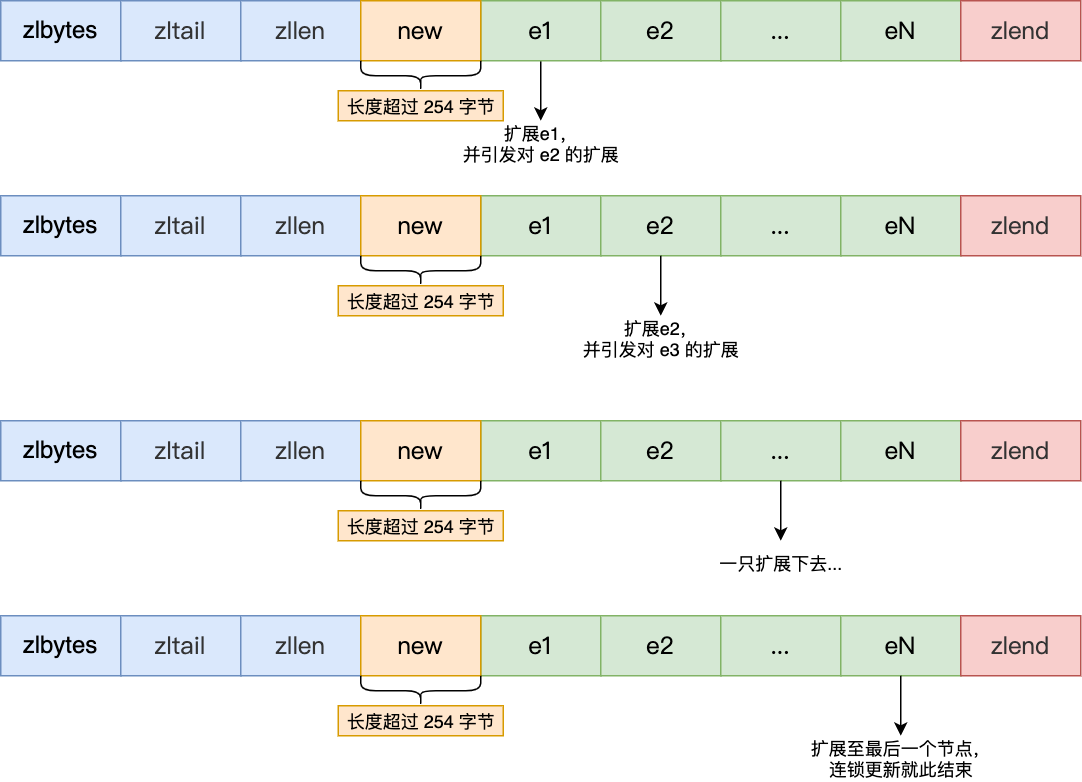
Redis(04)| 数据结构-压缩列表
压缩列表的最大特点,就是它被设计成一种内存紧凑型的数据结构,占用一块连续的内存空间,不仅可以利用 CPU 缓存,而且会针对不同长度的数据,进行相应编码,这种方法可以有效地节省内存开销。 但是,…...
(灵神笔记))
516 最长回文子序列(区间DP)(灵神笔记)
题目 最长回文子序列 给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。 子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。 示例 1: 输入:s …...
Kafka - 异步/同步发送API
文章目录 异步发送普通异步发送异步发送流程Code 带回调函数的异步发送带回调函数的异步发送流程Code 同步发送API 异步发送 普通异步发送 需求:创建Kafka生产者,采用异步的方式发送到Kafka broker 异步发送流程 Code <!-- https://mvnrepository…...

嵌套for循环在外层循环和内层循环中使用两个Executors.newCachedThreadPool缓存线程池执行操作
1. 首先,我们需要创建两个ExecutorService对象,这两个对象将作为我们的缓存线程池。 2. 然后,我们使用嵌套的for循环来执行我们的操作。在每个外层循环中,我们将创建一个新的任务并提交给外层线程池。在这个任务中,我…...
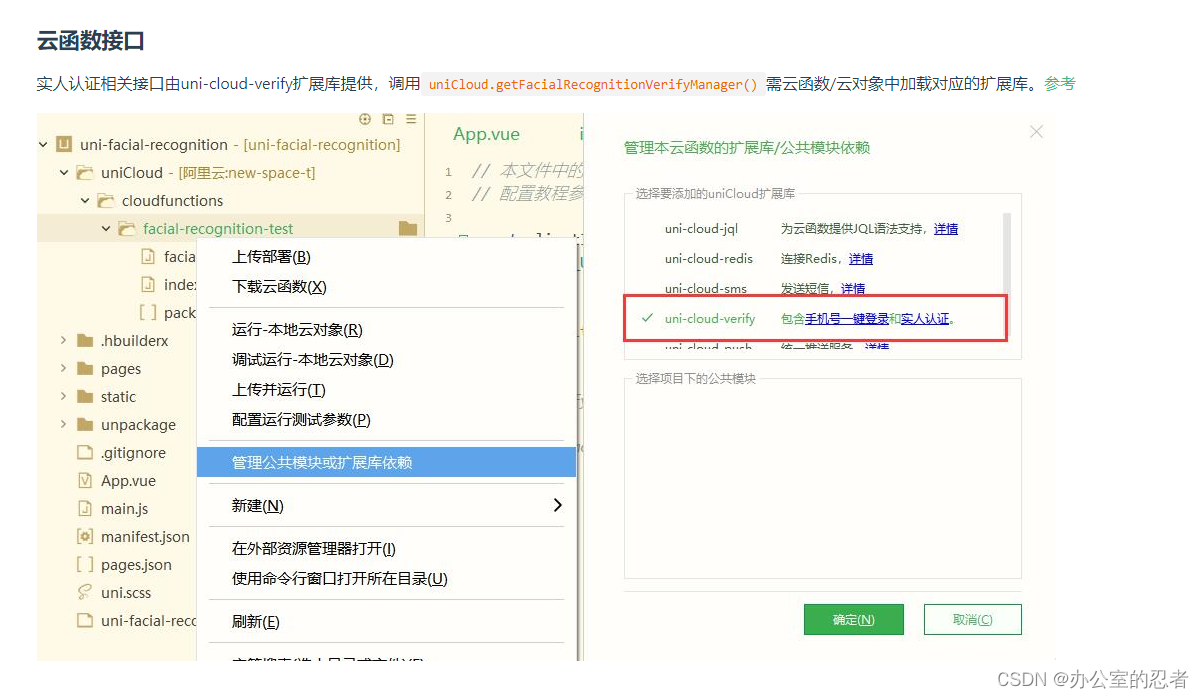
【uniapp+云函数调用】人脸识别,实人认证,适用于app,具体思路解析,已实现
2023.10.8 需求: uniapp开发的app项目中使用人脸识别 app项目都是第一次搞,更别提人脸识别了。目前已有的就是Dcloud账号已申请,实现需求的时间没那么紧迫 此篇会详细记录从0到1的过程 2023.10.24 今天开始探究实现的过程 可能会记录的有些冗余 效果图如下: uniapp开发指南…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
