Python 算法高级篇:归并排序的优化与外部排序
Python 算法高级篇:归并排序的优化与外部排序
- 引言
- 1. 归并排序的基本原理
- 2. 归并排序的优化
- 2.1 自底向上的归并排序
- 2.2 最后优化
- 3. 外部排序
- 4. 性能比较
- 5. 结论
引言
在计算机科学中,排序是一项基本的任务,而归并排序( Merge Sort )是一种著名的排序算法,它具有稳定性和良好的时间复杂度。本文将介绍归并排序的基本原理,然后深入探讨如何进行优化以及如何应用归并排序进行外部排序。
😃😄 ❤️ ❤️ ❤️
1. 归并排序的基本原理
归并排序采用分治的策略,将一个大问题分解为小问题,解决小问题,然后将它们合并以获得最终解决方案。其基本步骤如下:
- 1 . 分割( Divide ):将数组划分为两个子数组,通常是平均分割。
- 2 . 递归( Conquer ):递归地对子数组进行排序。
- 3 . 合并( Merge ):将排好序的子数组合并为一个有序的数组。
下面是一个简单的归并排序算法的 Python 实现:
def merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2 # 找到数组的中间位置left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half) # 递归排序左半部分merge_sort(right_half) # 递归排序右半部分i = j = k = 0# 合并两个子数组while i < len(left_half) and j < len(right_half):if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1
归并排序的时间复杂度是 O ( n log n ),它是一种稳定的排序算法,但它需要额外的空间来存储临时数组。
2. 归并排序的优化
尽管归并排序的时间复杂度相对较低,但它在实际应用中可能会因为空间复杂度较高而受到限制。为了解决这个问题,可以进行一些优化。
2.1 自底向上的归并排序
传统的归并排序是自顶向下的,即从顶部开始递归划分子数组。在自底向上的归并排序中,我们从底部开始,首先将相邻的元素两两合并,然后是四四合并,八八合并,直到整个数组排序完成。这样可以减少递归所需的栈空间,降低空间复杂度。
以下是自底向上归并排序的 Python 实现:
def merge_sort_bottom_up(arr):n = len(arr)curr_size = 1while curr_size < n:for left in range(0, n - 1, 2 * curr_size):mid = min(left + curr_size - 1, n - 1)right = min(left + 2 * curr_size - 1, n - 1)if mid < right:merge(arr, left, mid, right)curr_size *= 2def merge(arr, left, mid, right):n1 = mid - left + 1n2 = right - midL = [0] * n1R = [0] * n2for i in range(n1):L[i] = arr[left + i]for i in range(n2):R[i] = arr[mid + i + 1]i = j = 0k = leftwhile i < n1 and j < n2:if L[i] <= R[j]:arr[k] = L[i]i += 1else:arr[k] = R[j]j += 1k += 1while i < n1:arr[k] = L[i]i += 1k += 1while j < n2:arr[k] = R[j]j += 1k += 1
2.2 最后优化
归并排序的一个缺点是它需要额外的空间来存储临时数组。为了避免这种情况,可以使用一个额外的数组来存储一半的数据,然后交替地将数据复制到原始数组中。这可以降低空间复杂度,但增加了一些额外的复制操作。
以下是这种优化方法的 Python 实现:
def merge_sort_optimized(arr):n = len(arr)temp_arr = [0] * ncurr_size = 1while curr_size < n:left = 0while left < n - 1:mid = min(left + curr_size - 1, n - 1)right = min(left + 2 * curr_size - 1, n - 1)if mid < right:merge_optimized(arr, left, mid, right, temp_arr)left += 2 * curr_sizecurr_size *= 2def merge_optimized(arr, left, mid, right, temp_arr):i = leftj = mid + 1for k in range(left, right + 1):temp_arr[k] = arr[k]k = leftwhile i <= mid and j <= right:if temp_arr[i] <= temp_arr[j]:arr[k] = temp_arr[i]i += 1else:arr[k] = temp_arr[j]j += 1k += 1while i <= mid:arr[k] = temp_arr[i]k += 1i += 1
这种优化方法减少了内存的使用,但增加了一些额外的复制操作。
3. 外部排序
归并排序还可以应用于外部排序,这是一种处理大规模数据集的排序方法。外部排序的主要思想是将大数据集分成多个小数据块,每个小数据块都可以在内存中进行排序。排序后,将这些小数据块合并成一个有序的大数据集。
下面是一个简单的外部排序示例,假设我们有一个非常大的文件,无法一次性加载到内存中进行排序。我们可以将文件划分为多个小文件块,分别进行排序,然后合并它们。
def external_sort(input_file, output_file, chunk_size):# 划分文件为多个块divide_file(input_file, chunk_size)# 对每个块进行内部排序sort_chunks()# 合并排序后的块merge_sorted_chunks(output_file)def divide_file(input_file, chunk_size):# 从输入文件中读取数据并划分为块passdef sort_chunks():# 对每个块进行内部排序passdef merge_sorted_chunks(output_file):# 合并排序后的块pass
这个示例演示了如何将大文件划分为多个小文件块,每个块都可以在内存中排序。然后,排序后的块将被合并为一个有序的输出文件。
4. 性能比较
为了演示归并排序的不同优化版本之间的性能差异,我们可以使用一些基准测试来比较它们的运行时间。下面是一个简单的性能比较示例:
import random
import timeitarr = [random.randint(1, 1000) for _ in range(1000)]# 未优化的归并排序
def merge_sort_original(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort_original(left_half)merge_sort_original(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half):if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1# 测试未优化的归并排序的性能
original_time = timeit.timeit(lambda: merge_sort_original(arr.copy()), number=1000)# 优化的归并排序
def merge_sort_optimized(arr):# 同上,省略优化后的代码# 测试优化的归并排序的性能
optimized_time = timeit.timeit(lambda: merge_sort_optimized(arr.copy()), number=1000)print("未优化的归并排序耗时:", original_time)
print("优化的归并排序耗时:", optimized_time)
在上述示例中,我们对未优化的归并排序和优化后的归并排序进行了性能测试。通过这种方式,你可以比较它们的性能并选择最适合你应用的版本。
5. 结论
归并排序是一种经典的排序算法,它使用分治策略和合并操作,具有稳定的性质和较低的时间复杂度。通过进行优化,例如自底向上的归并排序和减少内存使用的外部排序,我们可以提高归并排序的性能和适用性。根据应用的需求和资源限制,选择合适的排序算法版本,以获得最佳性能。这些优化方法可以在处理大数据集和内存受限的情况下发挥重要作用。
[ 专栏推荐 ]
😃 《Python 算法初阶:入门篇》😄
❤️【简介】:本课程是针对 Python 初学者设计的算法基础入门课程,涵盖算法概念、时间复杂度、空间复杂度等基础知识。通过实例演示线性搜索、二分搜索等算法,并介绍哈希表、深度优先搜索、广度优先搜索等搜索算法。此课程将为学员提供扎实的 Python 编程基础与算法入门,为解决实际问题打下坚实基础。

相关文章:

Python 算法高级篇:归并排序的优化与外部排序
Python 算法高级篇:归并排序的优化与外部排序 引言 1. 归并排序的基本原理2. 归并排序的优化2.1 自底向上的归并排序2.2 最后优化 3. 外部排序4. 性能比较5. 结论 引言 在计算机科学中,排序是一项基本的任务,而归并排序( Merge S…...

LeetCode--1991.找到数组的中间位置
1 题目描述 给你一个下标从 0 开始的整数数组 nums , 请你找到 最左边 的中间位置 middleIndex (也就是所有可能中间位置下标最小的一个) 中间位置 middleIndex 是满足 nums[0] nums[1] ... nums[middleIndex-1] nums[middleIndex1] nums[middleI…...

物联网数据采集网关连接设备与云平台的关键桥梁
随着工业4.0和智能制造的快速发展,物联网数据采集网关在工业物联网中的应用越来越广泛。物联网数据采集网关作为连接设备与云端之间的关键桥梁,能够实现高效、可靠、安全的数据传输和转换,为智能制造和工业4.0提供了强大的支持。 一、物联网…...

专家级数据恢复:UFS Explorer Professional Recovery Crack
UFS Explorer Professional Recovery - 一款功能强大且方便的数据恢复程序,支持检测大量文件系统、操作系统和各种类型的驱动器:从简单的闪存驱动器到复杂的复合存储(各种级别的 RAID 阵列)。 该程序由执业专家开发,并…...
2023/10/23 mysql学习
数据库修改 show databases; 展示所有数据库 create database 数据库名; 创建数据库 create database if not exists 数据库名; 如果未创建过当前数据库名则创建 drop database 数据库名; drop database if exists 数据库名;用法和创建类似 删除数据库 use 数据库名; 跳…...
软考系统架构师知识点集锦六:项目管理
一、考情分析 二、考点精讲 2.1进度管理(时间管理) 进度管理:为了确保项目按期完成所需要的管理过程。 2.1.1过程 [WBS分解的基本要求] WBS的工作包是可控和可管理的,不能过于复杂。任务分解也不能过细,一般原则WBS的树形结构不超过6层。每个工作包要…...
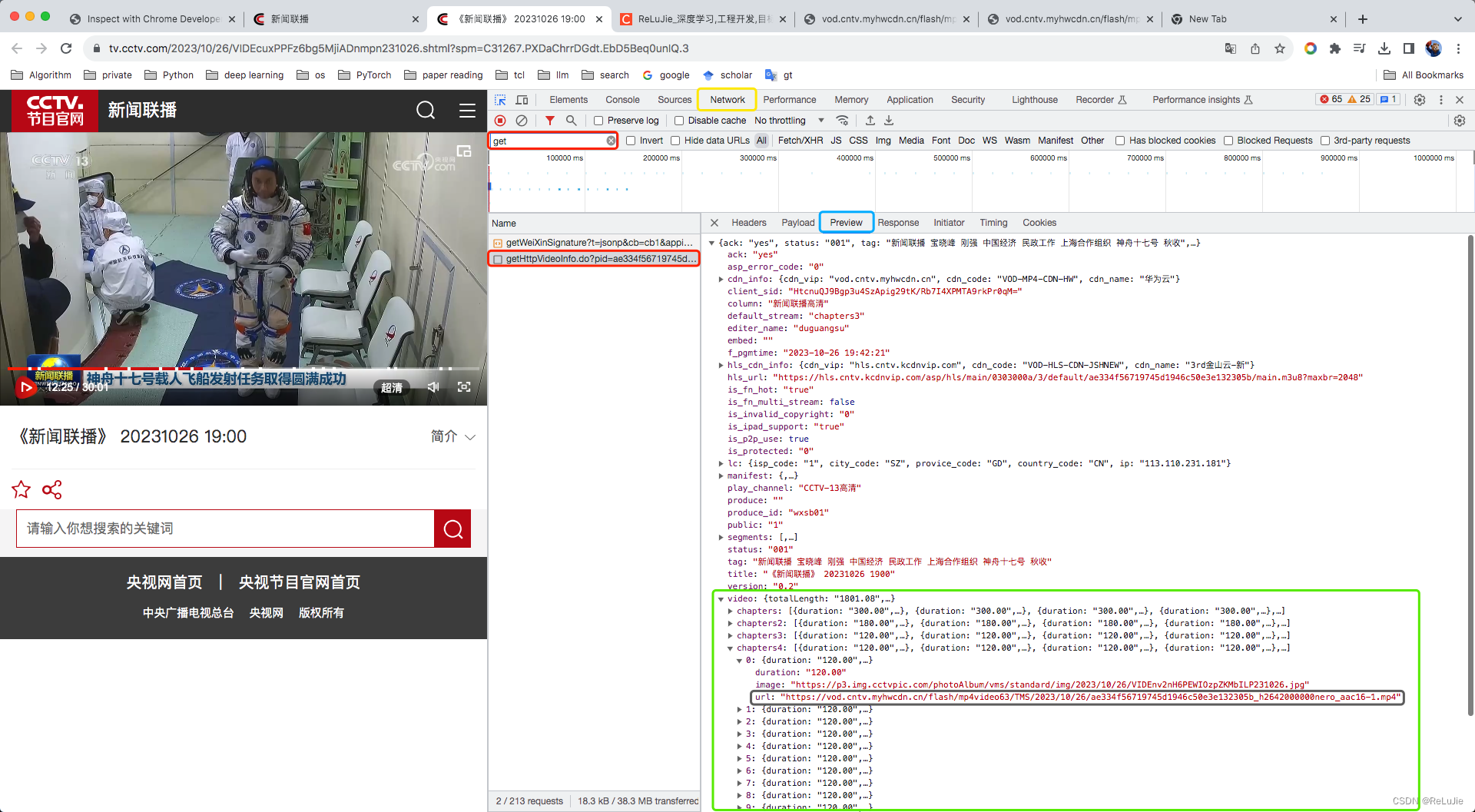
MacOS系统Chrome开发者模式下载在线视频
操作流程 # step1. 进入开发者模式 command option i # step2. 在搜索栏中搜索 getHttpVideoInfo.do?关键词 # step3. 在Preview的Json界面中找到video,然后选择不同resolution & duration的视频片段; # step4. 选择合适的video::chapters, 选择…...

uniapp v3+ts 使用 u-upload上传图片以及视频
上传图片方法 <u-upload :fileList"fileList1" afterRead"afterRead" delete"deletePic" name"file" multiple :maxCount"6"></u-upload> // maxCount 最大上传数const fileList1 ref([]);const file ref([…...

为什么虚拟dom会提高性能?
虚拟 DOM(Virtual DOM)是一种在前端开发中常用的技术,它可以提高性能并改善用户体验。虚拟 DOM 的原理和用处如下: 原理: 当页面状态发生变化时,虚拟 DOM 会以 JavaScript 对象的形式进行更新,而…...
2015年亚太杯APMCM数学建模大赛A题海上丝绸之路发展战略的影响求解全过程文档及程序
2015年亚太杯APMCM数学建模大赛 A题 海上丝绸之路发展战略的影响 原题再现 一带一路不是实体或机制,而是合作与发展的理念和主张。凭借现有有效的区域合作平台,依托中国与有关国家现有的双边和多边机制,利用古丝绸之路的历史象征࿰…...
js中HTMLCollection如何循环
//不带索引 let divCon document.getElementsByClassName("el-form-item__error"); if (divCon.length > 0) {for (var item of divCon) {console.log("打印:", item.innerText);} }//带有索引 let divCon document.getElementsByClassNam…...
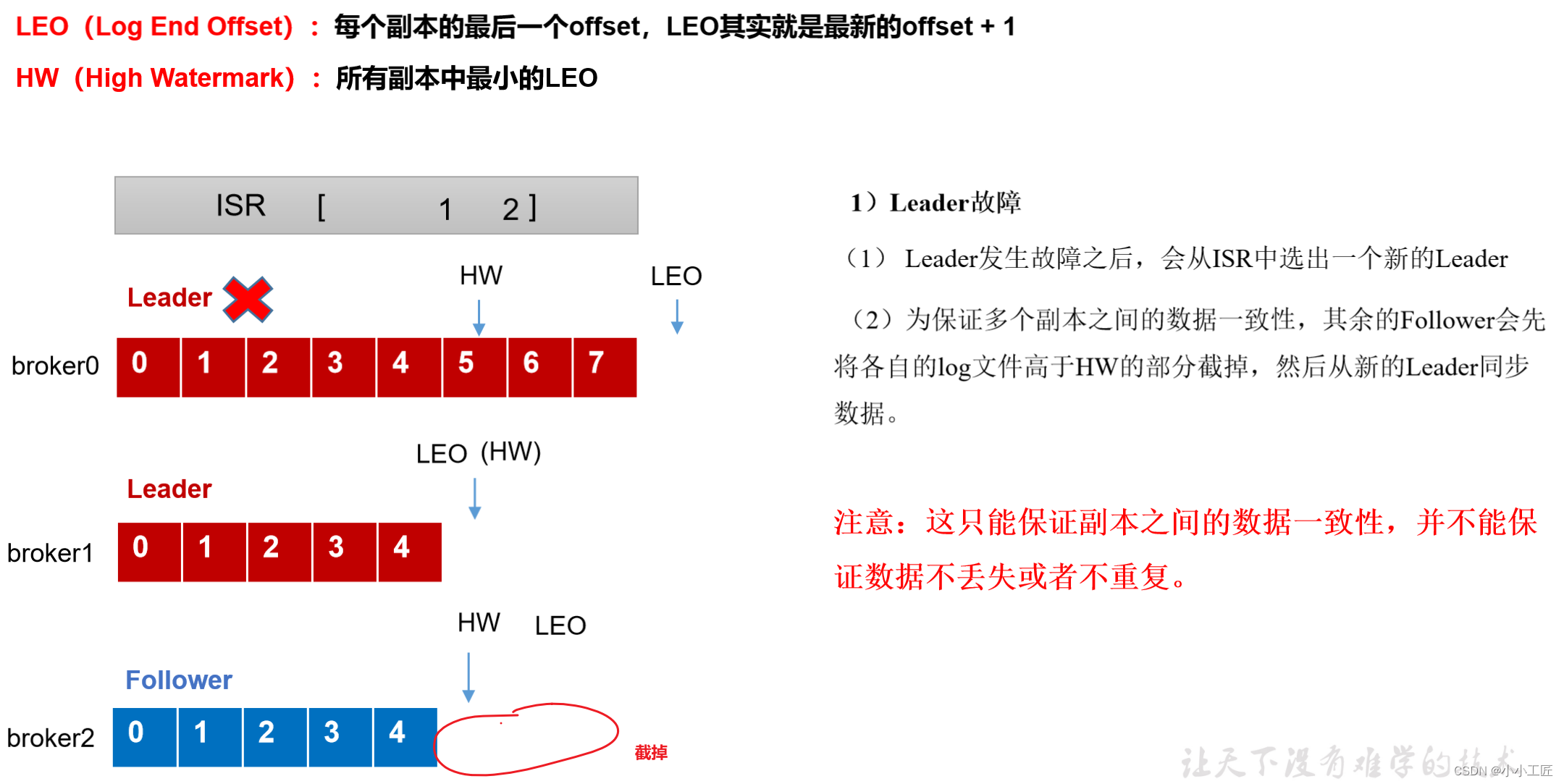
Kafka - 3.x 副本不完全指北
文章目录 kafka 副本的基本信息Leader选举过程Kafka Controllerkafka 分区副本Leader的选举流程实际演示① 查看first的详细信息,注意观察副本分布情况② 停掉hadoop103上的kafka进程③ 再次查看first的相信信息,观察副本分布④ 处理分区leader分布不均匀…...

二分归并法将两个数组合并
#define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> main() {int a[5] {1,3,4,5,6};int b[4] {2,7,8,9};int c[9];int m0, n0,k0;while (m < 5 && n < 4){if (a[m] < b[n]){c[k] a[m];//谁小谁先进数组m; k;}else{c[k] b[n];k; n;}}while (m <…...

ROS自学笔记十六:URDF优化_xacro文件
xacro 是一种 XML 扩展语言,用于创建和维护 URDF(Unified Robot Description Format)文件。它允许你使用参数化、宏和条件语句等功能来更灵活、更可维护地定义机器人模型。下面是关于 xacro 的详细解释: 1. 参数化(Par…...

XMLHttpRequest拦截请求和响应
环境: angular 实现: 拦截请求 向请求信息增加字段 拦截响应 过滤返回值 响应拦截: 根据angular使用的XMLHttpRequest 将对原本的请求转移到另一个将监听返回事件挂载到另一个世纪发送请求的xml上 使用get set 将客户端获取的res…...

前端 读取/导入 Excel文档
情况: 需要通过Excel表,将数据导入到数据库,但是后台人员出差了,我又只会PHP,没用过node,所以只能前端导入Excel文件,然后循环调用后台的单条添加接口了。 库: Excel.js(…...

聊聊springboot的TomcatMetricsBinder
序 本文主要研究一下springboot的TomcatMetricsBinder TomcatMetricsAutoConfiguration org/springframework/boot/actuate/autoconfigure/metrics/web/tomcat/TomcatMetricsAutoConfiguration.java Configuration(proxyBeanMethods false) ConditionalOnWebApplication C…...

《动手学深度学习 Pytorch版》 10.6 自注意力和位置编码
在注意力机制中,每个查询都会关注所有的键-值对并生成一个注意力输出。由于查询、键和值来自同一组输入,因此被称为 自注意力(self-attention),也被称为内部注意力(intra-attention)…...

2023年第四届MathorCup高校数学建模挑战赛——大数据竞赛B题 实现代码
根据之前发布的思路 第一步 进行数据合并 import pandas as pd# 读取所有附件的数据 data1 pd.read_excel(附件一.xlsx) data2 pd.read_excel(附件二.xlsx) data3 pd.read_excel(附件三.xlsx) data4 pd.read_excel(附件四.xlsx)# 根据商品编码将附件一和附件二连接 combi…...

larvel 中的api.php_Laravel 开发 API
Laravel10中提示了Target *classController does not exist,为什么呢? 原因是:laravel8开始写法变了。换成了新的写法了 解决方法一: 在路由数组加入App\Http\Controllers\即可。 <?phpuse Illuminate\Support\Facades\Route;…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
