旅游规划(树型dp)
W 市的交通规划出现了重大问题,市政府下定决心在全市各大交通路口安排疏导员来疏导密集的车流。
但由于人员不足,W 市市长决定只在最需要安排人员的路口安排人员。
具体来说,W 市的交通网络十分简单,由 n 个交叉路口和 n−1 条街道构成,交叉路口路口编号依次为 0,1,…,n−1 。
任意一条街道连接两个交叉路口,且任意两个交叉路口间都存在一条路径互相连接。
经过长期调查,结果显示,如果一个交叉路口位于 W 市交通网最长路径上,那么这个路口必定拥挤不堪。
所谓最长路径,定义为某条路径 p=(v1,v2,…,vk),路径经过的路口各不相同,且城市中不存在长度大于 k 的路径(因此最长路径可能不唯一)。
因此 W 市市长想知道哪些路口位于城市交通网的最长路径上。
输入格式
第一行包含一个整数 n
之后 n−1行每行两个整数 u,v,表示编号为 u和 v 的路口间存在着一条街道。
输出格式
输出包括若干行,每行包括一个整数——某个位于最长路径上的路口编号。
为了确保解唯一,请将所有最长路径上的路口编号按编号顺序由小到大依次输出。
数据范围
1≤n≤2×105
输入样例:
10 0 1 0 2 0 4 0 6 0 7 1 3 2 5 4 8 6 9输出样例:
0 1 2 3 4 5 6 8 9
两次dfs第一次求树的直径和当前点向下的最大值和次大值,第二次求当前点向上的最大值
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
constexpr int N=1e6+7;
int n,d1[N],d2[N],p[N],up[N];
int h[N],e[N],ne[N],idx;
int maxd;
void add(int a,int b){e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
void dfs_d(int u,int f){for(int i=h[u];i!=-1;i=ne[i]) {int j = e[i];if (j != f) {dfs_d(j, u);int dis = d1[j] + 1;if (dis > d1[u]) {d2[u] = d1[u], d1[u] = dis;p[u] = j;} else if (dis > d2[u]) {d2[u] = dis;}}}maxd= max(maxd,d1[u]+d2[u]);
}
void dfs_u(int u,int f){for(int i=h[u];i!=-1;i=ne[i]) {int j = e[i];if (j != f) {up[j]=up[u]+1;if(p[u]==j) up[j]= max(up[j],d2[u]+1);else up[j]= max(up[j],d1[u]+1);dfs_u(j,u);}}
}
int main(){memset(h,-1,sizeof h);scanf("%d",&n);for(int i=1;i<n;i++){int a,b;scanf("%d%d",&a,&b);add(a,b),add(b,a);}dfs_d(0,-1);dfs_u(0,-1);for (int i = 0; i < n; i++){int a[3] = {up[i], d1[i], d2[i]};sort(a, a + 3);if (a[1] + a[2] == maxd){printf("%d\n",i);}}return 0;
}
相关文章:
)
旅游规划(树型dp)
W 市的交通规划出现了重大问题,市政府下定决心在全市各大交通路口安排疏导员来疏导密集的车流。 但由于人员不足,W 市市长决定只在最需要安排人员的路口安排人员。 具体来说,W 市的交通网络十分简单,由 n 个交叉路口和 n−1 条街道…...

【C++】string类的模拟实现
当你将放弃作为一种习惯,你一辈子也不会有出息… 文章目录一、Default member functions1.Constructor2.Copy constructor(代码重构:传统写法和现代写法)3.operator(代码重构:传统写法和现代写法ÿ…...
——STL容器)
笔记(一)——STL容器
容器分类:序列式容器:每个元素都有固定位置,取决于插入的时机和地点,和元素无关,如vector、deque、list、stack、queue。关联式容器:元素位置取决于特定的排序准则,和插入顺序无关,如…...

红黑树
红黑树是一个相对的平衡,减少了旋转的消耗 一个节点不是红的就是黑的根节点是黑的一个节点是红的,孩子是黑的(没有连续的红色节点)对于每个节点,从该节点到后代节点的简单路径,都包含相同的黑色࿰…...
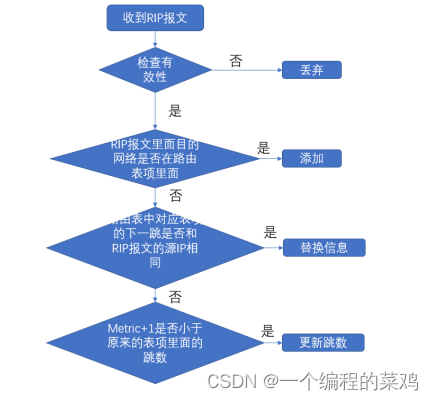
RIP路由协议的更新(电子科技大学TCP/IP第二次实验)
一.实验目的 1、掌握 RIP 协议在路由更新时的发送信息和发送方式 2、掌握 RIP 协议的路由更新算法 二.预备知识 1、静态路由选择和动态路由选择 2、内部网关协议和外部网关协议 3、距离向量路由选择 三.实验原理 RIP 协议(…...

基于JWT实现用户身份认证
常见场景 账号/密码登录、手机号验证码登录、微信扫码登录 解决方案 基于Session认证方案 什么是session认证方案 服务端生成httpsession认证(内存-sessionId)sessionId写到浏览器cookie浏览器请求的header中自动带sessionId到服务端服务端校验sessionId是否合法 优点 .…...
)
SaltStack 远程命令执行漏洞(CVE-2020-16846)
目录 (一)漏洞描述 (二)漏洞复现 1、在vulhub上启动docker 2、访问docker靶机 https /ip:8000...

SAP 详细解析成本收集器
成本收集器作为成本对象,主要应用于按期间进行成本核算的情况,在这种情况下会把产品创建为成本收集器,实际成本的收集和差异的结算全部按照成本收集器进行处理,财务的成本分析也针对成本收集器进行。 成本收集器是按期间核算&am…...

Vision Transformer学习了什么-WHAT DO VISION TRANSFORMERS LEARN? A VISUAL EXPLORATION
WHAT DO VISION TRANSFORMERS LEARN? A VISUAL EXPLORATION 文章地址 代码地址 摘要 视觉转换器( Vision Transformers,ViTs )正在迅速成为计算机视觉的事实上的架构,但我们对它们为什么工作和学习什么知之甚少。虽然现有研究对卷积神经网络的机制进…...

一种全新的图像滤波理论的实验(三)
一、前言 2023年02月22日,我发布了滤波后,为针对异常的白色和黑色像素进行处理的实验,本次发布基于上下文处理的方案的实验,目的是通过基于加权概率模型滤波后,在逆滤波时直接修复大量的白色和黑色的异常像素…...
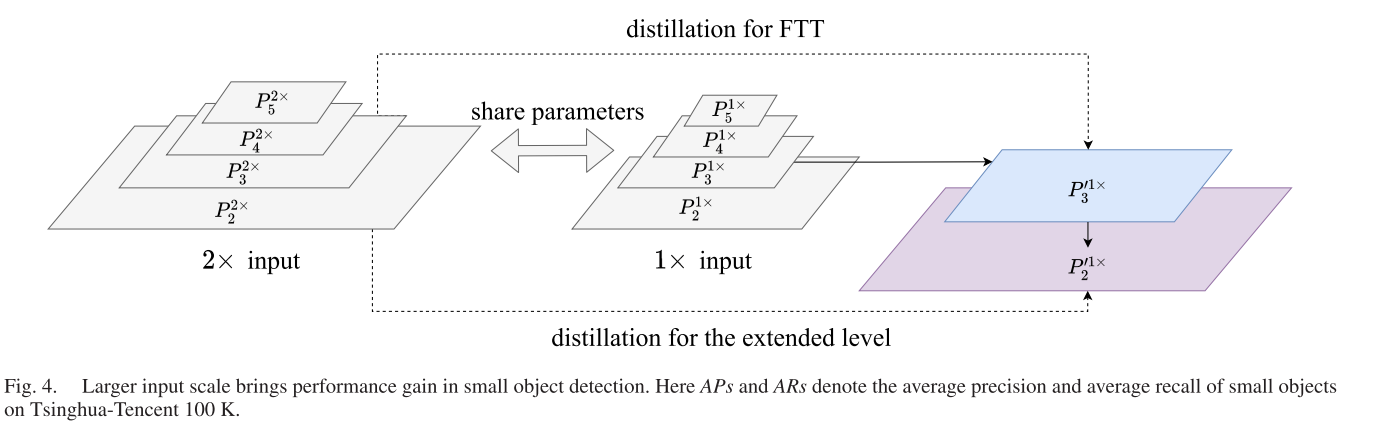
CV——day79 读论文:基于小目标检测的扩展特征金字塔网络
Extended Feature Pyramid Network for Small Object DetectionI. INTRODUCTIONII. RELATED WORKA. 深层物体探测器B. 跨尺度特征C. 目标检测中的超分辨率III. OUR APPROACHA. 扩展特征金字塔网络B. 特征纹理传输C. 交叉分辨蒸馏IV. EXPERIMENTSA. Experimental Settings1&…...
智能家居项目(五)测试串口功能
目录 一、写一个单独测试串口的demo 二、直接运行上一篇智能家居的代码 一、写一个单独测试串口的demo 1、TTL串口与树莓派的连接方式 (1)TTL的RXD和TXD针脚连接到树莓的TXD和RXD上(T–>R R–>T),交叉连&…...

2023年全国最新道路运输从业人员精选真题及答案7
百分百题库提供道路运输安全员考试试题、道路运输从业人员考试预测题、道路安全员考试真题、道路运输从业人员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 71.根据《中华人民共和国安全生产法》,生产经营单位…...

python的所有知识点(含讲解),不看就亏死了
目录 简介 特点 搭建开发环境 版本 hello world 注释 文件类型 变量 常量 数据类型 运算符和表达式 控制语句 数组相关 函数相关 字符串相关 文件处理 对象和类,注:不是那个对象!!!!&…...

【Servlet篇】Response对象详细解读
文章目录Response 继承体系Response 设置响应数据设置响应行数据设置响应头数据设置响应体数据Response 重定向Response 响应字符数据Response 响应字节数据Response 继承体系 前面说到,我们使用 Request 对象来获取请求数据,使用 Response 对象来设置响…...

SAP FICO期初开账存货导入尾差
一、问题 1.AFS物料网格级别库存导入先除再乘有尾差: 旧系统数据迁移自两个系统:一个管理数量账(网格级别),一个管理金额账(物料级别) 2.MB52分工厂与MB5L分工厂统计差异: M…...
微信商城小程序怎么做_分享实体店做微信商城小程序制作步骤
各行各业都在用微商城小程序开店,不管是餐饮店还是便利店,还是五金店。都是可以利用微信小程序开一个线上店铺。实现线上跟线下店铺更加全面的结合。维护好自己的老客户。让您的客户给您拉新,带来新客户。小程序经过这几年的快速发展和不断升…...

【moment.js】时间格式化插件
Moment.js 用于在JavaScript中解析,验证,操作和显示日期和时间。是一款在项目中使用频率极高的时间格式化工具,Ant Design Vue 组件中就是使用它来处理时间的。 安装 npm install moment --save # npm yarn add moment # Ya…...

微信小程序开发【壹】
随手拍拍💁♂️📷 日期: 2023.02.24 地点: 杭州 介绍: 2023.02.24上午十点,路过学院的教学楼时🏢,突然看见了一团粉红色。走进一看是一排梅花🌸,赶在它们凋零前,将它们定格在我的相…...

2 k-近邻算法
0 问题引入 想一想:下面图片中有三种豆,其中三颗豆品种未知,如何判断他们类型? 1 KNN概述 1.1 KNN场景 电影可以按照题材分类,那么如何区分 动作片 和 爱情片 呢? 动作片:打斗次数更多爱情…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
