15、条件概率、全概率公式、贝叶斯公式、马尔科夫链
条件概率
定义:设A、B是两个事件,且,P(A) > 0 则称  为事件A发生的条件下事件B的条件概率
为事件A发生的条件下事件B的条件概率
对这个式子进行变形,即可得到概率的乘法公式:
P(A) > 0 时,则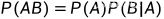
P(B) > 0 时,则
乍一看,这个式子不就是把除法形式写成了乘法形式嘛,不然不然,这个区别是本质的,分母不为0很关键,而且看法也不同:前面的是条件概率,后面的是概率的乘法公式。
概率的乘法公式,起源于概率的乘法原理,一件事情发生的概率等于造成这件事发生的接连发生的事件概率的乘积,如果要让A,B同时发生,那么就让其中一个先发生,不妨设为A吧,A发生以后B再发生,这样子的话,A,B就会同时发生了,根据概率的乘法原理如下

概率的乘法公式的n个事件的形式:
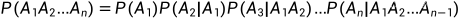
如果要使n件事件同时发生,不妨先发生 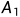 ,接着再发生
,接着再发生  ,
,
全概率公式
若事件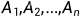 满足下列两条
满足下列两条
则称 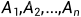 为完备事件组
为完备事件组
全概率公式如:

以n=3为例:
比如一件事情的结果就只有三种 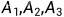 ,也知道它们发生的概率,但是呢,这时候偏偏有一个事件B也发生了,我们的目的是找出B发生的概率,于是呢,我们让B与
,也知道它们发生的概率,但是呢,这时候偏偏有一个事件B也发生了,我们的目的是找出B发生的概率,于是呢,我们让B与 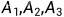 发生联系,从而进行试验,可以得到各自的条件概率
发生联系,从而进行试验,可以得到各自的条件概率 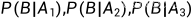 ,那么这就足够了,我们就可以得到事件B发生的概率
,那么这就足够了,我们就可以得到事件B发生的概率
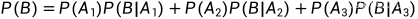
贝叶斯公式
贝叶斯定理的发明者 托马斯·贝叶斯 提出了一个很有意思的假设:“如果一个袋子中共有 10 个球,分别是黑球和白球,但是我们不知道它们之间的比例是怎么样的,现在,仅通过摸出的球的颜色,是否能判断出袋子里面黑白球的比例?”
简单而言就是已知结果找原因
设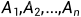 是完备事件组,且
是完备事件组,且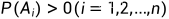
B 为任意事件,P(B) > 0,则
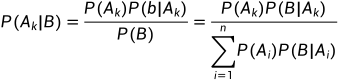
对于这个公式的理解主要靠上面那句话。什么是结果?什么又是原因?对于全概率公式,我们说是为了求事件B发生的概率所做的试验,这些就是结果了,那么反过来,我们找原因,这些完备事件在B发生时的条件概率就是我们所要查照的原因了。
通常把 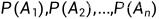 叫做先验概率,就是做试验前的概率,就是经验了;而把
叫做先验概率,就是做试验前的概率,就是经验了;而把  叫做后验概率,在统计决策中十分重要,由此得到的决策叫做贝叶斯决策。也就是说我们在对经验不断地更新和修正,当然是利用生活实践,即所谓试验。(又是一个人生哲理,对于很多事情,就是要不断地利用当前的经验来进行试错,不断地修正,从而达到自我的一个最佳状态
叫做后验概率,在统计决策中十分重要,由此得到的决策叫做贝叶斯决策。也就是说我们在对经验不断地更新和修正,当然是利用生活实践,即所谓试验。(又是一个人生哲理,对于很多事情,就是要不断地利用当前的经验来进行试错,不断地修正,从而达到自我的一个最佳状态
马尔科夫链
定义一种表述方法,考虑只取有限个或可数个值的随机过程  若
若  ,则称过程在 n 时刻处于状态 i。
,则称过程在 n 时刻处于状态 i。
马尔可夫性:给定过去的状态  和现在的状态
和现在的状态  ,将来的状态
,将来的状态  的条件分布与过去的状态独立,只依赖于现在的状态,这样的性质称为马尔可夫性。
的条件分布与过去的状态独立,只依赖于现在的状态,这样的性质称为马尔可夫性。
如果我们用 A表示过去的状态,用 B 表示现在的状态,而用 C 表示将来的状态,即

则马尔科夫性可以用条件概率直观表示为

等价推出

因此马尔可夫性也可以理解为在已知现在状态的条件下,过去与将来相互独立
马尔科夫链:设随机过程  的状态空间 I 有限或可列,如果它具有马尔科夫性,即对任意的状态
的状态空间 I 有限或可列,如果它具有马尔科夫性,即对任意的状态 和任意的
和任意的  有
有

则称随机过程  是马尔科夫链,简称马氏链
是马尔科夫链,简称马氏链
把具有马尔可夫性的随机过程称为马尔可夫过程。
马尔可夫链是离散时间离散状态的马尔可夫过程。
泊松过程是连续时间离散状态的马尔可夫过程。
布朗运动是连续时间连续状态的马尔科夫过程。
转移概率和转移矩阵
考虑马尔科夫链  及其状态空间
及其状态空间  ,将条件概率定义为
,将条件概率定义为

用来表示过程在 m 时刻处于状态 i 的条件下,经过 n 步后转移到状态 j 的转移概率。 由于概率是非负的,且过程在 m 时刻从任何一个状态 i 出发,到 m + n 时刻必须转移到 I 中的某个状态,所以有

时齐的马尔可夫链:如果 不依赖于 n,则过程
不依赖于 n,则过程  是时齐的马尔可夫链。定义马尔可夫链的一步转移概率为
是时齐的马尔可夫链。定义马尔可夫链的一步转移概率为
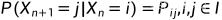
一步转移概率  的含义是处在状态 i 的过程下一次转移到状态 j的概率,显然一步转移概率也具有如下性质:
的含义是处在状态 i 的过程下一次转移到状态 j的概率,显然一步转移概率也具有如下性质:

不妨设状态空间为自然数集  ,定义一步转移概率矩阵为
,定义一步转移概率矩阵为

显然一步转移概率矩阵 P 的所有元素都是非负的,且每一行的元素之和为 1 。
在马尔可夫链是时齐的情形下,条件概率  只与 i , j 以及时间间隔 n 有关,定义马尔可夫链的 n 步转移概率为
只与 i , j 以及时间间隔 n 有关,定义马尔可夫链的 n 步转移概率为

其含义是处在状态 i 过程将在 n 次转移之后处于状态 j 的概率。类似的可以定义 n 步转移概率矩阵为
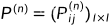
如果想判断一个马尔可夫链是时齐的,只需要证明它的一步转移概率与时间 n 无关即可
相关文章:
15、条件概率、全概率公式、贝叶斯公式、马尔科夫链
条件概率定义:设A、B是两个事件,且,P(A) > 0 则称 为事件A发生的条件下事件B的条件概率对这个式子进行变形,即可得到概率的乘法公式:P(A) > 0 时,则P(B) > 0 时,则乍一看,…...
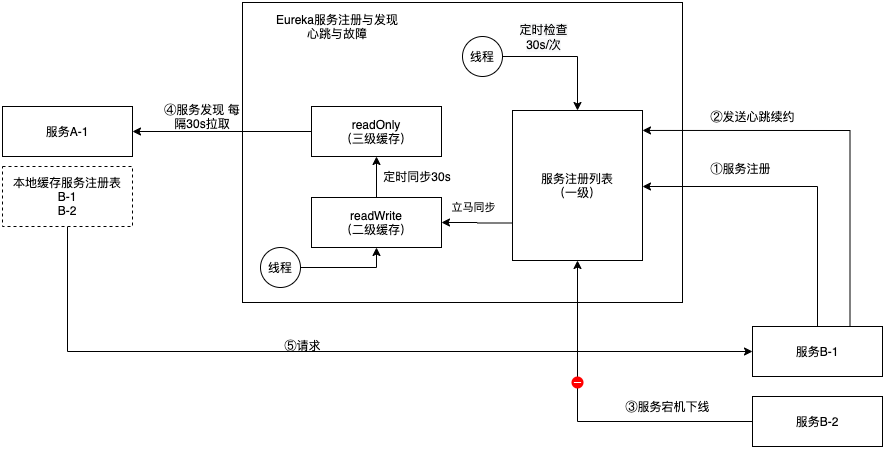
Eureka服务注册与发现
注册中心是分布式开发的核心组件之一,而Eureka是spring cloud推荐的注册中心实现。简单分析一下Eureka的原理。Eureka基础概念与流程1、服务注册在微服务架构中,一个服务提供者本质上也是一个Eureka客户端。启动时,会调用Eureka所提供的服务注…...

20230226 引用类型和指针类型的区别 - chatGPT
绝了,把chatGPT当百度之后真爽! 引用类型和指针类型都是C语言中的重要概念,它们都提供了访问和操作内存的方法,但它们之间有几个关键的区别。 1. 定义和初始化方式不同 指针类型的变量定义和初始化的方式是通过使用*符号来声明…...
《操作系统》——第二章 进程与线程
目录 2.1.1进程的概念、组成、特征 2.1.2进程的状态与转换、进程的组织 2.1.3进程控制 2.1.4进程通信 2.1.5线程的概念 2.1.6线程的实现方式和多线程模型 2.2.1调度的概念、层次 2.2.2进程调度的时机、切换与过程、方式 2.2.4调度算法的评价指标 2.2.5调度算法(1) 2…...

网络原理之初识
目录 一. 网络互连 1. 局域网 2. 广域网 二. 网络通信基础 1. IP 地址 2. 端口号 3. 网络协议 4. 协议分层 5. TCP/IP 五层网络模型 (简述) 6. 网络数据传输的基本流程 一. 网络互连 随着时代的发展,越来越需要计算机之间互相通信&am…...
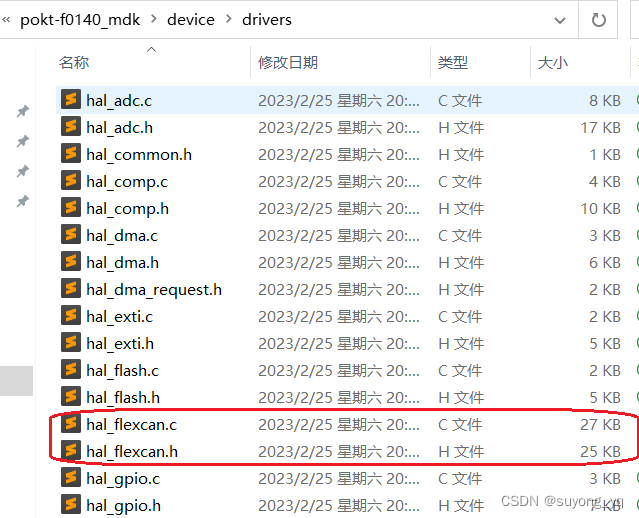
CAN总线开发一本全(4) - FlexCAN的驱动程序
CAN总线开发一本全(4) - FlexCAN的驱动程序 苏勇,2023年2月 文章目录CAN总线开发一本全(4) - FlexCAN的驱动程序引言从MindSDK获取FlexCAN驱动程序数据结构配置通信引擎的结构体类型访问MB的结构体类型配置ID过滤器的…...

如何分析linux tcp/ip 丢包问题
引用手把手教你用Dropwatch诊断问题通过dropwatch定位系统内核丢包Finding out if/why a server is dropping packetsgithub source coed: pavel-odintsov/drop_watchHow to drop a packet in Linux in more ways than one试试Linux下的ip命令,ifconfig已经过时了Ho…...
)
旅游规划(树型dp)
W 市的交通规划出现了重大问题,市政府下定决心在全市各大交通路口安排疏导员来疏导密集的车流。 但由于人员不足,W 市市长决定只在最需要安排人员的路口安排人员。 具体来说,W 市的交通网络十分简单,由 n 个交叉路口和 n−1 条街道…...

【C++】string类的模拟实现
当你将放弃作为一种习惯,你一辈子也不会有出息… 文章目录一、Default member functions1.Constructor2.Copy constructor(代码重构:传统写法和现代写法)3.operator(代码重构:传统写法和现代写法ÿ…...
——STL容器)
笔记(一)——STL容器
容器分类:序列式容器:每个元素都有固定位置,取决于插入的时机和地点,和元素无关,如vector、deque、list、stack、queue。关联式容器:元素位置取决于特定的排序准则,和插入顺序无关,如…...

红黑树
红黑树是一个相对的平衡,减少了旋转的消耗 一个节点不是红的就是黑的根节点是黑的一个节点是红的,孩子是黑的(没有连续的红色节点)对于每个节点,从该节点到后代节点的简单路径,都包含相同的黑色࿰…...
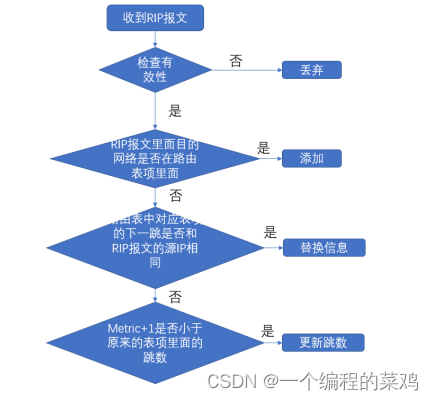
RIP路由协议的更新(电子科技大学TCP/IP第二次实验)
一.实验目的 1、掌握 RIP 协议在路由更新时的发送信息和发送方式 2、掌握 RIP 协议的路由更新算法 二.预备知识 1、静态路由选择和动态路由选择 2、内部网关协议和外部网关协议 3、距离向量路由选择 三.实验原理 RIP 协议(…...

基于JWT实现用户身份认证
常见场景 账号/密码登录、手机号验证码登录、微信扫码登录 解决方案 基于Session认证方案 什么是session认证方案 服务端生成httpsession认证(内存-sessionId)sessionId写到浏览器cookie浏览器请求的header中自动带sessionId到服务端服务端校验sessionId是否合法 优点 .…...
)
SaltStack 远程命令执行漏洞(CVE-2020-16846)
目录 (一)漏洞描述 (二)漏洞复现 1、在vulhub上启动docker 2、访问docker靶机 https /ip:8000...

SAP 详细解析成本收集器
成本收集器作为成本对象,主要应用于按期间进行成本核算的情况,在这种情况下会把产品创建为成本收集器,实际成本的收集和差异的结算全部按照成本收集器进行处理,财务的成本分析也针对成本收集器进行。 成本收集器是按期间核算&am…...

Vision Transformer学习了什么-WHAT DO VISION TRANSFORMERS LEARN? A VISUAL EXPLORATION
WHAT DO VISION TRANSFORMERS LEARN? A VISUAL EXPLORATION 文章地址 代码地址 摘要 视觉转换器( Vision Transformers,ViTs )正在迅速成为计算机视觉的事实上的架构,但我们对它们为什么工作和学习什么知之甚少。虽然现有研究对卷积神经网络的机制进…...

一种全新的图像滤波理论的实验(三)
一、前言 2023年02月22日,我发布了滤波后,为针对异常的白色和黑色像素进行处理的实验,本次发布基于上下文处理的方案的实验,目的是通过基于加权概率模型滤波后,在逆滤波时直接修复大量的白色和黑色的异常像素…...
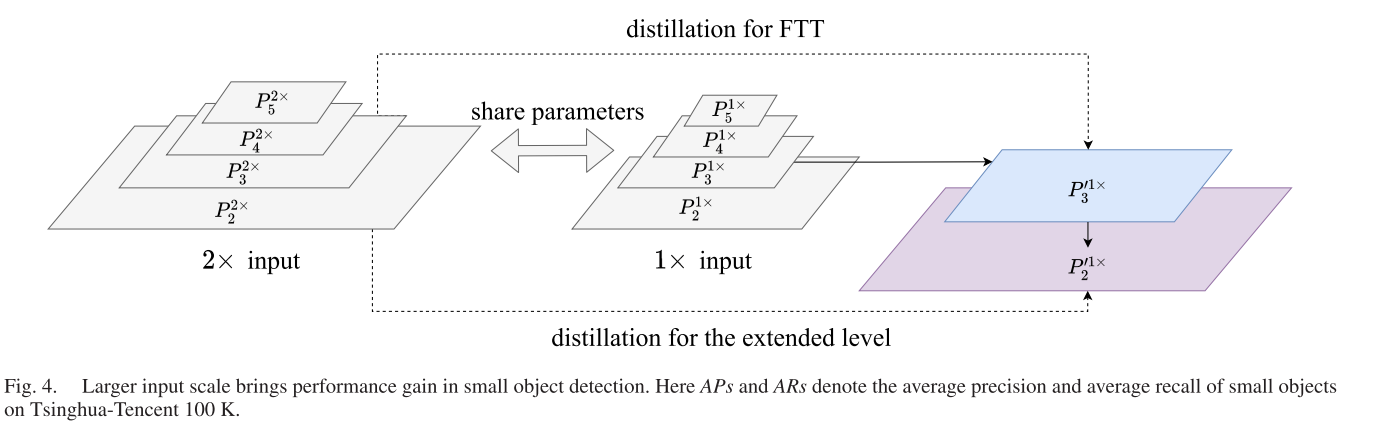
CV——day79 读论文:基于小目标检测的扩展特征金字塔网络
Extended Feature Pyramid Network for Small Object DetectionI. INTRODUCTIONII. RELATED WORKA. 深层物体探测器B. 跨尺度特征C. 目标检测中的超分辨率III. OUR APPROACHA. 扩展特征金字塔网络B. 特征纹理传输C. 交叉分辨蒸馏IV. EXPERIMENTSA. Experimental Settings1&…...
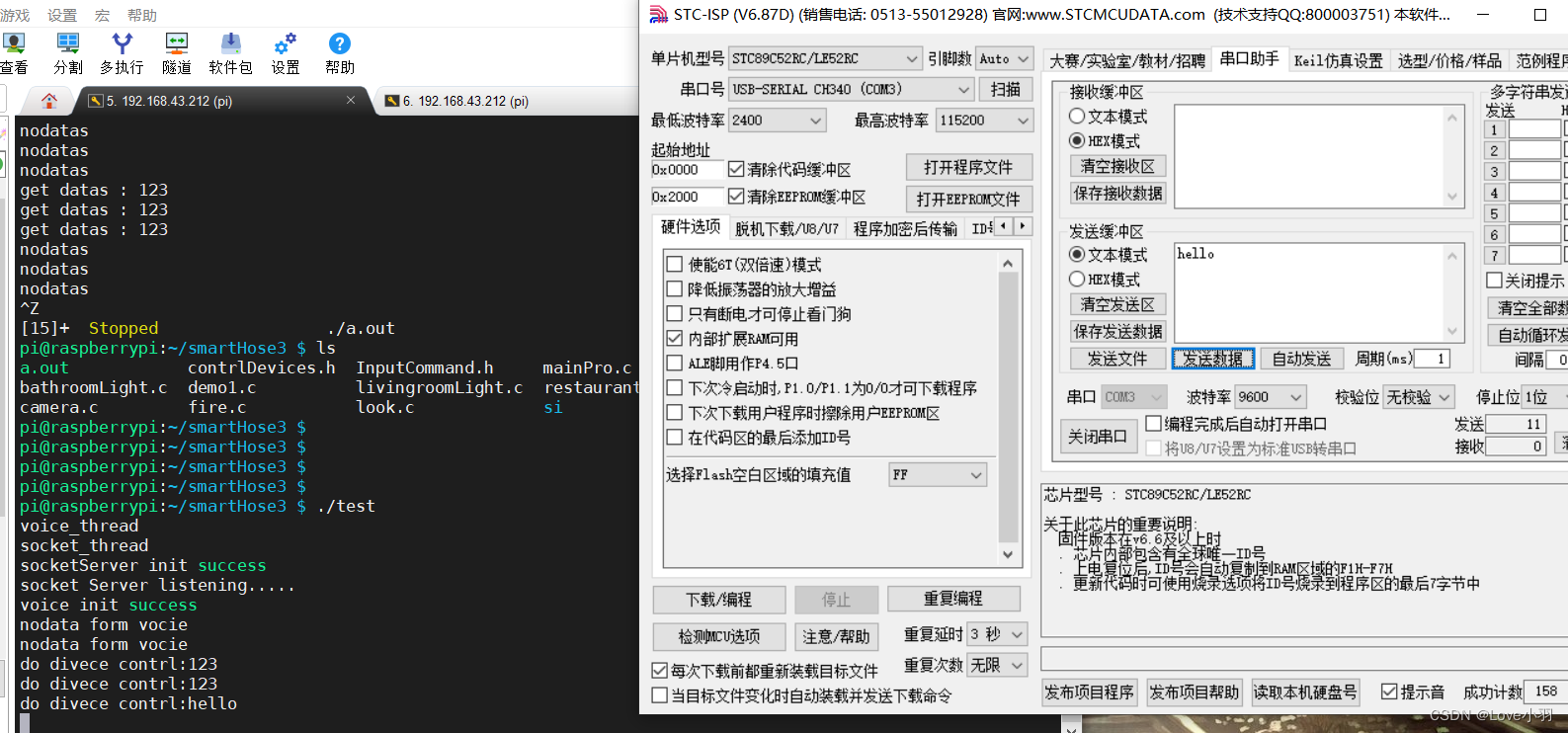
智能家居项目(五)测试串口功能
目录 一、写一个单独测试串口的demo 二、直接运行上一篇智能家居的代码 一、写一个单独测试串口的demo 1、TTL串口与树莓派的连接方式 (1)TTL的RXD和TXD针脚连接到树莓的TXD和RXD上(T–>R R–>T),交叉连&…...

2023年全国最新道路运输从业人员精选真题及答案7
百分百题库提供道路运输安全员考试试题、道路运输从业人员考试预测题、道路安全员考试真题、道路运输从业人员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 71.根据《中华人民共和国安全生产法》,生产经营单位…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...


