【Codeforces】 CF79D Password
题目链接
CF方向
Luogu方向
题目解法
看到区间异或,一个经典的套路是做差分,我们即在 l l l 处异或一次,在 r + 1 r+1 r+1 处异或一次,然后前缀和起来
于是我们可以将问题转化成:有一个序列初始全 0 0 0,每次可以把相隔 a i a_i ai 的数都 ⊕ 1 \oplus 1 ⊕1,求最少将其变成一个状态的步数
考虑 k k k 的范围很小,所以为 1 1 1 的地方一共只有 2 k 2k 2k 个
这里有一个非常重要的 t r i c k trick trick:在异或操作中,如果需要把 x , y x,y x,y 同时异或 1 1 1,其他不变,每次可以同时修改相隔 a i a_i ai 的位置的异或值,那么这个问题等价于建出图来从 x x x 到 y y y 的最短路
然后发现直接状压跑最短路即可,时间复杂度 O ( 2 k k 2 ) O(2^kk^2) O(2kk2)
不难优化成 O ( 2 k k ) O(2^kk) O(2kk),但我直接 998 m s 998ms 998ms 用 O ( 2 k k 2 ) O(2^kk^2) O(2kk2) 的做法艹过去了,就懒得改了
O ( 2 k k 2 ) O(2^kk^2) O(2kk2) 的代码:
#include <bits/stdc++.h>
using namespace std;
const int N=10100,M=2000100;
int n,m,k,a[110],x[30],dis[N];
int f[(1<<20)+100],D[30][30];
int e[M],ne[M],h[N],idx;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
queue<int> que;
void bfs(int S){memset(dis,0x3f,sizeof(dis));que.push(S),dis[S]=0;while(!que.empty()){int u=que.front();que.pop();for(int i=h[u];~i;i=ne[i]) if(dis[u]+1<dis[e[i]])dis[e[i]]=dis[u]+1,que.push(e[i]);}
}
void add(int x,int y){ e[idx]=y,ne[idx]=h[x],h[x]=idx++;}
int main(){n=read(),k=read(),m=read();for(int i=0;i<k;i++) x[i]=read();for(int i=1;i<=m;i++) a[i]=read();for(int i=0;i<k;i++) x[i+k]=x[i]+1;memset(h,-1,sizeof(h));for(int i=1;i<=m;i++)for(int j=1;j<=n-a[i]+1;j++)add(j,j+a[i]),add(j+a[i],j);for(int i=0;i<k<<1;i++){bfs(x[i]);for(int j=0;j<k<<1;j++) D[i][j]=dis[x[j]];}memset(f,0x3f,sizeof(f));f[0]=0;for(int S=0;S<1<<(k<<1);S++)for(int i=0;i<k<<1;i++) if(S>>i&1)for(int j=0;j<k<<1;j++) if(S>>j&1) if(i!=j)f[S]=min(f[S],f[S^(1<<i)^(1<<j)]+D[i][j]);printf("%d\n",f[(1<<(k<<1))-1]>1e9?-1:f[(1<<(k<<1))-1]);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}相关文章:

【Codeforces】 CF79D Password
题目链接 CF方向 Luogu方向 题目解法 看到区间异或,一个经典的套路是做差分,我们即在 l l l 处异或一次,在 r 1 r1 r1 处异或一次,然后前缀和起来 于是我们可以将问题转化成:有一个序列初始全 0 0 0,…...

叛乱沙漠风暴server安装 ubuntu 22.04
最新版沙暴已经不支持centos了,还是使用ubuntu比较顺利 官方文档: https://sandstorm-support.newworldinteractive.com/hc/en-us/articles/360049211072-Server-Admin-Guide // 安装steamcmd依赖 sudo add-apt-repository multiverse sudo apt inst…...

ES6中的新增属性——解构赋值
首先我们要创建一个假数据,我们现在要取出user中的id和名称,如下: let user JSON.parse(sessionStorage.getItem(userInfo)) let id user.id; let name user.name; 非常的麻烦,我们需要一项一项的获取,这个时候可…...
行业追踪,2023-10-27
自动复盘 2023-10-27 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
Qt QWebEngine 更换语言
背景 使用Qt QWebEngine开发的应用,在一些场景下,会显示英文文本,比如右键、JS弹出的对话框,所以需要进行汉化,更改语言。 准备翻译文件 Qt有提供翻译好的ts文件,我们可以直接下载ts文件qtwebengine_zh_…...

Docker一键开启、停止和删除所有容器
开启所有运行的容器: docker start $(docker ps -aq) 这里,docker ps -aq 列出了所有容器的ID,然后 docker start 命令用于开启这些容器。 停止所有运行的容器: docker stop $(docker ps -aq) 同理,docker ps -aq…...

2016年亚太杯APMCM数学建模大赛B题化学元素对变形钢筋性能的影响求解全过程文档及程序
2016年亚太杯APMCM数学建模大赛 B题 化学元素对变形钢筋性能的影响 原题再现 热轧带肋钢筋通常被称为变形钢筋,它主要用于钢筋混凝土构件的骨架,在使用中需要一定的机械强度、弯曲和变形性能、制造焊接性。钢中的化学成分是影响热轧钢最终组织性能的基…...

美颜SDK集成指南:为应用添加视频美颜功能
随着社交媒体和直播应用的兴起,视频美颜功能已成为用户追求的一项热门特性。用户希望能够在拍摄照片或进行实时视频直播时,使用美颜功能来增强其外观。为了满足这一需求,开发者可以考虑集成美颜SDK,为其应用增加这一吸引人的功能。…...

AquilaChat2-34B 主观评测接近GPT3.5水平,最新版本Base和Chat权重已开源!
两周前,智源研究院发布了最强开源中英双语大模型AquilaChat2-34B 并在 22项评测基准中综合能力领先,广受好评。为了方便开发者在低资源上运行 34B 模型,智源团队发布了 Int4量化版本,AquilaChat2-34B 模型用7B量级模型相近的GPU资…...

useGeneratedKeys=“true“ keyProperty=“id“
1、xml中 useGeneratedKeys"true" keyProperty"id"2、db id bigint(20) AUTO_INCREMENT 3、场景 一般用于 先将DO写入dbinsert成功后,再将JDBC自增主键值AUTO_INCREMENT,回写到DO的id属性字段后续可能会从DO中获取此id值进行查询…...
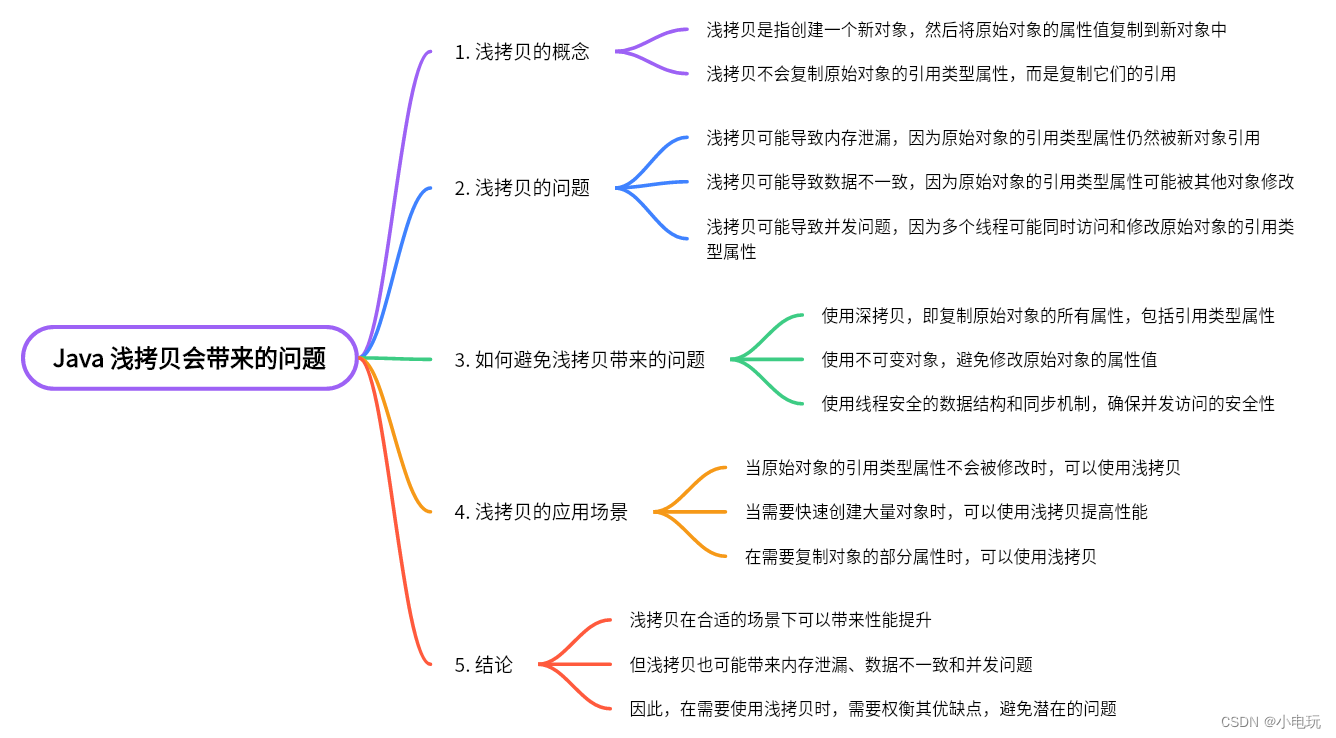
Java 浅拷贝会带来的问题
Java 浅拷贝会带来的问题 一,常见问题 Java 中的浅拷贝是指在对象拷贝时,只复制对象的引用,而不是对象本身。这意味着浅拷贝会导致多个对象共享同一块内存空间,当一个对象修改共享内存时,其他对象也会受到影响。 下…...

Monocle 3 | 太牛了!单细胞必学R包!~(二)(寻找marker及注释细胞)
1写在前面 昨天又是不睡觉的一天,晚上还被家属讲了一通,理由是我去急诊了,没有在办公室待着,他老公疼没人去看。🫠 我的解释是只有我一个值班医生,不可能那么及时,而且也不是什么急症啊。&#…...
简述JVM
文章目录 JVM简介JVM运行时数据区堆(线程共享)方法区/元空间/元数据区(线程共享)栈程序计数器 JVM类加载类加载过程双亲委派模型 垃圾回收机制(GC)判断对象是否为垃圾判断是否被引用指向 如何清理垃圾, 释放对象? JVM简介 JVM 是 Java Virtual Machine 的简称, 意为Java虚拟机…...

【多线程面试题 六】、 如何实现线程同步?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官: 如何实现线程同步&…...
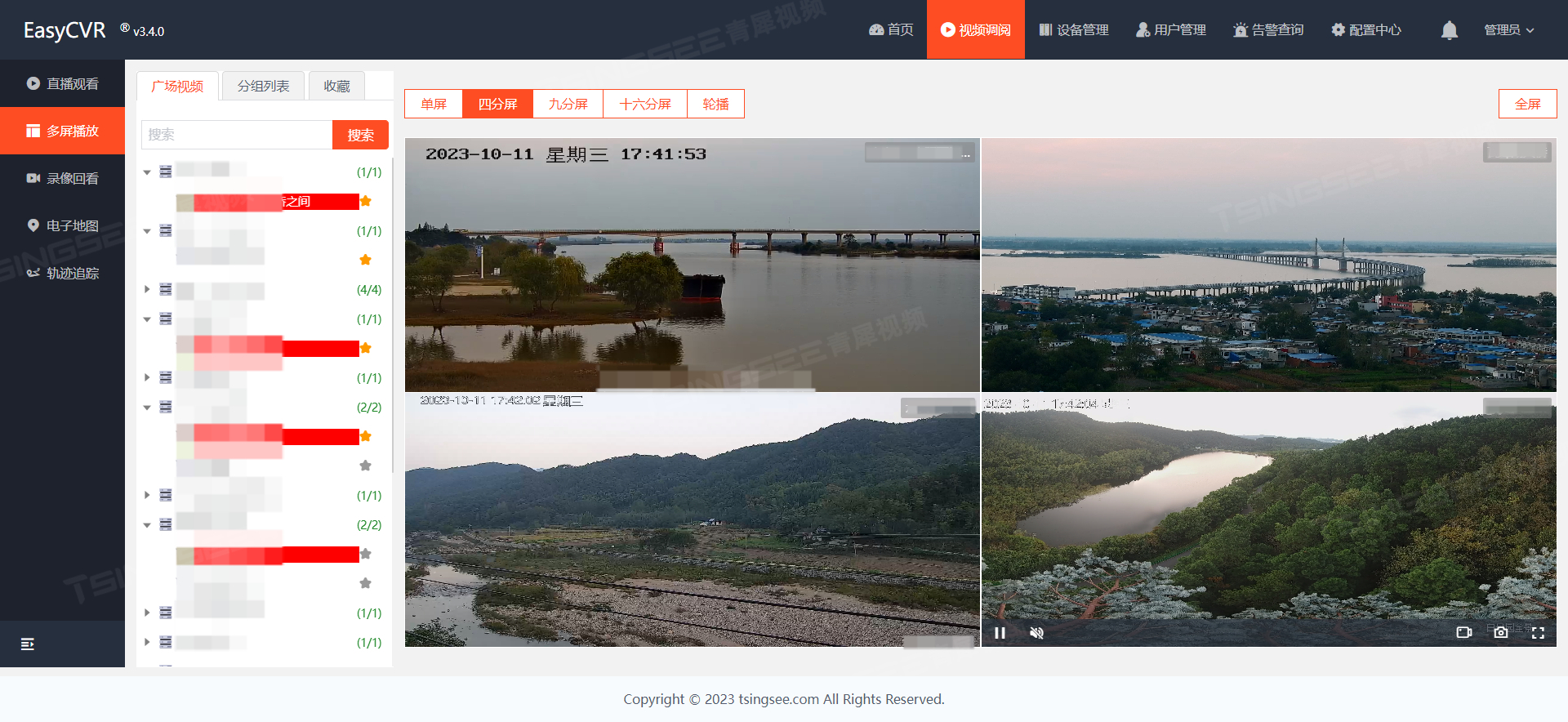
地面文物古迹保护方案,用科技为文物古迹撑起“智慧伞”
一、行业背景 当前,文物保护单位的安防系统现状存在各种管理弊端,安防系统没有统一的平台,系统功能不足、建设标准不同,产品和技术多样,导致各系统独立,无法联动,形成了“信息孤岛”。地面文物…...
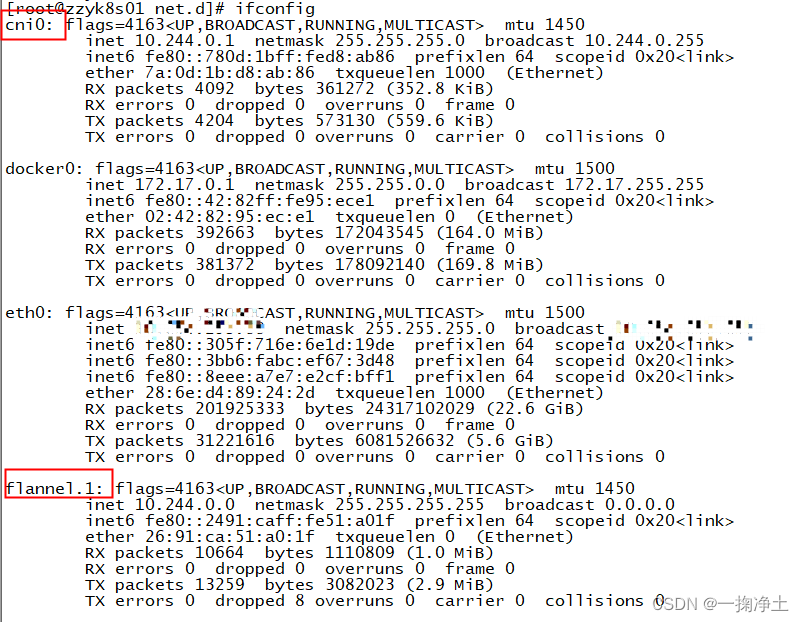
k8s之Flannel网络插件安装提示forbidden无权限
一、问题描述 在安装k8s的网络插件时,提示如下信息,各种forbidden无权限 [rootzzyk8s01 scripts]# kubectl apply -f kube-flannel.yml Error from server (Forbidden): error when retrieving current configuration of: Resource: "policy/v1b…...
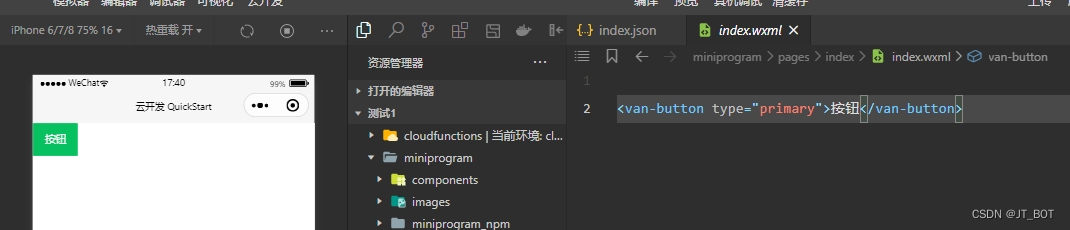
在微信小程序云开发中引入Vant Weapp组件库
介绍 Vant 是一个轻量、可靠的移动端组件库,于 2017 年开源。 目前 Vant 官方提供了 Vue 2 版本、Vue 3 版本和微信小程序版本,并由社区团队维护 React 版本和支付宝小程序版本。 介绍 - Vant Weapp (youzan.github.io) Vant Weapp需要安装 node.js&…...
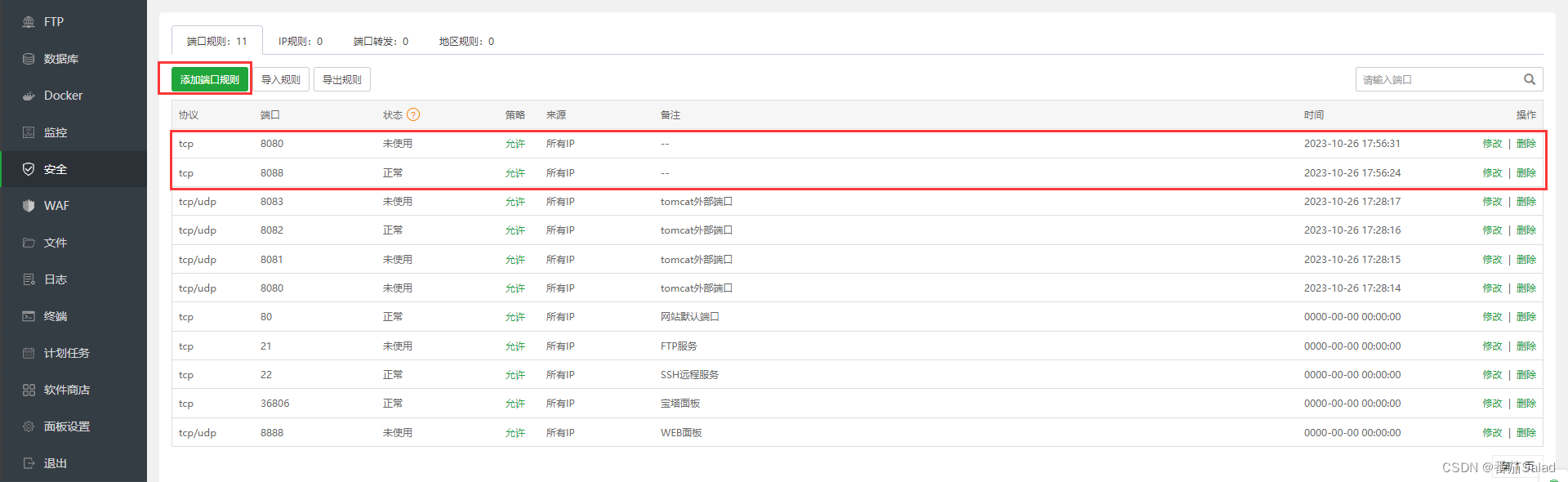
Vue+ElementUI项目打包部署到Ubuntu服务器中
1、修改config/index.js中的assetsPublicPath: /,修改为assetsPublicPath: ./ assetsPublicPath: ./2、在build/utils.js中增加publicPath: ../../ publicPath: ../../3、打开终端,在根目录下执行npm run build进行打包,打包成功后会生成dist npm run…...
)
面试题收集——Java基础部分(一)
1、一个".java"源文件中是否可以包括多个类(不是内部类)?有什么限制? 可以有多个类,但只能有一个public的类,并且public的类名必须与文件名相一致。 2、Java有没有goto? java中的保留字…...

Vue中this指向问题
文章目录 1 由Vue管理的函数2 不被Vue管理的函数3 总结 1 由Vue管理的函数 computed 计算属性watch 监视属性filters (Vue3中已弃用且不再支持) 过滤器methods 上述属性里配置的函数this指向Vue实例,不要采用箭头函数写法,因为箭头函数没有自己的this对…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...
