栈、共享栈、链式栈(C++实现)
文章目录
- 前言
- 1. 栈的顺序存储(顺序栈)
- 2. 栈的基本操作
- 🍑 入栈操作
- 🍑 出栈操作
- 🍑 获取栈顶元素
- 🍑 获取栈的长度
- 🍑 判断是否为空栈
- 🍑 判断栈是否满了
- 🍑 打印栈内的元素
- 🍑 测试函数
- 3. 共享栈
- 🍑 代码实现
- 4. 链式栈
- 🍑 代码实现
- 5. 总结
前言
栈是一种线性表。不过它只能在一端进行插入和删除操作,先入栈的数据只能后出来,而后入栈的数据只能先出来。所以栈具有先进后出或者后进先出的特性。通常来说,我们可以把栈理解为一种 受限的线性表。
如果我们把栈比成一个类似木桶这样的容器,栈有两端,把允许进行插入和删除操作的一端称为 栈顶(top)也就是桶口,或者称为线性表的表尾,而另一端称为 栈底(bottom)也就是桶底,或者称为线性表的表头。不包含任何数据的栈,叫做空栈(空线性表)。
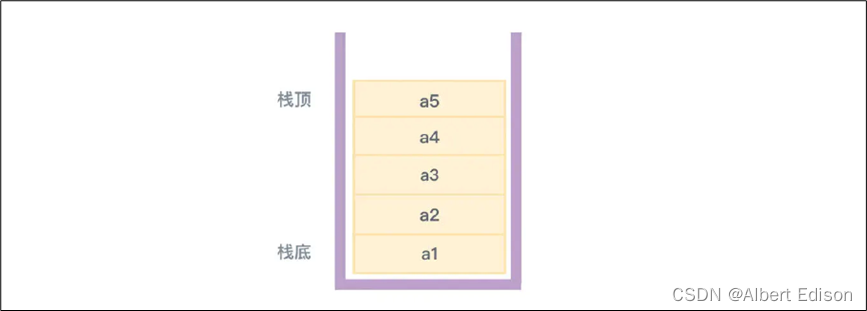
整体结构理清之后,我们再说相关的操作。向栈中插入元素,可以叫做 入栈 或进栈,从栈中删除元素,就叫 出栈。除了能够在表尾插入和删除数据外,对于栈这种数据结构,在任何其他位置插入和删除数据都不应该被允许。你只能提供符合这个规定的操作接口,否则实现的就不是栈了。
栈也被称为 后进先出(Last In First Out:LIFO)的线性表,这意味着最后放入到栈里的数据(插入数据)只能最先被从栈中拿出来(删除数据)。
其实,我们生活中满足栈这种后进先出的情形非常多,比如往抽屉里放东西,先放进去的肯定会被堆到最里面,所以只能最后取出,而最后放入的物品往往在最前面或者最上面,所以会被最先取出。
如果用示意图表示用栈存取数据的过程,就会像下图一样:
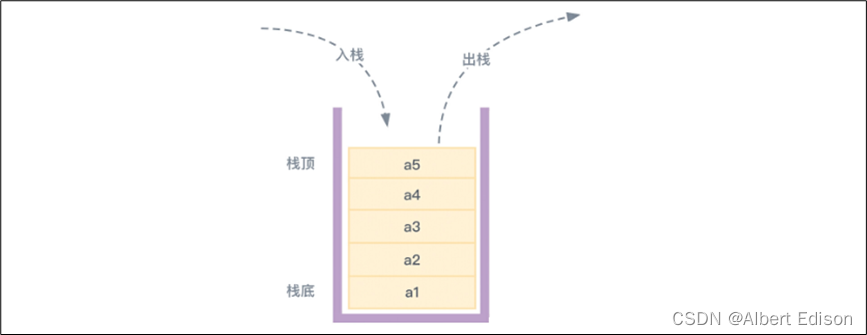
在上图中,如果分别将数据 a1、a2、a3、a4、a5 存入栈中,那么在将数据出栈的时候,顺序就应该是 a5、a4、a3、a2、a1(与入栈顺序正好相反)。
栈是 受限的线性表,比如因为只能在栈顶进行元素的插入和删除操作,所以也无法指定插入和删除操作的位置,所以,栈所支持的操作,可以理解为线性表操作的子集,一般包括栈的创建、入栈(增加数据)、出栈(删除数据)、获取栈顶元素(查找数据)、判断栈是否为空或者是否已满等操作。
1. 栈的顺序存储(顺序栈)
所谓顺序栈,就是顺序存储(用一段连续的内存空间依次存储)栈中的数据。
这里有 2 种保存数据的方案:
- 通过为一维数组 静态 分配内存的方式来保存数据。
- 通过为一维数组 动态 分配内存的方式来保存数据。
为了顺序栈中数据存满时可以对栈进行扩容,在这里,我会采用第 2 种保存数据的方案来编写顺序栈的实现代码。
此外,为了考虑到元素存取的便利性,将数组下标为 0 的一端作为栈底最合适。
2. 栈的基本操作
先进行类定义、初始化以及释放操作。
#define InitSize 10 //动态数组的初始尺寸
#define IncSize 5 //当动态数组存满数据后每次扩容所能多保存的数据元素数量template <typename T>
class SeqStack
{
public:SeqStack(int length = InitSize); //构造函数,参数可以有默认值~SeqStack(); //析构函数public:bool Push(const T& e); //入栈(增加数据)bool Pop(T & e); //出栈(删除数据),也就是删除栈顶数据bool GetTop(T& e); //读取栈顶元素,但该元素并没有出栈而是依旧在栈中void DispList(); //输出顺序栈中的所有元素int ListLength(); //获取顺序栈的长度(实际拥有的元素数量)bool IsEmpty(); //判断顺序栈是否为空bool IsFull(); //判断顺序栈是否已满private:void IncreaseSize(); //当顺序栈存满数据后可以调用此函数为顺序栈扩容private:T* m_data; //存放顺序栈中的元素int m_maxsize; //动态数组最大容量int m_top; //栈顶指针(用作数组下标),指向栈顶元素,该值为-1表示空栈
};//通过构造函数对顺序栈进行初始化
template <typename T>
SeqStack<T>::SeqStack(int length)
{m_data = new T[length]; //为一维数组动态分配内存m_maxsize = length; //顺序栈最多可以存储m_maxsize个数据元素m_top = -1; //空栈
}//通过析构函数对顺序栈进行资源释放
template <typename T>
SeqStack<T>::~SeqStack()
{delete[] m_data;
}
在主函数中,加入代码创建一个初始大小为 10 的顺序栈对象。
int main()
{SeqStack<int> st(10);return 0;
}
创建好以后,那么顺序栈看起来就会是下图的样子,此时是一个空栈:
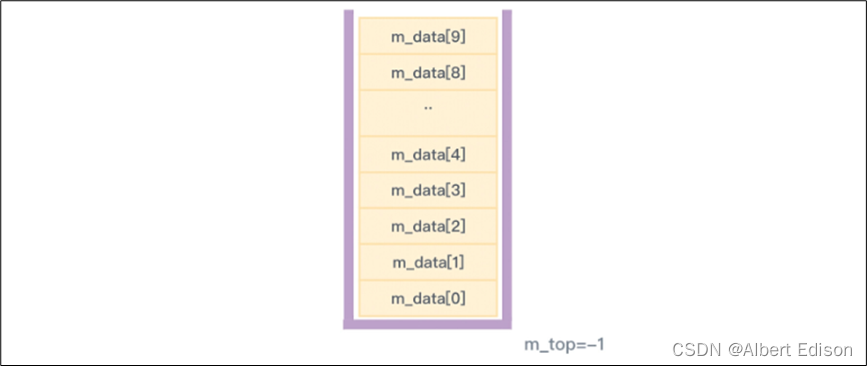
🍑 入栈操作
入栈,增加数据,通常时间复杂度为 O ( 1 ) O(1) O(1),但一旦需要扩容,时间复杂度就会变成 O ( n ) O(n) O(n)了
代码实现
template <typename T>
bool SeqStack<T>::Push(const T& e)
{if (IsFull() == true){IncreaseSize(); //扩容}m_data[++m_top] = e; //存放元素e,栈顶指针向后走return true;
}
当顺序栈存满数据后可以调用此函数为顺序栈扩容,时间复杂度为 O ( n ) O(n) O(n)
template<class T>
void SeqStack<T>::IncreaseSize()
{T* p = m_data;m_data = new T[m_maxsize + IncSize]; //重新为顺序栈分配更大的内存空间 for (int i = 0; i <= m_top; i++){m_data[i] = p[i]; //将数据复制到新区域}m_maxsize = m_maxsize + IncSize; //顺序栈最大长度增加IncSizedelete[] p; //释放原来的内存空间
}
🍑 出栈操作
出栈,删除数据,也就是删除栈顶数据,时间复杂度为 O ( 1 ) O(1) O(1)
template <typename T>
bool SeqStack<T>::Pop(T& e)
{if (IsEmpty() == true){cout << "当前顺序栈为空,不能进行出栈操作!" << endl;return false;}e = m_data[m_top--]; //栈顶元素值返回到e中。return true;
}
🍑 获取栈顶元素
读取栈顶元素,但该元素并没有出栈而是依旧在栈顶中,因此 m_top 值不会发生改变,时间复杂度为 O ( 1 ) O(1) O(1)
代码实现
template <typename T>
bool SeqStack<T>::GetTop(T& e)
{if (IsEmpty() == true){cout << "当前顺序栈为空,不能读取栈顶元素!" << endl;return false;}e = m_data[m_top]; //栈顶元素返回到e中。return true;
}
🍑 获取栈的长度
获取顺序栈的长度(实际拥有的元素数量),时间复杂度为 O ( 1 ) O(1) O(1)
代码实现
template<class T>
int SeqStack<T>::ListLength()
{return m_top + 1;
}
🍑 判断是否为空栈
判断顺序栈是否为空,时间复杂度为 O ( 1 ) O(1) O(1)
代码实现
template<class T>
bool SeqStack<T>::IsEmpty()
{if (m_top == -1){return true;}return false;
}
🍑 判断栈是否满了
判断顺序栈是否已满,时间复杂度为 O ( 1 ) O(1) O(1)
代码实现
template<class T>
bool SeqStack<T>::IsFull()
{if (m_top >= m_maxsize - 1){return true;}return false;
}
🍑 打印栈内的元素
输出顺序栈中的所有元素,时间复杂度为 O ( n ) O(n) O(n)
代码实现
template<class T>
void SeqStack<T>::DispList()
{//按照从栈顶到栈底的顺序来显示数据for (int i = m_top; i >= 0; --i){cout << m_data[i] << " "; //每个数据之间以空格分隔}cout << endl; //换行
}
🍑 测试函数
在主函数中,增加测试代码。
代码实现
int main()
{SeqStack<int> st(10);//入栈 st.Push(10); st.Push(20); st.Push(30); st.Push(40); st.Push(50); //打印st.DispList(); //获取栈顶元素int elem = 0;st.GetTop(elem);cout << elem << endl; //出栈 st.Pop(elem);st.Pop(elem);//打印st.DispList(); return 0;
}
运行结果如下:
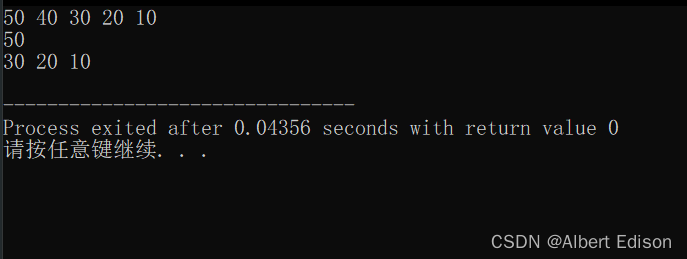
在有的实现栈的代码中,会让 m_top 的初始值等于 0(指向 0 的位置),那么判断栈是否为空的代码(IsEmpty 函数)也就是判断 m_top 是否等于 0,而判断栈满(IsFull 函数)的条件也应该变成 if (m_top >= m_maxsize)。
这种实现方式,实际就是让 m_top 代表下一个可以放入栈中的元素的下标,当数据入栈(Push 函数)时,代码行 m_top++ 和代码行 m_data[m_top] = e 的执行就需要互换顺序,而当数据出栈(Pop 函数)时,代码行 e = m_data[m_top] 和代码行 m_top-- 的执行也需要互换顺序。
3. 共享栈
所谓共享栈,就是两个顺序栈共享存储空间。为什么会提出这个概念呢?
之前我们提到的顺序栈,一个比较大的缺点是保存数据的空间初始尺寸不好确定,如果太大,就会浪费空间,如果太小,那么存满数据后再入栈新数据就需要扩容,而扩容就又需要开辟一整块更大的新区域并将原有数据复制到新区域,操作起来比较耗费性能。
不过,我们可以设想一下。假设有两个相同数据类型的顺序栈,如果分别为他们开辟了保存数据的空间,那是不是就可能出现,第一个栈的数据已经存满了而另一个栈中还有很多存储空间的情形呢?那么,如果开辟出来一块保存数据的空间后,让这两个栈同时使用,也就是共享这块空间,是不是也许就能达到最大限度利用这块空间、减少浪费的目的呢?这就是共享栈的含义。
下面直接给出共享栈的实现代码。
🍑 代码实现
代码实现
//共享栈
template <typename T> //T代表数组中元素的类型
class ShareStack
{
public:ShareStack(int length = InitSize) //构造函数,参数可以有默认值{m_data = new T[length]; //为一维数组动态分配内存m_maxsize = length; //共享栈最多可以存储m_maxsize个数据元素m_top1 = -1; //顺序栈1的栈顶指针为-1,表示空栈m_top2 = length; //顺序栈2的栈顶指针为length,表示空栈}~ShareStack() //析构函数{delete[] m_data;}public:bool IsFull() //判断共享栈是否已满{if (m_top1 + 1 == m_top2){return true;}return false;}bool Push(int stackNum, const T& e) //入栈(增加数据),参数stackNum用于标识栈1还是栈2{if (IsFull() == true){//共享栈满了,你也可以自行增加代码来支持动态增加共享栈的容量,这里简单处理,直接返回falsecout << "共享栈已满,不能再进行入栈操作了!" << endl;return false;}if (stackNum == 1){//要入的是顺序栈1m_top1++; //栈顶指针向后走m_data[m_top1] = e;}else{//要入的是顺序栈2m_top2--;m_data[m_top2] = e;}return true;}bool Pop(int stackNum, T& e) //出栈(删除数据),也就是删除栈顶数据{if (stackNum == 1){//要从顺序栈1出栈if (m_top1 == -1){cout << "当前顺序栈1为空,不能进行出栈操作!" << endl;return false;}e = m_data[m_top1]; //栈顶元素值返回到e中m_top1--;}else{//要从顺序栈2出栈if (m_top2 == m_maxsize){cout << "当前顺序栈2为空,不能进行出栈操作!" << endl;return false;}e = m_data[m_top2];m_top2++;}return true;}private:T* m_data; //存放共享栈中的元素int m_maxsize; //动态数组最大容量int m_top1; //顺序栈1的栈顶指针int m_top2; //顺序栈2的栈顶指针
};
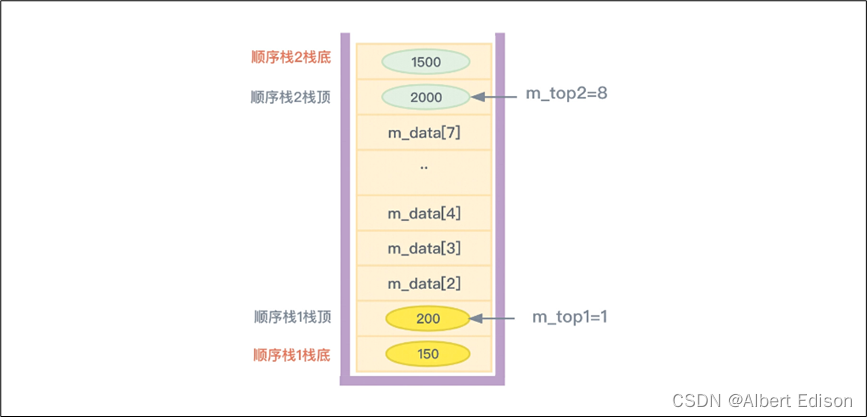
从代码中可以看到,既然是两个顺序栈共享同一块内存空间,那么就需要引入两个栈顶指针(m_top1、m_top2)来分别标识这两个顺序栈的栈顶位置。顺序栈 1 的栈底位置在最下面,而顺序栈 2 的栈底位置在最上面。
同时,注意阅读判断共享栈是否已满的代码(IsFull)以及入栈和出栈(Push、Pop)的代码。如果对顺序栈 1 进行入栈操作,则 m_top1 要递增,数据要从下向上存储。如果对顺序栈 2 进行入栈操作,则 m_top2 要递减,数据从上向下存储。
这样的话,从逻辑上看,实现的是两个栈,但这两个栈又是共享着同一块物理内存的,从而提高内存利用率。如下图所示:
4. 链式栈
链式栈,就是链式存储方式来实现的栈。我们知道单链表的插入操作 ListInsert 方法,其第一个参数用于指定元素要插入的位置,如果把该参数值设置为 1,就是链式栈的入栈操作。对于单链表的删除操作 ListDelete 方法,其参数用于指定要删除的元素位置,如果把该参数值也设置为 1,就是链式栈的出栈操作。
可以发现,链式栈其实就是一个单链表,只不过人为的规定只能在单链表的第一个位置进行插入(入栈)和删除(出栈)操作,即链表头这一端是栈顶。
链式栈的实现代码和单链表的实现代码非常类似,可以把链式栈理解成受限的单链表。但对于链式栈来讲,考虑到只在链表头位置插入数据,所以链式栈一般不需要带头节点。
🍑 代码实现
代码实现
//链式栈中每个节点的定义
template <typename T> //T代表数据元素的类型
struct StackNode
{T data; //数据域,存放数据元素StackNode<T>* next; //指针域,指向下一个同类型(和本节点类型相同)节点
};//链式栈的定义
template <typename T>
class LinkStack
{
public:LinkStack(); //构造函数~LinkStack(); //析构函数public:bool Push(const T& e); //入栈元素ebool Pop(T& e); //出栈(删除数据),也就是删除栈顶数据bool GetTop(T& e); //读取栈顶元素,但该元素并没有出栈而是依旧在栈中void DispList(); //输出链式栈中的所有元素int ListLength(); //获取链式栈的长度bool Empty(); //判断链式栈是否为空private:StackNode<T>* m_top; //栈顶指针int m_length; //链式栈当前长度
};//通过构造函数对链式栈进行初始化
template <typename T>
LinkStack<T>::LinkStack()
{m_top = nullptr;m_length = 0;
}//通过析构函数对链式栈进行资源释放
template <typename T>
LinkStack<T>::~LinkStack()
{T tmpnousevalue = { 0 };while (Pop(tmpnousevalue) == true) {} //把栈顶元素删光,while循环也就退出了,此时也就是空栈了
}//入栈元素e,时间复杂度为O(1)
template <typename T>
bool LinkStack<T>::Push(const T& e)
{StackNode<T>* node = new StackNode<T>;node->data = e;node->next = m_top;m_top = node;m_length++;return true;
}//出栈(删除数据),也就是删除栈顶数据,时间复杂度为O(1)
template <typename T>
bool LinkStack<T>::Pop(T& e)
{if (Empty() == true) //链式栈为空return false;StackNode<T>* p_willdel = m_top;m_top = m_top->next;m_length--;e = p_willdel->data;delete p_willdel;return true;
}//读取栈顶元素,但该元素并没有出栈而是依旧在栈中
template <typename T>
bool LinkStack<T>::GetTop(T& e)
{if (Empty() == true) //链式栈为空return false;e = m_top->data;return true;
}//输出链式栈中的所有元素,时间复杂度为O(n)
template<class T>
void LinkStack<T>::DispList()
{if (Empty() == true) //链式栈为空return;StackNode<T>* p = m_top;while (p != nullptr){cout << p->data << " "; //每个数据之间以空格分隔p = p->next;}cout << endl; //换行
}//获取链式栈的长度,时间复杂度为O(1)
template<class T>
int LinkStack<T>::ListLength()
{return m_length;
}//判断链式栈是否为空,时间复杂度为O(1)
template<class T>
bool LinkStack<T>::Empty()
{if (m_top == nullptr) //链式栈为空{return true;}return false;
}
与顺序栈相比,链式栈没有长度限制,不存在内存空间的浪费问题。但对于数据的入栈和出栈这些需要对数据进行定位的操作,顺序栈更加方便,而链式栈中的每个数据节点都需要额外的指针域以指向下一个数据节点,这会略微降低数据的存储效率,当然也会多占用一些内存。
所以,如果要存储的数据数量无法提前预估,一般考虑使用链式栈,而如果数据的数量比较固定,可以考虑使用顺序栈。
5. 总结
顺序栈可以看成是功能受限的数组,或把链式栈看成是功能受限的单链表,都是没有问题的。为什么创造出功能受限的栈来呢?你可以理解为,因为功能受限,所以使用起来也更加简单,错用误用的概率比数组、单链表等更低。
栈有很多应用,比如:在函数调用期间需要用栈来保存临时的参数信息、函数内局部变量信息、函数调用返回地址信息等。网上也有很多小例子演示栈的简单应用,比如利用栈来进行括号匹配的检验,利用栈来计算表达式结果等。以及用栈来实现诸如树的非递归遍历、记录节点路径信息等操作。
相关文章:

栈、共享栈、链式栈(C++实现)
文章目录 前言1. 栈的顺序存储(顺序栈)2. 栈的基本操作🍑 入栈操作🍑 出栈操作🍑 获取栈顶元素🍑 获取栈的长度🍑 判断是否为空栈🍑 判断栈是否满了🍑 打印栈内的元素&am…...
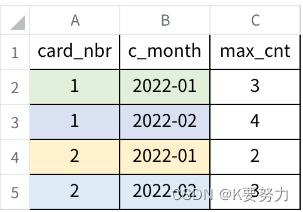
MySQL实战2
文章目录 主要内容一.回访用户1.准备工作代码如下(示例): 2.目标3.实现代码如下(示例): 二.如何找到每个人每月消费的最大天数1.准备工作代码如下(示例): 2.目标3.实现代码如下(示例)…...

【面试经典150 | 栈】简化路径
文章目录 Tag题目来源题目解读解题思路方法一:字符串数组模拟栈 其他语言python3 写在最后 Tag 【栈】【字符串】 题目来源 71. 简化路径 题目解读 将 Unix 风格的绝对路径转化成更加简洁的规范路径。字符串中会出现 字母、数字、/、_、. 和 .. 这几种字符&#…...
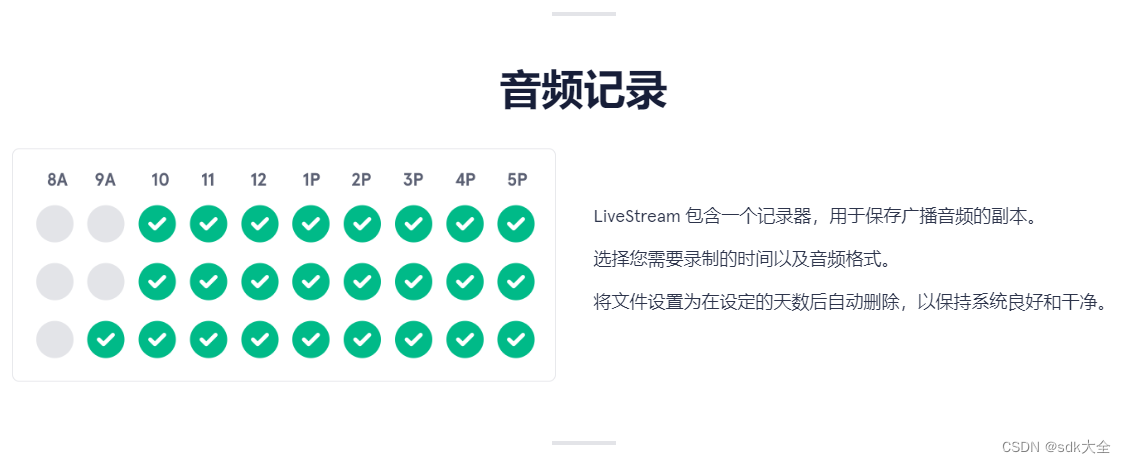
无线电编码和记录和静音检测器 PlayOutONE LiveStream 5.0
直播编码器,随处流式传输。LiveStream 应用程序的多色图案屏幕截图,显示一波进入,四路流出来,LiveStream是一站式应用程序,可让您的电台在需要的地方输出。 对音频进行编码以进行流式传输,使用您最喜欢的V…...

React中useEffect Hook使用纠错
引言 React是一种流行的JavaScript库,用于构建用户界面。它提供了许多强大的功能和工具,使开发人员能够轻松地构建交互式和可重用的组件。其中一个最常用的功能是React的useEffect Hook,它允许我们在函数组件中执行副作用操作。然而…...

0049【Edabit ★☆☆☆☆☆】【修改Bug代码】Buggy Code
0049【Edabit ★☆☆☆☆☆】【修改Bug代码】Buggy Code bugs language_fundamentals Instructions The challenge is to try and fix this buggy code, given the inputs true and false. See the examples below for the expected output. Examples has_bugs(true) // &qu…...
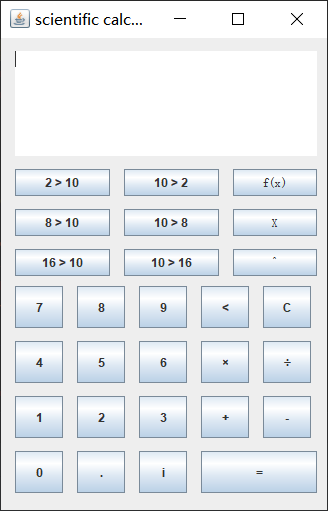
javaswing/gui的科学计算器
一个使用javajavaswing/gui的科学计算器程序。 支持加减乘除,函数运算,清空,退回等操作。 还支持进制运算。 源码下载地址 支持:远程部署/安装/调试、讲解、二次开发/修改/定制...

Chapter1:C++概述
此专栏为移动机器人知识体系的 C {\rm C} C基础,基于《深入浅出 C {\rm C} C》(马晓锐)的笔记, g i t e e {\rm gitee} gitee链接: 移动机器人知识体系. 1.C概述 1.1 C概述 计算机系统分为硬件系统和软件系统。 硬件系统:指组成计算机的电子…...
实战经验分享FastAPI 是什么
FastAPI 是什么?FastAPI实战经验分享  FastAPI 是一个先进、高效的 Python Web 框架,专门用于构建基于 Python 的 API。它是…...

Edge浏览器中常用的20个快捷键
Microsoft Edge,和许多其他网络浏览器一样,设有一系列的键盘快捷方式,旨在提高用户效率。以下是Edge浏览器的20个实用快捷键: Ctrl T - 打开一个新标签页。Ctrl W(或 Ctrl F4)- 关闭当前标签页。Ctrl …...
winscp显示隐藏文件
当前目录下有被隐藏的文件时,会在右下角看到 “已隐藏” 的字样,双击这个字样,就会显示被隐藏的文件和文件夹...

uniapp获取地理位置的API是什么?
UniApp获取地理位置的API是uni.getLocation。它的作用是获取用户的当前地理位置信息,包括经纬度、速度、高度等。通过该API,开发者能够实现基于地理位置的功能,如显示用户所在位置附近的商家、导航服务、天气查询等。 以下是一个示例&#x…...

【ARMv8 SIMD和浮点指令编程】NEON 通用数据处理指令——复制、反转、提取、转置...
NEON 通用数据处理指令包括以下指令(不限于): • DUP 将标量复制到向量的所有向量线。 • EXT 提取。 • REV16、REV32、REV64 反转向量中的元素。 • TBL、TBX 向量表查找。 • TRN 向量转置。 • UZP、ZIP 向量交叉存取和反向交叉存取。 1 DUP (element) 将…...
C#,数值计算——分类与推理,基座向量机的 Svmgenkernel的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { public abstract class Svmgenkernel { public int m { get; set; } public int kcalls { get; set; } public double[,] ker { get; set; } public double[] y { get; set…...
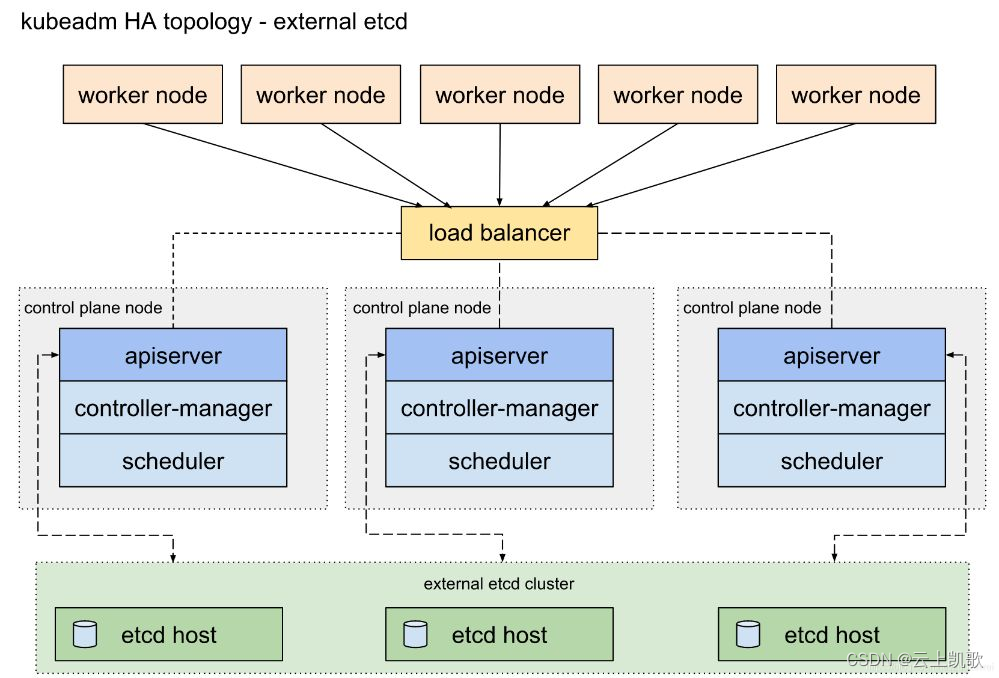
08.K8S高可用方案
K8S高可用方案 1、高可用部署方式 官方提供两种高可用实现方式: 堆叠etcd 拓扑,其中 etcd 节点与控制平面节点共存;外部 etcd 节点,其中 etcd 与控制平面在不同的节点上运行;1.1、堆叠 etcd 拓扑 主要特点: 每个 master 节点上运行一个 apiserver 和 etcd, etcd 只与本…...
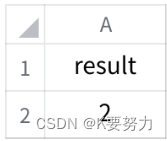
MySQL实战1
文章目录 主要内容一.墨西哥和美国第三高峰1.准备工作代码如下(示例): 2.目标3.实现代码如下(示例): 4.相似例子代码如下(示例): 二.用latest_event查找当前打开的页数1.准备工作代码如下(示例&…...

关于A level的习题答案
CAIE考试局(也称为CIE) 的真题答案有本书叫做《A-level 数学历年真题全解》包含2015-2019的Paper1、Paper3、Paper4、Paper6 Further Mathematica cousebook这本书的最后有Answer但是没有过程 Edexcel考试局 书本末尾有简易答案。 但是具体答案在Sol…...

左神算法题系列:动态规划机器人走路
机器人走路 假设有排成一行的N个位置记为1~N,N一定大于或等于2 开始时机器人在其中的start位置上(start一定是1~N中的一个) 如果机器人来到1位置,那么下一步只能往右来到2位置; 如果机器人来到N位置,那么下一步只能往左来到N-1位…...

LeetCode75——Day19
文章目录 一、题目二、题解 一、题目 724. Find Pivot Index Given an array of integers nums, calculate the pivot index of this array. The pivot index is the index where the sum of all the numbers strictly to the left of the index is equal to the sum of all…...
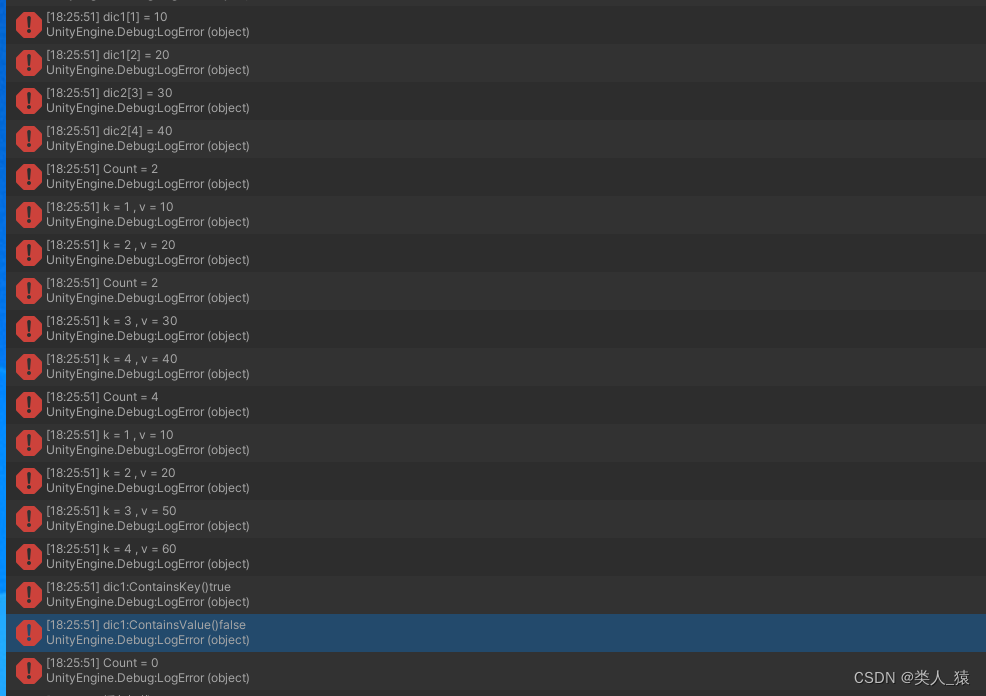
ToLua使用原生C#List和Dictionary
ToLua是使用原生C#List 介绍Lua中使用原生ListC#调用luaLua中操作打印测试如下 Lua中使用原生DictionaryC#调用luaLua中操作打印测试如下 介绍 当你用ToLua时C#和Lua之间肯定是会互相调用的,那么lua里面使用List和Dictionary肯定是必然的,在C#中可以调用…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
