C语言:杨氏矩阵、杨氏三角、单身狗1与单身狗2
下面介绍四道题目和解法
1.杨氏矩阵
算法:右上角计算
题目:有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。
要求:时间复杂度小于O(N);
代码:
#include<stdio.h>
int Find_arr(int arr[3][3],int r, int c, int k)
{int x = 0;int y = c - 1;while (x<r&&y>=0){if (arr[x][y] < k){x++;}else if (arr[x][y] > k){y--;}elsereturn 1;}return 0;
}int main()
{int arr[3][3] = {1,2,3,4,5,6,7,8,9};int k = 0;printf("输入需要查找的数字:");scanf("%d",&k);int ret = 0;ret=Find_arr(arr,3,3,k);if (ret == 1)printf("找到了\n");elseprintf("找不到\n");return 0;
}【关键代码部分解析】
杨氏矩阵的特点:矩阵的每行从左到右是递增的,矩阵从上到下是递增的
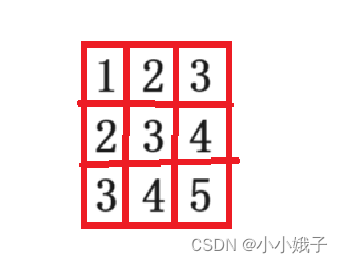
代码思路:从右上角或者左下角开始遍历,我们这里从右上角开始
假设要找的值是5
第一次遍历:与右上角的元素比较,也就是与3比较。
第二次遍历:与4比较。
第三次遍历:与5比较,相等,得出结果。
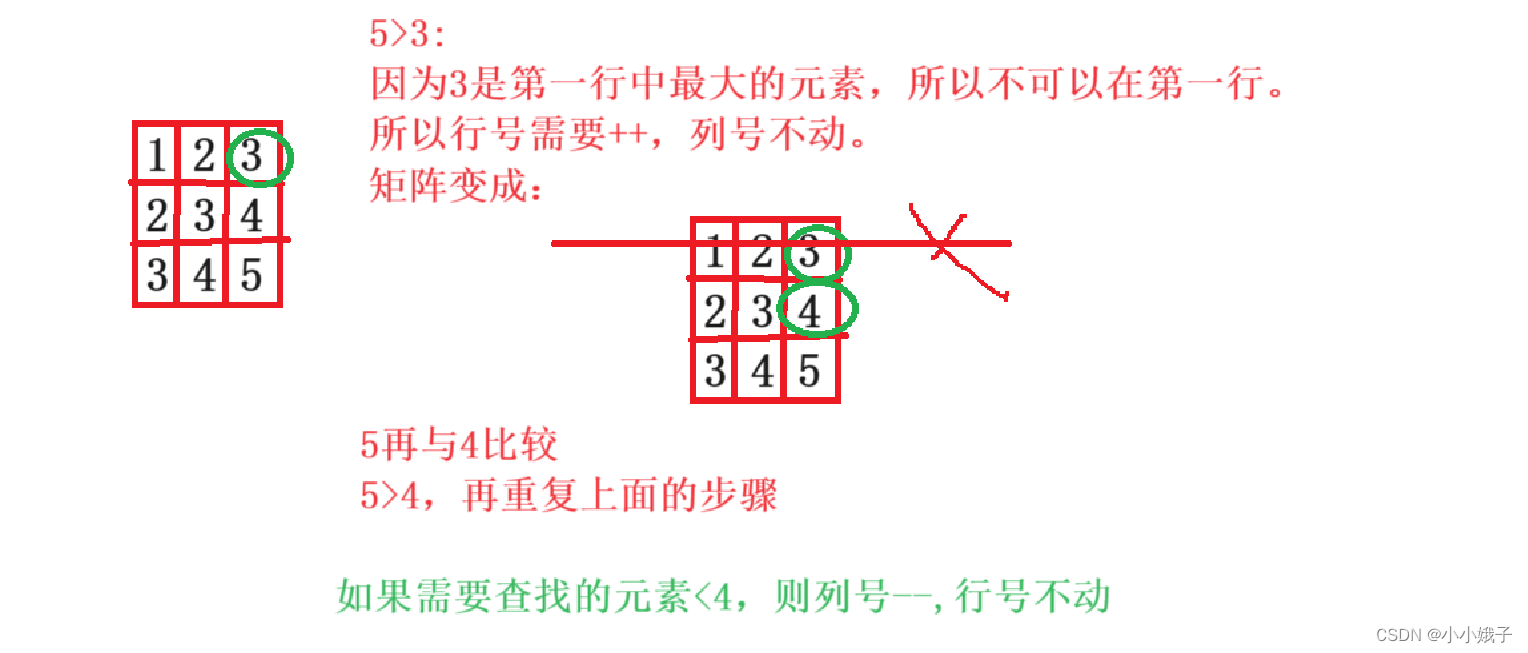
【第二种代码】
要求找到了并且返回该元素的下标:
返回双参数代码写法:
#include<stdio.h>
#include<assert.h>
int Find_arr(int arr[3][3], int* px, int* py, int k)
{assert(px&&py);int x = 0;int y = *py-1;while (x<*px&&*py>=0){if (arr[x][y] < k){x++;}else if (arr[x][y] > k){y--;}else{*px = x;*py = y;return 1;}}*px = -1;*py = -1;return 0;
}int main()
{int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };int k = 0;printf("输入需要查找的数字:");scanf("%d", &k);int ret = 0;int x = 3;int y = 3;ret = Find_arr(arr, &x,&y, k);if (ret == 1){printf("找到了\n");printf("下标是:%d %d\n", x, y);}else{printf("找不到\n");printf("下标是:%d %d\n", x, y);}return 0;
}返回双参数思路:
将下标的地址作为参数,不需要返回两个下标即可达到带回参数的目的。
2.杨辉三角
我们想要打印出下面的图案,并且符号性质,需要怎么做呢?

(1)图形讲解
我们可以创建一个二维数组,刚开始都赋值0。
然后可以打印出下半部分就行。
代码:
#include<stdio.h>
int main()
{int arr[10][10] = { 0 };//创建二维数组并初始化成0//打印下半部分int i = 0;for (i=0;i<10;i++){int j = 0;for (j=0;j<=i;j++)//打印三角形的关键{printf("%d ",arr[i][j]);}printf("\n");}return 0;
}运行结果:
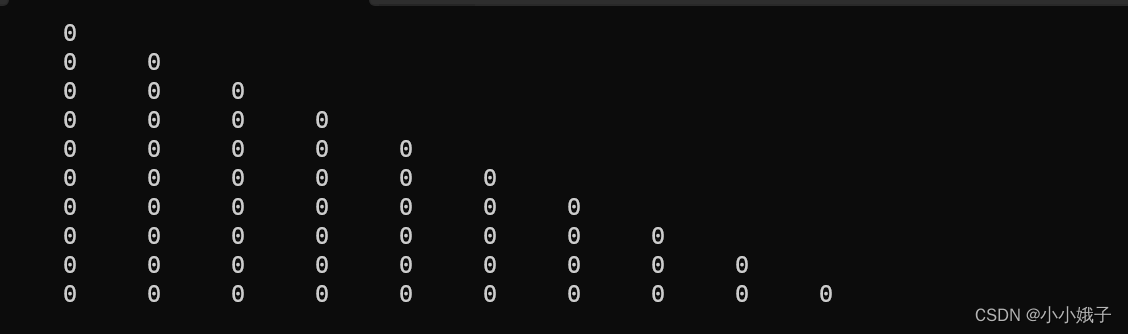
(2)赋值讲解
现在知道了杨辉三角的形状是怎么样打印出来的,接下来需要对其赋值,成为真正的杨辉三角。
杨辉三角:从第三行和第二列开始,每个数字的值=其上方的数字+左上角的数字 (空白的默认为0),其他部分默认赋值1。
代码:
#include<stdio.h>
int main()
{int arr[10][10] = { 0 };//创建二维数组并初始化成0//对杨辉三角赋值(二维数组)int i = 0;for (i = 0; i < 10; i++){int j = 0;for (j = 0; j <= i; j++){if (j == 0 || i == j)arr[i][j] = 1;if (i >= 2 && j >= 1)//第三行和第二列开始//关系arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];}}//打印下半部分i = 0;for (i=0;i<10;i++){int j = 0;for (j=0;j<=i;j++)//打印三角形的关键{printf("%5d ",arr[i][j]);}printf("\n");}return 0;
}运行结果:
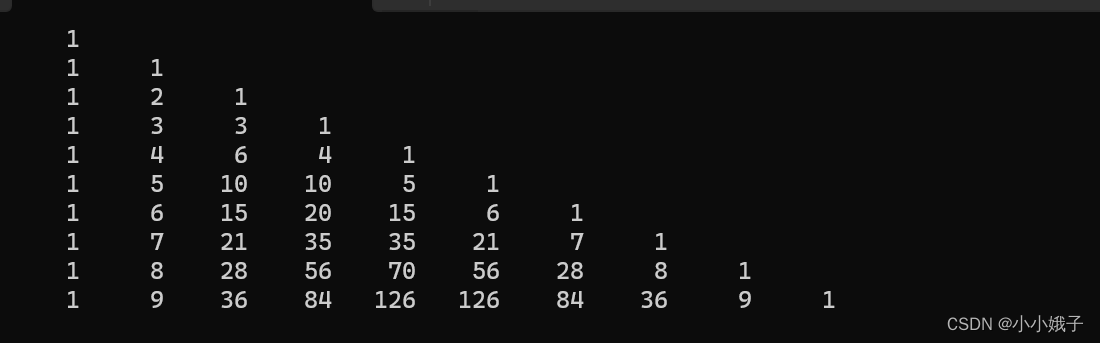
赋值解析:
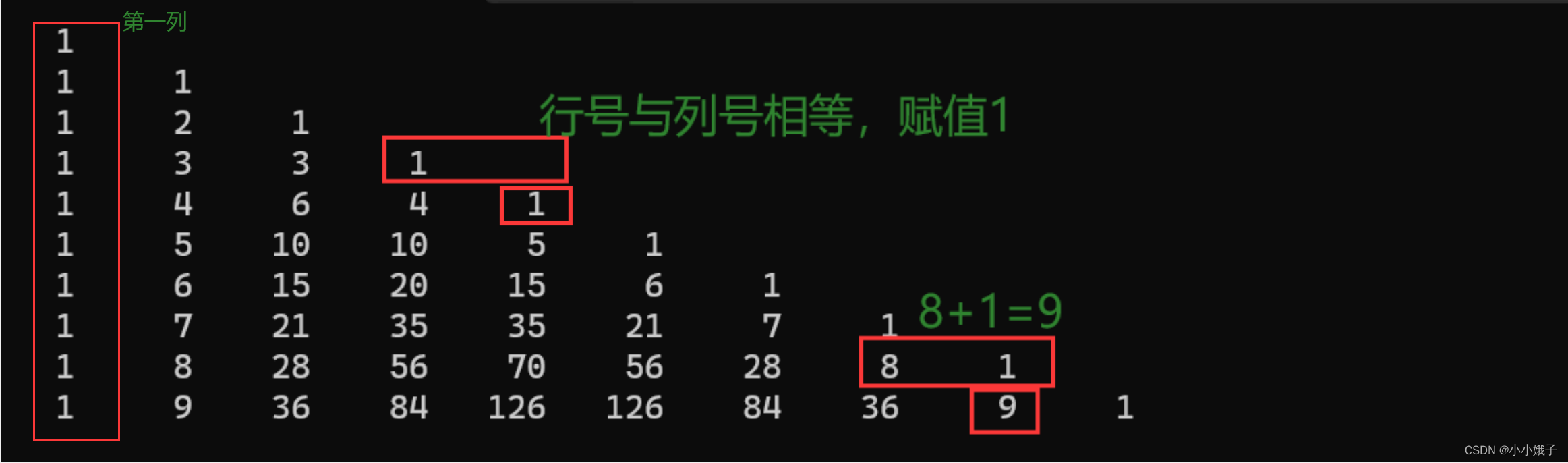
其实这就是杨辉三角了,要是打出类似等腰三角形的性质,则需要控制打印的格式,属于打印的知识,这里暂时不介绍
等腰三角的杨辉三角:暂时不做解析
#include<stdio.h>int main()
{int arr[10][10] = { 0 };//初始化int i = 0;for (i = 0; i < 10; i++){int j = 0;for (j = 0; j <= i; j++){if (j == 0 || i == j)arr[i][j] = 1;if (i >= 2 && j >= 1)//第三行和第二列开始arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];}}//打印i = 0;int k = 10;for (i = 0; i < 10; i++){for (int k = 0; k < 26 - (6 * i / 2); k++)//打印一行前面的空格{printf(" ");}int j = 0;for (j = 0; j <= i; j++){printf("%5d ", arr[i][j]);}printf("\n");}return 0;
}
运行结果:
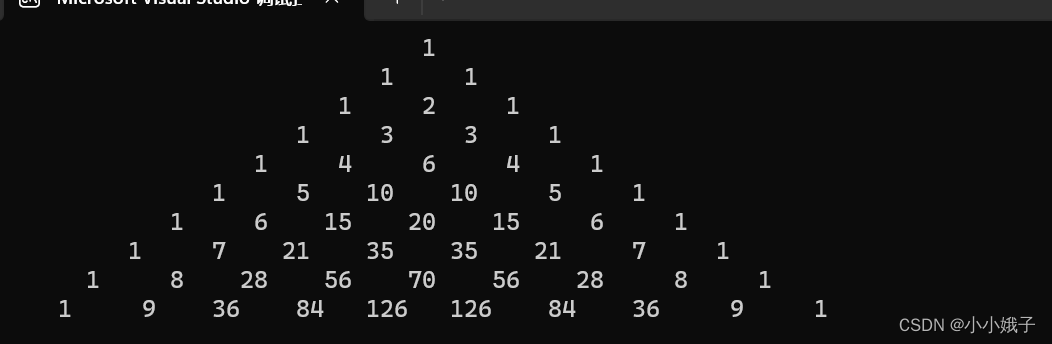
3.单身狗1
题目:一个数组中只有一个数字单独出现,其他的数字都成对出现,请找出这个单身狗
如:1,2,3,4,5,1,2,3,4,只有5只出现了一次,所以需要找出5
【思路】
(1)利用异或操作符^:(二进制对应位)相同为0,相异为1。
(2)如:a^a=0,a^0=0。
(3)并且支持交换律,所以我们可以将所有的数据和0异或在一起,最终的结果就是“单身狗”。
代码解法:
#include<stdio.h>
int Find_dog_arr(int arr[],int sz)
{int tmp = 0;int i = 0;for (i = 0; i < sz; i++){tmp = tmp ^ arr[i];//全部异或在一起}return tmp;
}
int main()
{int arr[] = { 1,2,3,4,5,1,2,3,4 };int sz = sizeof(arr) / sizeof(arr[0]);int ret=Find_dog_arr(arr,sz);printf("%d\n",ret);return 0;
}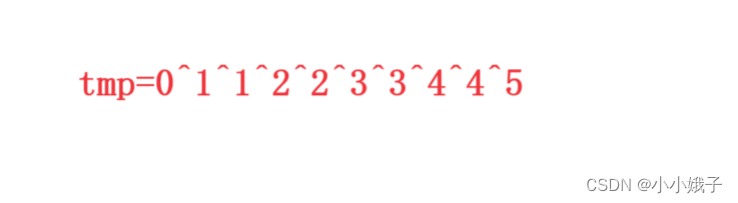
tmp的最终结果就是5。
4.单身狗2
题目:
一个数组中只有两个数字是出现一次,其他所有数字都出现了两次。
编写一个函数找出这两个只出现一次的数字。
例如:
有数组的元素是:1,2,3,4,5,1,2,3,4,6
只有5和6只出现1次,要找出5和6。
【思路】
(1)这是单身狗1的升级版,显然直接异或是不行的。
(2)所以我们可以先进行分类,将两个单身狗分在两个不同的组,再进行异或操作。
(3)怎么分类:找出分类依据。
利用异或操作分类,将所有数字异或起来的结果其实就是两个单身狗异或起来的结果;再根据结果的二进制,也就是根据某一位二进制是否为1进行分类。(两个单身狗肯定有不同的二进制位,结果肯定为1)
【分类操作】
void Find_dog2_arr(int arr[], int sz, int* p1, int* p2)
{int tmp = 0;int i = 0;//1.全部异或在一起,结果为两个单身狗异或在一起的结果for (i = 0; i < sz; i++){tmp ^= arr[i];}//2.找出分组的依据i = 0;int r = 0;for (i = 0; i < 32; i++){r = arr[i];if ((tmp >> i) & 1 == 1){r = i;}}
}(1)tmp是两个单身狗异或在一起的结果
(2)(tmp>>i)&1==1的意思是找出tmp的二进制位为1的位,也就是分组的关键
【思路刨析】

【整体代码】
#include<stdio.h>
void Find_dog2_arr(int arr[], int sz, int* p1, int* p2)
{int tmp = 0;int i = 0;//1.全部异或在一起,结果为两个单身狗异或在一起的结果for (i = 0; i < sz; i++){tmp ^= arr[i];}//2.找出分组的依据i = 0;int r = 0;for (i = 0; i < 32; i++){r = arr[i];if ((tmp >> i) & 1 == 1){r = i;}}//3.分组int u1 = 0;int u2 = 0;for (i = 0; i < sz; i++){if ((arr[i] >> r) & 1 == 1)//按位与{u1 ^= arr[i];}else{u2 ^= arr[i];}}*p1 = u1;*p2 = u2;
}
int main()
{int arr[] = { 1,2,3,4,5,1,2,3,4,10 };int sz = sizeof(arr) / sizeof(arr[0]);int s1 = 0;int s2 = 0;Find_dog2_arr(arr, sz, &s1, &s2);printf("单身狗1:%d\n单身狗2:%d", s1, s2);return 0;
}
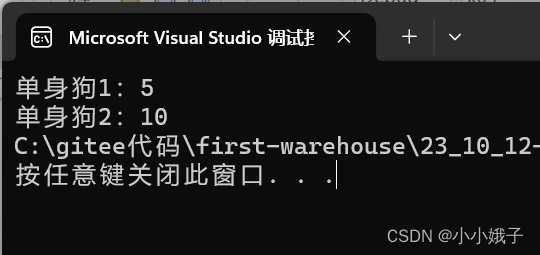
相关文章:

C语言:杨氏矩阵、杨氏三角、单身狗1与单身狗2
下面介绍四道题目和解法 1.杨氏矩阵 算法:右上角计算 题目:有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。 要求:时间复杂度小于O(N…...

PX4天大bug,上电反复重启,连不上QGC!
一、Debug与Bug 由于自己写的代码CPU占用率过高,解锁报错 CPU load too high!无法解锁。 于是把 COM_CPU_MAX 从默认的 90% 变为 99%(千万别这样搞,这是bug,除非想玩!)。 然后重启,飞机就反…...
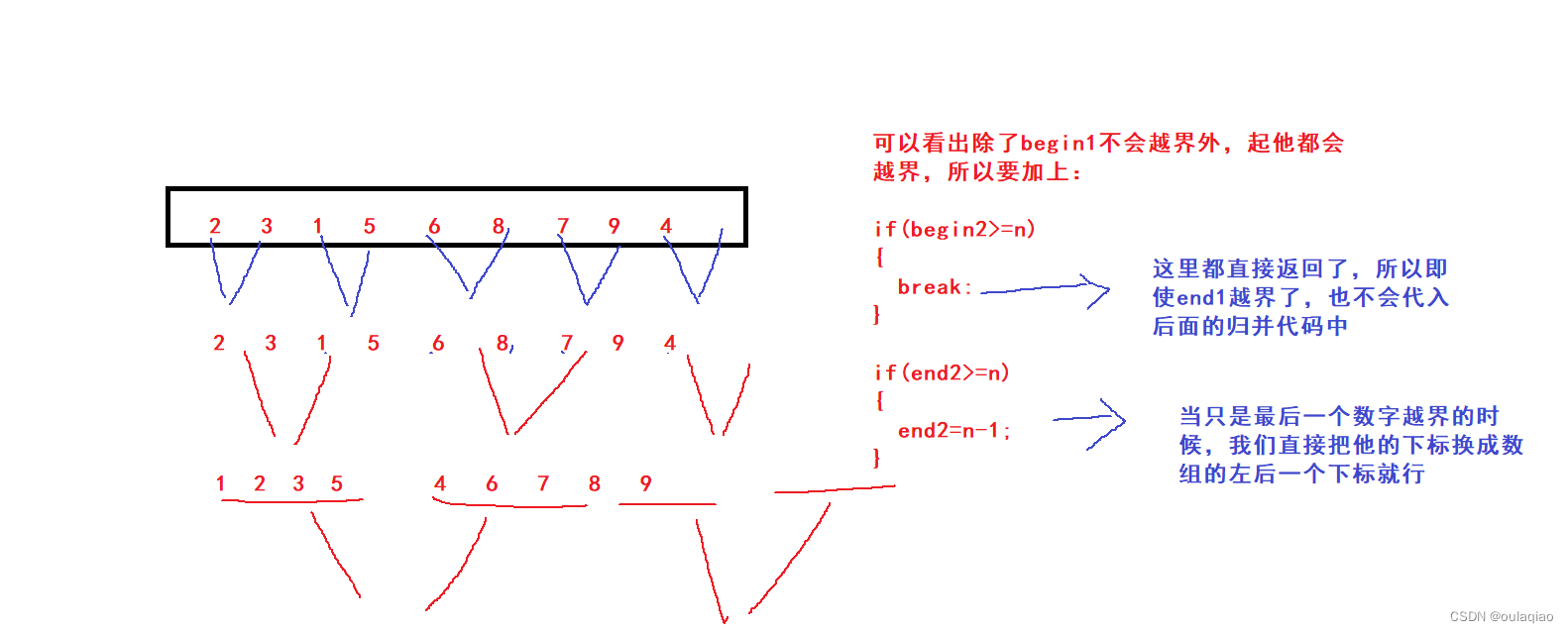
归并排序——
之前我们学习过把两个有序数组合并再一起后任然有序,就叫归并; 那么,排序是否也可以把一个要排序的数组分割成两个有序的数组,然后归并,之后再拷贝回原数组,就实现了排序 但是怎么才能控制分割成的数组是有…...
阿里云企业邮箱基于Spring Boot快速实现发送邮件功能
邮件在项目中经常会被用到,比如用邮件发送通知。比如,通过邮件注册、认证、找回密码、系统报警通知、报表信息等。本篇文章带大家通过SpringBoot快速实现一个发送邮件的功能。 邮件协议 下面先简单了解一下常见的邮件协议。常用的电子邮件协议有SMTP、…...

大数据Doris(十三):创建用户和创建数据库并赋予权限
文章目录 创建用户和创建数据库并赋予权限 一、创建用户...

【Unity小技巧】可靠的相机抖动及如何同时处理多个震动
文章目录 每篇一句前言安装虚拟相机虚拟相机震动测试代码控制震动清除震动控制震动的幅度和时间 两个不同的强弱震动同时发生源码完结 每篇一句 围在城里的人想逃出来,站在城外的人想冲进去,婚姻也罢,事业也罢,人生的欲望大都如此…...

Megatron-LM GPT 源码分析(四) Virtual Pipeline Parallel分析
引言 本文接着上一篇【Megatron-LM GPT 源码分析(三) Pipeline Parallel分析】,基于开源代码 GitHub - NVIDIA/Megatron-LM: Ongoing research training transformer models at scale ,通过GPT的模型运行示例,从三个维…...

IOC课程整理-8 Spring Bean作用域
1 Spring Bean作用域 2" singleton " Bean作用域 3" prototype " Bean作用域 • 注意事项 • Spring 容器没有办法管理 prototype Bean 的完整生命周期,也没有办法记录实例的存在。销毁回调方法将不会执行,可以利用 BeanPostProces…...

本地websocket服务端暴露至公网访问【内网穿透】
本地websocket服务端暴露至公网访问【cpolar内网穿透】 文章目录 本地websocket服务端暴露至公网访问【cpolar内网穿透】1. Java 服务端demo环境2. 在pom文件引入第三包封装的netty框架maven坐标3. 创建服务端,以接口模式调用,方便外部调用4. 启动服务,出现以下信息表示启动成功…...
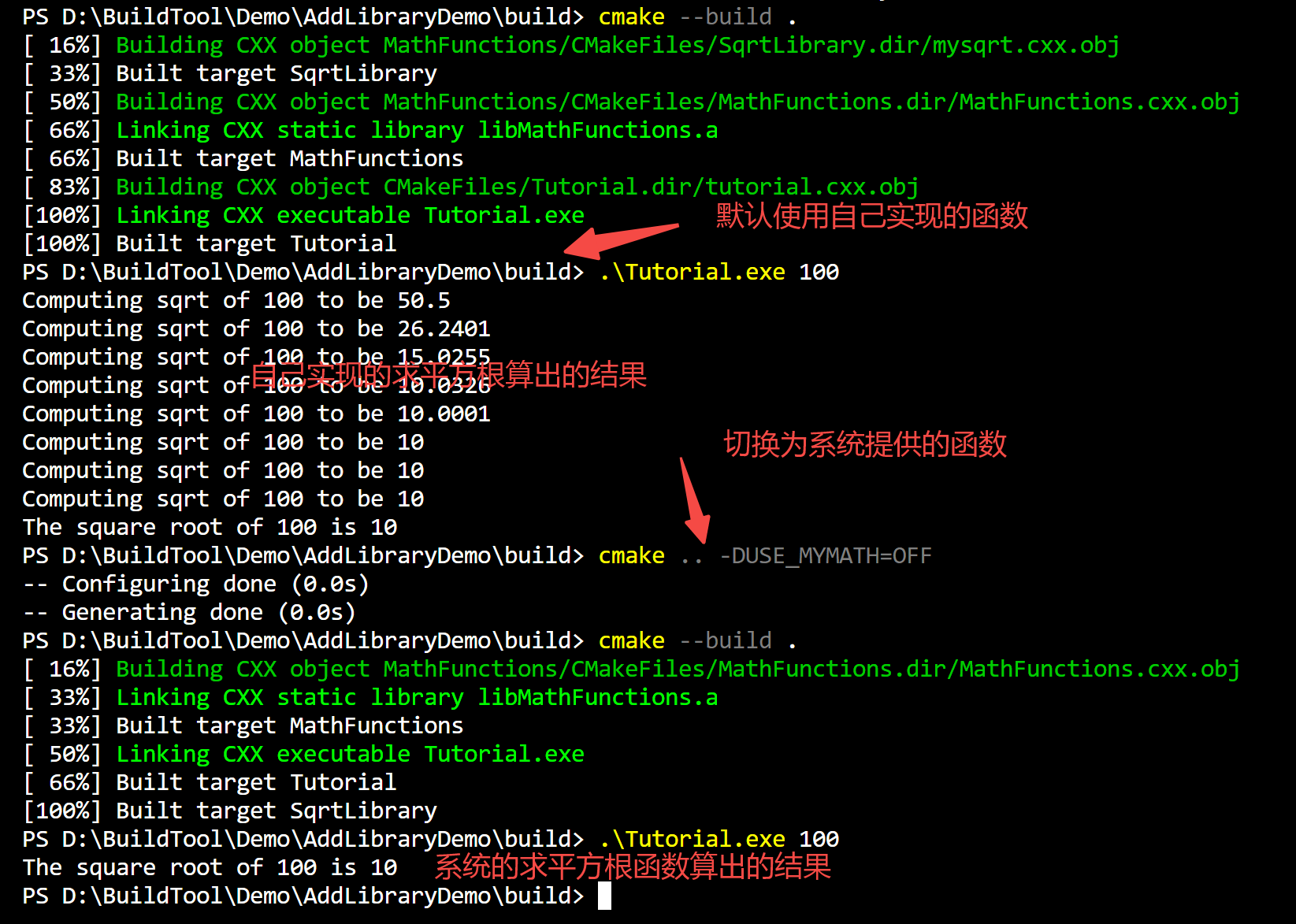
C/C++跨平台构建工具CMake-----灵活添加库并实现开发和生产环境的分离
目录 1.概述2.创建项目3 配置运行项目3.1 编写开平方根示例代码3.2 编写CMake构建脚本 4.使用子模块实现求平方根的功能4.1 在子模块中实现两种求平方根的方法4.2 构建Mathfunctions子模块4.3 在根目录引用子模块的功能4.3.1 编写构建脚本4.3.2 编写C代码使用MathFunctions库中…...

javascript判断对象中是否存在某个字段
1. in 如果指定的属性在指定的对象或其原型链中,则 in 运算符返回 true。 const car { make: Honda, model: Accord, year: 1998 };console.log(make in car); // truedelete car.make; if (make in car false) {car.make Suzuki; }console.log(car.make); //…...

网络基础-2
IEEE制定了一个名为GARP的协议框架,该框架协议包含了两个具体协议,GMRP和GVRP。GVRP可以大大降低VLAN配置过程中的手工的工作量。 IP本身是一个协议文件的名称,该协议主要定义阐释了IP报文的格式。 类型网络号位数网络号个数主机号位数每个…...

【MySQL索引与优化篇】索引的分类与设计原则
索引的分类与设计原则 文章目录 索引的分类与设计原则1. 索引的分类2. MySQL8.0索引新特性2.1 支持降序索引2.2 隐藏索引 3. 索引的设计原则3.1 适合索引的10个设计原则3.2 限制索引的数目3.3 不适合使用索引的情况 1. 索引的分类 从 功能逻辑 上说,索引主要有 4 种…...
基于Java的民航售票管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...
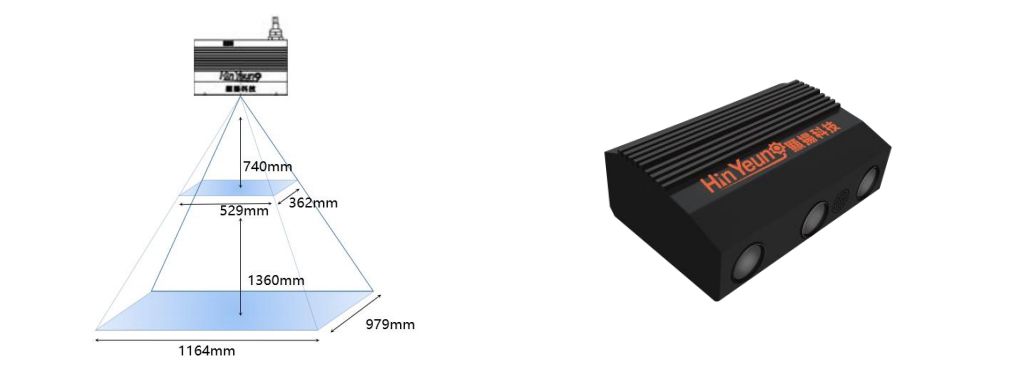
应用案例|基于三维机器视觉的机器人引导电动汽车充电头自动插拔应用方案
Part.1 项目背景 人类对减少温室气体排放、提高能源效率以及减少对化石燃料的依赖,加速了电动汽车的普及,然而,电动汽车的充电依然面临一些挑战。传统的电动汽车充电通常需要人工干预,插入和拔出充电头,这不仅可能导致…...
基于Java的流浪动物救助管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...

关于错误javax.net.ssl.SSLException: Received close_notify during handshake
今天开发的小伙伴遇到一问题,报错内容是: javax.net.ssl.SSLException: Received close_notify during handshake at sun.security.ssl.Alerts.getSSLException(Unknown Source) at sun.security.ssl.SSLSocketImpl.fatal(Unknown Source) at sun.securi…...

JAVA实现校园失物招领管理系统 开源
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 招领管理模块2.2 寻物管理模块2.3 系统公告模块2.4 感谢留言模块 三、界面展示3.1 登录注册3.2 招领模块3.3 寻物模块3.4 公告模块3.5 感谢留言模块3.6 系统基础模块 四、免责说明 一、摘要 1.1 项目介绍 基于VueSpri…...
基于Java的体育竞赛成绩管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...
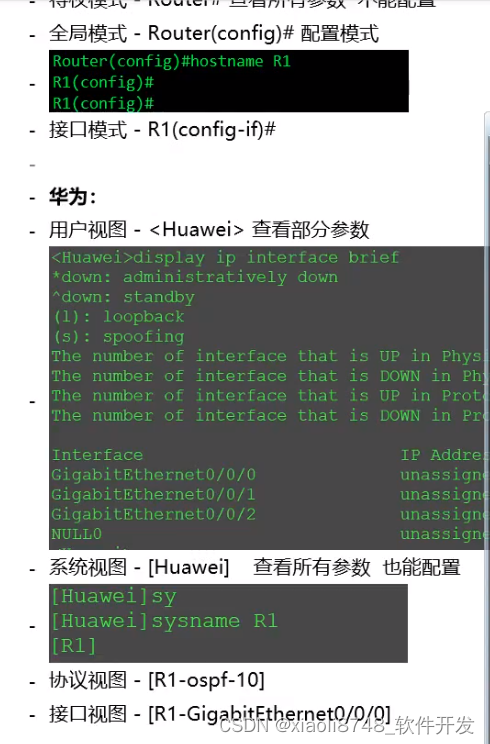
网络设备远程登录和管理-双厂商
✍ 设备开局都要做哪些配置? ✍ 思科华为的配置命令有什么区别? ✍ 实战演示不同操作系统的配置; -- 本地设备调试 - console接口配置 -- 远程设备管理 - telnet 不加密 | ssh 加密的 -- web界面调试 - 补充的作用 -- SD…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
