回溯法(1)--装载问题和0-1背包
一、回溯法
回溯法采用DFS+剪枝的方式,通过剪枝删掉不满足条件的树,提高本身作为穷举搜索的效率。
回溯法一般有子集树和排列树两种方式,下面的装载问题和01背包问题属于子集树的范畴。
解空间类型:
子集树:所给的问题是从n个元素的集合S中找出满足某种性质的子集,例如装载问题、0-1背包问题。
排列树:所给的问题是确定n个元素满足某种性质的排列,例如旅行商问题。
回溯法所搜索的解结果,都在树的叶子结点上,一般左树为添加元素(1),右树为不添加元素(0)。
剪枝策略:
左剪枝:当前扩展节点,加入左枝后,不符合约束条件要求,那么就直接剪掉这个子节点及其所有子树,不再继续搜索。
右剪枝:当前扩展节点,加入右枝后,已经无法继续寻求最优解,后续子树也无法存在最优解,或者相比于之前遍历的叶子结点来说,更好的最优解,那么就剪掉这个子节点及其所有子树,不再继续搜索。
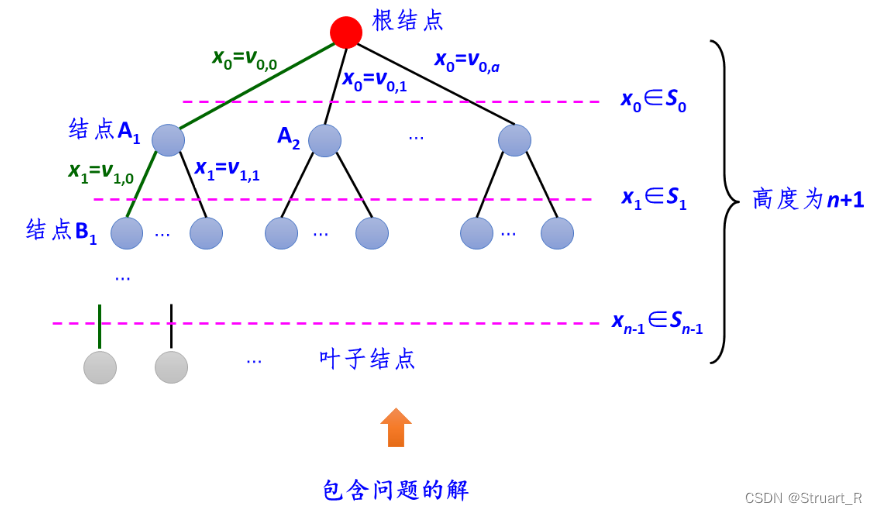
二、简单装载问题
1、算法设计
简单装载问题:n个集装箱装进一艘载重量为W的轮船,其中集装箱的重量为
,不考虑集装箱体积。设计一个算法,要求选择若干集装箱装进轮船,使得不超过载重量W,且给出可行解,和最优解的箱子装载方式。
算法:回溯法,子集树算法。
算法参数表:
num:选择的集装箱数
tw:选择的集装箱重量和
rw:剩余的集装箱重量和
op:表示是否选择该集装箱,op=1则选择,op=0则不选
x[ ]:最优解的op操作符选择,可以用来输出最优的集装箱装载方案
静态变量:
n:物品个数
w[ ]:各种物品的重量
W:轮船总重量限额
minnum:最优解集装箱存放个数
maxw:最优解的总重量
dfs策略:
(1)先判断是否为叶子结点,若是则判断该解是否为最优解,若是最优解则把op数组存入x数组。最优解条件:当前解集装箱存放个数是否小于最优解集装箱存放个数,且选择的集装箱和小于轮船限额
(2)若不是叶子结点则进行扩展操作。
(3)先进行左扩展,若tw+w[i]<=W,即加入这个物品后,总重量不大于轮船限额,则继续扩展,否则剪枝。
(4)再进行右扩展,若tw+rw-w[i]>=W,即不加入这个物品时,所选集装箱总重和未选集装箱总重的和仍然不小于轮船限额,则继续扩展,否则剪枝。
2、代码
//回溯法最优装载问题
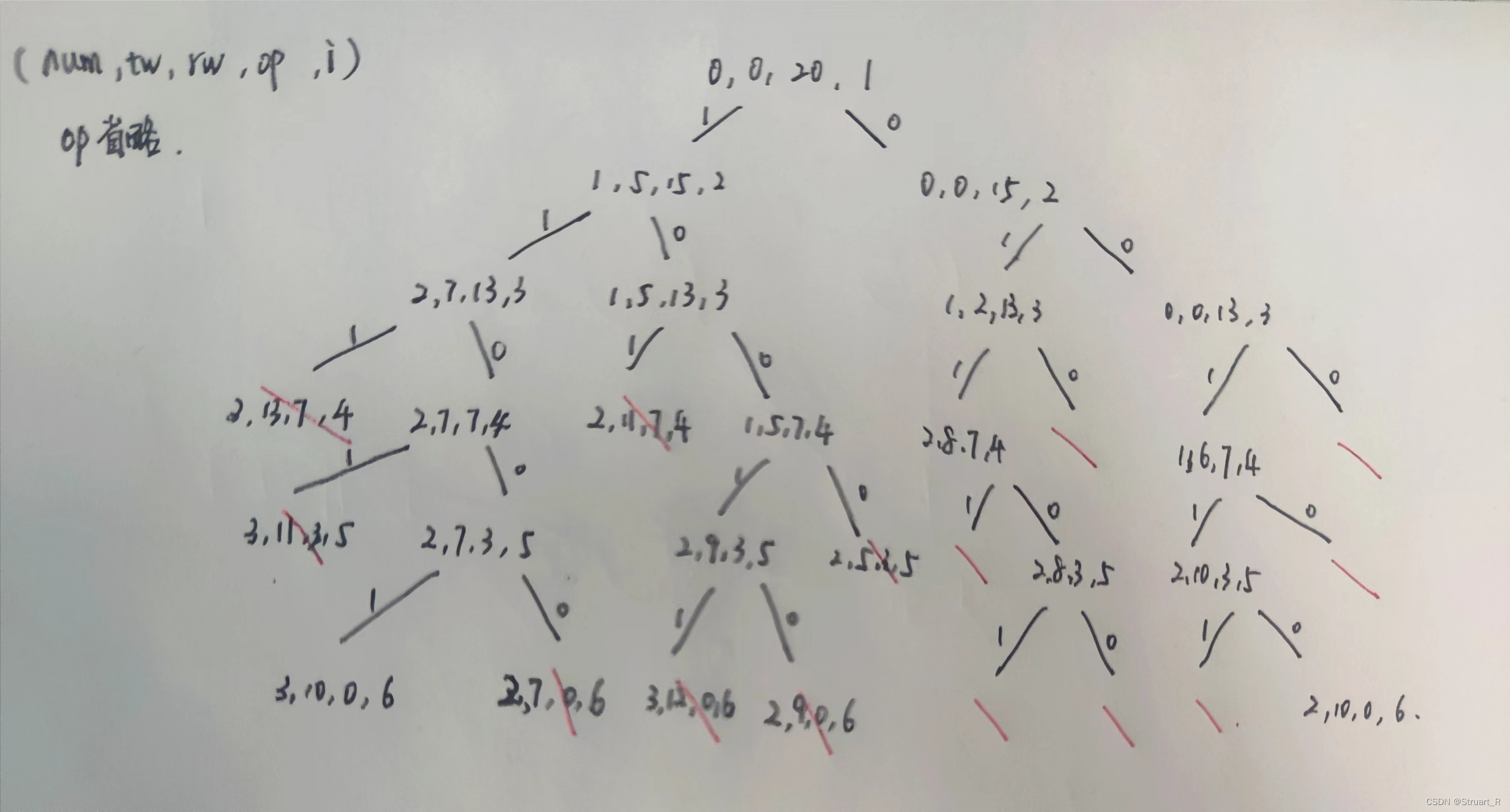
public class bestload {static int n=5;static int minnum=9999;static int W=10; //w为每个箱子重量static int maxw=0; //存放最优解总重量static int w[]={0,5,2,6,4,3};public static void main(String []args){int rw=0; //rw为剩余集装箱重量和for(int num:w)rw+=num;int op[]=new int[w.length]; //存放一个箱子是否装载int x[]=new int[w.length];System.out.println("所有可行解:");dfs(0,0,rw,op,1,x);System.out.println("最少物品的解:");for(int i=1;i<w.length;i++)if(x[i]==1)System.out.print(w[i]+" ");}public static void dfs(int num,int tw,int rw,int op[],int i,int x[]){if(i>n){if(tw<=W&&num<minnum){maxw=tw;minnum=num;for(int j=1;j<=n;j++) x[j]=op[j];}for(int j=1;j<=n;j++) if(op[j]==1)System.out.print(w[j]+" ");System.out.println(" ");}else{op[i]=1; //优先左分枝if(tw+w[i]<=W) //左分枝条件dfs(num+1,tw+w[i],rw-w[i],op,i+1,x);op[i]=0;if(tw+rw-w[i]>=W)dfs(num,tw,rw-w[i],op,i+1,x);}}
}子集树如下:(右树部分省略)
三、复杂装载问题
1、算法设计
复杂装载问题:n个集装箱要装进两艘载重量分别为c1和c2的轮船,其中集装箱的重量为
,不考虑集装箱体积,设计一个算法,使得这些集装箱装上这两艘轮船,如果不能装载则返回load false。
算法:回溯法,子集树算法,优先第一个轮船装载,判断第二个轮船是否能够装载剩余集装箱。
dfs策略:
(1)先判断是否为叶子结点,若是则判断该解是否为最优解,若是最优解则把op数组存入x数组。最优解条件:当前选择的集装箱和是否大于第一个轮船的最优集装箱装载重量,且选择的集装箱和小于第一个轮船限额
(2)若不是叶子结点则进行扩展操作。
(3)先进行左扩展,若tw+w[i]<=c1,即加入这个物品后,总重量不大于第一个轮船限额,则继续扩展,否则剪枝。
(4)再进行右扩展,若tw+rw-w[i]>=maxw,即不加入这个物品时,所选集装箱总重和未选集装箱总重的和仍然不小于第一个轮船的最优装载重量和,则继续扩展,否则剪枝。
2、代码
//回溯法复杂装载问题
public class complexbestload {static int n=3;static int minnum=9999;static int c1=50; //w为每个箱子重量static int c2=50;static int maxw=0; //存放最优解总重量static int w[]={0,10,40,40};public static void main(String []args){int rw=0; //rw为剩余集装箱重量和for(int num:w)rw+=num;int op[]=new int[w.length]; //存放一个箱子是否装载int x[]=new int[w.length];dfs(0,0,rw,op,1,x);judge(x);}public static void dfs(int num,int tw,int rw,int op[],int i,int x[]){if(i>n) //dfs搜索到最后一层,所有的货物都试了一遍,则输出最优解{if(tw<=c1&&tw>maxw){maxw=tw;for(int j=1;j<=n;j++)x[j]=op[j];}}else{op[i]=1; //优先左分枝if(tw+w[i]<=c1) //左分枝条件dfs(num+1,tw+w[i],rw-w[i],op,i+1,x);op[i]=0;if(tw+rw-w[i]>=maxw)dfs(num,tw,rw-w[i],op,i+1,x);}}public static void judge(int x[]){int total=0;for(int i=1;i<w.length;i++)if(x[i]==0)total+=w[i];if(total<=c2){System.out.print("c1:");for(int i=1;i<w.length;i++)if(x[i]==1)System.out.print(w[i]+" ");System.out.println();System.out.print("c2:");for(int i=1;i<w.length;i++)if(x[i]==0)System.out.print(w[i]+" ");} else System.out.println("load false");}
}
四、0-1背包问题
1、算法设计
0-1背包问题:给定n个物品和一个背包,物品重量为,价值为
,背包容量为c,请设计一种算法,放入若干物品后,背包中物品总价值最大。
算法:回溯法,子集树算法。左剪枝结合贪心算法。
初始化:首先对w数组和v数组进行重新排序,按照a数组,即单位重量价值最高的优先。下面代码使用快速排序。
dfs策略:
(1)先判断是否为叶子结点,若是则判断该解是否为最优解,若是最优解则把op数组存入x数组,最优解maxv替换为当前所选物品的总重量。最优解条件:当前所选物品总重量不大于背包限额,且所选物品的价值大于当前最优解maxv。
(2)若不是叶子结点则进行扩展操作。
(3)先进行左扩展,计算左分枝后,使用贪心算法计算已选物品与若干剩余物品,在背包未超重情况下的最大价值。若greed>maxv该最大价值已经大于当前已知最优解maxv且tw+w[i]<=W当前已选物品的总重量加上新物品仍然不大于背包限额,则进行扩展,否则剪枝。
(4)再进行右扩展,若tw+rw-w[i]>=maxw,即不加入这个物品时,所选物品总重和剩余物品总重的和仍然不小于背包限额,则继续扩展,否则剪枝。
2、代码
//回溯法解决0-1背包问题
public class backage {static int W=10;static int maxv=0; //存放最优解价值public static void main(String[] args){double w[]={0,2,1,3,4,6};double v[]={0,3,2,4,5,8};int n=w.length-1;double rw=0;double a[]=new double[w.length];int op[]=new int[w.length]; //存放当前叶子结点的解int x[]=new int[w.length]; //存放最优解for(int i=1;i<w.length;i++)a[i]=v[i]/w[i];for(int i=1;i<w.length;i++)rw+=w[i];//快排quickSort(a, w, v, 1, n);//回溯dfs(w,v,0,0,rw,op,x,1);int total=0;for(int j=1;j<w.length;j++){if(x[j]==1){ System.out.print(w[j]+" ");total+=v[j];}}System.out.println();System.out.println("Max value:"+total);}//快速排序public static void quickSort(double arr[],double w[],double v[],int low,int high){int i=low;int j=high;int t;if(low>high)return;double tmp=arr[low];while(i<j){while(i<j&&tmp>=arr[j]){j--;}; //注意由于降序排列,所以为tmp>=arr[j]while(i<j&&tmp<=arr[i]){i++;}; //同理,tmp<=arr[i]if(i<j){swap(arr,i,j);swap(w, i, j);swap(v,i,j);}}swap(arr,low,i);swap(w,low,i);swap(v,low,i);quickSort(arr, w,v,low, j-1);quickSort(arr,w,v,j+1,high);}//交换同一数组的两个值public static void swap(double arr[],int i,int j){double t;t=arr[i];arr[i]=arr[j];arr[j]=t;}//回溯法public static void dfs(double w[],double v[],int num,double tw, double rw, int op[],int x[],int i){if(i>w.length-1){if(tw<=W){int tot=0;for(int j=1;j<w.length;j++){if(op[j]==1){tot+=v[j];}}if(tot>maxv){for(int j=1;j<w.length;j++)x[j]=op[j];maxv=tot;}}}else{op[i]=1; //优先左分枝double greed=greedy(op, v, w, i);if(tw+w[i]<=W&&greed>maxv) //左分枝条件dfs(w,v,num+1,tw+w[i],rw-w[i],op,x,i+1);op[i]=0;if(tw+rw-w[i]>=W)dfs(w,v,num,tw,rw-w[i],op,x,i+1);}}//左剪枝贪心计算public static double greedy(int op[],double v[],double w[],int i){double totv=0;double totw=0;for(int j=1;j<=i;j++){if(op[j]==1){ totv+=v[j];totw+=w[j];}}for(int j=i+1;j<w.length;j++){if(totw+w[j]<W){totw+=w[j];totv+=v[j];}else{totv+=(W-totw)*v[j]/w[j];totw=W;break;}}return totv;}
}相关文章:
回溯法(1)--装载问题和0-1背包
一、回溯法 回溯法采用DFS+剪枝的方式,通过剪枝删掉不满足条件的树,提高本身作为穷举搜索的效率。 回溯法一般有子集树和排列树两种方式,下面的装载问题和01背包问题属于子集树的范畴。 解空间类型: 子集树࿱…...
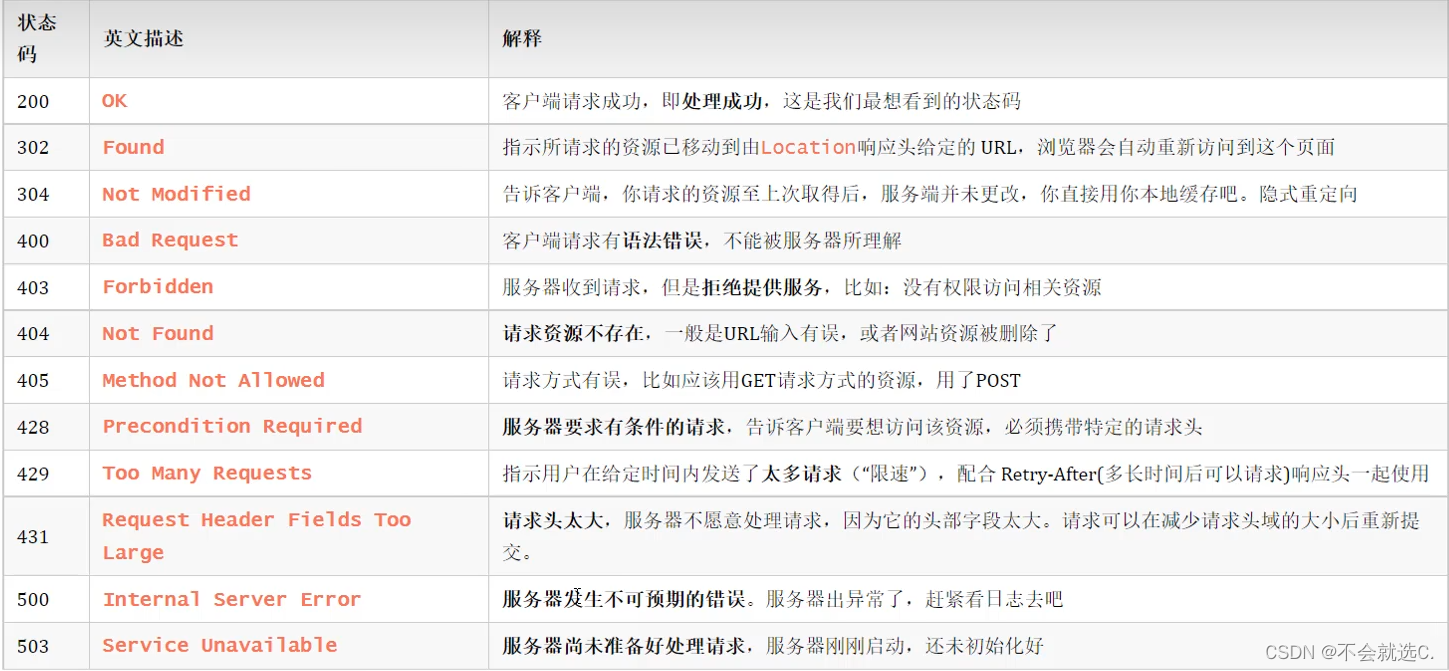
[javaweb]——HTTP请求与响应协议,常见响应状态码(如:404)
🌈键盘敲烂,年薪30万🌈 目录 HTTP概述 📕概念:Hyper Text Transfer Protocol,超文本传输协议,规定了浏览器和服务器之间数据传输的规则。 📕特点: 📕插播…...

Java面向对象(进阶)-- 拼电商客户管理系统(康师傅)
文章目录 一、目标二、需求说明(1)主菜单(2)添加客户(3)修改客户(4)删除客户(5)客户列表 三、软件设计结构四、类的设计(1)Customer类…...

Qt配置OpenCV教程,亲测已试过
详细版可参考:Qt配置OpenCV教程,亲测已试过(详细版)_qt opencv_-_Matrix_-的博客-CSDN博客 软件准备:QtOpenCVCMake (QtOpenCV安装不说了,CMake的安装,我用的是:可参考博客&#x…...

【实用网站分享】
1、PyDebloatX https://pydebloatx.com/pydebloatx 是一种用于 Windows 操作系统的 Python 脚本,用于卸载 Windows 10 系统中的预装应用和系统组件,以便提高系统性能和释放磁盘空间。它是 Debloat Windows 10 脚本的一个分支,但具有更友好和…...
问题 U: 折线分割平面(类比+规律)
规律类比: 1.一个折线的角,只会对应一个部分 2.若反向延长,角对应的部分被分为3部分 (即一条折现线改为两条直线) 3.所以n条折线分成的平面数,等于2n条直线减去2n 代码实现:...

npm 彻底卸载
问题: 执行 npm -v 指令出现如下报错: ERROR: npm v10.2.1 is known not to run on Node.js v12.10.0. This version of npm supports the following node versions: ^18.17.0 || >20.5.0. 分析: 由于编译环境问题,需要更新…...
云安全-云原生技术架构(Docker逃逸技术-特权与危险挂载)
0x00 云原生技术-docker docker容器和虚拟机的对比:前者是将运行环境打包,封装一个环境。后者是将整个系统打包,封装一个系统。在操作使用上来说各有利弊。 0x01 docker容器的三种逃逸类型 特权模式启动(不安全的启动方式&…...
【Python爬虫三天从0到1】Day1:爬虫核心
目录 1.HTTP协议与WEB开发 (1)简介 (2)请求协议和响应协议 2. requests&反爬破解 (1)UA反爬 (2)referer反爬 (3)cookie反爬 3.请求参数 &#x…...

2023-10 最新jsonwebtoken-jjwt 0.12.3 基本使用
导入依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.12.3</version></dependency>包括了下面三个依赖, 所以导入上面一个就OK了 <dependency><groupId>io.jsonwe…...

云起无垠典型案例入选《2023软件供应链安全洞察》报告
近日,历时6个月,由ISC编制的《2023软件供应链安全洞察》报告(以下简称《报告》)正式对外发布。《报告》围绕软件供应链安全现状、技术内核、治理指南、落地实践展开,以期为行业从业者提供有价值的信息和洞见࿰…...
)
怎么从休学证明中取出休学原因(python自动化办公,涉及word和excel)
怎么从休学证明中取出休学原因(python自动化办公,涉及word和excel) 本代码偏向处理高校教务处的工作 休学或请假模板如下: 休学证明(此联存教务办)编号:休202323 计算机系23级计算机科学与技术…...
C语言 定义一个函数,并调用,该函数中打印显示直角三角形
#include<stdio.h> void chengfabiao() {for (int i 1; i < 5; i){for (int j 1; j < i; j){printf("*");} printf("\n");} } int main(int argc,const char *argv[]) {chengfabiao();return 0; }...

Doceker-compose——容器群集编排管理工具
目录 Docker-compose 1、Docker-compose 的三大概念 2、YAML文件格式及编写注意事项 1)使用 YAML 时需要注意下面事项 2)ymal文件格式 3)json格式 3、Docker Compose配置常用字段 4、Docker-compose的四种重启策略 5、Docker Compos…...

Redis 与 MySQL 一致性 实现方案
正常情况下的流程是:请求来了,先检查 Redis 有没有数据,有返回;没有便查询 MySQL 然后 放入 Redis。 此时,如果 MySQL 的数据发生了变化,所以需要同步到 Redis 中。 解决方法:MySQL 中的数据更新…...

运维 | 使用 Docker 安装 Jenkins | Jenkins
运维 | 使用 Docker 安装 Jenkins | Jenkins 前言 本期内容主要是为了学习如何通过 Docker 安装Jenkins,仅作为记录与参考,希望对大家有所帮助。 准备工作 系统:CentOS 7.9配置:4c8g 快速安装 下面以 Docker 方式安装 Jenkin…...
linux-磁盘应用
目录 一、磁盘内容简述 1、一些基本概念 2、分区简述 3、常见文件系统 4、linux硬盘文件 二、对linux系统进行分区 1、用fdisk进行分区 2、用parted进行分区 一、磁盘内容简述 1、一些基本概念 - 扇区大小:512Btyes,0.5KB - 磁盘最小存储单位&…...
java版直播商城平台规划及常见的营销模式 电商源码/小程序/三级分销+商城免费搭建
涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis …...

软考高级之系统架构师之软件工程
软件工程 面向对象设计原则 单一职责:设计目的单一的类开闭原则;对扩展开放,对修改关闭里氏替换:子类可以替代父类依赖倒置:要依赖于抽象,而不是实现。要针对接口编程,不要针对实现编程接口隔…...
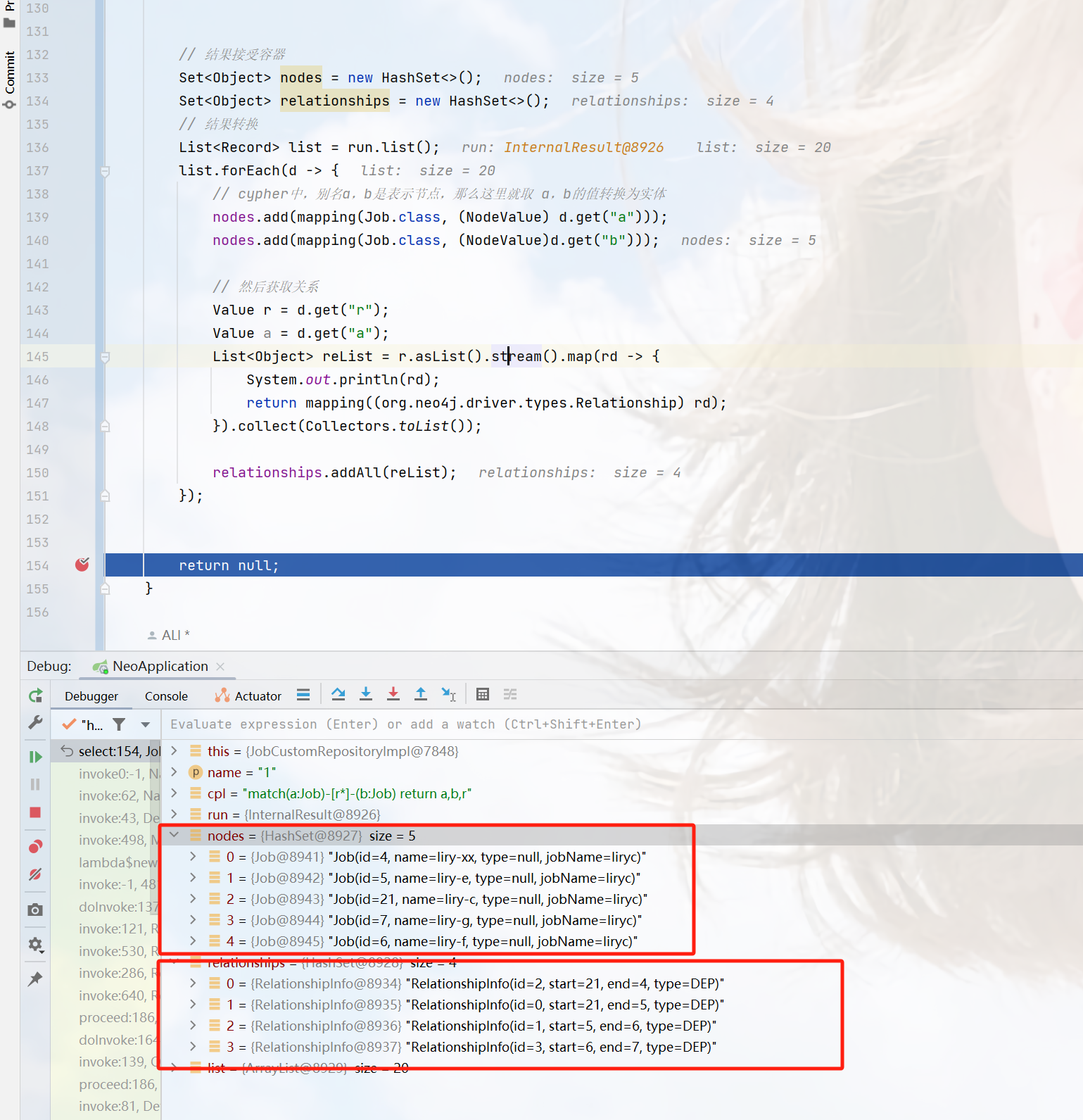
SpringBoot集成与应用Neo4j
文章目录 前言集成使用定义实体配置定义Repository查询方法方式一:Query方式二:Cypher语法构建器方式三:Example条件构建器方式四:DSL语法 自定义方法自定义接口继承自定义接口实现自定义接口neo4jTemplateNeo4jClient 自定义抽象…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...
