2023辽宁省赛E
Solution
题目大致分为三个步骤
- 计算 P ( S ) P(S) P(S)
- 证明删除区间连续且找到最值位置
- 根据最值位置求出答案
接下来过程中不合法的组合数都默认为 0 0 0
第 1 步 - 求出总值
考虑 S m = { 1 , 2 , ⋯ , m } S_m = \{1, 2, \cdots, m\} Sm={1,2,⋯,m} , 则有 $P(S_{n+2}) = P(S_{n+1})+P(S_{n}) $
因为
P ( S n ) = ∑ i = 1 n ( n − i i − 1 ) , P ( S n + 1 ) = ∑ i = 1 n + 1 ( n + 1 − i i − 1 ) , P ( S n + 2 ) = ∑ i = 1 n + 2 ( n + 2 − i i − 1 ) P(S_n) = \sum_{i=1}^n \binom{n-i}{i-1} \ , \ P(S_{n+1}) = \sum_{i=1}^{n+1} \binom{n+1-i}{i-1} \ , \ P(S_{n+2}) = \sum_{i=1}^{n+2} \binom{n+2-i}{i-1} P(Sn)=i=1∑n(i−1n−i) , P(Sn+1)=i=1∑n+1(i−1n+1−i) , P(Sn+2)=i=1∑n+2(i−1n+2−i)
利用公式
( n m ) = ( n − 1 m ) + ( n − 1 m − 1 ) \binom{n}{m} = \binom{n-1}{m} + \binom{n-1}{m-1} (mn)=(mn−1)+(m−1n−1)
可以得到
P ( S n + 2 ) = ∑ i = 1 n + 2 ( n + 2 − i i − 1 ) = ∑ i = 2 n + 1 ( n + 1 − i i − 1 ) + ∑ i = 2 n + 1 ( n + 1 − i i − 2 ) + ( n + 2 − 1 0 ) + ( n + 2 − ( n + 2 ) n + 2 ) = ∑ i = 1 n + 1 ( n + 1 − i i − 1 ) − 1 + ∑ i = 1 n ( n − i i − 1 ) + 1 = P ( S n + 1 ) + P ( S n ) \begin{aligned} P(S_{n+2}) &= \sum_{i=1}^{n+2} \binom{n+2-i}{i-1} \\ &= \sum_{i=2}^{n+1} \binom{n+1-i}{i-1} + \sum_{i=2}^{n+1} \binom{n+1-i}{i-2} + \binom{n+2-1}{0} + \binom{n+2-(n+2)}{n+2} \\ &= \sum_{i=1}^{n+1} \binom{n+1-i}{i-1}-1 +\sum_{i=1}^{n}\binom{n-i}{i-1} + 1 \\ &= P(S_{n+1}) + P(S_n) \end{aligned} P(Sn+2)=i=1∑n+2(i−1n+2−i)=i=2∑n+1(i−1n+1−i)+i=2∑n+1(i−2n+1−i)+(0n+2−1)+(n+2n+2−(n+2))=i=1∑n+1(i−1n+1−i)−1+i=1∑n(i−1n−i)+1=P(Sn+1)+P(Sn)
其中 P ( S 1 ) = 1 P(S_1) = 1 P(S1)=1 , P ( S 2 ) = 1 P(S_2) = 1 P(S2)=1 , 所以 P ( S n ) = f i b ( n ) P(S_n) = \mathrm{fib}(n) P(Sn)=fib(n)
或者由恒等式
∑ i = 0 ⌊ n / 2 ⌋ ( n − i i ) = f i b ( n + 1 ) \sum_{i=0}^{\lfloor n/2 \rfloor} \binom{n-i}{i} = \mathrm{fib}(n+1) i=0∑⌊n/2⌋(in−i)=fib(n+1)
然后
P ( S n ) = ∑ i = 1 n ( n − i i − 1 ) = ∑ i = 0 n − 1 ( ( n − 1 ) − i i ) = f i b ( n ) \begin{aligned} P(S_n) &= \sum_{i=1}^n \binom{n-i}{i-1} \\ &= \sum_{i=0}^{n-1} \binom{(n-1)-i}{i} \\ &= \mathrm{fib}(n) \end{aligned} P(Sn)=i=1∑n(i−1n−i)=i=0∑n−1(i(n−1)−i)=fib(n)
第 2 步 - 证明连续
最为关键的一点是 , 删点顺序不影响答案(我们将所有数当成数轴的点以简化说明) , 所以我们记 F ( x 1 , ⋯ , x r , x ) F(x_1,\cdots,x_r, x) F(x1,⋯,xr,x) 为去掉点 x 1 , ⋯ , x r x_1,\cdots,x_r x1,⋯,xr 后再删掉点 x x x 少的贡献 , 这里我们钦定 x 1 > x 2 > ⋯ > x r > x x_1 > x_2 > \cdots > x_r > x x1>x2>⋯>xr>x
首先考虑仅删除一个点时少掉的贡献 , 假设删除的位置是 x x x , 有
F ( x ) = ( n − x x − 1 ) + ∑ i = 1 x − 1 ( n − i − 1 i − 2 ) F(x) = \binom{n-x}{x-1} + \sum_{i=1}^{x-1} \binom{n-i-1}{i-2} F(x)=(x−1n−x)+i=1∑x−1(i−2n−i−1)
我们尝试找一找 F ( x ) F(x) F(x) 的最值点(如果只删掉一个点肯定是越大越好) , 有
F ( x + 1 ) − F ( x ) = ( n − x − 1 x ) − ( n − x x − 1 ) + ( n − x − 1 x − 2 ) = ( n − x − 1 x ) − ( n − x − 1 x − 1 ) − ( n − x − 1 x − 2 ) + ( n − x − 1 x − 2 ) = ( n − x − 1 x ) − ( n − x − 1 x − 1 ) \begin{aligned} F(x+1) - F(x) &= \binom{n-x-1}{x} - \binom{n-x}{x-1} + \binom{n-x-1}{x-2} \\ &= \binom{n-x-1}{x} - \binom{n-x-1}{x-1} - \binom{n-x-1}{x-2} + \binom{n-x-1}{x-2} \\ &= \binom{n-x-1}{x} - \binom{n-x-1}{x-1} \end{aligned} F(x+1)−F(x)=(xn−x−1)−(x−1n−x)+(x−2n−x−1)=(xn−x−1)−(x−1n−x−1)−(x−2n−x−1)+(x−2n−x−1)=(xn−x−1)−(x−1n−x−1)
可以发现 F ( x ) F(x) F(x) 是先增后减的单峰函数(最值点唯一或相邻两个) , 且最值点位置关系有
⌈ n − x ′ − 1 2 ⌉ = x ′ o r ⌊ n − x ′ − 1 2 ⌋ = x ′ \lceil \cfrac{n-x'-1}{2} \rceil = x' \ or \ \lfloor \cfrac{n-x'-1}{2} \rfloor = x' ⌈2n−x′−1⌉=x′ or ⌊2n−x′−1⌋=x′
现在我们考虑删除两个点时的情况 , 我们来考虑 F ( x 1 , x ) F(x_1,x) F(x1,x) 的最值点(不一定能取到) , 有
F ( x 1 , x ) = ( ( n − 1 ) − x x − 1 ) + ∑ i = 1 x − 1 ( ( n − 1 ) − i − 1 i − 2 ) F(x_1,x) = \binom{(n-1)-x}{x-1} + \sum_{i=1}^{x-1} \binom{(n-1)-i-1}{i-2} F(x1,x)=(x−1(n−1)−x)+i=1∑x−1(i−2(n−1)−i−1)
(因为删除 x 1 x_1 x1 对删除 x x x 的影响一定是"比 i i i ( 1 ≤ i ≤ x 1 − 1 1 \leq i \leq x_1-1 1≤i≤x1−1) 大的数少了一个")
有一种更感性的理解方法 , 因为 x < x 1 x < x_1 x<x1 所以我们可以将 x 1 + 1 x_1+1 x1+1 到 n n n 重标号为 x 1 x_1 x1 到 n − 1 n-1 n−1 , 问题就转化为了从 1 1 1 到 n − 1 n-1 n−1 的子问题
类比之前的求法可以得到 F ( x 1 , x ) F(x_1,x) F(x1,x) 的最值点位置关系有
⌈ ( n − 1 ) − x ′ − 1 2 ⌉ = x ′ o r ⌊ ( n − 1 ) − x ′ − 1 2 ⌋ = x ′ \lceil \cfrac{(n-1)-x'-1}{2} \rceil = x' \ or \ \lfloor \cfrac{(n-1)-x'-1}{2} \rfloor = x' ⌈2(n−1)−x′−1⌉=x′ or ⌊2(n−1)−x′−1⌋=x′
依此类推 , 可以证明 F ( x 1 , ⋯ , x k − 1 , x ) F(x_1, \cdots, x_{k-1}, x) F(x1,⋯,xk−1,x) 的最值点位置关系有
⌈ ( n − k ) − x k ′ 2 ⌉ = x k ′ o r ⌊ ( n − k ) − x k ′ 2 ⌋ = x k ′ \lceil \cfrac{(n-k)-x'_k}{2} \rceil = x'_k \ or \ \lfloor \cfrac{(n-k)-x'_k}{2} \rfloor = x'_k ⌈2(n−k)−xk′⌉=xk′ or ⌊2(n−k)−xk′⌋=xk′
去掉取整符号可以得到
( n − k ) − 1 ≤ 3 x k ′ ≤ ( n − k ) + 1 (n-k)-1 \leq 3x'_k \leq (n-k)+1 (n−k)−1≤3xk′≤(n−k)+1
这说明 − 1 ≤ x k + 1 ′ − x k ′ ≤ 0 -1 \leq x_{k+1}'- x_k' \leq 0 −1≤xk+1′−xk′≤0
接下来我们要证明删除序列为连续的一段
假定目前已经删除了 r r r 个点 , 且删的第 r r r 个点满足 x r ≤ x r ′ x_r \leq x_r' xr≤xr′ , 由上面不等式有 x r + 1 ′ = x r ′ x'_{r+1} = x'_r xr+1′=xr′ 或者 x r + 1 ′ = x r ′ − 1 x'_{r+1}=x'_r-1 xr+1′=xr′−1
由前论 F F F 的性质 , 可知 x r + 1 = x r − 1 x_{r+1} = x_r-1 xr+1=xr−1 时 F ( x 1 , ⋯ , x r + 1 ) F(x_1,\cdots,x_{r+1}) F(x1,⋯,xr+1) 最大 , 归纳可得 x r , ⋯ , x m x_r,\cdots, x_m xr,⋯,xm 连续
我们不妨假设第 k k k 次删除的点是第一个满足 x k = x k ′ x_k = x'_k xk=xk′ 的 , 即它是第一个删除点等于对应最值点的
有 x k ′ < x k − 1 < ⋯ < x 1 x'_k < x_{k-1} < \cdots < x_1 xk′<xk−1<⋯<x1 , 考虑 F ( x ) , F ( x 1 , x ) , ⋯ , F ( x 1 , ⋯ , x k − 2 , x ) F(x), F(x_1,x) ,\cdots , F(x_1,\cdots,x_{k-2},x) F(x),F(x1,x),⋯,F(x1,⋯,xk−2,x)
可以发现在 x k ′ < x k − 1 x'_k<x_{k-1} xk′<xk−1 的限制下根据最值点的不等式 , F ( x 1 , ⋯ , x k − 2 , x ) F(x_1,\cdots,x_{k-2},x) F(x1,⋯,xk−2,x) 可以取到的最大值点一定为 x k ′ + 1 x'_k+1 xk′+1
同理可得 x i = x k ′ + ( k − i ) x_i = x'_k + (k-i) xi=xk′+(k−i) , 这说明 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk 连续
如果不存在这样的 k k k , 那么可以分为两种情况
- 对于所有的 x i x_i xi , 要么 x i < x i ′ x_i < x'_i xi<xi′ 要么 x i > x i ′ x_i > x'_i xi>xi′
- 存在 k k k 使得 x k > x k ′ x_k > x'_k xk>xk′ 且 x k + 1 < x k + 1 ′ x_{k+1} < x'_{k+1} xk+1<xk+1′
对于情况 1 , 将 x m x_m xm 或 x 1 x_1 x1 移动到最值点处会更优
对于情况 2 , 将 x k + 1 x_{k+1} xk+1 移动到其最值点上会更优
这说明了最优解的删除方法至少有一次满足 x k = x k ′ x_k = x'_k xk=xk′ , 这样的 k k k 必定存在
综上 , 删除区间连续
这部分简单地说 , 就是如果将删除的数定序为从大到小 , 那么删一个点后减掉的贡献只和前面删数的数量相关(当然要考虑最值点的位置) , 而又由于最值点之间相距很近 , 所以删除序列连续
第三步 - 求出贡献
现在不妨假设我们删了 l l l 到 r r r , 现在我们来寻找使得答案最小的 l l l 和 r r r
我们从最后的答案 P ( S ′ ) P(S') P(S′) 来分析 , 则最小的 P ( S l , r ) P(S_{l,r}) P(Sl,r) ( S S S 删除 l l l 到 r r r 的数) 对应我们所要的 l l l 和 r r r
P ( S l , r ) = ∑ i = 1 l − 1 ( n − ( r − l + 1 ) − i i − 1 ) + ∑ i = r + 1 n ( n − i i − 1 ) P(S_{l,r}) = \sum_{i=1}^{l-1} \binom{n-(r-l+1)-i}{i-1} + \sum_{i=r+1}^n \binom{n-i}{i-1} P(Sl,r)=i=1∑l−1(i−1n−(r−l+1)−i)+i=r+1∑n(i−1n−i)
依旧做差
P ( S l + 1 , r + 1 ) − P ( S l , r ) = ∑ i = 1 l ( n − ( r − l + 1 ) − i i − 1 ) + ∑ i = r + 2 n ( n − i i − 1 ) − ∑ i = 1 l − 1 ( n − ( r − l + 1 ) − i i − 1 ) − ∑ i = r + 1 n ( n − i i − 1 ) = ( n − ( r − l + 1 ) − l l − 1 ) − ( n − r − 1 r ) = ( n − r − 1 l − 1 ) − ( n − r − 1 r ) \begin{aligned} P(S_{l+1,r+1}) -P(S_{l,r}) &= \sum_{i=1}^{l} \binom{n-(r-l+1)-i}{i-1} + \sum_{i=r+2}^n \binom{n-i}{i-1} - \sum_{i=1}^{l-1} \binom{n-(r-l+1)-i}{i-1} - \sum_{i=r+1}^n \binom{n-i}{i-1} \\ &= \binom{n-(r-l+1)-l}{l-1} - \binom{n-r-1}{r} \\ &= \binom{n-r-1}{l-1} - \binom{n-r-1}{r} \end{aligned} P(Sl+1,r+1)−P(Sl,r)=i=1∑l(i−1n−(r−l+1)−i)+i=r+2∑n(i−1n−i)−i=1∑l−1(i−1n−(r−l+1)−i)−i=r+1∑n(i−1n−i)=(l−1n−(r−l+1)−l)−(rn−r−1)=(l−1n−r−1)−(rn−r−1)
可以通过分析得到 P ( S l , r ) P(S_{l,r}) P(Sl,r) 是单峰函数且最小值点要么有一个 , 要么有相邻的两个 , 且有
r = n + m − 1 3 r = \frac{n+m-1}{3} r=3n+m−1
这样我们就确定了删除的范围 l l l , r r r ( r ≥ m r \geq m r≥m)
接下来我们来计算 P ( S l , r ) m o d p P(S_{l,r}) \ \mathrm{mod}\ p P(Sl,r) mod p , 观察式子 , 实际上我们要计算的是
f ( a , n ) = ∑ i = 0 a ( n − i i ) m o d p f(a,n) = \sum_{i=0}^{a} \binom{n-i}{i} \ \mathrm{mod} \ p f(a,n)=i=0∑a(in−i) mod p
若 n ≤ p n \leq p n≤p , 则上式可以在预处理后暴力计算 , 复杂度 Θ ( p ) \Theta(p) Θ(p) , 以下假定 n > p n > p n>p
根据 Lucas 定理稍作变换
f ( a , n ) = ∑ i = 0 a ( n − i i ) m o d p = ∑ i = 0 a ( ⌊ ( n − i ) / p ⌋ ⌊ i / p ⌋ ) ( ( n − i ) % p i % p ) m o d p = ∑ i = 0 p − 1 ( ( n − i ) % p i ) ∑ j = 0 ⌊ a / p ⌋ − 1 ( ⌊ ( n − i ) / p ⌋ − j j ) + ∑ i = 0 a % p ( ( n − i ) % p i ) ( ⌊ ( n − i ) / p ⌋ − ⌊ a / p ⌋ ⌊ a / p ⌋ ) m o d p = g ( a , n ) + h ( a , n ) \begin{aligned} f(a,n) &= \sum_{i=0}^{a} \binom{n-i}{i} \ \mathrm{mod} \ p \\ &= \sum_{i=0}^{a} \binom{\lfloor (n-i)/p \rfloor}{\lfloor i/p \rfloor} \binom{(n-i) \% p}{i \% p} \ \mathrm{mod} \ p \\ &= \sum_{i=0}^{p-1} \binom{(n-i) \% p}{i} \sum_{j=0}^{\lfloor a/p \rfloor-1} \binom{\lfloor (n-i)/p \rfloor-j}{j} + \sum_{i=0}^{a\%p} \binom{(n-i) \% p}{i}\binom{\lfloor (n-i)/p \rfloor-\lfloor a/p \rfloor}{\lfloor a/p \rfloor} \ \mathrm{mod} \ p \\ &= g(a,n)+ h(a,n) \end{aligned} f(a,n)=i=0∑a(in−i) mod p=i=0∑a(⌊i/p⌋⌊(n−i)/p⌋)(i%p(n−i)%p) mod p=i=0∑p−1(i(n−i)%p)j=0∑⌊a/p⌋−1(j⌊(n−i)/p⌋−j)+i=0∑a%p(i(n−i)%p)(⌊a/p⌋⌊(n−i)/p⌋−⌊a/p⌋) mod p=g(a,n)+h(a,n)
因为 ⌊ ( n − i ) / p ⌋ \lfloor (n-i)/p \rfloor ⌊(n−i)/p⌋ 只会在 i = n % p i=n\%p i=n%p 到 i = n % p + 1 i=n\%p+1 i=n%p+1 内变一次 , 所以我们可以将 g ( a , n ) g(a,n) g(a,n) 拆分
g ( a , n ) = ∑ i = 0 p − 1 ( ( n − i ) % p i ) ∑ j = 0 ⌊ a / p ⌋ − 1 ( ⌊ ( n − i ) / p ⌋ − j j ) m o d p = [ ∑ i = 0 n % p ( n % p − i i ) + ∑ i = n % p + 1 p − 1 ( n % p + p − i i ) ] ∑ j = 0 ⌊ a / p ⌋ − 1 ( ⌊ ( n − i ) / p ⌋ − j j ) m o d p = ∑ i = 0 n % p ( n % p − i i ) ∑ j = 0 ⌊ a / p ⌋ − 1 ( ⌊ n / p ⌋ − j j ) + ∑ i = n % p + 1 p − 1 ( n % p + p − i i ) ∑ j = 0 ⌊ a / p ⌋ − 1 ( ⌊ n / p ⌋ − 1 − j j ) m o d p = f ( n % p , n % p ) f ( ⌊ a / p ⌋ − 1 , ⌊ n / p ⌋ ) + [ f ( p − 1 , n % p + p ) − f ( n % p , n % p + p ) ] f ( ⌊ a / p ⌋ − 1 , ⌊ n / p ⌋ − 1 ) m o d p \begin{aligned} g(a,n) &= \sum_{i=0}^{p-1} \binom{(n-i) \% p}{i} \sum_{j=0}^{\lfloor a/p \rfloor-1} \binom{\lfloor (n-i)/p \rfloor-j}{j}\ \mathrm{mod} \ p \\ &= \left[ \sum_{i=0}^{n\%p}\binom{n\% p - i}{i} + \sum_{i=n\%p+1}^{p-1}\binom{n\% p + p - i}{i} \right] \sum_{j=0}^{\lfloor a/p \rfloor-1} \binom{\lfloor (n-i)/p \rfloor-j}{j}\ \mathrm{mod} \ p \\ &= \sum_{i=0}^{n\%p}\binom{n\% p - i}{i}\sum_{j=0}^{\lfloor a/p \rfloor-1} \binom{\lfloor n/p \rfloor-j}{j}\ + \sum_{i=n\%p+1}^{p-1}\binom{n\% p + p - i}{i} \sum_{j=0}^{\lfloor a/p \rfloor-1} \binom{\lfloor n/p \rfloor-1-j}{j}\ \mathrm{mod} \ p \\ &= f(n\%p, n\%p)f(\lfloor a/p \rfloor-1, \lfloor n/p \rfloor) +\\ &\ \ \ \ \left[ f(p-1,n\%p+p)-f(n\%p,n\%p+p) \right] f(\lfloor a/p \rfloor-1, \lfloor n/p \rfloor-1)\ \mathrm{mod} \ p \\ \end{aligned} g(a,n)=i=0∑p−1(i(n−i)%p)j=0∑⌊a/p⌋−1(j⌊(n−i)/p⌋−j) mod p= i=0∑n%p(in%p−i)+i=n%p+1∑p−1(in%p+p−i) j=0∑⌊a/p⌋−1(j⌊(n−i)/p⌋−j) mod p=i=0∑n%p(in%p−i)j=0∑⌊a/p⌋−1(j⌊n/p⌋−j) +i=n%p+1∑p−1(in%p+p−i)j=0∑⌊a/p⌋−1(j⌊n/p⌋−1−j) mod p=f(n%p,n%p)f(⌊a/p⌋−1,⌊n/p⌋)+ [f(p−1,n%p+p)−f(n%p,n%p+p)]f(⌊a/p⌋−1,⌊n/p⌋−1) mod p
令 T ( n ) T(n) T(n) 代表计算 f ( a , n ) f(a,n) f(a,n) 的复杂度上界 , 计算 h ( a , n ) h(a,n) h(a,n) 的复杂度为 p log n < 2 C p \log n < 2C plogn<2C , 则有
T ( n ) = 2 ∗ T ( n / p ) + 2 C T(n) = 2*T(n/p) + 2C T(n)=2∗T(n/p)+2C
其中 T ( 1 ) = 1 T(1)=1 T(1)=1 , 令 m = log p n m = \log_p n m=logpn 则有
T ′ ( m ) = 2 ∗ T ′ ( m − 1 ) + 2 C T'(m) = 2*T'(m-1) + 2C T′(m)=2∗T′(m−1)+2C
推得
T ′ ( m ) = 2 m × 2 C T'(m) = 2^m \times 2C T′(m)=2m×2C
所以
T ( n ) = 2 log p n × 2 C = n log p 2 × 2 C = n log p 2 × 2 p log n T(n) = 2^{\log_pn} \times 2C = n^{\log_p 2} \times 2C = n^{\log_p 2} \times 2p \log n T(n)=2logpn×2C=nlogp2×2C=nlogp2×2plogn
当 p > 2 p > 2 p>2 时复杂度满足要求
当 p = 2 p=2 p=2 时 , 发现 g ( a , n ) g(a,n) g(a,n) 中 [ f ( p − 1 , n % p + p ) − f ( n % p , n % p + p ) ] \left[ f(p-1,n\%p+p)-f(n\%p,n\%p+p) \right] [f(p−1,n%p+p)−f(n%p,n%p+p)] 在 n n n 为奇数情况下为 0 0 0
而对 g ( a , n ) g(a,n) g(a,n) 的一次拆分必定将 n n n 分成一奇一偶 , 所以最后 [ f ( p − 1 , n % p + p ) − f ( n % p , n % p + p ) ] \left[ f(p-1,n\%p+p)-f(n\%p,n\%p+p) \right] [f(p−1,n%p+p)−f(n%p,n%p+p)] 不为 0 0 0 的点的个数至多等于长度小于等于 log n \log n logn 的 01 串中不含有连续两个 1 作为子串的方案数 , 计算可以得到数量级为 f i b ( log n + 4 ) \mathrm{fib}(\log n+4) fib(logn+4) , 在题中所给数据限制下 f i b ( log n + 4 ) ≤ f i b ( 34 ) < 1 0 7 \mathrm{fib}(\log n+4) \leq \mathrm{fib}(34) < 10^7 fib(logn+4)≤fib(34)<107 , 复杂度满足
于是按如下式子计算
P ( S l , r ) = f ( l − 2 , n − m − 1 ) + f ( n − 1 , n − 1 ) − f ( r − 1 , n − 1 ) P(S_{l,r}) = f(l-2,n-m-1) + f(n-1,n-1) - f(r-1,n-1) P(Sl,r)=f(l−2,n−m−1)+f(n−1,n−1)−f(r−1,n−1)
其中 f ( n − 1 , n − 1 ) = f i b ( n ) f(n-1,n-1) = \mathrm{fib}(n) f(n−1,n−1)=fib(n)
相关文章:

2023辽宁省赛E
Solution 题目大致分为三个步骤 计算 P ( S ) P(S) P(S)证明删除区间连续且找到最值位置根据最值位置求出答案 接下来过程中不合法的组合数都默认为 0 0 0 第 1 步 - 求出总值 考虑 S m { 1 , 2 , ⋯ , m } S_m \{1, 2, \cdots, m\} Sm{1,2,⋯,m} , 则有 $P(S_{n2}…...

visual studio 启用C++11
用C11取决于你所使用的编译器和开发环境。以下是一些常见的编译器和相应的启用C11的方法: GCC (GNU Compiler Collection): 对于 GCC,你可以在编译时使用 -stdc11 或更高的标志来启用C11支持。例如: g -stdc11 yourfile.cpp -o yourprogramCl…...
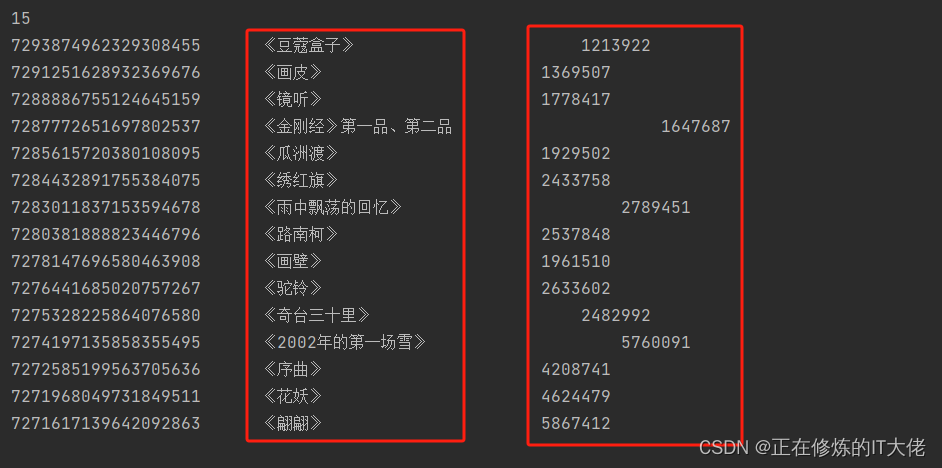
获取某个抖音用户的视频列表信息
思路 确定url确定并获取相关参数构造header发送请求解析数据输出数据 运行结果 代码 import requests # 获取某个用户的的视频信息,截至20231028,程序可以正常运行。 # 构造请求头header headers {User-Agent:..........................,Cookie:...…...
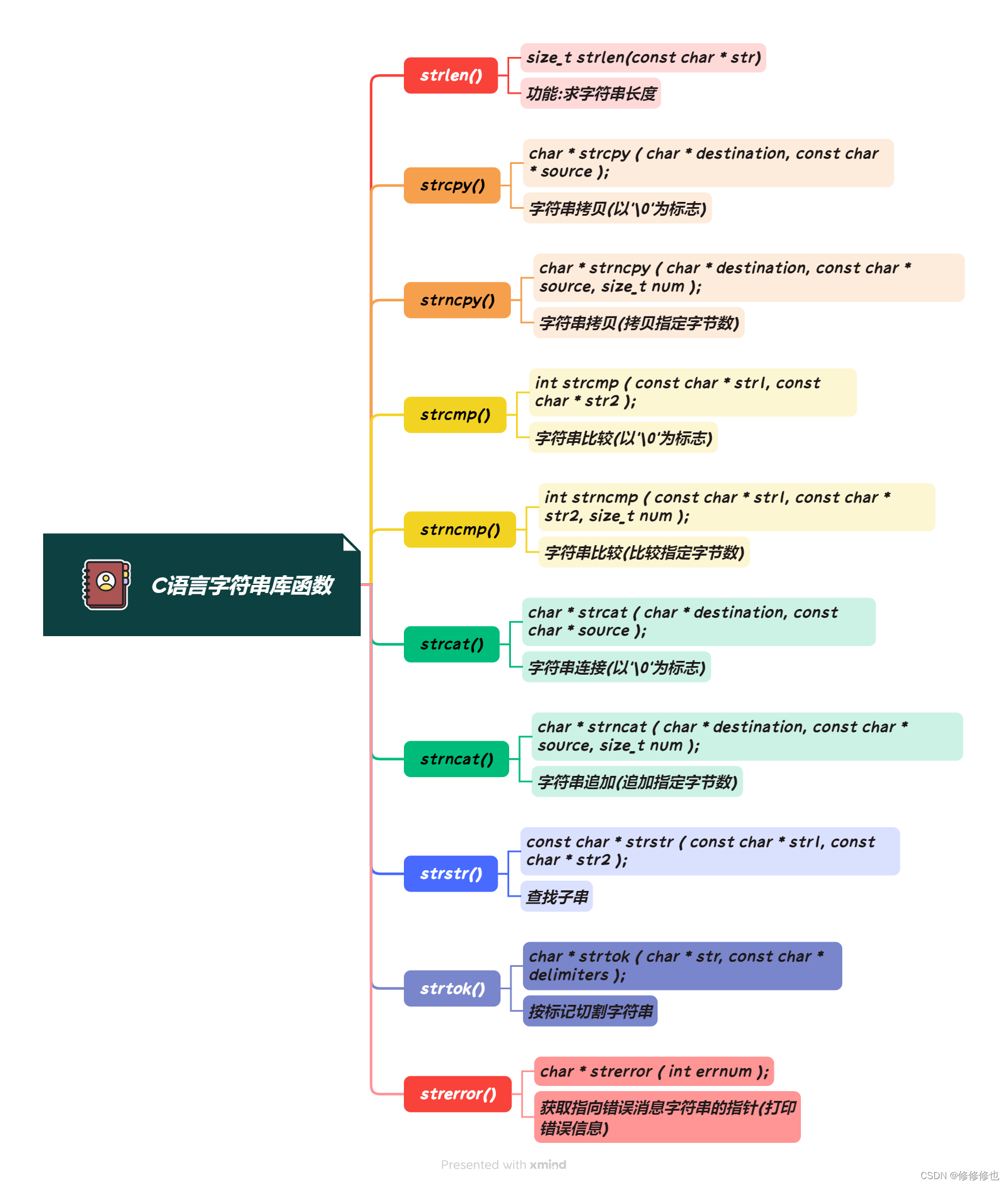
【C语言】strcpy()函数(字符串拷贝函数详解)
🦄个人主页:修修修也 🎏所属专栏:C语言 ⚙️操作环境:Visual Studio 2022 目录 一.strcpy()函数简介 1.函数功能 2.函数参数 1>.char * destination 2>.const char * source 3.函数返回值 4.函数头文件 二.strcpy()函数的具体使用 1.使用s…...

机器学习之IV编码,分箱WOE编码
IV的概念与作用 全称是Information Value,中文的意思是信息价值,或者信息量作用: 1、构建分类模型时,经常需要对特征进行筛选。 2、挑选特征的过程考虑的因素比较多,最主要和最直接的衡量标准是特征的预测能力&#…...

区块链技术与应用 【全国职业院校技能大赛国赛题目解析】第六套区块链系统部署与运维
第六套区块链系统部署与运维题目 环境 : ubuntu20 fisco : 2.8.0 子任务1-2-1: 搭建区块链系统并验证 题意: P2P起始端口 30500 channel起始端口 20500 JSONRPC 8945 使用Docker配置 使用 build_chain.sh 文件 进行生成节点文件 root@192-168-19-133:/yijiu/mode6# bas…...
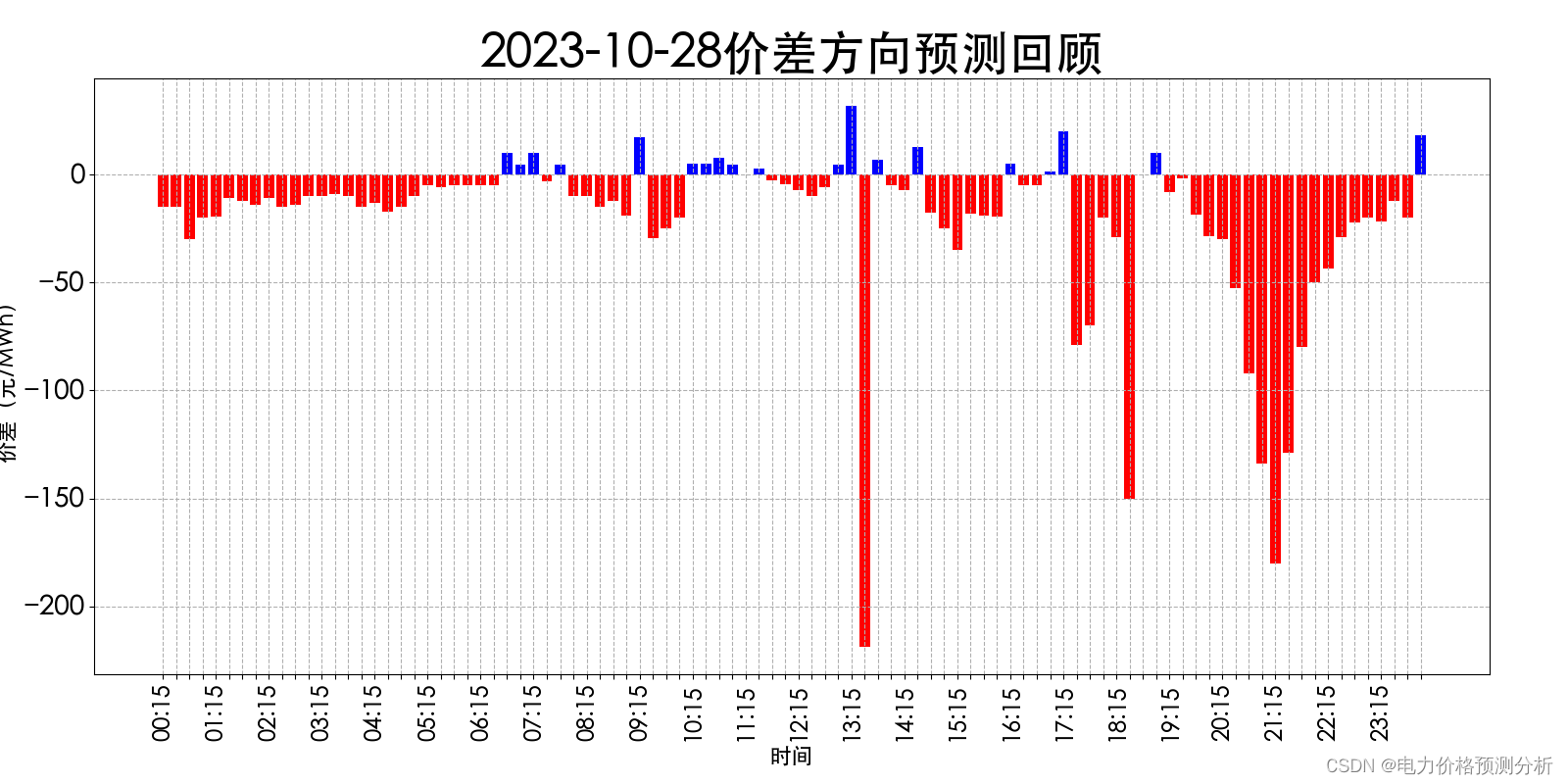
山西电力市场日前价格预测【2023-10-30】
日前价格预测 预测说明: 如上图所示,预测明日(2023-10-30)山西电力市场全天平均日前电价为309.35元/MWh。其中,最高日前电价为400.33元/MWh,预计出现在18:15。最低日前电价为0.00元/MWh,预计出…...
win10虚拟机安装教程
目录 1、安装VMware 10、12、16都可以,看个人选择 2、开始安装系统(以vm16为例) 3、在虚拟机中安装win10 完成 1、安装VMware 10、12、16都可以,看个人选择 下面链是我虚拟机安装包,需要可以下载。 YR云盘 软件安…...
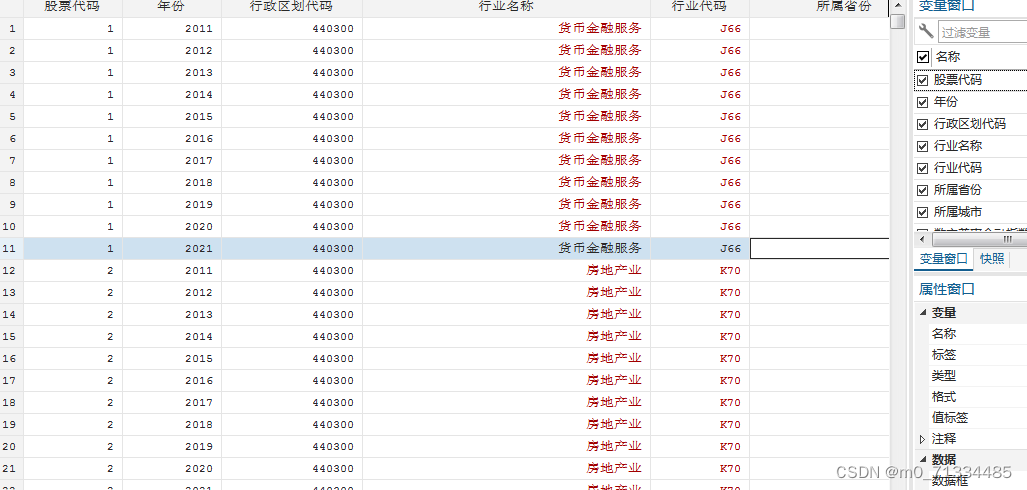
2011-2021年“第四期”数字普惠金融与上市公司匹配(根据城市匹配)/上市公司数字普惠金融指数匹配数据
2011-2021年“第四期”数字普惠金融与上市公司匹配(根据城市匹配)/上市公司数字普惠金融指数匹配数据 1、时间:2011-2021年 指标:指标:股票代码、年份、行政区划代码、行业名称、行业代码、所属省份、所属城市、数字…...

CSP-J 2023 T3 一元二次方程 解题报告
CSP-J 2023 T3 一元二次方程 解题报告 Link 前言 今年 C S P CSP CSP的原题, 回家 1 h 1h 1h内写 A C AC AC, 但是考场上没有写出来 , 原因是脑子太不好了, 竟然调了两个小时没有调出来. 一等奖悬那… 正题 看完题目,第一眼就是大模拟, 并且 C C F CCF CCF绝对不会让你好受…...
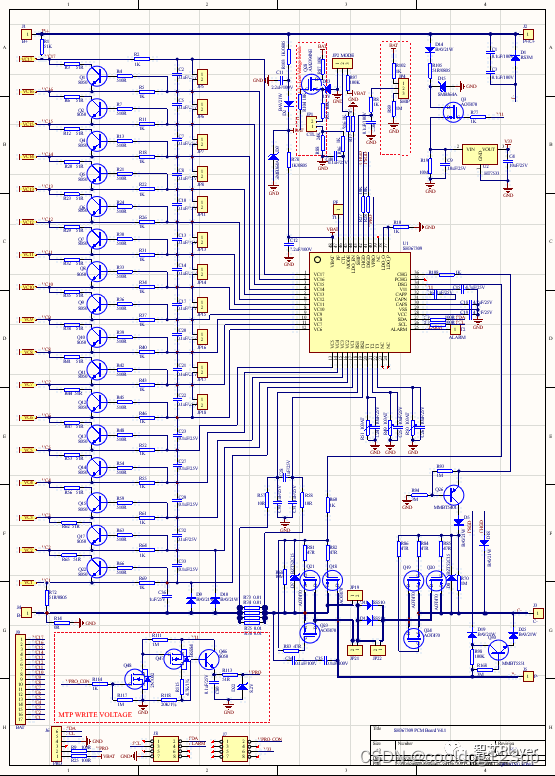
中颖单片机SH367309全套量产PCM,专用动力电池保护板开发资料
方案总体介绍 整套方案硬件部分共2块板子,包括MCU主板,采用SH79F6441-32作为主处理器。MCU主板包括2个版本。PCM动力电池保护板采用SH367309。 软件方案采用Keil51建立的工程,带蓝牙的版本,支持5~16S电池。 硬件方案--MCU主板 MC…...
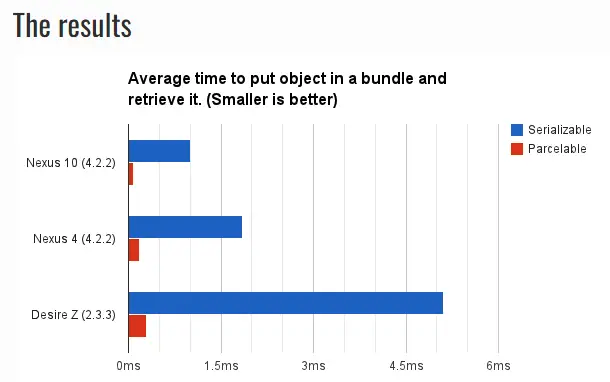
Android数据对象序列化原理与应用
序列化与反序列化 序列化是将对象转换为可以存储或传输的格式的过程。在计算机科学中,对象通常是指内存中的数据结构,如数组、列表、字典等。通过序列化,可以将这些对象转换为字节流或文本格式,以便在不同的系统之间进行传输或存…...

Linux cp命令:复制文件和目录
cp 命令,主要用来复制文件和目录,同时借助某些选项,还可以实现复制整个目录,以及比对两文件的新旧而予以升级等功能。 cp 命令的基本格式如下: [rootlocalhost ~]# cp [选项] 源文件 目标文件 选项: -a&…...

SpringBoot 接收不到 post 请求数据与接收 post 请求数据
文章归档:https://www.yuque.com/u27599042/coding_star/xwrknb7qyhqgdt10 SpringBoot 接收不到 post 请求数据 接收 post 请求数据,控制器方法参数需要使用 RequestParam 注解修饰 public BaseResponseResult<Object> getMailCode(RequestParam…...
vue3学习(十四)--- vue3中css新特性
文章目录 样式穿透:deep()scoped的原理 插槽选择器:slotted()全局选择器:global()动态绑定CSScss module 样式穿透:deep() 主要是用于修改很多vue常用的组件库(element, vant, AntDesigin),虽然配好了样式但是还是需要更改其他的样式就需要用…...

Python爬虫基础之Requests详解
目录 1. 简介2. 安装3. 发送请求4. 处理响应5. IP代理6. Cookie登录参考文献 原文地址:https://program-park.top/2023/10/27/reptile_4/ 本文章中所有内容仅供学习交流使用,不用于其他任何目的,严禁用于商业用途和非法用途,否则由…...

C++求根节点到叶子节点数字之和
文章目录 题目链接题目描述解题思路代码复杂度分析 题目链接 LCR 049. 求根节点到叶节点数字之和 - 力扣(LeetCode) 题目描述 给定一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表…...
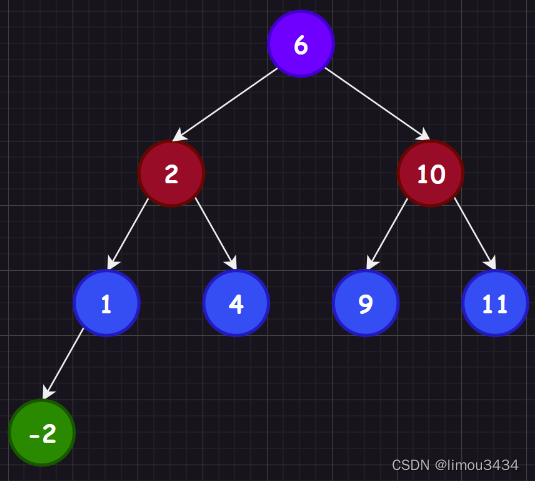
C++搜索二叉树
本章主要是二叉树的进阶部分,学习搜索二叉树可以更好理解后面的map和set的特性。 1.二叉搜索树概念 二叉搜索树的递归定义为:非空左子树所有元素都小于根节点的值,非空右子树所有元素都大于根节点的值,而左右子树也是二叉搜索树…...
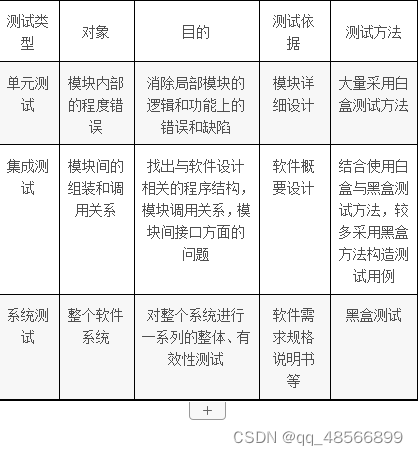
软件工程17-18期末试卷
2.敏捷开发提倡一个迭代80%以上的时间都在编程,几乎没有设计阶段。敏捷方法可以说是一种无计划性和纪律性的方法。错 敏捷开发是一种软件开发方法论,它强调快速响应变化、持续交付有价值的软件、紧密合作和适应性。虽然敏捷方法鼓励迭代开发和灵活性&…...
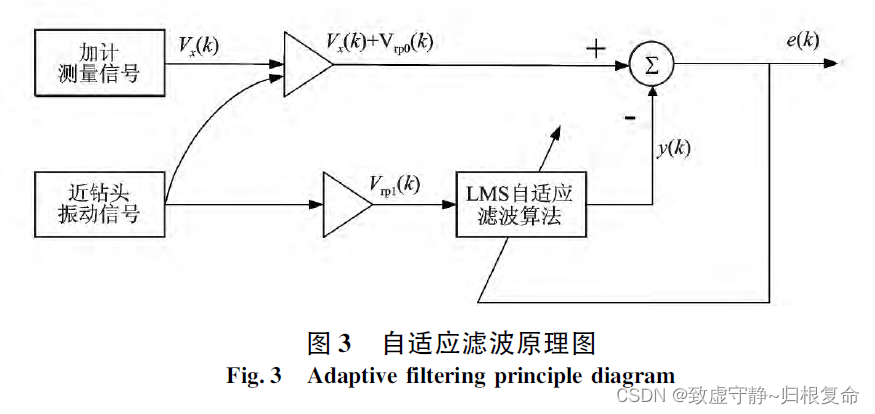
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
一、 引言 引言直接从原论文复制,大概看一下论文的关键点: 垂直导向钻井工具在近钻头振动和工具旋转的钻井工作状态下,工具姿态参数的动态测量精度不高。为此,通过理论分析和数值仿真,提出了转速补偿的算法以消除工具旋…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
