课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
一、 引言
引言直接从原论文复制,大概看一下论文的关键点:
垂直导向钻井工具在近钻头振动和工具旋转的钻井工作状态下,工具姿态参数的动态测量精度不高。为此,通过理论分析和数值仿真,提出了转速补偿的算法以消除工具旋转对测量的影响; 采用最小均方算法( Least Mean Square—LMS) 自适应滤波算法,可以有效滤除近钻头振动对测量的影响。数值仿真表明,经过转速补偿和LMS 自适应滤波后的井斜角测量误差可小于0. 1°,工具面角测量误差小于6°,有效地提高了垂直导向钻井工具的动态测量精度。
关键点:转速补偿的算法以消除工具旋转对测量的影响;用最小均方算法( Least Mean Square—LMS) 自适应滤波算法,可以有效滤除近钻头振动对测量的影响。
二、 动态测量中的问题
2.1 旋转运动对姿态测量的影响
在实际钻井过程中,设导向工具绕其回转中心以转速ω 旋转,则重力加速度计的工作状态如图1所示,图中R 为加速度计中心O’ 到工具回转中心O的距离。
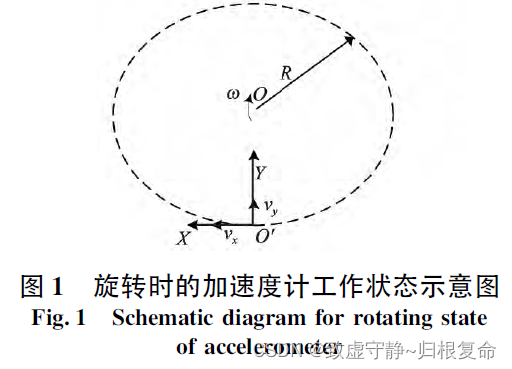
此时,X 轴 将会受到切向的附加惯性力作用,因此作用在X轴加速度计质量块的加速度 a x a_x ax不仅仅是重力加速度分量,还包括切向附加惯性力加速度。由加速度线性叠加原理得: a x = g x + α x = g s i n θ s i n φ + d ω d t R a_x=g_x+\alpha_x=gsin\theta sin\varphi +\frac{d\omega}{dt}R ax=gx+αx=gsinθsinφ+dtdωR
其中, g x g_x gx为X 轴重力加速度分量,单位为 m / s 2 m/s^2 m/s2 ; α x \alpha_x αx为X 轴所受到的切向附加惯性力加速度,单位为 m / s 2 m/s^2 m/s2,它与转速ω 的变化率成正比例; θ 为井斜角、φ 为工具面角。
Y 轴重力加速度计质量块也会因旋转而受到离心力作用,其加速度
a x = g x + α x = g s i n θ s i n φ + ω 2 R a_x=g_x+\alpha_x=gsin\theta sin\varphi +\omega^2R ax=gx+αx=gsinθsinφ+ω2R
其中, g y g_y gy为Y 轴重力加速度分量,单位为 m / s 2 m/s^2 m/s2; α x \alpha_x αx为Y轴所受到的离心力加速度,单位为 m / s 2 m/s^2 m/s2,它与转速平方成正比。由上面两个公式可知,当工具转速较高时,安装在导向工具上的重力加速度计在井眼的不同方位上将产生差异较大的测量信号,从而导致工具姿态的较大测量误差。
2.2 近钻头振动对姿态测量的影响
在正常钻进过程中,钻头切削岩石会使钻柱产生横向和纵向振动,且横向振动尤为明显。近钻头振动信号有3 大特性:
①牙轮钻头牙齿吃入岩石形成高频特性;
②近钻头震源具有宽频性;
③钻头牙齿、牙轮与钻头整体复合运动具有随机性。
近钻头振动信号的幅值一般在10g左右( g 为重力加速度, g = 0.9 m / s 2 g=0.9m/s^2 g=0.9m/s2 ) ,最大可达到30g。因此,近钻头的振动加速度一般远大于重力加速度,弱小的重力加速度信号将湮灭在振动加速度噪声中,导致工具姿态测量无效。根据近钻头横向振动信号特性,采用幅值为6 g 的随机白噪声来模拟近钻头高频随机振动信号,信号特征如下图所示。
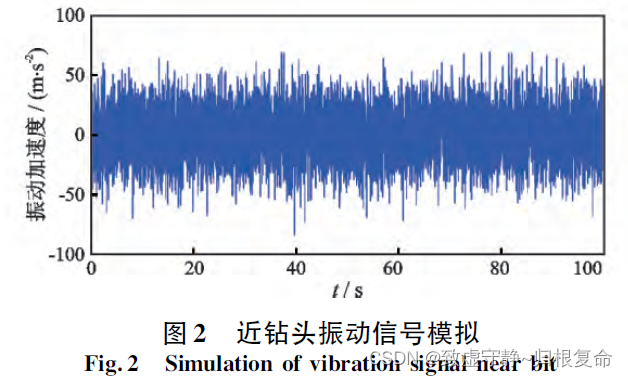
设仅考虑近钻头处的横向振动,其对X、Y 轴向分解后分别记为Ax、Ay,设 A x = K x g A_x=K_xg Ax=Kxg, A y = K y g A_y=K_yg Ay=Kyg; K x 、 K y K_x、K_y Kx、Ky为最大值为10 的随机系数。假设近钻头振动、旋转运动以及重力加速度对加速度计的影响线性可加,则X,Y 轴重力加速度计的测量信号为 V ^ x = V x + V r x + V p x = V g s i n θ s i n φ + V g R g d ω d t + K x V g \hat{V}_x=V_x+V_{rx}+V_{px}=V_gsin\theta sin\varphi +V_g\frac{R}{g}\frac{d\omega}{dt}+K_xV_g V^x=Vx+Vrx+Vpx=Vgsinθsinφ+VggRdtdω+KxVg
V ^ y = V y + V r y + V p y = V g s i n θ c o s φ + V g R g ω 2 + K y V g \hat{V}_y=V_y+V_{ry}+V_{py}=V_gsin\theta cos\varphi +V_g\frac{R}{g}\omega^2+K_yV_g V^y=Vy+Vry+Vpy=Vgsinθcosφ+VggRω2+KyVg
其中: V x 、 V y V_x、V_y Vx、Vy为加速度计的理想输出信号; V r x 、 V r y V_{rx}、V_{ry} Vrx、Vry分别为X、Y 轴加速度计的旋转附加信号; V p x 、 V p y V_{px}、V_{py} Vpx、Vpy为振动产生的附加信号。
三、导向工具姿态动态测量方法
3.1 工具旋转转速补偿算法
考虑到工具旋转时的附加信号 V r x 、 V r y V_{rx}、V_{ry} Vrx、Vry为转速ω的函数,因此,利用速率陀螺仪实时测出工具转速ω,则可进行误差校正。
设由速率陀螺仪测得导向工具转速为 ω ^ \hat{\omega} ω^( 考虑速率陀螺仪的测量误差为5%) ,可计算得工具旋转附加信号估计值为 V ^ r x 、 V ^ r y \hat{V}_{rx}、\hat{V}_{ry} V^rx、V^ry利用2.2节的公式进行校正: V ^ x 1 = V ^ x − V ^ r x = V x + V p x \hat{V}_{x1}=\hat{V}_{x}-\hat{V}_{rx}=V_x+V_{px} V^x1=V^x−V^rx=Vx+Vpx
V ^ y 1 = V ^ y − V ^ r y = V y + V p y \hat{V}_{y1}=\hat{V}_{y}-\hat{V}_{ry}=V_y+V_{py} V^y1=V^y−V^ry=Vy+Vpy
3.2 振动信号的自适应滤波
近钻头振动信号是一种宽带噪声信号,自适应滤波器利用其自动调节参数的优势,无需知道输入信号和噪声统计特性,自动跟踪噪声源,将噪声滤除。自适应滤波的基本思想是: 将振动信号与滤波估计出的参考信号进行抵消操作。
自适应滤波器有两路输入:
一路为原始通道,其不仅接收加速度计测量信号 V x ( k ) V_x(k) Vx(k)( 将加速度传感器测量信号离散化) ,还接收和信号 V x ( k ) V_x(k) Vx(k)不相关的近钻头振动附加信号 V r p 0 ( k ) V_{rp0}(k) Vrp0(k)
另一路为参考输入通道,其接收与信号 V x ( k ) V_x(k) Vx(k)不相关且与振动信号 V r p 0 ( k ) V_{rp0}(k) Vrp0(k)相关的振动信号 V r p 1 V_{rp1} Vrp1
自适应滤波器原理图结构如下所示:
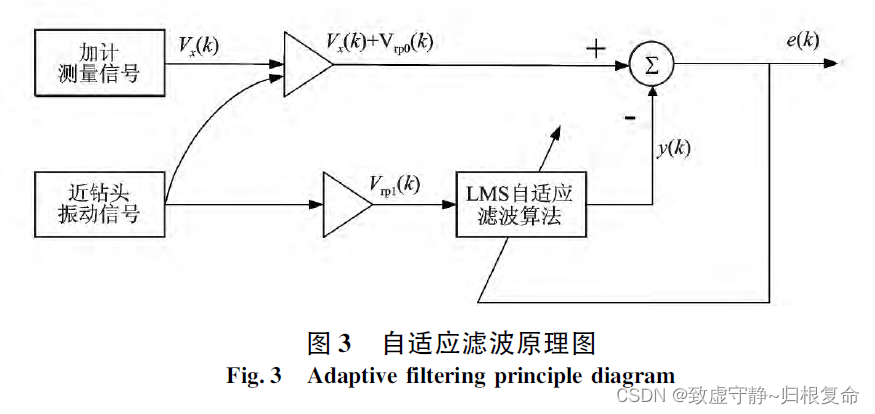
根据自适应滤波器的特性,振动信号 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)经过LMS自适应滤波器自动调整输出后,得到 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)的估计信号,即 y ( k ) = V ^ r p 1 ( k ) y(k)=\hat{V}_{rp1}(k) y(k)=V^rp1(k).
则自适应滤波器系统输出的误差信号e( k) 等于原始信号和参考输入信号的差值,表示为: e ( k ) = V x ( k ) + V r p 0 ( k ) − V ^ r p 1 ( k ) e(k)=V_x(k)+V_{rp0}(k)-\hat{V}_{rp1}(k) e(k)=Vx(k)+Vrp0(k)−V^rp1(k)
对这个式子做一个变形: e ( k ) − V x ( k ) = V r p 0 ( k ) − V ^ r p 1 ( k ) e(k)-V_x(k)=V_{rp0}(k)-\hat{V}_{rp1}(k) e(k)−Vx(k)=Vrp0(k)−V^rp1(k)
并且对上面的两边同时开平方并取均方误差: E [ e 2 ( k ) ] = E [ V x 2 ( k ) ] + E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] + 2 E [ V x ( K ) ( V r p ( k ) − V r p 1 ( k ) ) ] E[e^2(k)]=E[{V_x}^2(k)]+E[(V_{rp0}(k)-V_{rp1}(k))^2]+2E[V_x(K)(V_{rp}(k)-V_{rp1}(k))] E[e2(k)]=E[Vx2(k)]+E[(Vrp0(k)−Vrp1(k))2]+2E[Vx(K)(Vrp(k)−Vrp1(k))]
E [ e 2 ( k ) ] E[e^2(k)] E[e2(k)]表示功率信号, V x ( k ) V_x(k) Vx(k)与 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)无关,所以 2 E [ V x ( K ) ( V r p ( k ) − V r p 1 ( k ) ) ] = 0 2E[V_x(K)(V_{rp}(k)-V_{rp1}(k))]=0 2E[Vx(K)(Vrp(k)−Vrp1(k))]=0,因此, 均方误差 E [ e 2 ( k ) ] E[e^2(k)] E[e2(k)] 最小, 等价于 E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] E[(V_{rp0}(k)-V_{rp1}(k))^2] E[(Vrp0(k)−Vrp1(k))2]达到最小。
LMS 自适应滤波过程是由其权向量迭代公式: W ( k + 1 ) = W ( k ) + 2 μ e ( k ) x ( k ) W(k+1)=W(k)+2\mu e(k)x(k) W(k+1)=W(k)+2μe(k)x(k)
自身调节权值 W ( k ) W(k) W(k)使得 E [ e 2 ( k ) ] E[e^2(k)] E[e2(k)]达到最小。
式中: μ \mu μ为调整搜索步长的正值常数,其收敛速度与系统稳定性有关; W ( k ) W(k) W(k)为系统第k 次迭代权系数; x ( k ) x(k) x(k)为输入信号。
根据 e ( k ) − V x ( k ) = V r p 0 ( k ) − V ^ r p 1 ( k ) e(k)-V_x(k)=V_{rp0}(k)-\hat{V}_{rp1}(k) e(k)−Vx(k)=Vrp0(k)−V^rp1(k),所以在LMS 准则下, E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] E[(V_{rp0}(k)-V_{rp1}(k))^2] E[(Vrp0(k)−Vrp1(k))2]被最小化的同时, E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] E[(V_{rp0}(k)-{V}_{rp1}(k))^2] E[(Vrp0(k)−Vrp1(k))2]也被最小化了,即LMS 自适应滤波器的输出 y ( k ) y(k) y(k) 向 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)逼近等效于 e ( k ) e(k) e(k) 向 V x ( k ) V_x(k) Vx(k) 逼近,从而系统输出的是加速度计信号 V x ( k ) V_x(k) Vx(k)的最佳估计。
剩下的内容为效果仿真了,具体就不再看了,论文整体上思路很简单,也好理解,细心看一下就好,而且本篇论文实际稍微有点远,为2016的论文,有兴趣的可以从知网下载。
四、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
相关文章:

课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
一、 引言 引言直接从原论文复制,大概看一下论文的关键点: 垂直导向钻井工具在近钻头振动和工具旋转的钻井工作状态下,工具姿态参数的动态测量精度不高。为此,通过理论分析和数值仿真,提出了转速补偿的算法以消除工具旋…...

阿里云服务器—ECS快速入门
这里对标阿里云的课程,一步步学习,链接在下面,学习完考试及格即可获取阿里云开发认证和领取证书,大家可以看看这个,这里我当作笔记,记一下提升印象! 内容很长,请耐心看完࿰…...

Hive简介及核心概念
本专栏案例数据集链接: https://download.csdn.net/download/shangjg03/88478038 1.简介 Hive 是一个构建在 Hadoop 之上的数据仓库,它可以将结构化的数据文件映射成表,并提供类 SQL 查询功能,用于查询的 SQL 语句会被转化为 MapReduce 作业,然后提交到 Hadoop 上运行。 …...

CrossOver 23.6.0 虚拟机新功能介绍
CrossOver 23.6.0 Mac 此应用程序允许您运行为 Microsoft Windows 编写的程序,而无需实际安装操作系统。 CrossOver 23.6.0 Mac 包括一个 Windows 程序库,用于它可以运行的 Windows 程序。 您会发现非常流行的应用程序,例如 Microsoft Word…...
(免费领源码)Java#Springboot#mysql农产品销售管理系统47627-计算机毕业设计项目选题推荐
摘 要 随着互联网趋势的到来,各行各业都在考虑利用互联网将自己推广出去,最好方式就是建立自己的互联网系统,并对其进行维护和管理。在现实运用中,应用软件的工作规则和开发步骤,采用Java技术建设农产品销售管理系统。…...

centos更改yum源
1、更改yum源 阿里云/etc/yum.repos.d/CentOS-Base.repo 金山云/etc/yum.repos.d/cloud.repo vi /etc/yum.repos.d/cloud.repo 替换为 [base] nameCentOS-$releasever - Base mirrorlisthttp://mirrorlist.centos.org/?release$releasever&arch$basearch&repoos&…...
React-快速搭建开发环境
1.安装 说明:react-excise-01是创建的文件名 npx create-react-app react-excise-01 2. 打开文件 说明:we suggest that you begin by typing:下面即是步骤。 cd react-excise-01 npm start 3.显示...

算法随想录算法训练营第四十六天| 583. 两个字符串的删除操作 72. 编辑距离
583. 两个字符串的删除操作 题目:给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 思路:这题思路主要是求出 word1 字符串和 word2 字符串中的最长相同的子字符串&…...
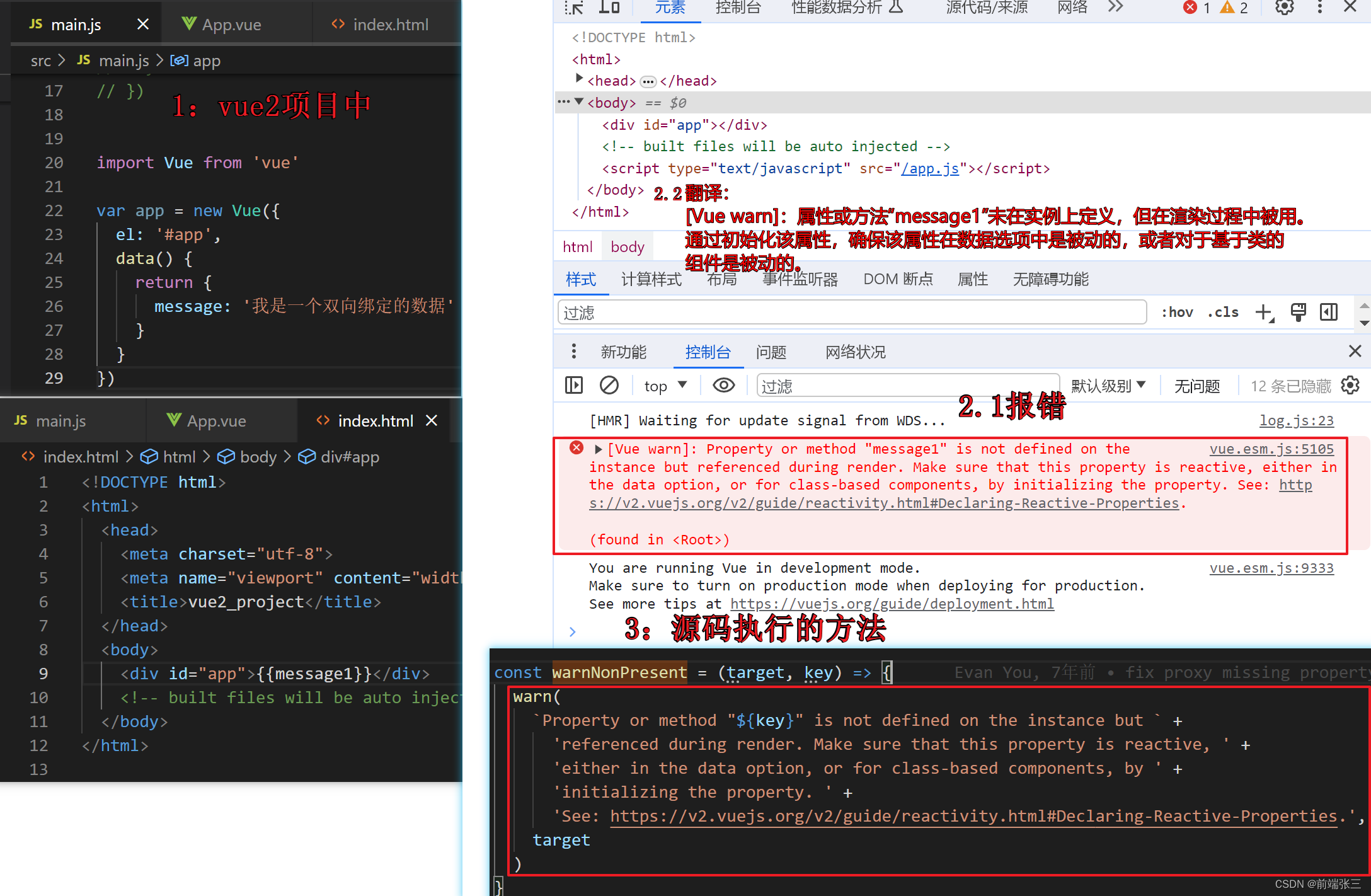
vue源码分析(五)——vue render 函数的使用
文章目录 前言一、render函数1、render函数是什么? 二、render 源码分析1.执行initRender方法2.vm._c 和 vm.$createElement 调用 createElement 方法详解(1)区别(2)代码 3、原型上的_render方法(1…...

Maven第三章:IDEA集成与常见问题
Maven第三章:IDEA集成与常见问题 前言 本章内容重点:了解如何将Maven集成到IDE(如IntelliJ IDEA或Eclipse)中,以及使用过程中遇到的常见的问题、如何解决,如何避免等,可以大大提高开发效率。 IEAD导入Maven项目 File ->Open 选择上一章创建的Maven项目 my-app查看po…...

数据结构—线性实习题目(二)5迷宫问题(栈)
迷宫问题(栈) #include <iostream> #include <assert.h> using namespace std;int qi1, qi2; int n; int m1, p1; int** Maze NULL; int** mark NULL;struct items {int x, y, dir; };struct offsets {int a, b;char* dir; };const int…...
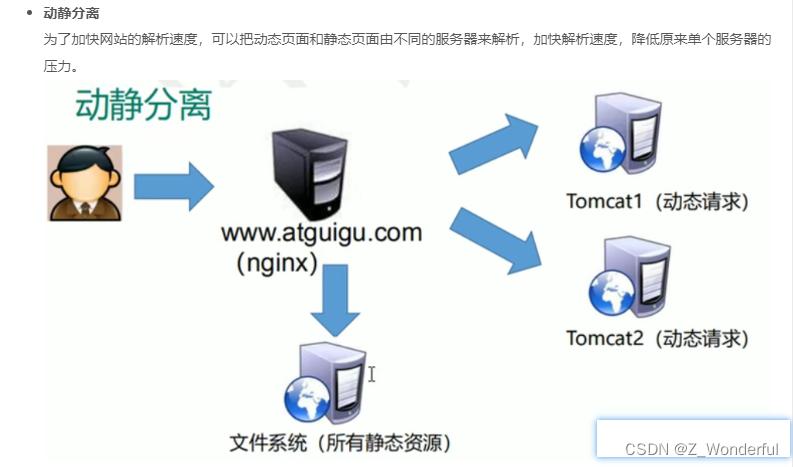
Nginx 的配置文件(负载均衡,反向代理)
Nginx可以配置代理多台服务器,当一台服务器宕机之后,仍能保持系统可用。 cmd查找端口是否使用:netstat -ano Nginx出现403 forbidden #解决办法:修改web目录的读写权限,或者是把nginx的启动用户改成目录的所属用户&…...
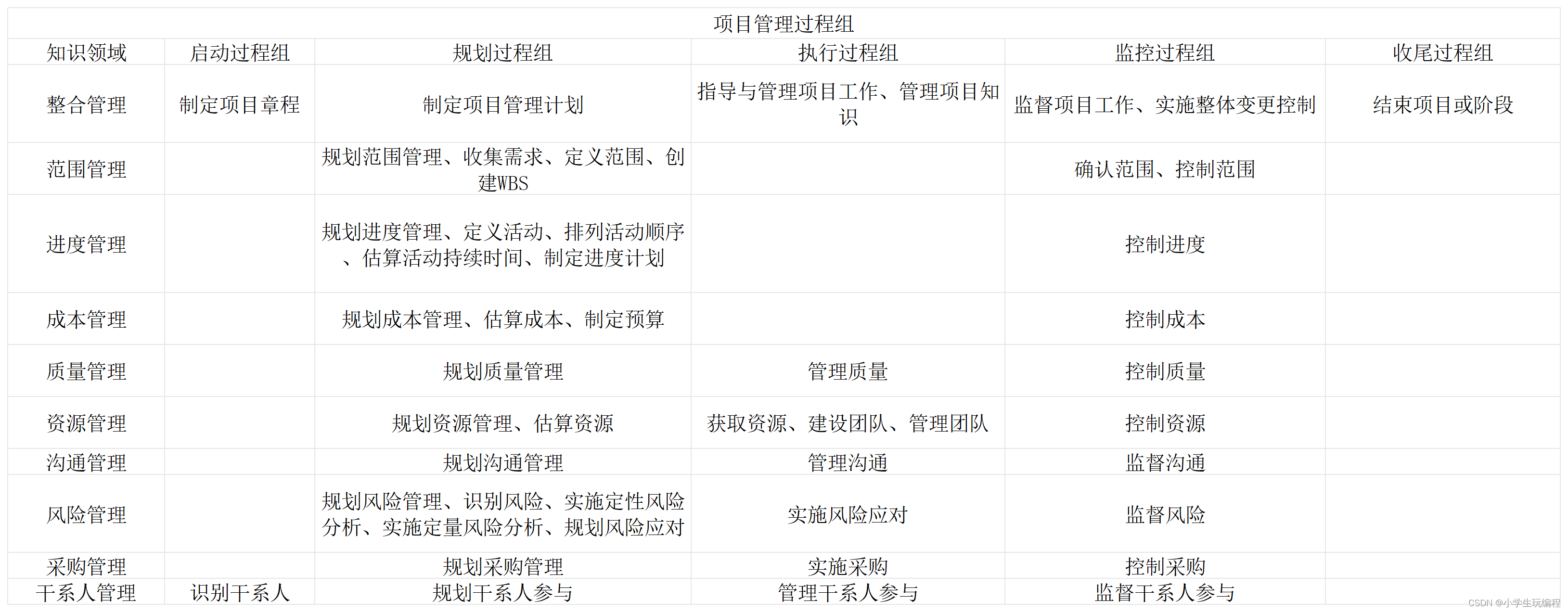
项目管理49个过程定义与作用、五大过程组
五大过程组: 49个过程的定义与作用: 1.整合管理: (1)制定项目章程:制定项目章程是编写一份正式批准项目并授予项目经理权力的文件的过程,其作用是①确立组织与项目的关系;②展示组织对项目的承诺ÿ…...

MySQL篇---第六篇
系列文章目录 文章目录 系列文章目录一、 MySQL 中 varchar 与 char 的区别?varchar(30) 中的 30代表的涵义?二、 int(11) 中的 11 代表什么涵义?三、为什么 SELECT COUNT(*) FROM table 在 InnoDB 比MyISAM 慢?一、 MySQL 中 varchar 与 char 的区别?varchar(30) 中的 30…...
QA新人入职任务
一、背景 分享记录一下入职新公司后,新人第一周接到的新手任务,回顾总结,方便自己成长和思考~ 二、新人任务说明 题目1:接口相关 题目2:UI相关 UI原型图 三、任务要求 1、根据题目2原型图,进行UI测试…...

更新电脑显卡驱动的操作方法有哪些?
更新显卡驱动可以有效的提升我们电脑的性能,可以通过设备管理器、显卡驱动软件等方式进行检查驱动是否需要更新,并修复一些电脑上已知的显卡问题。 然而,对于一些不是很懂电脑技术的人员来说,更新电脑显卡驱动是一件比较复杂和混乱…...
[Docker]三.Docker 部署nginx,以及映射端口,挂载数据卷
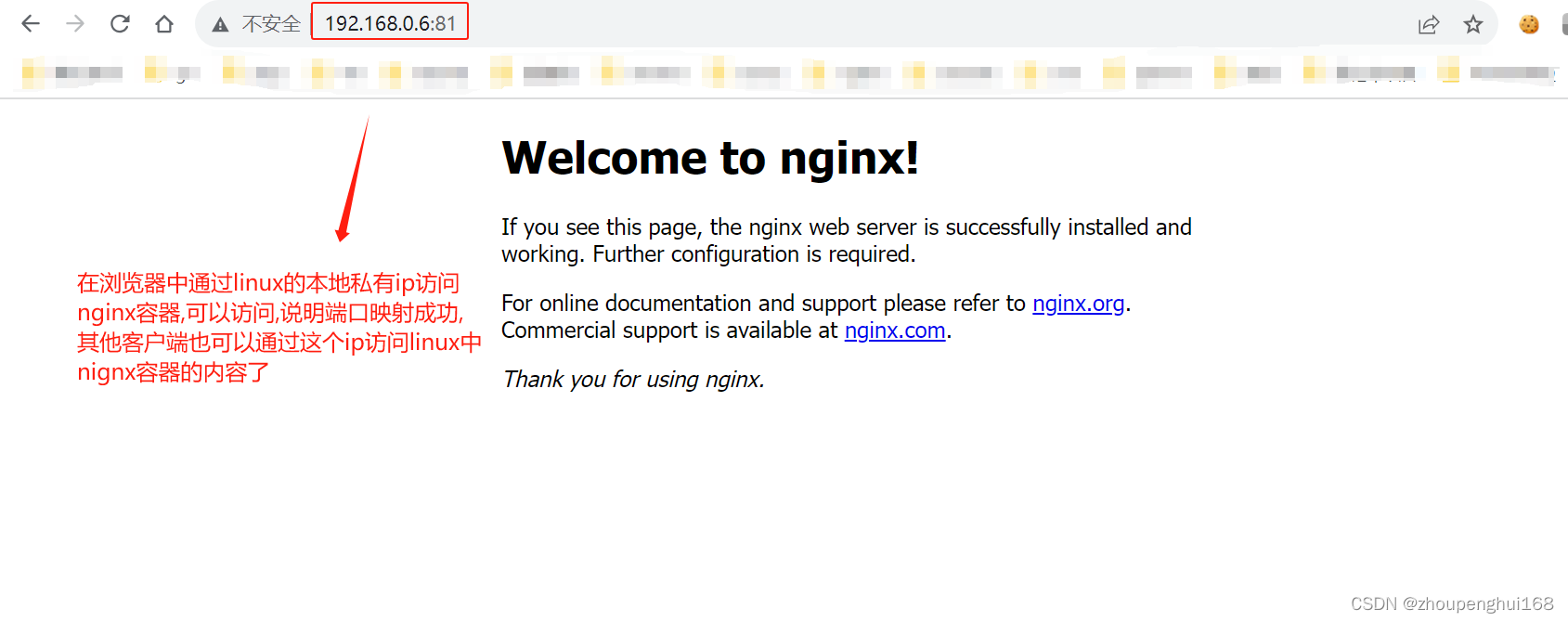
一.Docker 部署 Nginx 以及端口映射 Docker 部署 Nginx,首先需要下载nginx镜像,然后启动这个镜像,就运行了一个nginx的容器了 1.下载 nginx 镜像并启动容器 #查看是否存在nginx镜像:发现没有nginx镜像 [rootlocalhost zph]# docker images | grep nginx#下载nginx镜像 [rootl…...

【0基础学Java第三课】-- 运算符
3. 运算符 3.1 什么是运算符3.2 算术运算符3.2.1 **基本四则运算符:加减乘除模( - * / %)**3.2.2 增量运算符 - * %3.2.3 自增/自减运算符 -- 3.3 关系运算符3.4逻辑运算符(重点)3.4.1 逻辑与 &&3.4.2 逻辑 ||3.4.3逻辑非 !3.4.4 短路求值 3.5 …...
unocss和tailwindcss css原子引擎
第一种tailwindcss: tailwindcss官网 https://tailwindcss.com/docs/grid-column 基本介绍及优点分析 Tailwind CSS 中文文档 - 无需离开您的HTML,即可快速建立现代网站 PostCss 处理 Tailwind Css 基本流程 PostCSS - 是一个用 JavaScript 工具和插…...

HIT_OS_LAB1 调试分析 Linux 0.00 引导程序
操作系统实验一 姓名:董帅学号:2021111547班级:21R0312 1.1 实验目的 熟悉实验环境掌握如何手写Bochs虚拟机的配置文件掌握Bochs虚拟机的调试技巧掌握操作系统启动的步骤 1.2 实验内容 1.2.1 掌握如何手写Bochs虚拟机的配置文件 boot: f…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
