基于水循环算法的无人机航迹规划-附代码
基于水循环算法的无人机航迹规划
文章目录
- 基于水循环算法的无人机航迹规划
- 1.水循环搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用水循环算法来优化无人机航迹规划。
1.水循环搜索算法
水循环算法原理请参考:https://blog.csdn.net/u011835903/article/details/108549079
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得水循环搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用水循环算法对航迹评价函数式(7)进行优化。优化结果如下:

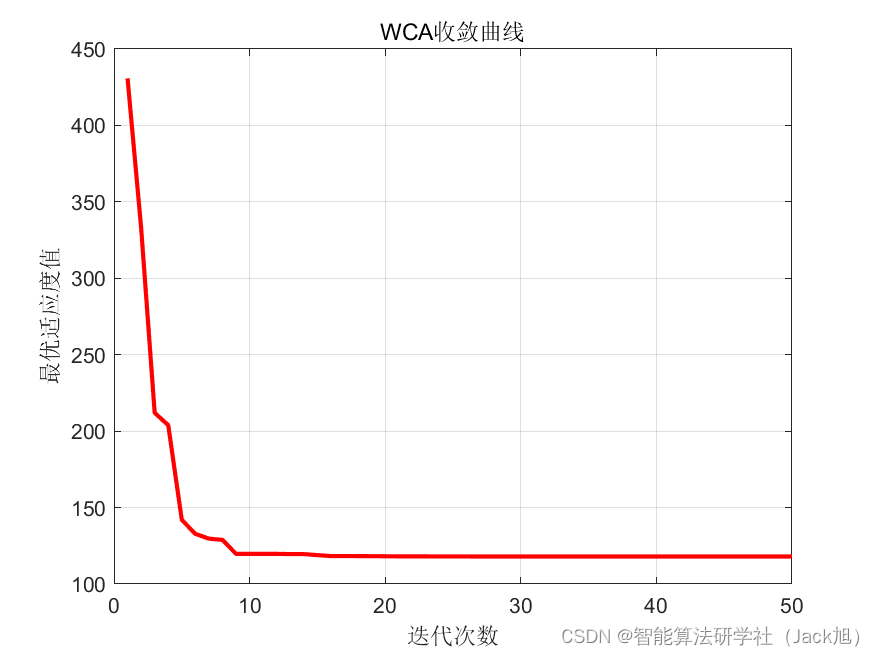
从结果来看,水循环算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于水循环算法的无人机航迹规划-附代码
基于水循环算法的无人机航迹规划 文章目录 基于水循环算法的无人机航迹规划1.水循环搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用水循环算法来优化无人机航迹规划。 1.水循环…...
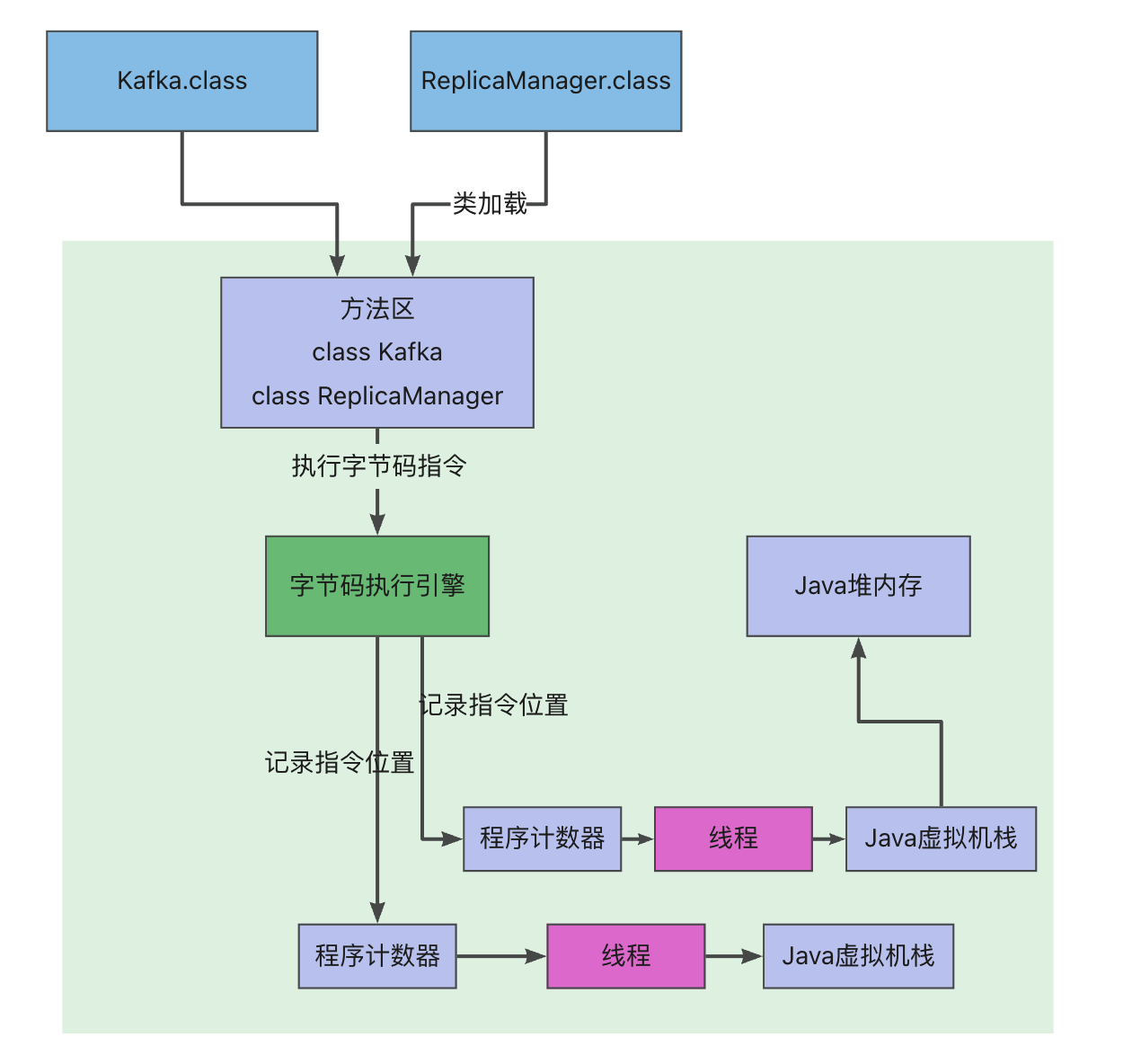
JVM调优(10)JVM的运行时数据区
一、概述 对于 C C 来说,在内存管理领域,JVM既拥有最高的权利,但是同时他们又是从事最基础工作的劳动人员,因为他们担负着每一个对象从开始到结束的维护责任。而对于Java来说,再虚拟机自动内存管理的帮助下࿰…...

Python网络爬虫介绍
视频版教程:一天掌握python爬虫【基础篇】 涵盖 requests、beautifulsoup、selenium 什么是网络爬虫? 网络爬虫(又称为网页蜘蛛,网络机器人,在FOAF社区中间,更经常的称为网页追逐者)ÿ…...

iOS QR界面亮度调整
亮度调事,不久在QR界面切换的时候还要考虑进入前台后台时的操作 1.QR界面功能实现代码。 QR界面- (void)viewWillAppear:(BOOL)animated {[super viewWillAppear:animated];[[NSUserDefaults standardUserDefaults] setValue:([UIScreen mainScreen].brightness) …...
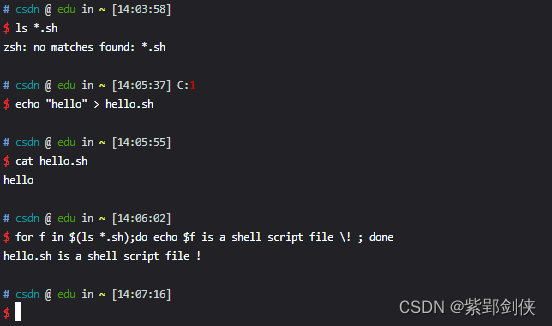
Linux shell编程学习笔记17:for循环语句
Linux Shell 脚本编程和其他编程语言一样,支持算数、关系、布尔、字符串、文件测试等多种运算,同样也需要进行根据条件进行流程控制,提供了if、for、while、until等语句。 之前我们探讨了if语句,现在我们来探讨for循环语句。 Li…...

Go语言用Resty库编写的音频爬虫代码
目录 一、Go语言与Resty库简介 二、音频爬虫的实现 1、确定抓取目标 2、使用Resty发送HTTP请求 3、解析响应数据 4、下载音频文件 5、并发下载音频文件 三、注意事项 总结 随着互联网的飞速发展,网络爬虫逐渐成为数据获取和分析的重要工具。在音频领域&…...

AWTK 液体流动效果控件发布
液体流动效果控件。 主要特色: 支持水平和垂直方向。支持正向和反向流动。支持设置头尾的图片。支持设置流动的图片。支持设置速度的快慢。支持启停操作。 准备 获取 awtk 并编译 git clone https://github.com/zlgopen/awtk.git cd awtk; scons; cd -运行 生成…...

对mysql的联合索引的深刻理解
背景 对mysql的联合索引的考察是Java程序员面试高频考点!必须深刻理解掌握否则容易丢分非常可惜。 技术难点 考察对最左侧匹配原理理解。 原理 暂且不表。网上讲这非常多。我理解就是,B树每个非叶子节点的值都是有序存放索引的值。 比如对A、B、C …...
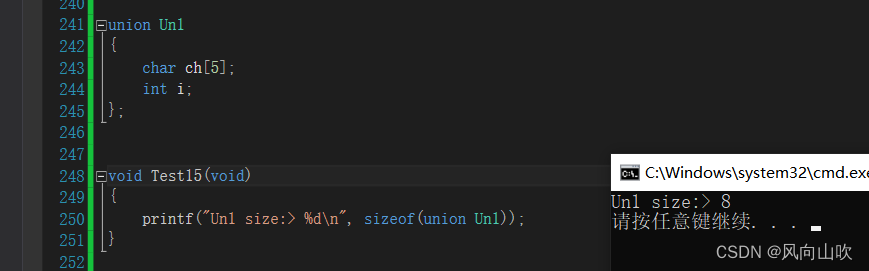
C的自定义类型
目录 1. 结构体 1.1. 结构体类型的声明 1.1.1. 特殊声明 2. 结构的自引用 3. 结构体变量的定义和初始化 4. 结构体内存对齐 4.1. 结构体内存对齐 4.2. 修改默认对齐数 5. 结构体传参 6. 结构体实现位段(位段的填充&可移植性) 6.1. 什么是位…...

我的创作纪念日 - 2048
机缘 昨天刚刚收到 C 站的 1024 勋章: 今天爬山途中就又收到了 CSDN 的创作 2048 天纪念推送: 虽然 1024、2048 这些数字对普通人来说可能没有意义,但对于程序员来说却有不一样的情结。感谢 C 站这波细心的操作,替程序员的我们记…...
拿捏面试官,高频接口自动化测试面试题总结(附答案)狂收offer...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 面试题࿱…...
大数据-Storm流式框架(六)---Kafka介绍
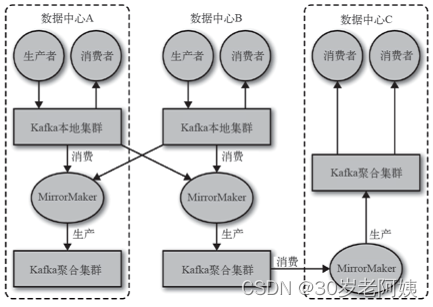
Kafka简介 Kafka是一个分布式的消息队列系统(Message Queue)。 官网:Apache Kafka 消息和批次 kafka的数据单元称为消息。消息可以看成是数据库表的一行或一条记录。 消息由字节数组组成,kafka中消息没有特别的格式或含义。 消息有可选的键&#x…...

自动驾驶的未来展望和挑战
自动驾驶技术是一项引人瞩目的创新,将在未来交通领域产生深远影响。然而,随着技术的不断演进,自动驾驶也面临着一系列挑战和障碍。本文将探讨自动驾驶的未来发展方向、技术面临的挑战,以及自动驾驶对社会和环境的潜在影响。 自动驾…...

2.11、自定义图融合过程与量化管线
introduction 介绍如何自定义量化优化过程,以及如何手动调用优化过程 code from typing import Callable, Iterableimport torch import torchvisionfrom ppq import (BaseGraph, QuantizationOptimizationPass,QuantizationOptimizationPipeline, QuantizationSetting,Tar…...

Linux——文件权限属性和权限管理
文件权限属性和权限管理 本章思维导图: 注:本章思维导图对应的Xmid文件和.png文件都以传到“资源” 文章目录 文件权限属性和权限管理1. sudo提权和sudoers文件1.1 sudo提权和成为root的区别 2. 权限2.1 Linux群体2.1.1 为什么要有所属组2.1.2 修改文件…...
数组与链表算法-单向链表算法
目录 数组与链表算法-单向链表算法 C代码 单向链表插入节点的算法 C代码 单向链表删除节点的算法 C代码 对单向链表进行反转的算法 C代码 单向链表串接的算法 C代码 数组与链表算法-单向链表算法 在C中,若以动态分配产生链表节点的方式,则可以…...

Oracle(6) Control File
一、oracle控制文件介绍 1、ORACLE控制文件概念 Oracle控制文件是Oracle数据库的一个重要元素,用于记录数据库的结构信息和元数据。控制文件包含了数据库的物理结构信息、数据字典信息、表空间和数据文件的信息等。在Oracle数据库启动时,控制文件会被读…...
吴恩达《机器学习》2-5->2-7:梯度下降算法与理解
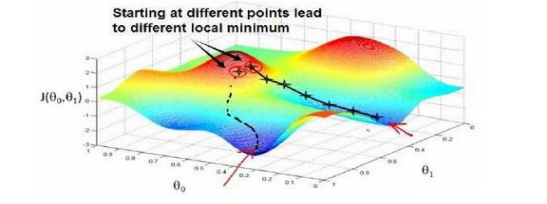
一、梯度下降算法 梯度下降算法的目标是通过反复迭代来更新模型参数,以便最小化代价函数。代价函数通常用于衡量模型的性能,我们希望找到使代价函数最小的参数值。这个过程通常分为以下几个步骤: 初始化参数: 随机或设定初始参数…...
方法)
Pytorch detach()方法
detach() 是 PyTorch 中的一个方法,用于从计算图中分离(detach)张量。它可以将一个张量从当前计算图中分离出来,返回一个新的张量,该张量与原始张量共享相同的底层数据,但不再追踪梯度信息。 当你需要在计…...
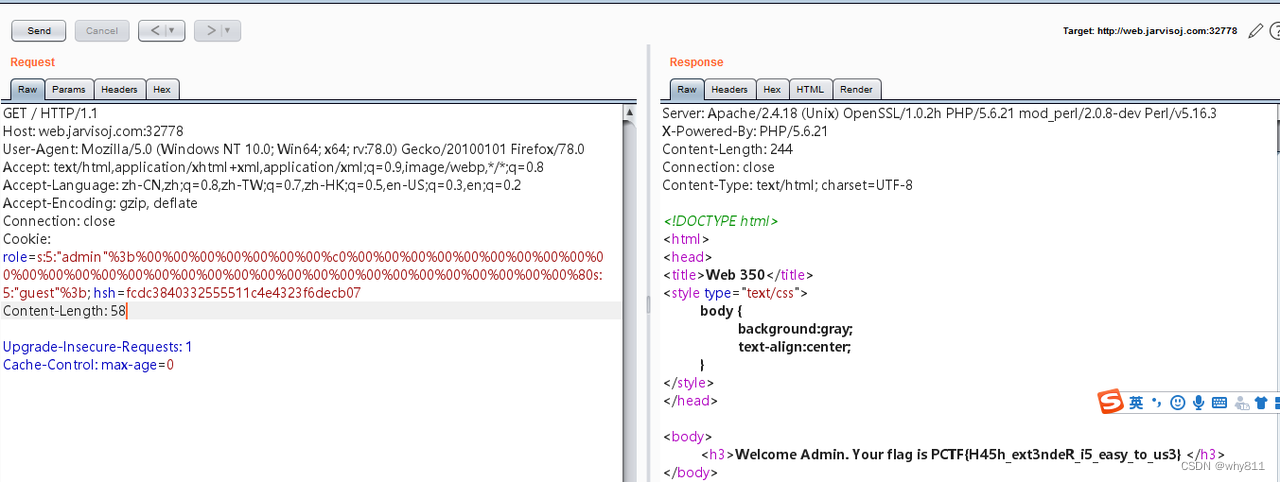
CTF-php特性绕过
注意:null0 正确 nullflase 错误 Extract变量覆盖 <?php$flagxxx; extract($_GET);if(isset($shiyan)){ $contenttrim(file_get_contents($flag));//trim移除引号if($shiyan$content){ echoctf{xxx}; }else{ echoOh.no;} }?> extract() 函数从数组中将…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
