RL笔记:动态规划(2): 策略迭代
目录
0. 前言
(4.3) 策略迭代
Example 4.2: Jack’s Car Rental
Exercise 4.4
Exercise 4.5
Exercise 4.6
Exercise 4.7
0. 前言
Sutton-book第4章(动态规划)学习笔记。本文是关于其中4.2节(策略迭代)。
(4.3) 策略迭代
基于上节(RL笔记:动态规划(1): 策略估计和策略提升)的策略提升,一旦从策略\pi出发找到了一个更好的策略;很显然,我们可以进一步基于
找到下一个更好的
。重复这一过程,就可以得到不断改进的策略,直到收敛到最优策略。这一过程称为策略迭代(Policy Iteration),如下图所示:
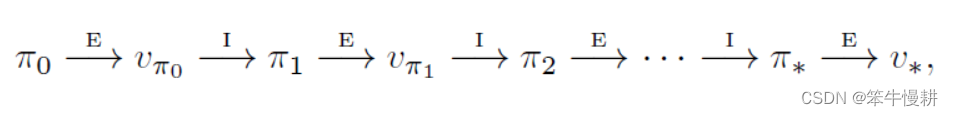
其中,“E”表示Evaluation,即上上节所述的策略评估;“I”表示Improvement,即上节所述的策略提升。由于每一步都必然可以得到一个更好的策略(除非已经到达最优策略,如上节所述),因此这一迭代过程最终必然收敛于最优策略(类似于数学分析中的单调有界序列必定收敛的命题)。
每一轮(each iteration)的策略评估是以是上一轮结束后得到的策略(policy)的值函数(value function)为初始值的。策略迭代的算法流程如下所示:

图1 基于状态值函数的策略迭代
Some points and tips:
- 这个两步策略是不是有点类似于机器学习中的EM(Expectation-Maximization算法)的套路?
- 第2步的策略评估中并没有像4.1节中的策略评估那样对动作进行求和:
。这是因为在这个迭代算法中第3步的策略提升采用的是贪婪算法,总是采取动作值函数最大的动作,所得到的策略是确定性策略(deterministic policy),每个状态与动作是一一对应的,所以由于
,可以进行简化。
- 第2步的策略评估中同时计算前后两轮迭代的各对应状态的值函数的变化量并得到变化量绝对值的最大值Δ,这个是用于收敛判断以及early-stop。如果满足条件
,即判定近似收敛并退出迭代过程
策略评估时根据当前策略选择动作,策略提升时根据基于策略
计算所得的值函数并基于
准则选择动作。除非当前策略
已经是最优策略,否则必然得到比当前策略
更好的策略。所以这一迭代过程最终必定“近似地”收敛于最优策略(近似是由于采用了early-stop控制)。
Example 4.2: Jack’s Car Rental
Jack负责管理一个全国性租车公司的两个站点。有顾客来租车时,如果有车可租则将车租出并收入10美元(是指每天10美元吗?还是说每借一次就是10美元不论天数?);如果无车可租则失去一笔生意。车归还后的次日车子可以重新出租。为了尽量确保两个站点都有车可租,Jack会在晚上在两个站点之间移动车辆,每辆车移动耗费2美元。每个站点每天来租车和来还车的人数均服从泊松分布:,
为数学期望。假定站点1的租车人数和还车人数的数学期望分别为3和4,站点2的租车人数和还车人数的数学期望分别为3和2。为了简化问题,进一步假定每个站点车辆不能超过20辆,超过这个数量的车被归还给租车公司。每个晚上可以在两个租车点移动的车最多5辆。考虑折扣系数
,并且作为一个continuing finite MDP问题处理:以每天作为一个time step; 状态代表每天结束时留在各站点的存车数。
状态用state = {num1: 站点1保有车数;num2: 站点2保有车数},这个保有车数是指每天最终(在两个站点挪动车之后)各站点保有车数。每天车的数量变化取决于以下因素:
- 当天借出车数:遵循泊松分布,以及当前站点存车状况
- 当天还入车数:遵循泊松分布,以及当前站点存车状况
- 当晚挪出或者挪入车数:是取决于agent(本问题中就是指Jack)基于policy所采取的行动
代码实现例可以参考:
https://github.com/ShangtongZhang/reinforcement-learning-an-introduction/chapter04/car_rental.py
其中expected_returns()函数实现的就是
这个例子中有一个明显的不太合理的地方,就是一辆车借出后的租金固定为10美元,与租用天数无关。这样可能是为了方便问题简化处理吧。如果修改为一辆车借出去每天租金10美元的话,情况会怎么样呢?
Exercise 4.4
前面所示的策略迭代算法有一个细微的bug。当存在两个或多个同样好的策略(所谓同样好是指啥?),它会导致在这些同样好的策略之间来回切换因而永远停不下来。请修改以上伪代码使得能够确保在有限次迭代后收敛和退出。
【ans】
在第3步中有一个收敛判决:if old_action 不等于 ...
如果在当前策略\pi中,在状态s时有多个动作同样好(equally good),此时不是一个值,而是包含多个元素的集合,以上判决处理将会导致问题。有两种解决方案:
其一:将以上收敛判决改为...
其二:追加tie-breaking rule between equally good actions,使得在存在多个同样好的动作时,策略总能产生唯一确定性的动作
Exercise 4.5
试给出与以上面向状态值函数的策略迭代算法类似的面向动作值函数的策略迭代算法。

图2 基于动作值函数的策略迭代
以上解答摘自LyWangPX/Reinforcement-Learning-2nd-Edition-by-Sutton-Exercise-Solutions(github.com)
变更点仅仅是第2步的策略评估中将基于“状态值函数的贝尔曼方程”的迭代更新改为基于“动作值函数的贝尔曼方程”的迭代更新。进一步由于第3步中是基于贪婪方法进行策略提升,所得的是确定性的策略,因此Q(s,a)的更新方程可以进一步简化(理由同上面关于基于状态值函数的策略迭代的解说)为(去掉对a’的求和):
第3步中的更新看似写法不同,其实没有本质变化。因为(之所以成立仍然是因为贪婪决策):
,前面的基于状态值函数的策略迭代流程中其实本质上也是基于动作值函数的贪婪决策。
Exercise 4.6
假定只能考虑软策略(soft policy),即在每个状态下选择各个动作的概率不得低于. 试修改上述的策略迭代算法以对应这种要求。
【Ans】
相比图1所示基于硬策略(hard policy, i.e, greedy policy)原始的策略迭代流程,需要做以下两点修改:
- 在策略评估(policy evaluation)中,由于软策略中每个状态下对应的动作不是唯一的,对状态值函数的估计需要对动作进行求和,即恢复为标准的状态值贝尔曼方程
- 在策略提升(policy improvement)中,要将更新后的策略修改为软策略,即:取导致动作价值最大的动作作为软策略的greedy-action,其余则作为epsilon-action。然后,同样是基于greedy-action进行收敛判决。
Exercise 4.7
请编写策略迭代程序解决Jack’s car rental problem,问题条件有一些变化:
- Jack的在站点1的一个员工住在站点2附近,每晚她可以免费驾驶移动一辆车到站点2。其余的车的移动仍然是每辆2美元
- 每个站点的停车位置有限,晚上存车超过10辆车(在两个站点间车辆移动后)需要额外支付4美元(不论超过多少辆)停车费
在真实问题中这类非线性条件以及任意转移函数(arbitrary dynamics)很常见,通常使用动态规划以外的优化方法很难求解。建议首先复现Example4.2中的结果。
......coming......
强化学习笔记:强化学习笔记总目录
相关文章:
RL笔记:动态规划(2): 策略迭代
目录 0. 前言 (4.3) 策略迭代 Example 4.2: Jack’s Car Rental Exercise 4.4 Exercise 4.5 Exercise 4.6 Exercise 4.7 0. 前言 Sutton-book第4章(动态规划)学习笔记。本文是关于其中4.2节(策略迭代)。 (4.3) 策略迭代 基…...

2023软件测试金三银四常见的软件测试面试题-【测试理论篇】
三、测试理论 3.1 你们原来项目的测试流程是怎么样的? 我们的测试流程主要有三个阶段:需求了解分析、测试准备、测试执行。 1、需求了解分析阶段 我们的SE会把需求文档给我们自己先去了解一到两天这样,之后我们会有一个需求澄清会议, 我…...

蓝桥训练第二周
1 ,泛凯撒加密 内存限制:128 MB时间限制:1.000 S 题目描述 众所周知,在网络安全中分为明文和密文,凯撒加密是将一篇明文中所有的英文字母都向后移动三位(Z的下一位是A),比如a向后…...

详讲函数知识
目录 1. 函数是什么? 2. C语言中函数的分类: 2.1 库函数: 2.2 自定义函数 函数的基本组成: 3. 函数的参数 3.1 实际参数(实参): 3.2 形式参数(形参): …...
gin 框架初始教程文档
一 、gin 入门1. 安装gin :下载并安装 gin包:$ go get -u github.com/gin-gonic/gin2. 将 gin 引入到代码中:import "github.com/gin-gonic/gin"3.初始化项目go mod init gin4.完整代码package mainimport "github.com/gin-go…...

Maven的下载和安装【详细】
文章目录一、什么是Maven?二、Maven的安装与配置2.1下载Maven安装包2.2配置Maven环境变量2.3验证三、Idea配置Maven3.1配置 setting.xml文件3.2Idea配置Maven一、什么是Maven? Apache Maven是个项目管理和自动构建工具,基于项目对象模型&…...
[数据结构]:04-循环队列(数组)(C语言实现)
目录 前言 已完成内容 循环队列实现 01-开发环境 02-文件布局 03-代码 01-主函数 02-头文件 03-QueueCommon.cpp 04-QueueFunction.cpp 结语 前言 此专栏包含408考研数据结构全部内容,除其中使用到C引用外,全为C语言代码。使用C引用主要是为了…...
buu [GWCTF 2019]BabyRSA 1
题目描述: import hashlib import sympy from Crypto.Util.number import *flag GWHT{******} secret ******assert(len(flag) 38)half len(flag) / 2flag1 flag[:half] flag2 flag[half:]secret_num getPrime(1024) * bytes_to_long(secret)p sympy.nextp…...

codeforces 1669F
题意: alice和bob从数组两边的吃糖果, 数组的值就是糖果重量 要求alice和bob吃的糖果重量必须一样, 输出能吃几个糖果 这题最先想到的是前后缀相加 模拟一个前缀和 和 后缀和 在n/2的位置向前找前缀和 在n/2的位置向后找后缀和 找到第一个前缀和后缀和的下标输出就好 …...

高数考试必备知识点
三角函数与反三角函数的知识点 正弦函数 ysin x, 反正弦函数 yarcsin x • y sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x (π/2) kπ 为对称轴 • y arcsin x, x∈[–1,1]…...
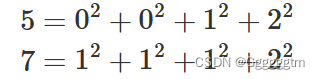
[蓝桥杯] 二分与前缀和习题练习
文章目录 一、二分查找习题练习 1、1 数的范围 1、1、1 题目描述 1、1、2 题解关键思路与解答 1、2 机器人跳跃问题 1、2、1 题目描述 1、2、2 题解关键思路与解答 1、3 四平方和 1、3、1 题目描述 1、3、2 题解关键思路与解答 二、前缀和习题练习 2、1 前缀和 2、1、1 题目描述…...
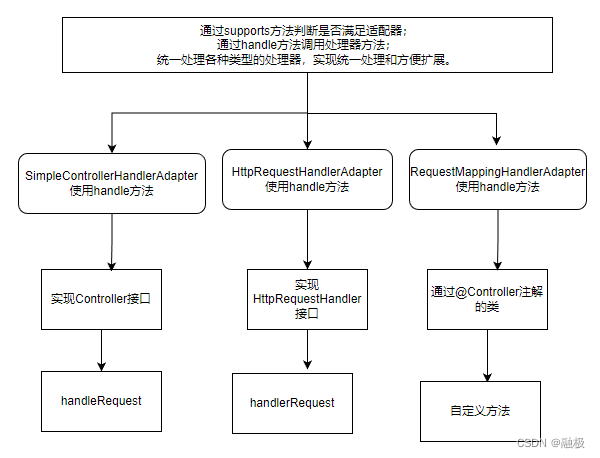
SpringMvc中HandlerAdapter组件的作用
概述 我们在使用springMVC时,都知道其中不仅包含handlerMapping组件还包含handlerAdapter组件,为什么呢? springMVC请求流程图 HandlerAdapter组件使用了适配器模式 适配器模式的本质是接口转换和代码复用,这里使用适配器模式的…...
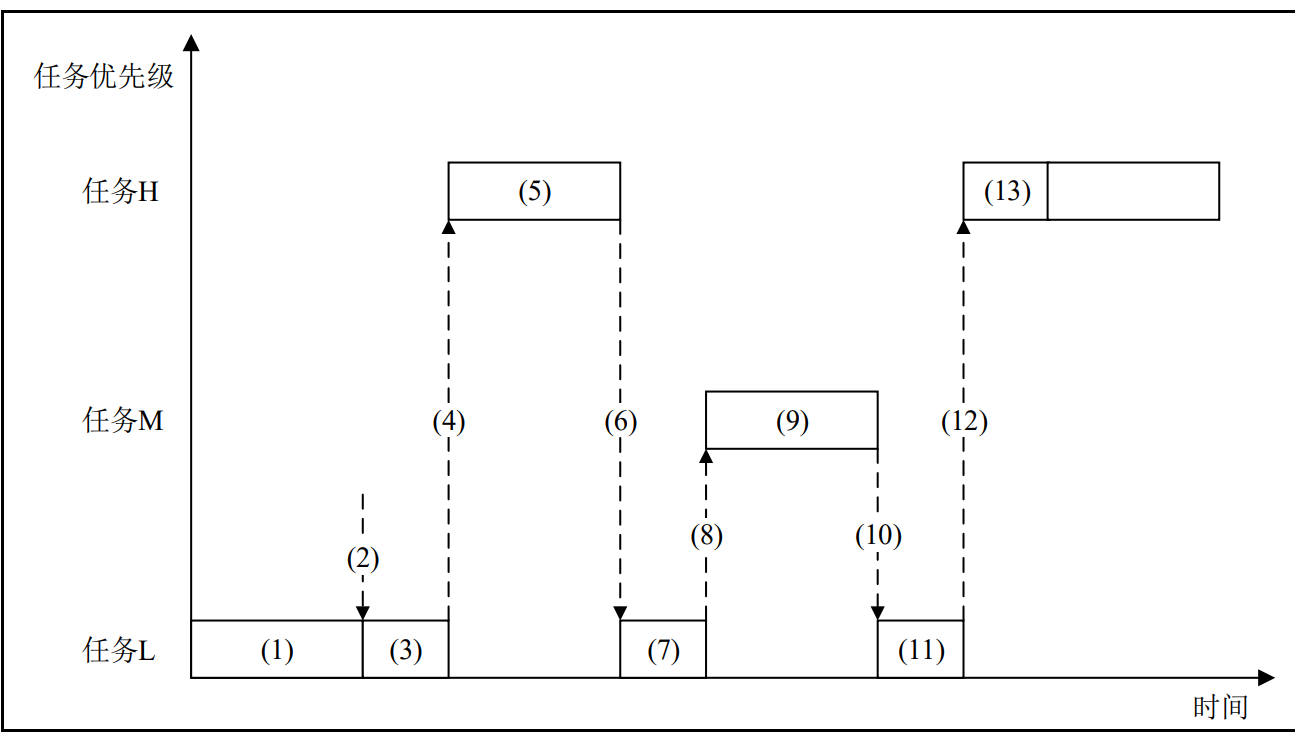
FreeRTOS优先级翻转
优先级翻转优先级翻转:高优先级的任务反而慢执行,低优先级的任务反而优先执行优先级翻转在抢占式内核中是非常常见的,但是在实时操作系统中是不允许出现优先级翻转的,因为优先级翻转会破坏任务的预期顺序,可能会导致未…...

服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】
我是用的xshell连接的云服务器,今天想在服务器上面部署一个前后端分离【springbootvue】项目,打开我的云服务器才发现,过期了,然后又买了一个,里面环境啥都没有,正好出一期教程,方便大家也方便自…...

golang项目----家庭收支记账软件
家庭收支记账软件实现基本功能(先使用面向过程,后面改成面向对象)项目代码实现改进面向过程源码面向对象源码utils包中main包中实现基本功能(先使用面向过程,后面改成面向对象) 编写文件TestMyAccount.go完成基本功能 功能一:先完成可以显示…...

中国LNG市场投资机会研究
中国LNG市场投资机会研究中国LNG市场是一个具有巨大潜力和发展机遇的市场,尤其是在政府大力推动清洁能源发展的背景下,LNG市场投资机会正在不断扩大。首先,政府大力支持LNG市场的发展。政府实施的“十三五”规划将LNG作为清洁能源的重要来源&…...
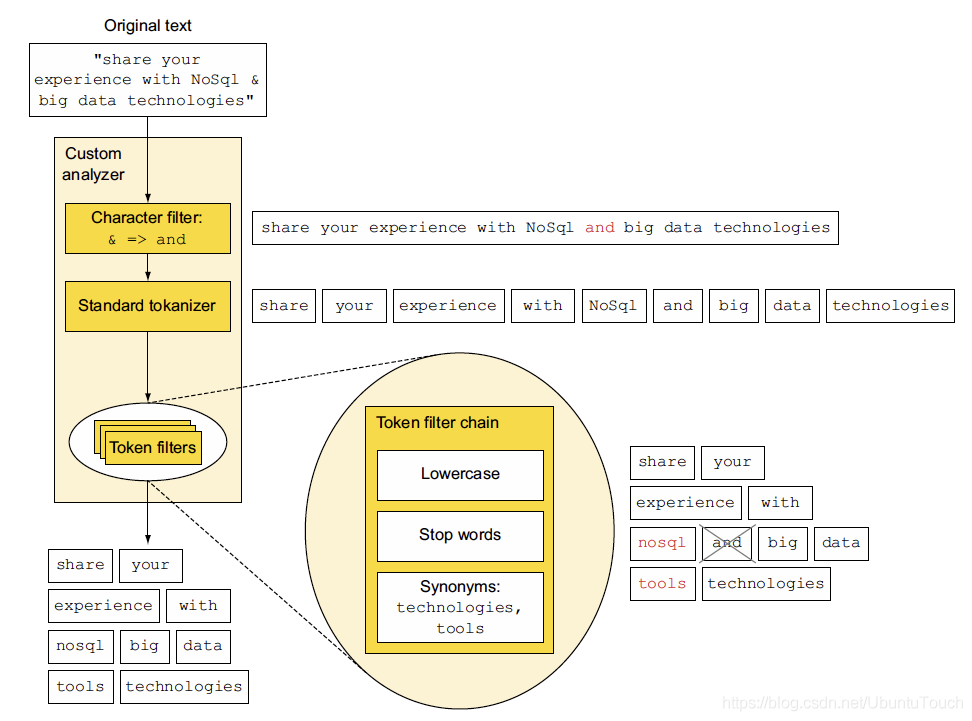
Elasticsearch:索引数据是如何完成的
在我在之前的文章 “Elasticsearch:彻底理解 Elasticsearch 数据操作” 文章中,我详细地描述了如何索引数据到 Elasticsearch 中。在今天的文章中,我想更进一步来描述这个流程。 Elasticsearch 是一个非常强大和灵活的分布式数据系统&#x…...

处理器管理
处理器状态处理器管理是操作系统中重要组成部分,负责管理、调度和分配计算机系统的重要资源——处理器,并控制程序执行由于处理器管理是操作系统最核心的部分,无论是应用程序还是系统程序,最终都要在处理器上执行以实现其功能&…...
第五)
跟着我从零开始入门FPGA(一周入门系列)第五
5、同步和异步设计 前面已有铺垫,同步就是与时钟同步。 同步就是走正步,一二一,该迈哪个脚就迈那个脚,跑的快的要等着跑的慢的。 异步就是搞赛跑,各显神通,尽最大力量去跑,谁跑得快,…...

【第42天】Arrays.sort 与 Collections.sort 应用 | 整形数组与集合的排序
本文已收录于专栏🌸《Java入门一百练》🌸学习指引序、专栏前言一.sort函数二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析三、推荐专栏序、专栏前言 本专栏开启,目的…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
