USACO12OPEN Balanced Cow Subsets G(meet in the middle)
洛谷P3067 [USACO12OPEN] Balanced Cow Subsets G
题目大意
我们定义一个奶牛集合 S S S是平衡的,当且仅当满足以下两个条件:
- S S S非空
- S S S可以被划分为两个集合 A , B A,B A,B,满足 A A A里的奶牛产量之和等于 B B B里的牛奶产量之和
现在给定大小为 n n n的奶牛集合 S S S,询问它有多少个子集是平衡的。
1 ≤ n ≤ 20 , 1 ≤ a i ≤ 1 0 8 1\leq n\leq 20,1\leq a_i\leq 10^8 1≤n≤20,1≤ai≤108
题解
前置知识:折半搜索(meet in the middle)
我们考虑枚举 S S S的子集 S ′ S' S′,在枚举子集 S ′ S' S′中的每个子集来判断 S ′ S' S′是否平衡。每个奶牛有三种情况:不在 S S S中,在 S S S中但不在 S ′ S' S′中,在 S S S中且在 S ′ S' S′中。如果枚举每种情况的话,时间时间复杂度是 O ( 3 n ) O(3^n) O(3n)的,我们考虑优化。
我们可以用折半搜索,将所有奶牛分为两个部分。
设前一部分中划分到集合 A A A的元素的值之和为 a a a,划分到集合 B B B的元素的值之和为 b b b。
设后一部分中划分到集合 A A A的元素的值之和为 c c c,划分到集合 B B B的元素的值之和为 d d d。
那么, a + c = b + d a+c=b+d a+c=b+d,移项的 a − b = c − d a-b=c-d a−b=c−d。
我们先处理出前一部分的 a − b a-b a−b,然后对于每一个 c − d c-d c−d,在前面处理出的 a − b a-b a−b中查找与 c − d c-d c−d相等的并判断这两部分构成的集合是否是平衡的,是的话就更新答案即可。
处理前一部分和后一部分的时间复杂度都为 O ( 3 n / 2 ) O(3^{n/2}) O(3n/2),合并的时间复杂度为 O ( n 3 n ) O(n3^n) O(n3n),所以总时间复杂度为 O ( n 3 n ) O(n3^n) O(n3n)。
code
#include<bits/stdc++.h>
using namespace std;
int n,cnt=0,ans=0,a[25],z[1<<20];
map<int,int>mp;
vector<int>v[1<<20];
void dfs1(int t,int sum,int now){if(t==n/2+1){if(!mp[sum]) mp[sum]=++cnt;v[mp[sum]].push_back(now);return;}dfs1(t+1,sum+a[t],now|(1<<t-1));dfs1(t+1,sum-a[t],now|(1<<t-1));dfs1(t+1,sum,now);
}
void dfs2(int t,int sum,int now){if(t==n+1){int tmp=mp[sum];if(tmp)for(int i=0;i<v[tmp].size();i++){z[v[tmp][i]|now]=1;}return;}dfs2(t+1,sum+a[t],now|(1<<t-1));dfs2(t+1,sum-a[t],now|(1<<t-1));dfs2(t+1,sum,now);
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}dfs1(1,0,0);dfs2(n/2+1,0,0);for(int i=1;i<1<<n;i++) ans+=z[i];printf("%d",ans);return 0;
}
相关文章:
)
USACO12OPEN Balanced Cow Subsets G(meet in the middle)
洛谷P3067 [USACO12OPEN] Balanced Cow Subsets G 题目大意 我们定义一个奶牛集合 S S S是平衡的,当且仅当满足以下两个条件: S S S非空 S S S可以被划分为两个集合 A , B A,B A,B,满足 A A A里的奶牛产量之和等于 B B B里的牛奶产量之和 …...

GIT常用操作记录
1、后悔药:强制回退到某个具体历史提交记录,并强制推送到远程仓库 强制回退到某个具体历史提交记录,即要删除它之后的所有提交,可以用 git reset 命令。 首先找到目标提交记录的ID,可以在github远程仓库的历史提交记…...

【ETL工具】Datax-ETL-SqlServerToHDFS
🦄 个人主页——🎐个人主页 🎐✨🍁 🪁🍁🪁🍁🪁🍁🪁🍁 感谢点赞和关注 ,每天进步一点点!加油!&…...
概述)
Kubernetes (K8S)概述
1、K8S 是什么? K8S 的全称为 Kubernetes (K12345678S),PS:“嘛,写全称也太累了吧,不如整个缩写”。 1.1 作用 用于自动部署、扩展和管理“容器化(containerized)应用程序”的开源系统。 可以…...
11月14号|Move生态Meetup相约浪漫土耳其
Move是基于Rust编程语言,由Mysten Labs联合创始人兼CTO Sam Blackshear在Meta的Libra项目中开发而来,旨在为开发者提供比现有区块链语言更通用的开发语言。Sam的目标是创建Web3的JavaScript,即一种跨平台语言,使开发人员能够在多个…...

mac vim没有颜色 问题
vim ~/.vimrc syntax on set nu! set autoindent...
Servlet核心API
目录 HttpServlet init destory service 实例:处理get、post、put、delete请求 1.通过postman得到请求 2.通过ajax得到请求 HttpServletRequest 常见方法 前端给后端传参 1.GET,query string 2.POST,form 3.POST,json HttpSeverletRespons…...

crs 维护模式 exclusive mode
How To Validate ASM Instances And Diskgroups On A RAC Cluster (When CRS Does Not Start). (Doc ID 1609127.1)编辑To Bottom [rootrac1 ~]# ps -ef|grep grid root 2477 1 1 20:47 ? 00:00:51 /opt/oracle.ahf/jre/bin/java -server -Xms32m -Xmx64…...
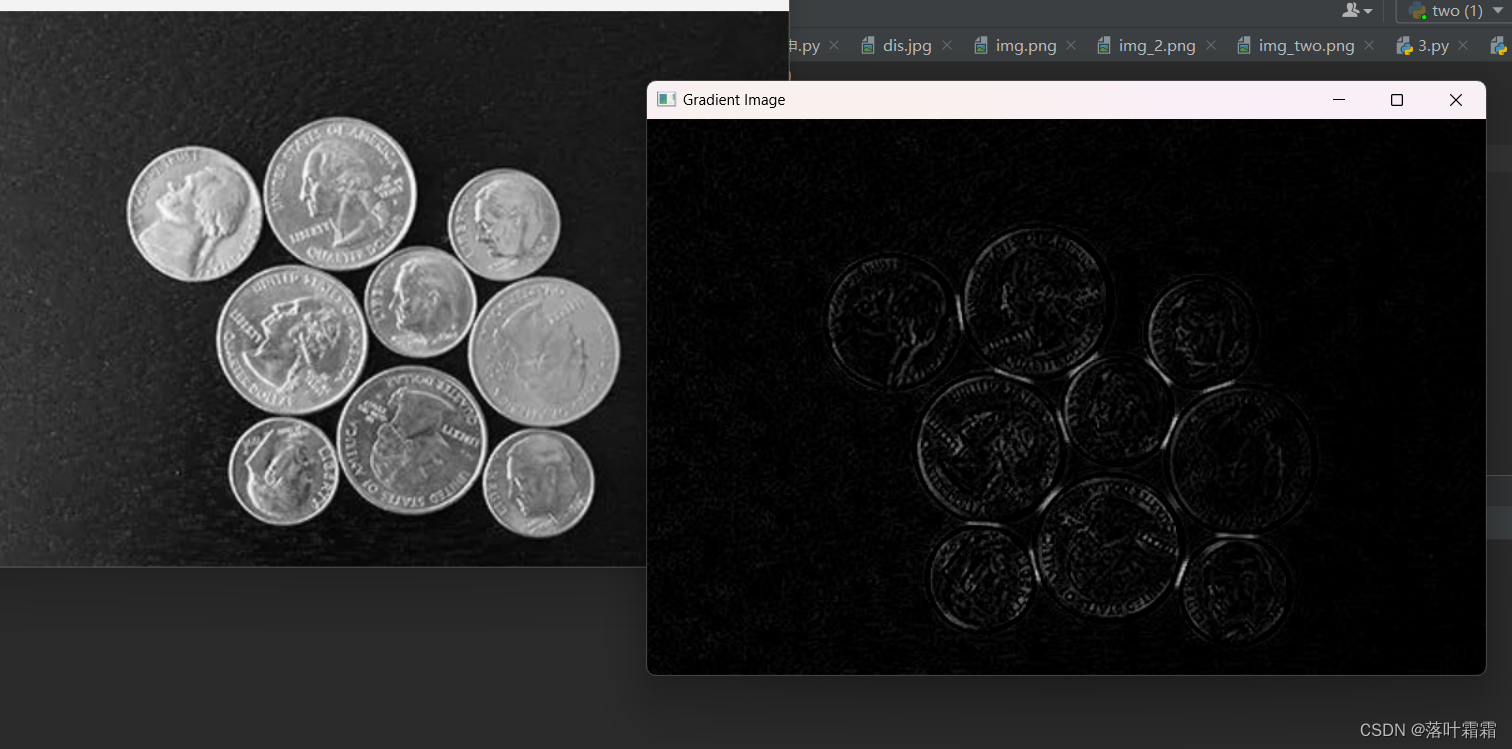
【OpenCV实现平滑图像形态学变化】
文章目录 概要目标腐蚀膨胀开运算结构元素(内核)小结 概要 形态学变化是一组简单的图像操作,主要用于处理二值图像,即只包含黑和白两种颜色的图像。这些操作通常需要两个输入,原始图像和一个内核(kernel&a…...

Ubuntu服务器中java -jar 后台运行Spring Boot项目
问:我在我的服务器中java -jar 运行springboot项目,但是我操作不了命令了,必须要终止掉才能执行后面的操作,怎么样才能让他后台运行呢?比如我的jar包名是tools-boot-0.0.1-SNAPSHOT.jar 使用nohup命令: 在…...

微服务parent工程和子工程pom文件配置注意
parent工程 重要配置: <!-- 父工程 --><packaging>pom</packaging><!-- 聚合 --><modules><module>../base</module><module>../gateway</module><module>../user-service</module><mod…...
STM32G030F6P6点灯闪烁
前言 (1)如果有嵌入式企业需要招聘湖南区域日常实习生,任何区域的暑假Linux驱动实习岗位,可C站直接私聊,或者邮件:zhangyixu02gmail.com,此消息至2025年1月1日前均有效 (2࿰…...

K8s开发人员也需要了解的相关知识
工作变动总结一下之前的笔记,整理一个速查的东西,方便之后查阅 K8s开发相关 1、k8s yml apiverison: Kubernetes (k8s) 的 API 版本表示资源定义在 API 服务器中的稳定性和支持程度。API 版本由一个字符串表示,如 v1 或 apps/v1,…...
创建并启动华为HarmonyOS本地与远程模拟器及远程真机
1.打开设备管理器 2.选择要添加的手机设备,然后点击安装 3.正在下载华为手机模拟器 4.下载完成 5.创建新模拟器 下载系统镜像 点击下一步,创建模拟器 创建成功 启动模拟器 华为模拟器启动成功 6.登陆华为账号并使用远程模拟器 7.使用远程真机...
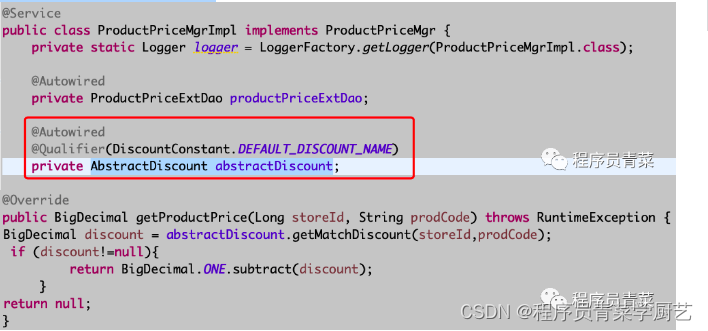
责任链模式应用案例
前几天系统商品折扣功能优化,同事采用了责任链模式重构了代码,现整理如下。 一、概念 责任链模式是为请求创建一个处理者对象的链条,所有处理者(除最末端)都含有下一个对象的引用从而形成一条处理链,该模…...

给你一个整数 num ,返回 num 中能整除 num 的数位的数目
给你一个整数 num ,返回 num 中能整除 num 的数位的数目。 如果满足 nums % val 0 ,则认为整数 val 可以整除 nums 。 示例 1: 输入:num 7 输出:1 解释:7 被自己整除,因此答案是 1 。 示例 2&…...
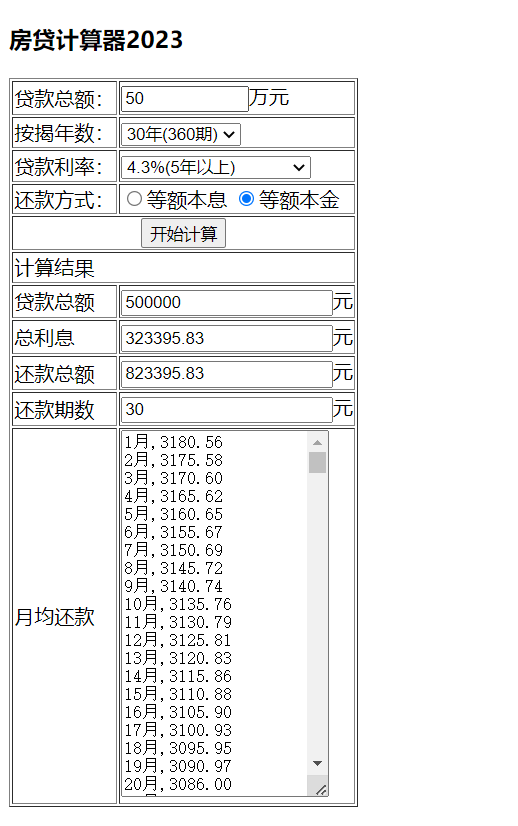
Java后端开发——房贷计算器(Ajax版、Json版、等额本息+等额本金)
MVC房贷计算器(Ajax版) 1.新建一个JavaWeb项目hslcalweb,设置tomcat10。 2.创建房贷计算器JavaBean:HslCalBean.java,增加以下的属性,并生成Getter/Setter方法。 private double total; //贷款额度pr…...

2023.10.28 关于 synchronized 原理
目录 synchronized 特性 synchronized 优化机制 锁升级(锁膨胀) 其他优化机制 锁消除 锁粗化 synchronized 特性 开始时是乐观锁,如果锁冲突频繁,就转为悲观锁开始是轻量级锁,如果锁被持有的时间较长,…...

力扣 27. 移除元素
目录 1.解题思路2.代码实现 1.解题思路 利用双指针思路,当让一个指针先走,指针指向的位置不等于val时,将此时该指针的值给另一个指针并且两个指针都加一,如果等于val,则让该指针加一继续走.最后另一个指针的下标就为排好的数组的…...
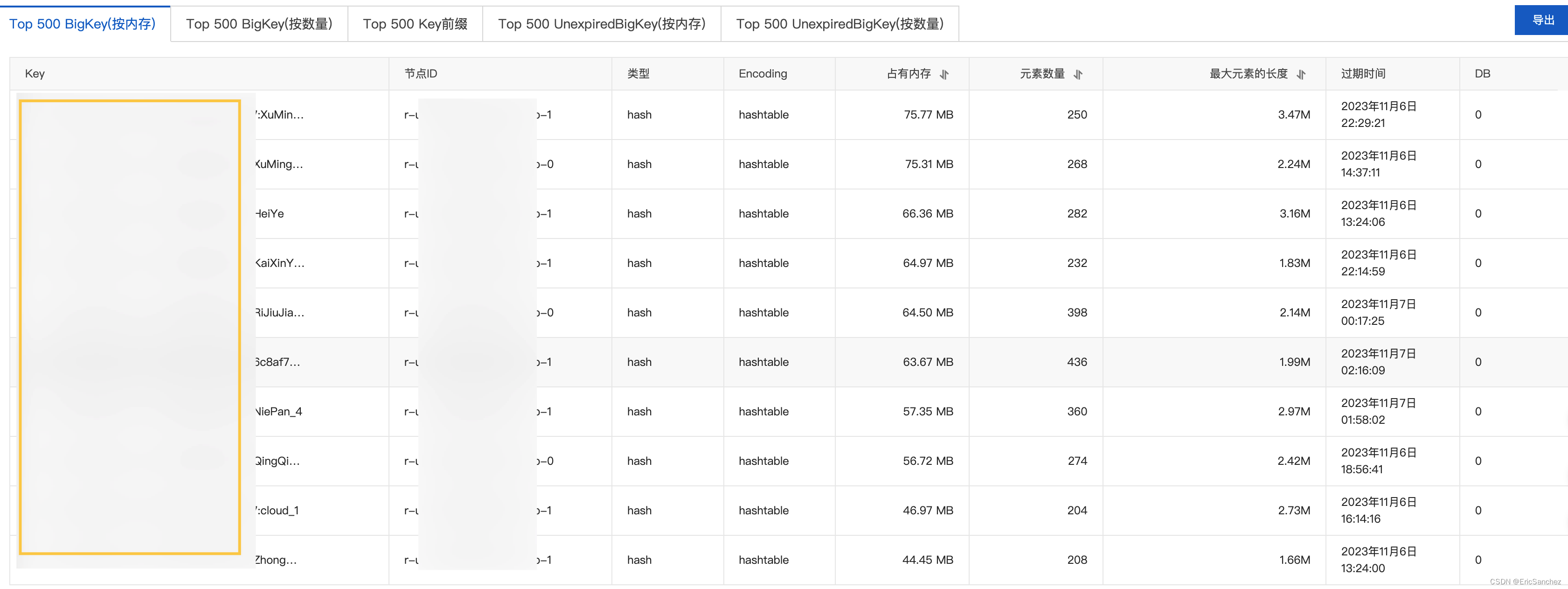
redis爆满导致数据丢失
记一则redis爆满导致数据丢失的一场事故 某功能上线后,发现出现问题,最后定位到了 redis. 由于存储的数据过多,导致阿里云4G大小的 redis 爆满,触发了回收策略。 于是临时扩容,运维同学当时未找到阿里云配置。 后面我用工具连接了…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
