【计算机视觉】对极几何

文章目录
- 一、极线约束(Epipolar Constraint)
- 二、相机标定过的情况
- 三、相机没有标定过的情况
- 四、八点算法(eight-point algorithm)
我的《计算机视觉》系列参考UC Berkeley的CS180课程,PPT可以在课程主页看到。
在上一篇文章3D视觉中我们介绍了在两个照相机像平面共面的情况下如何计算深度:深度与景物在图片中的位移成反比。这篇文章我们讨论更一般的情形,像平面不必共面,甚至不必平行。假设两个相机的内参(intrinsics)都是标定(calibrate)过的。
一、极线约束(Epipolar Constraint)
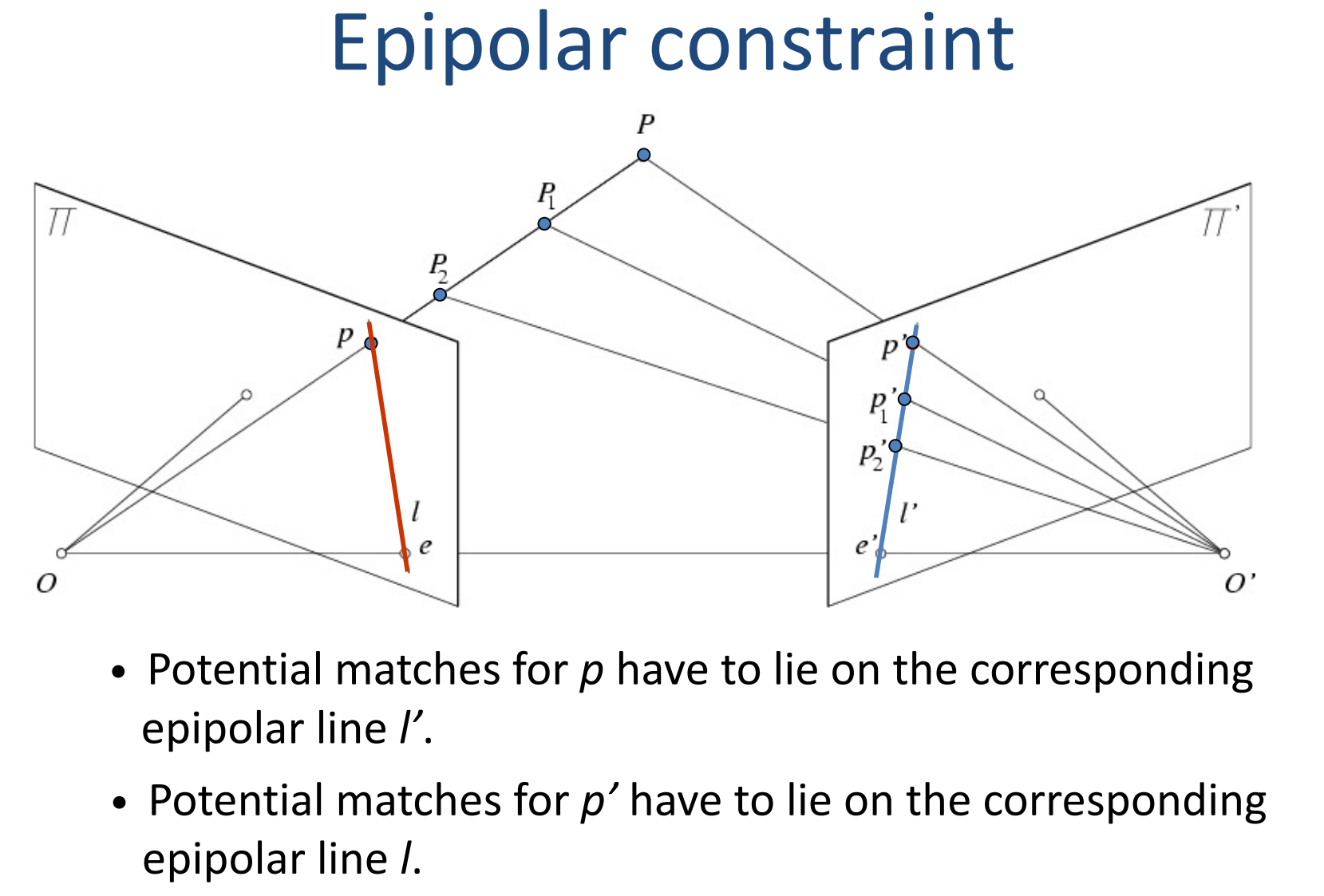
设两个相机的投影中心分别为 O O O和 O ′ O' O′(回想一下投影中心其实可以理解为所有光线都汇聚到的点),两个像平面分别为 Π \Pi Π和 Π ′ \Pi' Π′。设景物在 P P P点, O P OP OP与 Π \Pi Π交于点 p p p,这个 p p p就是景物在像平面 Π \Pi Π上的对应点。知道了 p p p在第一张照片上的坐标,就知道了景物所在的直线——图中的 O P OP OP。现在我们需要在第二张照片上找到景物对应的点。在哪儿找呢?上一篇文章我们讨论的情况中景物一定会出现在一条水平线上。在我们现在讨论的一般情况下,它还是出现在一条直线上吗?答案是肯定的。因为,任取 O P OP OP上的点 P 1 , P 2 , ⋯ P_1,P_2,\cdots P1,P2,⋯,令 O ′ P i O'P_i O′Pi与 Π ′ \Pi' Π′交于 p i ′ p_i' pi′, p i ′ p_i' pi′就是假设景物在 P i P_i Pi点时 其对应于第二张照片上的点。还是那个套路,我们知道 O P i OP_i OPi一定在 由 O P OP OP和 O O ′ OO' OO′确定的平面 O O ′ P OO'P OO′P上,那么 P i P_i Pi在第二张图片上的对应点 p i ′ p_i' pi′也一定在 平面 O O ′ P OO'P OO′P上;而 p ′ p' p′又在平面 Π ′ \Pi' Π′上,所以 p ′ p' p′一定在平面 Π ′ \Pi' Π′和平面 O O P ′ OOP' OOP′的交线上(图中的 l ′ l' l′)。所以,我们寻找 P P P在第二张图片上的对应点时只需要在直线 l ′ l' l′上寻找即可。直线 l l l和 l ′ l' l′称为极线(epipolar lines)。
但我们怎么知道极线 l ′ l' l′在哪里呢?两点确定一条直线,找到 l ′ l' l′上的两个点目前还有些困难,不过找到一个点是可以的。注意到, O O O点也在极线 O P OP OP上,而相机的内参是知道的,也就是说我们知道 O O O点的坐标(相对于 O ′ O' O′而言), O O ′ OO' OO′与 Π ′ \Pi' Π′的交点 e ′ e' e′一定在极线 l ′ l' l′上。 e ′ e' e′连同 O O ′ OO' OO′与 Π \Pi Π的交点 e e e被称为对极点(epipoles);其实就是一个相机看到另一个相机在图片中的位置,它不一定在图片上。当两个相机的像平面共面时,对极点 e e e和 e ′ e' e′就在无穷远处。 O O ′ OO' OO′称为摄影基线(baseline)。包含 O O ′ OO' OO′的所有平面称为极平面(epipolar plane),它绕着 O O ′ OO' OO′旋转;极平面和像平面的交点就是极线,它也绕着 O O ′ OO' OO′旋转。
二、相机标定过的情况
想要找到 l ′ l' l′上的另一个点其实是不可能的——没有另一个点可以找。但是,注意我们的相机是标定过的,我们知道两个相机之间的坐标变换。令点 p p p在第一个相机坐标系下的坐标为 x \boldsymbol{x} x,即 O P → = x \overrightarrow{OP}=\boldsymbol{x} OP=x,再令点 p ′ p' p′在第二个相机坐标系下的坐标为 x ′ \boldsymbol{x}' x′。现在我们在第二个相机坐标系(即 O ′ O' O′坐标系)下讨论问题。向量 x \boldsymbol{x} x就不能直接使用了,需要转换到 O ′ O' O′坐标系: x O = R x + t \boldsymbol{x}_O=R\boldsymbol{x}+\boldsymbol{t} xO=Rx+t,其中 R R R是旋转矩阵, t = O O ′ → \boldsymbol{t}=\overrightarrow{OO'} t=OO′是平移向量。我们还知道, x , x ′ , t \boldsymbol{x},\boldsymbol{x}',\boldsymbol{t} x,x′,t是共面的,即 x ′ ⋅ ( t × x O ) = 0 \boldsymbol{x}'\cdot(\boldsymbol{t}\times\boldsymbol{x}_O)=0 x′⋅(t×xO)=0其中 t × x \boldsymbol{t}\times\boldsymbol{x} t×x是极平面的法向量, x ′ \boldsymbol{x}' x′与其点积为 0 0 0说明与其垂直,进而说明 x ′ \boldsymbol{x}' x′在极平面上。化简: t × x O = t × ( R x + t ) = t × R x + x × t = t × R x + 0 = t × R x \boldsymbol{t}\times\boldsymbol{x}_O=\boldsymbol{t}\times (R\boldsymbol{x}+\boldsymbol{t})=\boldsymbol{t}\times R\boldsymbol{x}+\boldsymbol{x}\times \boldsymbol{t}=\boldsymbol{t}\times R\boldsymbol{x}+\boldsymbol{0}=\boldsymbol{t}\times R\boldsymbol{x} t×xO=t×(Rx+t)=t×Rx+x×t=t×Rx+0=t×Rx因此有 x ′ ⋅ ( t × R x ) = 0 \boldsymbol{x}'\cdot(\boldsymbol{t}\times R\boldsymbol{x})=0 x′⋅(t×Rx)=0叉乘可以转化成与一个反对称矩阵 [ t × ] [\boldsymbol{t}_\times] [t×]的乘法:
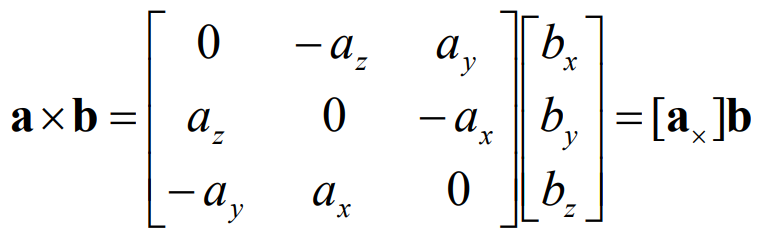
故等式化为 x ′ T [ t × ] R x = 0 \boldsymbol{x}'^T[\boldsymbol{t}_\times]R\boldsymbol{x}=0 x′T[t×]Rx=0。令 E = [ t × ] R E=[\boldsymbol{t}_\times]R E=[t×]R,则有 x ′ T E x = 0 \boldsymbol{x}'^TE\boldsymbol{x}=0 x′TEx=0这就是Longuet-Higgins方程。 E E E被称为本质矩阵(Essential Matrix)。
其实, E x E\boldsymbol{x} Ex就表示极线 l ′ l' l′。设 l ′ l' l′在像平面上的方程为 a x ′ + b y ′ + c = 0 ax'+by'+c=0 ax′+by′+c=0,即 [ a , b , c ] [ x ′ , y ′ , 1 ] T = 0 [a,b,c][x',y',1]^T=0 [a,b,c][x′,y′,1]T=0。注意像平面 Π ′ \Pi' Π′的法向量和 O ′ O' O′坐标系下的 z z z轴平行(即 Π ′ \Pi' Π′与 x ′ O y ′ x'Oy' x′Oy′面平行),所以 x ′ , y ′ x',y' x′,y′既是 O ′ O' O′坐标系下的横纵坐标,也是像平面坐标系下的横纵坐标。那么 a , b , c a,b,c a,b,c就可以用 E x E\boldsymbol{x} Ex来确定了。
最后, E E E是奇异矩阵,秩为 2 2 2,有五个自由度:3个平移,2个旋转(平面绕法线旋转等于没旋转,所以少一个旋转自由度)。
三、相机没有标定过的情况
设图像上的坐标为 ( u , v ) (u,v) (u,v),令 x ^ = [ u , v , 1 ] T \hat{\boldsymbol{x}}=[u,v,1]^T x^=[u,v,1]T。令 K K K和 K ′ K' K′分别是连哥哥相机的 3 × 3 3\times 3 3×3版本的内参矩阵(intrinsic matrix),则 x = K − 1 x ^ \boldsymbol{x}=K^{-1}\hat{\boldsymbol{x}} x=K−1x^, x ′ = K ′ − 1 x ^ ′ \boldsymbol{x}'=K'^{-1}\hat{\boldsymbol{x}}' x′=K′−1x^′,代入 x ′ T E x = 0 \boldsymbol{x}'^TE\boldsymbol{x}=0 x′TEx=0得 x ^ ′ T ( K ′ − 1 ) T E K − 1 ⏟ F x ^ = 0 \hat{\boldsymbol{x}}'^T\underset{F}{\underbrace{{(K'^{-1})}^TEK^{-1}}}\hat{\boldsymbol{x}}=0 x^′TF (K′−1)TEK−1x^=0其中 F = ( K ′ − 1 ) T E K − 1 F={(K'^{-1})}^TEK^{-1} F=(K′−1)TEK−1称为基础矩阵(Fundamental Matrix)。它也是秩为2的矩阵,有7个自由度:秩为2相当于多一个方程,损失一个自由度;把 F F F放大若干倍等式不变,再损失一个自由度。
四、八点算法(eight-point algorithm)
如何求得基础矩阵 F F F呢?还是老套路,线性回归。给定两张图片上的8个点对,代入方程 x ^ ′ T F x ^ = 0 \hat{\boldsymbol{x}}'^T F\hat{\boldsymbol{x}}=0 x^′TFx^=0用最小二乘法求得最优的 F F F即可。
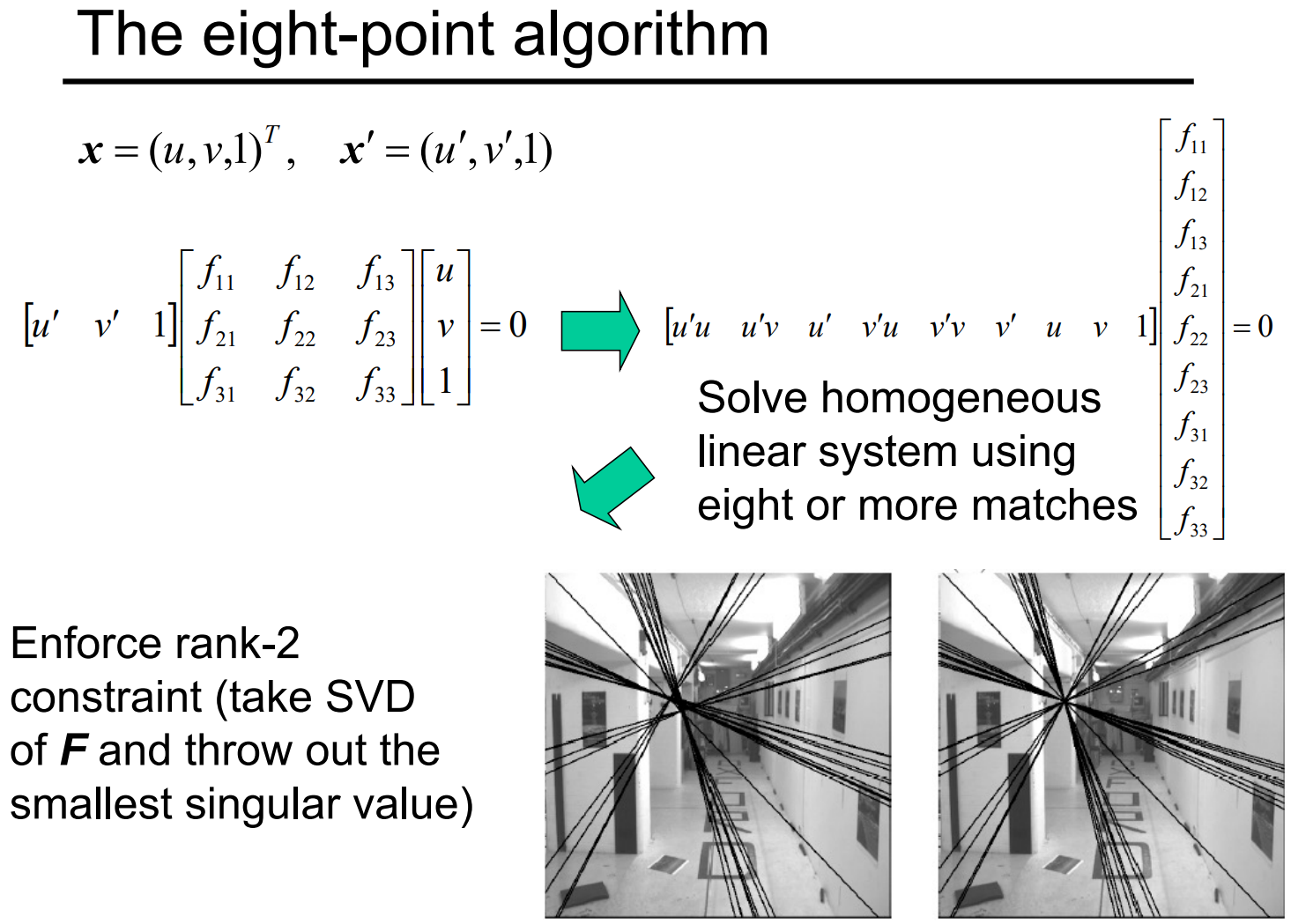
用 8 8 8个点是利用到了秩为 2 2 2的约束,少了一个自由度;另外一个缺失的自由度没必要利用,因为没必要手动确定 F F F的缩放大小。实践中应该用多于 8 8 8个点。
最后,如果我们标定了相机,那么就可以从 F F F求得 E E E;而 E E E又可以进行奇异值分解最终还原 R R R和 t \boldsymbol{t} t。过程比较复杂,可以参考https://inst.eecs.berkeley.edu/~ee290t/fa19/lectures/lecture10-3-decomposing-F-matrix-into-Rotation-and-Translation.pdf。
相关文章:

【计算机视觉】对极几何
文章目录 一、极线约束(Epipolar Constraint)二、相机标定过的情况三、相机没有标定过的情况四、八点算法(eight-point algorithm) 我的《计算机视觉》系列参考UC Berkeley的CS180课程,PPT可以在课程主页看到。 在上一…...
强大易于编辑的流程图组织图绘制工具draw.io Mac苹果中文版
draw.io可以绘制多种类型的图表,包括但不限于流程图、组织结构图、网络图、UML图、电气工程图等。draw.io提供了丰富的图形元素和编辑功能,使用户能够轻松地创建和编辑各种复杂的图表。同时,该软件还支持多种导出格式,方便用户在不…...
c# .net6 在线条码打印基于
条码打印基于:BarTender、ORM EF架构 UI展示: 主页代码: using NPOI.OpenXmlFormats.Spreadsheet; using ServerSide.Models; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawi…...

Hive SQL的编译过程
1.MapReduce实现基本SQL操作的原理 详细讲解SQL编译为MapReduce之前,我们先来看看MapReduce框架实现SQL基本操作的原理 1.1 Join的实现原理 select u.name, o.orderid from order o join user u on o.uid = u.uid; 在map的输出value中为不同表的数据打上tag标记,在reduce阶段…...
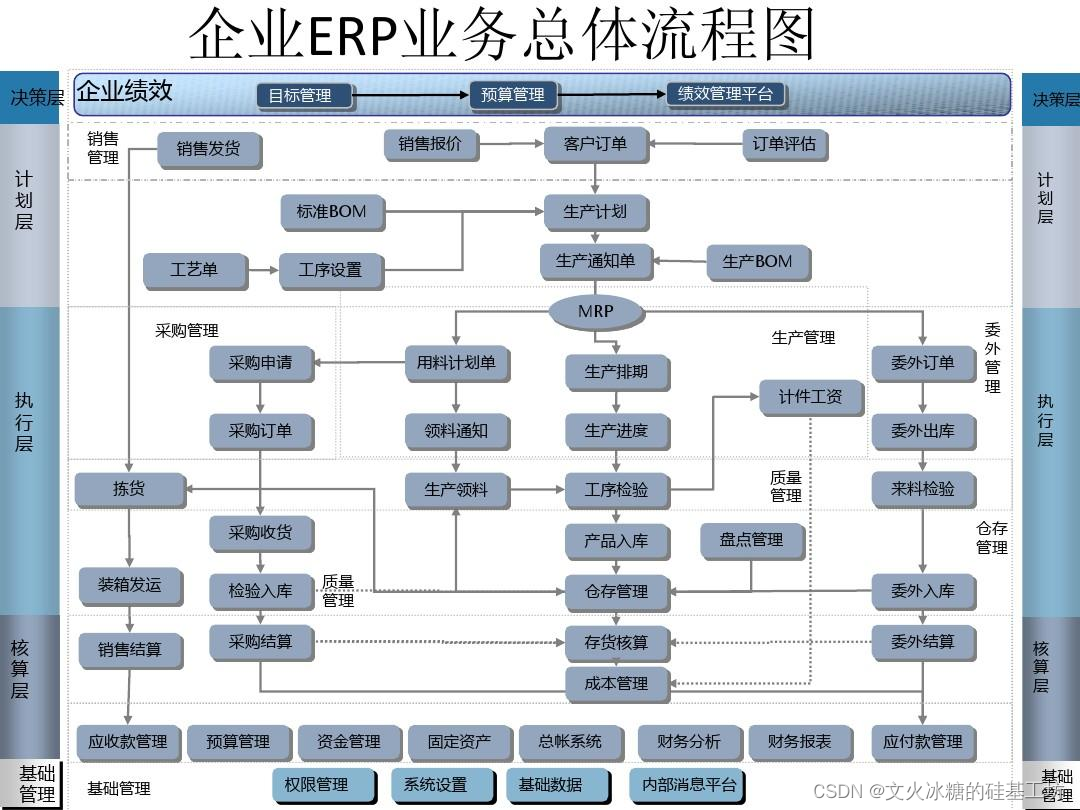
[架构之路-245/创业之路-76]:目标系统 - 纵向分层 - 企业信息化的呈现形态:常见企业信息化软件系统 - 企业资源管理计划ERP
目录 前言: 一、企业信息化的结果:常见企业信息化软件 1.1 企业资源管理计划 1.1.1 什么是ERP:企业最常用的信息管理系统 1.1.2 ERP的演进过程 1.1.3 EPR模块 1.1.4 EPR五个层级 1.1.5 企业EPR业务总体流程图 1.1.6 什么类型的企业需…...

数据库简史:多主数据库架构的由来和华为参天引擎的机遇
注:本文发表后,收到了很多后台反馈,其中关于大型机的早期成就不容省略。微调重发本文,纯属个人观点,错谬之处,仍然期待指正。 2023年10月13日,在北京举办的“2023金融业数据库技术大会"上&…...
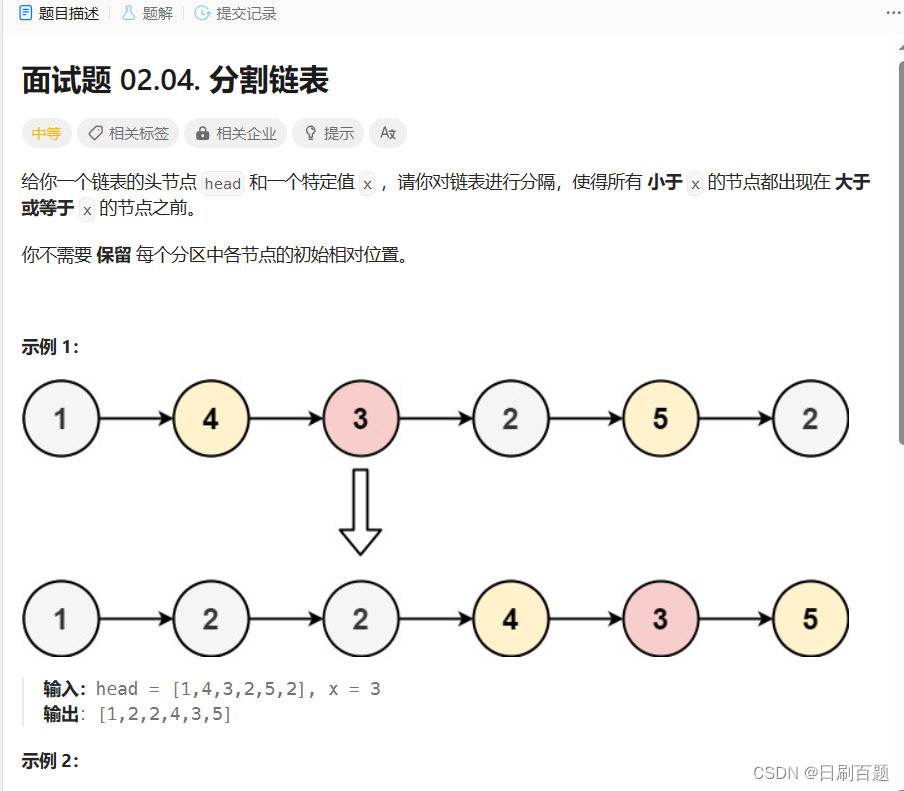
C语言每日一练(二)
单链表经典算法专题 一、 单链表相关经典算法OJ题1:移除链表元素 解法一:在原链表中删除Node.nextnext的节点 typedef struct ListNode ListNode; struct ListNode* removeElements( ListNode* head, int val) {ListNode* pcur head;ListNode* pre h…...
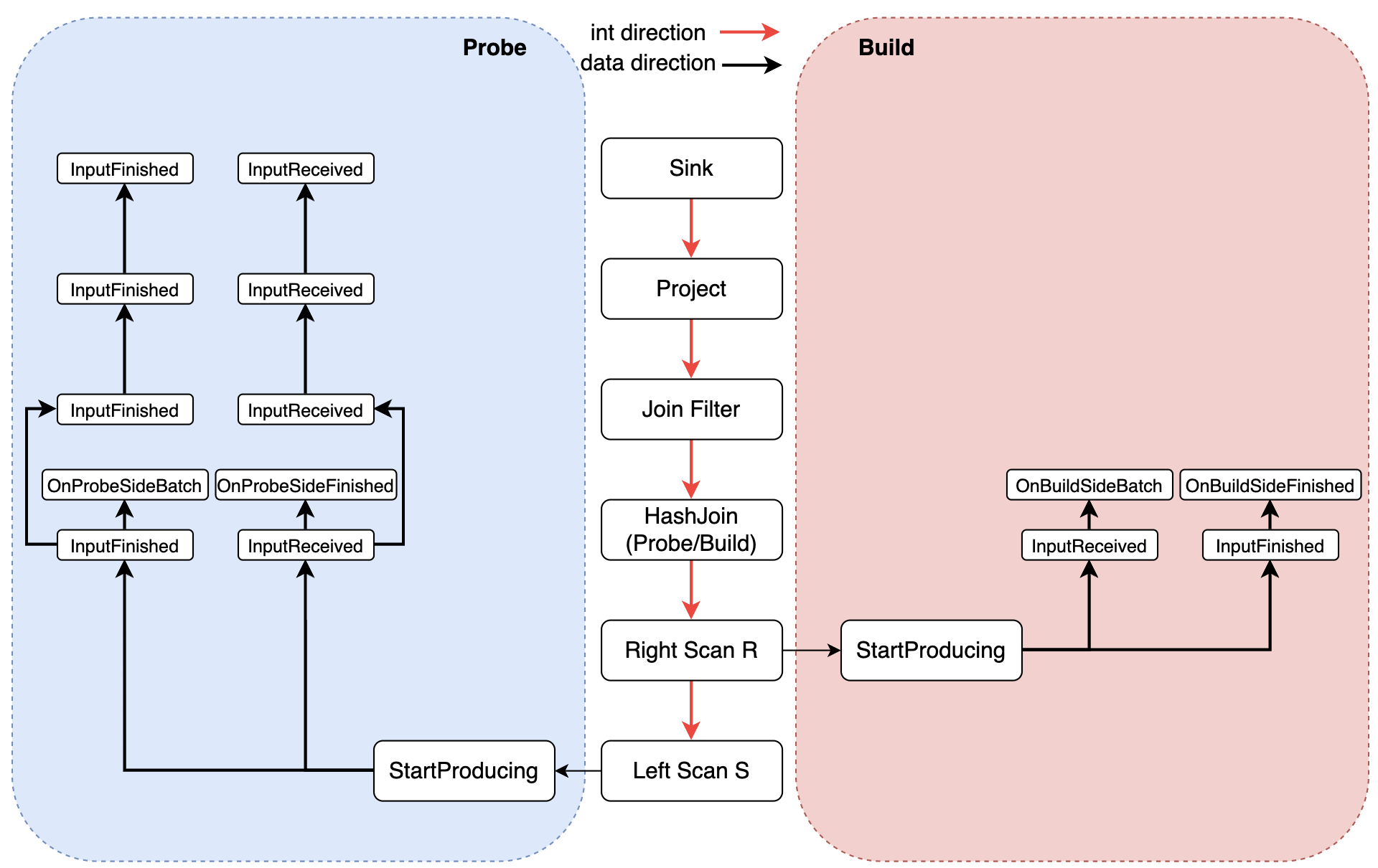
HashJoin 在 Apache Arrow 和PostgreSQL 中的实现
文章目录 背景PostgreSQL HashJoin实现PG 执行器架构HashJoin 基本流程HashJoin 实现细节Join 类型HashJoin 的划分阶段HashJoin 的分批处理阶段JOIN 类型的状态机转换HashJoin 的投影和过滤 Arrow Acero HashJoin实现Acero 基本框架HashJoin 基本流程 总结 背景 近两个月转到…...
FL Studio21.2.0.3421最新汉化破解版中文解锁下载完整版本
音乐在人们心中的地位日益增高,近几年音乐选秀的节目更是层出不穷,喜爱音乐,创作音乐的朋友们也是越来越多,音乐的类型有很多,好比古典,流行,摇滚等等。对新手友好程度基本上在首位,…...

docker在java项目中打成tar包
docker在java项目中打成tar包 1、首先安装一个docker desktop 2、mvn install项目后,建立一个自己的dockerfile 这里我以我的代码举例,from 镜像,这里你也能打包好一个镜像的基础上,from打好的镜像,这里我们用openj…...

No175.精选前端面试题,享受每天的挑战和学习
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...

【网安AIGC专题10.19】论文6:Java漏洞自动修复+数据集 VJBench+大语言模型、APR技术+代码转换方法+LLM和DL-APR模型的挑战与机会
How Effective Are Neural Networks for Fixing Security Vulnerabilities 写在最前面摘要贡献发现 介绍背景:漏洞修复需求和Java漏洞修复方向动机方法贡献 数据集先前的数据集和Java漏洞Benchmark数据集扩展要求数据处理工作最终数据集 VJBenchVJBench 与 Vul4J 的…...

解决国外镜像无法访问导致的R包无法安装问题
我自己的方法: install.packages("vcd", repos "https://mirrors.tuna.tsinghua.edu.cn/CRAN/") R包安装镜像设置的三种方法:R包安装镜像设置的三种方法 - 简书 更新了Rstudio后,出现 unable to access index for rep…...
【2021集创赛】Robei杯一等奖:基于Robei EDA工具的隔离病房看护机器人设计
本作品参与极术社区组织的有奖征集|秀出你的集创赛作品风采,免费电子产品等你拿~活动。 团队介绍 参赛单位:重庆交通大学 队伍名称:一丘之貉 指导老师:毕波 李艾星 参赛队员:郁航 张坤 秦衡 总决赛奖项:Robei杯一等奖…...

Python之函数-传实参的两种方式
Python之函数-传实参的两种方式 函数参数 函数在定义是要定义好形式参数,调用时也提供足够的实际参数,一般来说,形参和实参个数要一致(可变参数除外)。实参传参方式 1、位置传参 定义时def f(x, y, z), 调用使用 f(1, 3, 5)&am…...

Hive客户端和Beeline命令行的基本使用
本专栏案例数据集链接: https://download.csdn.net/download/shangjg03/88478038 1.Hive CLI 1.1 命令帮助Help 使用 `hive -H` 或者 `hive --help` 命令可以查看所有命令的帮助,显示如下: usage: hive-d,--define <key=value> Variable subsitution to ap…...

Ubuntu 22.04自动登录进入桌面
1.编辑gdm3配置文件 sudo vim /etc/gdm3/custom.conf 2.修改内容为 AutomaticLoginEnableTrue AutomaticLoginusername 3.查看和重启服务 # 查看服务状态 systemctl --user status gnome-remote-desktop.service # 重启服务 systemctl --user restart gnome-remote-deskt…...

C#__简单了解XML文档
/* XML(可扩展标记语言):用于传输和存储数据 XML文档:树结构;包含根元素 XML元素:从开始标签到结束标签的部分 XML语法规则: 1、所有XML元素都必须有结束标签 …...

云游数智农业世界,体验北斗时空智能
今日,2023年中国国际农业机械展览会在武汉正式拉开帷幕,众多与会者云集,各类农机产品纷呈,盛况空前。 千寻位置作为国家北斗地基增强系统的建设与运营方,在中国国际农业机械展览会上亮相,以「北斗时空智能 …...
C# 递归算法使用简介_常用整理
一、递归简介 递归算法是一种直接或者间接调用自身函数或者方法的算法。 递归算法的实质是把问题分解成规模缩小的同类问题的子问题,然后递归调用方法来表示问题的解。递归算法对解决一大类问题很有效,它可以使算法简洁和易于理解。 递归本质是循环&a…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
