条件期望4
条件期望例题----快排算法的分析
快速排序算法的递归定义如下:
有n个数(n≥2n\geq 2n≥2), 一开始随机选取一个数xix_ixi, 并将xix_ixi和其他n-1个数进行比较, 记SiS_iSi为比xix_ixi小的元素构成的集合, Siˉ\bar{S_i}Siˉ为比xix_ixi大的元素构成的集合, 然后分别对SiS_iSi和Siˉ\bar{S_i}Siˉ进行排序.
如果集合中元素个数等于2, 则简单比较即可, 如果大于2, 则重复上述过程.
我们选取整个排序过程中的比较次数的期望作为算法效率分析的指标. 记MnM_nMn为在n个不同元素的集合中, 实行快速排序算法所需要的比较次数的均值, 易知M0=M1=0,M2=0.5M_0 = M_1 = 0, M_2 = 0.5M0=M1=0,M2=0.5.
易知
Mn=∑j=1nE[比较次数∣初始随机取的元素为集合中的第j个值]1nM_n = \sum_{j=1}^nE[比较次数|初始随机取的元素为集合中的第j个值]\frac{1}{n} Mn=j=1∑nE[比较次数∣初始随机取的元素为集合中的第j个值]n1
如果初始选的值是所有元素中第jjj小的, 则对应的SSS集合就有j−1j-1j−1个元素, Sˉ\bar{S}Sˉ就有n-j个元素, 因为第一次选取之后一定会比较n−1n-1n−1次, 所以可得
Mn=∑j=1n(n−1+Mj−1+Mn−j)1n=n−1+1n∑k=1n−1Mk+1n∑m=n−11Mm=n−1+2n∑k=1n−1Mk\begin{split} M_n &= \sum_{j=1}^n(n-1 + M_{j-1} + M_{n-j})\frac{1}{n} \\ &=n-1 + \frac{1}{n}\sum_{k=1}^{n-1}M_k + \frac{1}{n}\sum_{m=n-1}^{1}M_m \\ &=n-1 + \frac{2}{n}\sum_{k=1}^{n-1}M_k \end{split} Mn=j=1∑n(n−1+Mj−1+Mn−j)n1=n−1+n1k=1∑n−1Mk+n1m=n−1∑1Mm=n−1+n2k=1∑n−1Mk
所以
nMn=n(n−1)+2∑k=1n−1MknM_n = n(n-1) + 2\sum_{k=1}^{n-1}M_k nMn=n(n−1)+2k=1∑n−1Mk
易知
(n+1)Mn+1=n(n+1)+2∑k=1nMk(n+1)M_{n+1} = n(n+1) + 2\sum_{k=1}^{n}M_k (n+1)Mn+1=n(n+1)+2k=1∑nMk
所以
(n+1)Mn+1−nMn=n(n−1)=2n+2Mn(n+1)M_{n+1} - nM_n = n(n-1) = 2n+2M_n (n+1)Mn+1−nMn=n(n−1)=2n+2Mn
即
(n+1)Mn+1=2n+(n+2)Mn(n+1)M_{n+1} = 2n+(n+2)M_n (n+1)Mn+1=2n+(n+2)Mn
所以
Mn+1=2nn+1+n+2n+1MnM_{n+1} = \frac{2n}{n+1} + \frac{n+2}{n+1}M_n Mn+1=n+12n+n+1n+2Mn
两边同除以(n+2)(n+2)(n+2), 有
Mn+1n+2=2n(n+1)(n+2)+Mnn+1\frac{M_{n+1}}{n+2} = \frac{2n}{(n+1)(n+2)} + \frac{M_n}{n+1} n+2Mn+1=(n+1)(n+2)2n+n+1Mn
迭代这个过程, 有
Mn+1n+2=2n(n+1)(n+2)+(2(n−1)n(n+1)+Mn−1n)=⋯=2∑k=0n−1n−k(n+1−k)(n+2−k)(M1=0)\begin{split} \frac{M_{n+1}}{n+2} &= \frac{2n}{(n+1)(n+2)} + \left(\frac{2(n-1)}{n(n+1)} + \frac{M_{n-1}}{n} \right) \\ &=\cdots \\ &=2\sum_{k=0}^{n-1}\frac{n-k}{(n+1-k)(n+2-k)} \\ &(M_1 = 0) \end{split} n+2Mn+1=(n+1)(n+2)2n+(n(n+1)2(n−1)+nMn−1)=⋯=2k=0∑n−1(n+1−k)(n+2−k)n−k(M1=0)
所以
Mn+1=2(n+2)∑i=1ni(i+1)(i+2)(i=n−k)=2(n+2)[∑i=1n2i+2−∑i=1n1i+1]≈2(n+2)[∫3n+22xdx−∫2n+11xdx](步长为1的数值积分)≈2(n+2)ln(n+2)\begin{split} M_{n+1} &= 2(n+2)\sum_{i=1}^{n}\frac{i}{(i+1)(i+2)} \\ &(i = n-k) \\ &=2(n+2)\left[\sum_{i=1}^{n}\frac{2}{i+2} - \sum_{i=1}^{n}\frac{1}{i+1} \right] \\ &\approx 2(n+2)\left[ \int_3^{n+2}\frac{2}{x}dx - \int_2^{n+1}\frac{1}{x}dx\right] \\ &(步长为1的数值积分) \\ &\approx 2(n+2)ln(n+2) \end{split} Mn+1=2(n+2)i=1∑n(i+1)(i+2)i(i=n−k)=2(n+2)[i=1∑ni+22−i=1∑ni+11]≈2(n+2)[∫3n+2x2dx−∫2n+1x1dx](步长为1的数值积分)≈2(n+2)ln(n+2)
相关文章:

条件期望4
条件期望例题----快排算法的分析 快速排序算法的递归定义如下: 有n个数(n≥2n\geq 2n≥2), 一开始随机选取一个数xix_ixi, 并将xix_ixi和其他n-1个数进行比较, 记SiS_iSi为比xix_ixi小的元素构成的集合, Siˉ\bar{S_i}Siˉ为比xix_ixi大的元素构成的集合, 然后分…...

网络协议分析(2)判断两个ip数据包是不是同一个数据包分片
一个节点收到两个IP包的首部如下:(1)45 00 05 dc 18 56 20 00 40 01 bb 12 c0 a8 00 01 c0 a8 00 67(2)45 00 00 15 18 56 00 b9 49 01 e0 20 c0 a8 00 01 c0 a8 00 67分析并判断这两个IP包是不是同一个数据报的分片&a…...

6.2 负反馈放大电路的四种基本组态
通常,引入交流负反馈的放大电路称为负反馈放大电路。 一、负反馈放大电路分析要点 如图6.2.1(a)所示电路中引入了交流负反馈,输出电压 uOu_OuO 的全部作为反馈电压作用于集成运放的反向输入端。在输入电压 uIu_IuI 不变的情况下,若由于…...

MySQL进阶之锁
锁是计算机中协调多个进程或线程并发访问资源的一种机制。在数据库中,除了传统的计算资源竞争之外,数据也是一种提供给许多用户共享的资源,如何保证数据并发访问的一致性和有效性是数据库必须解决堆的一个问题,锁冲突也是影响数据…...

【Mac 教程系列】如何在 Mac 上破解带有密码的 ZIP 压缩文件 ?
如何使用 fcrackzip 在 Mac 上破解带有密码的 ZIP 压缩文件? 用 markdown 格式输出答案。 在 Mac 上破解带有密码的 ZIP 压缩文件 使用解压缩软件,如The Unarchiver,将文件解压缩到指定的文件夹。 打开终端,输入 zip -er <zipfile> &…...
【Acwing 周赛复盘】第92场周赛复盘(2023.2.25)
【Acwing 周赛复盘】第92场周赛复盘(2023.2.25) 周赛复盘 ✍️ 本周个人排名:1293/2408 AC情况:1/3 这是博主参加的第七次周赛,又一次体会到了世界的参差(这次周赛记错时间了,以为 19:15 开始&…...

L1-087 机工士姆斯塔迪奥
在 MMORPG《最终幻想14》的副本“乐欲之所瓯博讷修道院”里,BOSS 机工士姆斯塔迪奥将会接受玩家的挑战。 你需要处理这个副本其中的一个机制:NM 大小的地图被拆分为了 NM 个 11 的格子,BOSS 会选择若干行或/及若干列释放技能,玩家…...

本周大新闻|索尼PS VR2立项近7年;传腾讯将引进Quest 2
本周大新闻,AR方面,传立讯精密开发苹果初代AR头显,第二代低成本版将交给富士康;iOS 16.4代码曝光新的“计算设备”;EM3推出AR眼镜Stellar Pro;努比亚将在MWC2023推首款AR眼镜。VR方面,传闻腾讯引…...
aws console 使用fargate部署aws服务快速跳转前端搜索栏
测试过程中需要在大量资源之间跳转,频繁的点击不如直接搜索来的快,于是写了一个搜索框方便跳转。 前端的静态页面可以通过s3静态网站托管实现,但是由于中国区需要备案的原因,可以使用ecs fargate部署 步骤如下: 编写…...

Redis实战之Redisson使用技巧详解
一、摘要什么是 Redisson?来自于官网上的描述内容如下!Redisson 是一个在 Redis 的基础上实现的 Java 驻内存数据网格客户端(In-Memory Data Grid)。它不仅提供了一系列的 redis 常用数据结构命令服务,还提供了许多分布…...

SQLAlchemy
文章目录SQLAlchemy介绍SQLAlchemy入门使用原生sql使用orm外键关系一对多关系多对多关系基于scoped_session实现线程安全简单表操作实现方案CRUDFlask 集成 sqlalchemySQLAlchemy 介绍 SQLAlchemy是一个基于Python实现的ORM框架。该框架建立在 DB API之上,使用关系…...
【Linux学习笔记】8.Linux yum 命令和apt 命令
前言 本章介绍Linux的yum命令和apt命令。 Linux yum 命令 yum( Yellow dog Updater, Modified)是一个在 Fedora 和 RedHat 以及 SUSE 中的 Shell 前端软件包管理器。 基于 RPM 包管理,能够从指定的服务器自动下载 RPM 包并且安装…...
windows服务器实用(4)——使用IIS部署网站
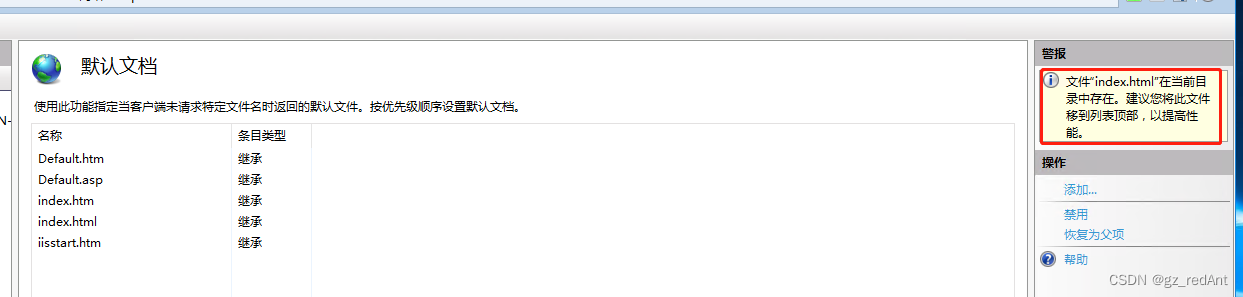
windows服务器实用——IIS部署网站 如果把windows服务器作为web服务器使用,那么在这个服务器上部署网站是必须要做的事。在windows服务器上,我们一般使用IIS部署。 假设此时前端给你一个已经完成的网站让你部署在服务器上,别人可以在浏览器…...
Random(二)什么是伪共享?@sun.misc.Contended注解
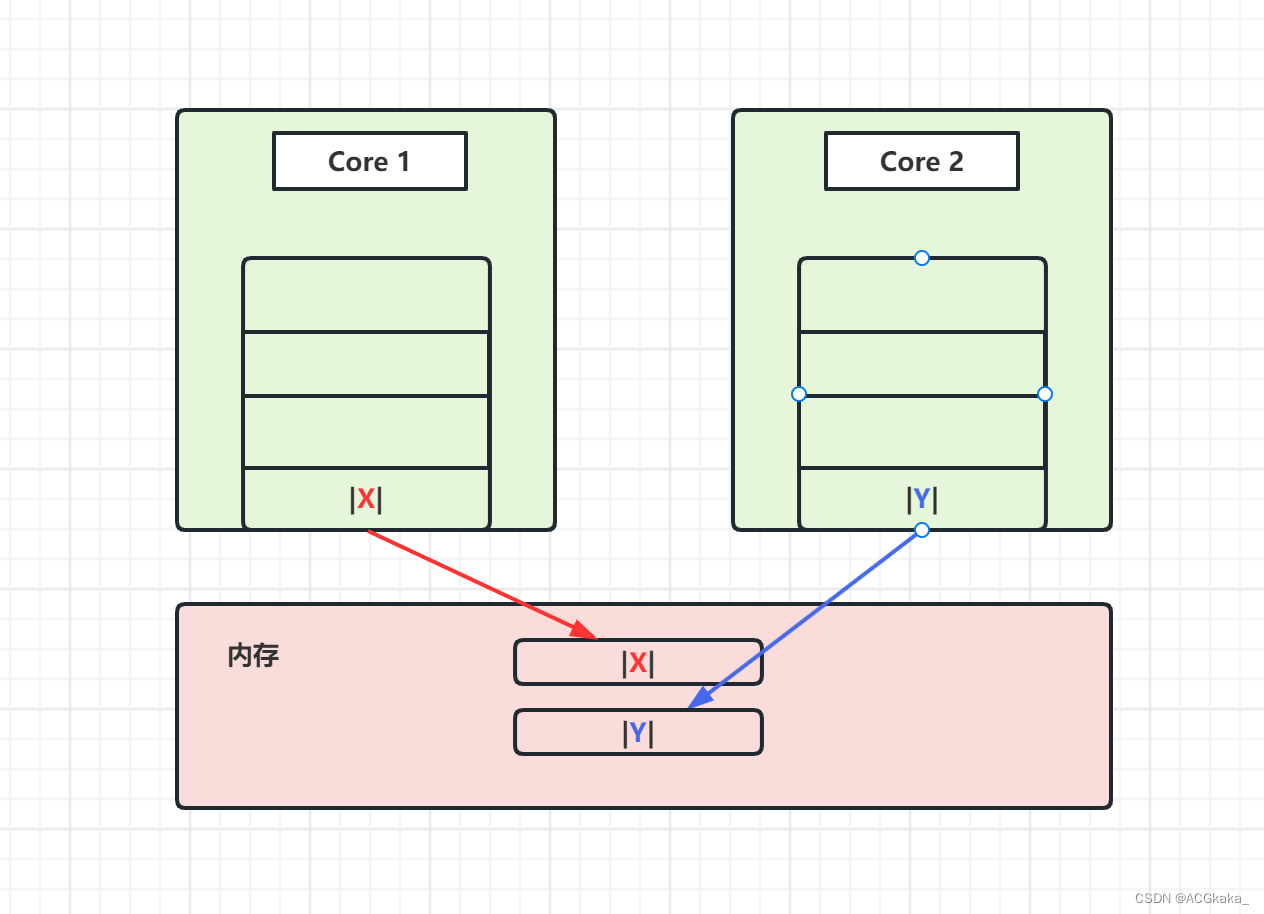
目录1.背景简介2.伪共享问题3.问题解决4.JDK使用示例1.背景简介 我们知道,CPU 是不能直接访问内存的,数据都是从高速缓存中加载到寄存器的,高速缓存又有 L1,L2,L3 等层级。在这里,我们先简化这些复杂的层级…...

Linux解压压缩
打包tar首先我们得提一下专门用于打包文件的命令——tartar用于备份文件,打包多个文件或者目录,也可以用于还原被打包的文件假设打包目录test下的文件 tar -cvf test.tar ./test 假设打包目录test下的文件,并用gzip命令将包压缩 tar -zcvf test.tar ./te…...

JavaSe第3次笔记
1.String str "hello";字符串类型。 2.两个字符串类型相加意思是拼接,类似于c语言里面的strcat函数。 3.整型变成字符串类型: int a 10; String str String. valueOf(a); 4.当字符串和其他类型进行相加的时候,结果就是字符串。(不完全…...

非人工智能专业怎样从零开始学人工智能?
人工智能(Artificial Intelligence,AI)是指让机器具有类似人类智能的能力,包括感知、理解、推理、学习、规划、决策、创造等多个方面。人工智能研究涉及到计算机科学、数学、物理学、心理学、哲学等多个领域,旨在模拟和…...

MyBatis之增、删、查、改
目录 前言 一、配置MyBatis开发环境 1.1 创建数据库和表 1.2 添加框架支持 1.3 创建目录结构 1.4 配置数据库连接 1.5 配置MyBatis中的XML文件路径 二、添加业务代码 2.1 查询数据库操作 2.1.1 添加实体类 2.1.2 添加mapper接口 2.1.3 在xml中实现mapper接口 2.1.…...
死磕Spring,什么是SPI机制,对SpringBoot自动装配有什么帮助
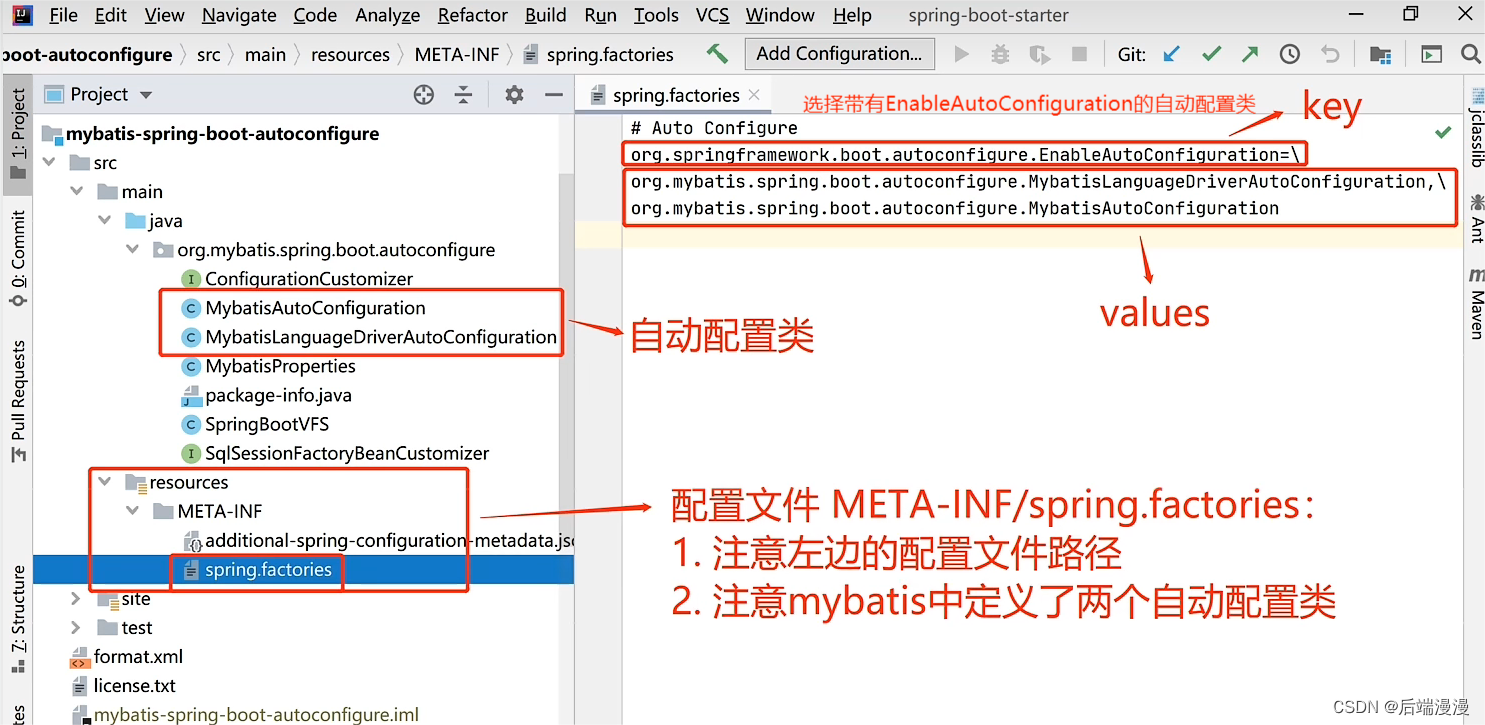
文章目录如果没时间看的话,在这里直接看总结一、Java SPI的概念和术语二、看看Java SPI是如何诞生的三、Java SPI应该如何应用四、从0开始,手撸一个SPI的应用实例五、SpringBoot自动装配六、Spring SPI机制与Spring Factories机制做对比七、这里是给我自…...
因果推断10--一种大规模预算约束因果森林算法(LBCF)
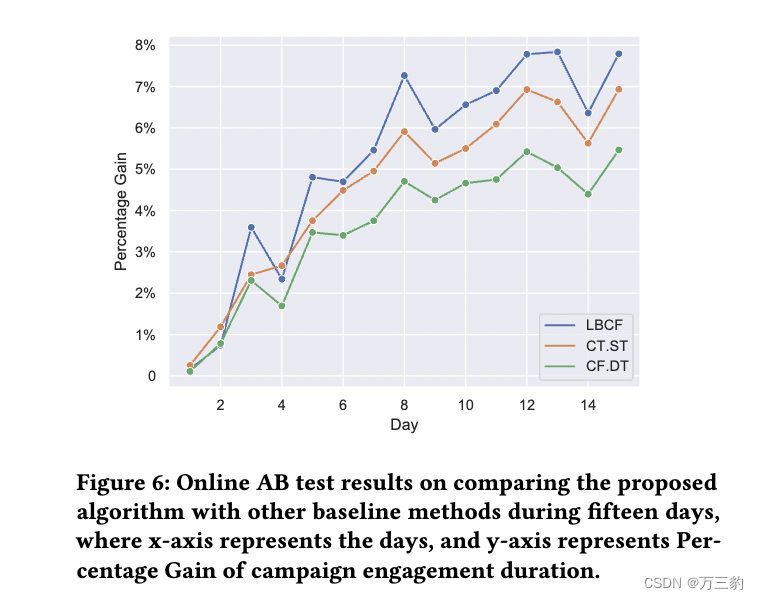
论文:A large Budget-Constrained Causal Forest Algorithm 论文:http://export.arxiv.org/pdf/2201.12585v2.pdf 目录 0 摘要 1 介绍 2 问题的制定 3策略评价 4 方法 4.1现有方法的局限性。 4.2提出的LBCF算法 5验证 5.1合成数据 5.2离线生…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
