【每日一题】补档 CF487B. Strip | 数据结构杂烩 -> 单调队列 | 困难
题目内容
原题链接
给定一个长度为 n n n 的数组,将这个数组进行拆分成若干个连续子数组,
使得每个子数组的最大值减去最小值小于等于 s s s ,
且每个子数组的长度大于等于 l e n len len 。
问最少可以拆分成多少个连续子数组,如果不可以,则输出 − 1 -1 −1
数据范围
- 1 ≤ n , l e n ≤ 1 0 5 1\leq n,len\leq 10^5 1≤n,len≤105
- 0 ≤ s ≤ 1 0 9 0\leq s\leq 10^9 0≤s≤109
- − 1 0 9 ≤ a i ≤ 1 0 9 -10^9\leq a_i\leq 10^9 −109≤ai≤109
题解
状态定义
d p [ i ] dp[i] dp[i] 表示将前 i i i 个数可以拆分出的最少的连续子数组。
状态转移
d p [ i ] = min { d p [ j ] } + 1 dp[i]= \min\{dp[j]\}+1 dp[i]=min{dp[j]}+1
这里需要满足如下两个条件:
1. max { a [ j + 1 , ⋯ , i ] } − min { a [ j + 1 , ⋯ , i ] } ≤ s 1. \max\{a[j+1,\cdots,i]\}-\min\{a[j+1,\cdots,i]\}\leq s 1.max{a[j+1,⋯,i]}−min{a[j+1,⋯,i]}≤s
2. i − j + 1 ≥ l e n 2. i-j+1\geq len 2.i−j+1≥len
暴力做法
直接枚举所有的 j j j
时间复杂度: O ( n 2 ) O(n^2) O(n2)
优化做法1
考虑如何加速找到所有合法的 j j j
当 j j j 越小,即 [ j + 1 , i ] [j+1,i] [j+1,i] 这个区间的最大值越大,最小值越小,那么就极值之差就越有可能大于等于 s s s 。
那么这部分就是满足二段性的,如此就可以二分。
右端点为 i i i ,二分左端点 j j j ,那么 [ j , i ] [j, i] [j,i] 的区间极值之差如果大于 s s s ,那么左端点应该更大,否则应该继续二分尝试减小左端点。
如此二分的时候应该快速找到区间极值,这部分用 R M Q RMQ RMQ 来解决。
我们最终二分出的左端点为 j j j ,那么需要找到区间 [ j − 1 , i − l e n ] [j-1, i-len] [j−1,i−len] 中的 d p dp dp 最小值。这部分因为是动态区间求最值,线段树或者优先队列懒 pop 来解决。
时间复杂度: O ( n log n ) O(n\log n) O(nlogn)
优化做法2
考虑到这里很多都是求区间的极值,而且对于每个右端点,其左端点一定是单调不减的,所以可以考虑双指针。
枚举右端点 r r r,然后移动左端点 l l l,使得区间最大值减去最小值小于等于 s s s 。
q m a x qmax qmax 是一个单调递减的队列,队头存储的是区间最大值
q m i n qmin qmin 是一个单调递增的队列,队头存储的是区间最小值
如此就可以 O ( 1 ) O(1) O(1) 快速查出区间极值。
此外,我们还需要知道最终得到左端点 l l l ,区间 [ l − 1 , r − l e n ] [l-1,r-len] [l−1,r−len] 的 d p dp dp 最小值。这部分同样可以用一个单调递增的队列来维护。
时间复杂度: O ( n ) O(n) O(n)
优化做法1代码一
#include <bits/stdc++.h>
using namespace std;const int N = 100010;
const int INF = 0x3f3f3f3f;
const int BIT = 17;int qmax[BIT][N];
int qmin[BIT][N];
int lg[N];
int a[N];
int n, s, len;
int dp[N];void init_rmq() {for (int i = 2; i <= n; ++i) lg[i] = lg[i >> 1] + 1;for (int j = 1; j <= n; ++j) qmax[0][j] = qmin[0][j] = a[j];for (int k = 1; k < BIT; ++k)for (int j = 1; j + (1 << k) - 1 <= n; ++j) {qmax[k][j] = max(qmax[k - 1][j], qmax[k - 1][j + (1 << (k - 1))]);qmin[k][j] = min(qmin[k - 1][j], qmin[k - 1][j + (1 << (k - 1))]);}
}int query_seg(int left, int right) {int bit = lg[right - left + 1];return max(qmax[bit][left], qmax[bit][right - (1 << bit) + 1]) - min(qmin[bit][left], qmin[bit][right - (1 << bit) + 1]);
};struct Node {int l, r;int val;
}tr[N << 2];void build(int u, int l, int r) {tr[u] = {l, r, INF};if (l == r) return;int mid = (l + r) >> 1;build(u << 1, l, mid);build(u << 1 | 1, mid + 1, r);
}int query(int u, int l, int r) {if (tr[u].l >= l && tr[u].r <= r) {return tr[u].val;}int mid = (tr[u].l + tr[u].r) >> 1;int ans = INF;if (l <= mid) ans = min(ans, query(u << 1, l, r));if (r > mid) ans = min(ans, query(u << 1 | 1, l, r));return ans;
}void modify(int u, int p, int x) {if (tr[u].l == tr[u].r) {tr[u].val = x;return;}int mid = (tr[u].l + tr[u].r) >> 1;if (p <= mid) modify(u << 1, p, x);else modify(u << 1 | 1, p, x);tr[u].val = min(tr[u << 1].val, tr[u << 1 | 1].val);
}int main()
{scanf("%d%d%d", &n, &s, &len);for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);init_rmq();build(1, 0, n);// 考虑每个点 i 向左的最大值和最小值// 二分最短的,然后我需要知道这个区间里的最大值减最小值// dp[i] 表示前 i 个点需要拆分成的最少段for (int i = 1; i <= n; ++i) dp[i] = INF;dp[0] = 0;modify(1, 0, 0);for (int i = len; i <= n; ++i) {if (query_seg(i - len + 1, i) > s) continue;int left = 1, right = i - len + 1;while (left < right) {int mid = (left + right) >> 1;if (query_seg(mid, i) > s) left = mid + 1;else right = mid;}// 查 left - 1 到 i - len 的最小值dp[i] = min(dp[i], query(1, left - 1, i - len) + 1);// 单点最小值更新if (dp[i] < INF) {modify(1, i, dp[i]);}}printf("%d\n", dp[n] == INF ? -1 : dp[n]);return 0;
}
优化做法1代码二
#include <bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;
const int N = 100010;
const int INF = 0x3f3f3f3f;
const int BIT = 17;int qmax[BIT][N];
int qmin[BIT][N];
int lg[N];
int a[N];
int n, s, len;
int dp[N];void init_rmq() {for (int i = 2; i <= n; ++i) lg[i] = lg[i >> 1] + 1;for (int j = 1; j <= n; ++j) qmax[0][j] = qmin[0][j] = a[j];for (int k = 1; k < BIT; ++k)for (int j = 1; j + (1 << k) - 1 <= n; ++j) {qmax[k][j] = max(qmax[k - 1][j], qmax[k - 1][j + (1 << (k - 1))]);qmin[k][j] = min(qmin[k - 1][j], qmin[k - 1][j + (1 << (k - 1))]);}
}int query_seg(int left, int right) {int bit = lg[right - left + 1];return max(qmax[bit][left], qmax[bit][right - (1 << bit) + 1]) - min(qmin[bit][left], qmin[bit][right - (1 << bit) + 1]);
};int main()
{scanf("%d%d%d", &n, &s, &len);for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);init_rmq();// 考虑每个点 i 向左的最大值和最小值// 二分最短的,然后我需要知道这个区间里的最大值减最小值// dp[i] 表示前 i 个点需要拆分成的最少段for (int i = 1; i <= n; ++i) dp[i] = INF;dp[0] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;for (int i = len; i <= n; ++i) {if (i == 5) {int x = 1;}if (dp[i - len] < INF) {heap.emplace(dp[i - len], i - len);}if (query_seg(i - len + 1, i) > s) continue;int left = 1, right = i - len + 1;while (left < right) {int mid = (left + right) >> 1;if (query_seg(mid, i) > s) left = mid + 1;else right = mid;}// 查 left - 1 到 i - len 的最小值while (!heap.empty() && heap.top().second < left - 1) {heap.pop();}if (!heap.empty()) {dp[i] = heap.top().first + 1;}}printf("%d\n", dp[n] == INF ? -1 : dp[n]);return 0;
}
优化做法2代码
#include <bits/stdc++.h>
using namespace std;const int N = 100010;
const int INF = 0x3f3f3f3f;
int n, s, len;
int a[N];
int dp[N];
struct Queue {int q[N]{};int hh, tt;Queue(): hh(0), tt(-1) {}void push(int x) { q[++tt] = x; }void pop_back() { --tt; }void pop_front() { ++hh; }bool empty() const { return hh > tt; }int front() const { return q[hh]; }int back() const { return q[tt]; }
}qmax, qmin, qdp;int main()
{scanf("%d%d%d", &n, &s, &len);for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);memset(dp, 0x3f, (n + 1) * sizeof(int));dp[0] = 0;for (int r = 1, l = 1; r <= n; ++r) {// 找到这个区间里的最小值while (!qmin.empty() && a[qmin.back()] >= a[r]) qmin.pop_back();qmin.push(r);// 找到这个区间里的最大值while (!qmax.empty() && a[qmax.back()] <= a[r]) qmax.pop_back();qmax.push(r);// 此时区间 [l, r] 里的最小值和最大值都已确定// 我们需要使得挪动左端点,直到区间 max - min <= s// 挪动左端点就意味着 qmax 和 qmin 需要进行移动,使得 qmax 和 qmin 的值都是在 [l, r] 之间while (!qmin.empty() && !qmax.empty() && a[qmax.front()] - a[qmin.front()] > s) {l += 1;while (!qmin.empty() && qmin.front() < l) qmin.pop_front();while (!qmax.empty() && qmax.front() < l) qmax.pop_front();}if (r >= len && dp[r - len] < INF) {while (!qdp.empty() && dp[qdp.back()] >= dp[r - len]) qdp.pop_back();qdp.push(r - len);}while (!qdp.empty() && qdp.front() < l - 1) qdp.pop_front();if (r - l + 1 >= len && !qdp.empty()) {dp[r] = dp[qdp.front()] + 1;}}printf("%d\n", dp[n] == INF ? -1 : dp[n]);return 0;
}
相关文章:

【每日一题】补档 CF487B. Strip | 数据结构杂烩 -> 单调队列 | 困难
题目内容 原题链接 给定一个长度为 n n n 的数组,将这个数组进行拆分成若干个连续子数组, 使得每个子数组的最大值减去最小值小于等于 s s s , 且每个子数组的长度大于等于 l e n len len 。 问最少可以拆分成多少个连续子数组࿰…...

向量数据库和普通关系型数据库的区别,LAXCUS支持哪种数据库?
这是一位Laxcus用户在后台的提问,贴出来供大家参考: 1. 向量数据库与传统的关系型数据库主要有以下几个区别: 数据类型:向量数据库专门用于存储和查询向量数据,而传统数据库可以存储各种类型的数据,如文本…...

操作系统 --- 存储器管理
一、简答题 1.存储器管理的基本任务,是为多道程序的并发执行提供良好的存储器环境。请问好的存储器环境”应包含哪几个方面? 答: 2.内存保护是否可以完全由软件实现?为什么? 答:内存保护的主要任务是确保每…...

Python selenium无界面headless
视频版教程:一天掌握python爬虫【基础篇】 涵盖 requests、beautifulsoup、selenium Chrome-headless 模式, Google 针对 Chrome 浏览器 59版 新增加的一种模式,可以让你不打开UI界面的情况下使用 Chrome 浏览器,所以运行效果与 …...

JavaScript 中的负无穷大是什么?
在 JavaScript 中,负无穷大表示为 -Infinity。它是一个特殊的数值,用于表示比任何实数都要小的值。 负无穷大用于表示超出数值范围的情况,例如在进行数学计算时发生了溢出或出现了无法表示的结果。它可以通过将负无穷大赋值给变量或通过某些…...

2023年十大地推和网推拉新app推广接单平台,一手单渠道
做地推最重要的一定是找好项目,找好项目最关键的一定是地推app接任务平台,所以这十大靠谱的地推拉新接单平台,都是我们精心筛选的,2023年从事地推和网推拉新作业。 1:聚量推客 “聚量推客”汇聚了众多市场上有的和没有…...

mybatis-plus的进阶使用
文章目录 自定义xml的sql脚本配置mybaits的全局配置文件mybatis-plus优化,指定select数据库乐观锁mybatis-plus实现数据库乐观锁mybatis-plus实现逻辑删除 自定义xml的sql脚本 这里的使用和mybatis一样 编写mapper.xml文件 <?xml version"1.0" enc…...

centos安装vim编辑器
第一步检查centos的vim编辑器包是否完整 rpm -qa|grep vim //查看Vim编辑器需要安装的四个包是否完整 第二步:一般安装vim编辑器需要一下四个安装包,缺失了之后可对应下载 vim-minimal-7.4.160-2.el7.x86_64vim-common-7.4.160-4.el7.x86_64 v…...
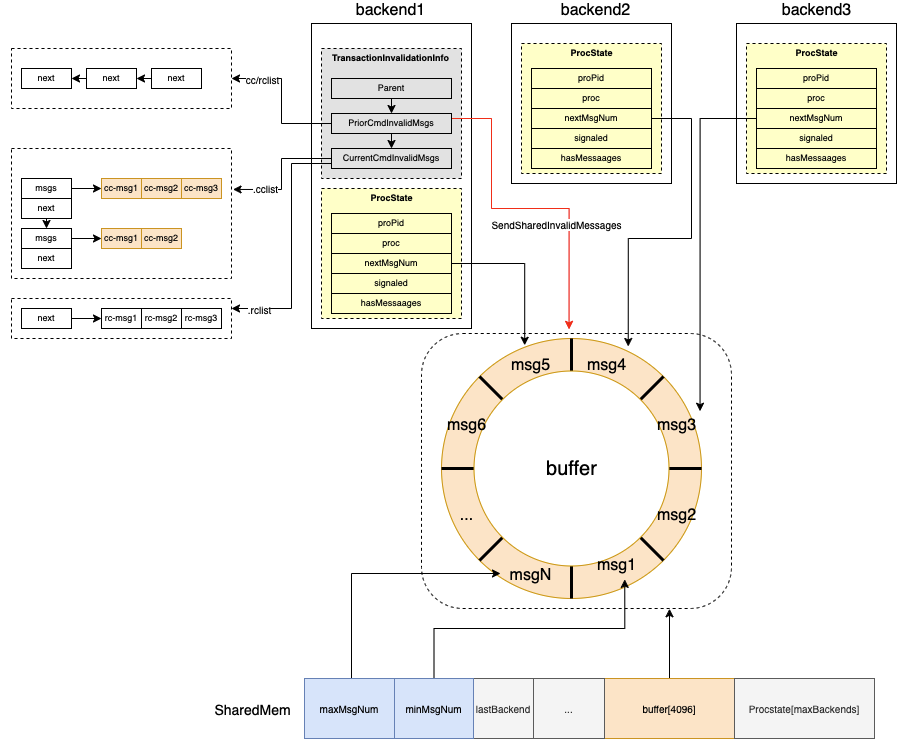
PostgreSQL InvalidMessage Cache 同步机制
文章目录 背景InvalidMessages 基本类型InvalidMessages 数据结构概览共享内存 的 "ring-buffer" 结构Backend 本地的 InvalidMessages管理SharedInvalCatalogMsgSharedInvalCatcacheMsgSharedInvalRelcacheMsgSharedInvalSnapshotMsgSharedInvalSmgrMsgSharedInvalR…...

C#,数值计算——Globals的计算方法与源程序
1 文本格式 using System; using System.Text; namespace Legalsoft.Truffer { public static partial class Globals { //const int FLT_RADIX 2; //const int DBL_MANT_DIG 53; //const int INT_DIGITS 32; //const float FLT_…...
腾讯云香港服务器轻量24元一个月性能测试
腾讯云香港轻量应用服务器优惠价格24元一个月,一年288元,以前是30M峰值带宽,现在是20M峰值带宽,阿腾云atengyun.com分享腾讯云香港轻量应用服务器性能测评,包括香港轻量服务器配置价格表、CPU性能和CN2网络延迟测试&am…...
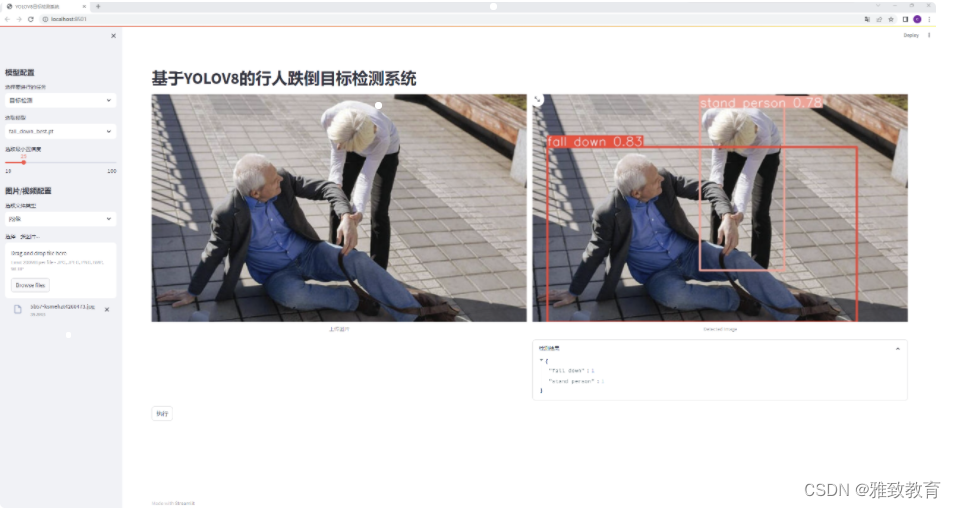
深度学习之基于YoloV8的行人跌倒目标检测系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、行人跌倒目标检测系统四. 总结 一项目简介 世界老龄化趋势日益严重,现代化的生活习惯又使得大多数老人独居,统计数据表…...

Seata入门系列【16】XA模式入门案例
1 前言 在之前,我们试过了AT、TCC 模式,Seata 还支持XA 模式。 2 XA 协议 XA协议由Tuxedo首先提出的,并交给X/Open组织,作为资源管理器(数据库)与事务管理器的接口标准。Oracle、Informix、DB2和Sybase等…...
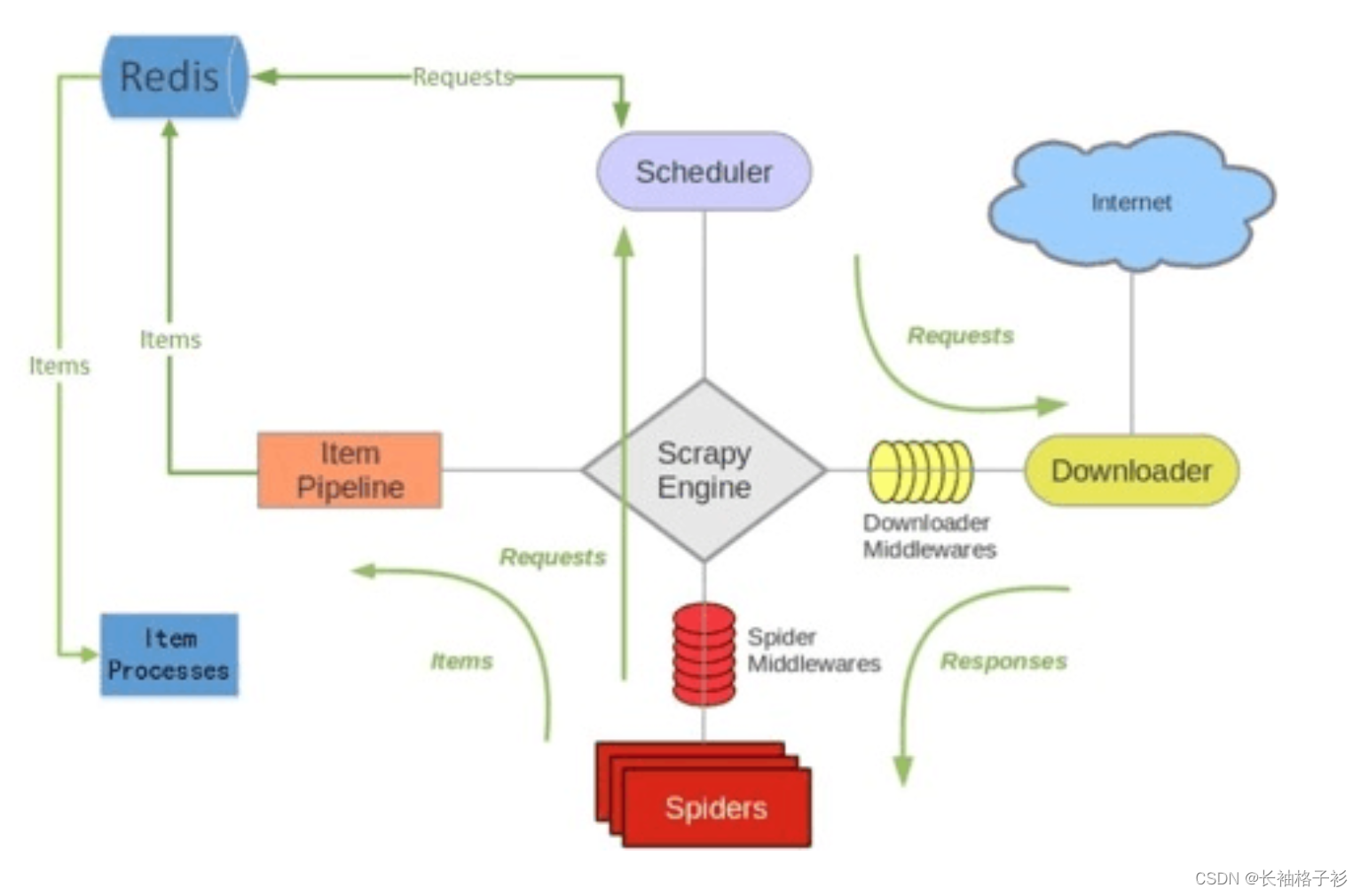
高级深入--day44
Scrapy 和 scrapy-redis的区别 Scrapy 是一个通用的爬虫框架,但是不支持分布式,Scrapy-redis是为了更方便地实现Scrapy分布式爬取,而提供了一些以redis为基础的组件(仅有组件)。 pip install scrapy-redis Scrapy-redis提供了下面四种组件&a…...

Apache Doris (四十八): Doris表结构变更-替换表
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录...
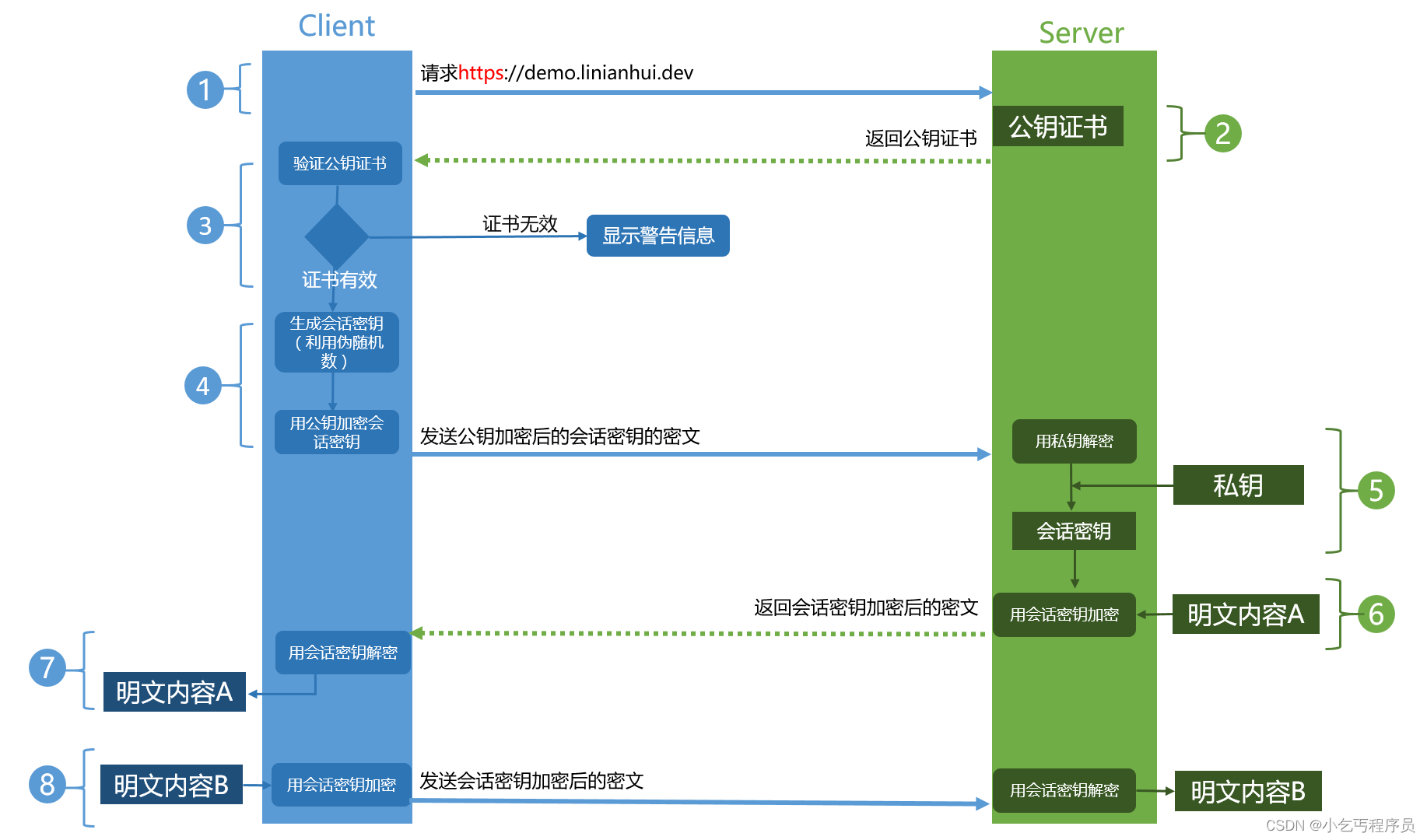
消息认证码--数字签名--证书
6. 消息认证码—>保证数据的完整性 "消息认证码 --- 消息被正确传送了吗?"6.1 什么是消息认证码 Alice 和 Bob 的故事 像以前一样,我们还是从一个Alice和Bob的故事开始讲起。不过,这一次Alice和Bob分别是两家银行,Alice银行通…...

四个制作PPT的小技巧
制作PPT已经很麻烦了,学习一些小技巧可以帮助我们省时省力吧! 技巧一:自动更新日期和时间 当我们给幻灯片添加了页脚并且是时间日期,可以通过设置达到自动更新,这样我们就不需要每次修改的时候都要手动更新日期和时间…...

Echarts饼状图grid设置
饼状图不能设置grid,而是center {type: "pie",radius: ["30%", "70%"],center: ["50%", "25%"], }center 圆心:控制圆的位置 radius 饼图的半径 控制显示尺寸 参考文章 Echarts饼状图设置...

系列三、Spring IOC
一、概述 IOC的中文意思是控制反转,通俗地讲就是把创建对象的控制权交给了Spring去管理,以前是由程序员自己去创建控制对象,现在交由Spring去创建控制。 二、优点 集中管理对象,方便维护,降低耦合度。 三、IOC的底层…...

electron汇总
python3自带了pip pip search已经被禁用,安装pip—— pip install pip-searchpython3.x移除了distutils 管理员权限下运行cmd,运行以下命令 // 修改pip镜像地址 pip config set global.index-url https://mirrors.aliyun.com/pypi/simple/ // 安装 Set…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
