当前位置： 首页 > news >正文

电脑入门：电脑专业英语500词，供新手参考

news 2025/12/20 21:35:48

1. file n. 文件；v. 保存文件 
2. command n. 命令，指令 
3. use v. 使用，用途 
4. program n. 程序 
5. line n. (数据，程序)行，线路 
6. if conj. 如果 
7. display vt. 显示，显示器 
8. set v. 设置，n. 集合 
9. key n. 键，关键字，关键码 
10. list n. 列表，显示，v. 打印 
11. by prep. 凭，**，沿 
12. press v. 按，压 
13. with prep. 用，与，随着 
14. format n. 格式 
15. change v. 更换，改变，变动 
16. cursor n. 光标 
17. directory n. 目录，索引簿 
18. from prep. 从，来自，以来 
19. menu n. 菜单，目录 
20. option n. 任选，选择，可选项 
21. character n. 字符，符号，特性 
22. current n. 电流 
23. type n. 型，类型；v. 打印 
24. screen n. 屏幕，屏；v. 屏蔽 
25. specify v. 指定，规定，确定 
26. move v. 移动 
27. disk n. 盘，磁盘 
28. text n. 正文，文本 <

相关文章：

电脑入门：电脑专业英语500词，供新手参考

1. file n. 文件；v. 保存文件 2. command n. 命令，指令 3. use v. 使用，用途 4. program n. 程序 5. line n. (数据，程序)行，线路 6. if conj. 如果 7. display vt. 显示，显示器 8. set v. 设置，n. 集合 9. key n. 键，关键字，关键码 10. list n. 列表，显示，…...

编程日记 2023/10/30 13:10:38

采购管理工具-采购软件-Leangoo免费看板工具

我们可以按照公司的实际情况定制采购流程。 1、在Leangoo免费看板工具中创建一个项目&#xff0c;项目类型建议选择“轻量级协作”&#xff0c;项目模版建议选择“人事与行政” 系统会自动为您创建四个看板&#xff0c;如下图&#xff1a; 图1 2、在项目内创建一个 “办公室采…...

编程日记 2023/10/30 13:09:37

【23真题】大神凭这套拿452分！看看你能拿多少？

今天分享的是23年福州大学866的信号与系统试题及解析。23年福州大学新一代电子信息的最高分是452分&#xff01;但是我看不到单科分数。按照75&#xff0c;75&#xff0c;150&#xff0c;150。也就是只有450&#xff0c;说明这个同学&#xff0c;专业课和数学几乎拿满&#xff…...

编程日记 2023/10/30 13:08:35

大数据之LibrA数据库系统告警处理（ALM-12002 HA资源异常）

告警解释 HA软件周期性检测Manager的WebService浮动IP地址和数据库。当HA软件检测到浮动IP地址或数据库异常时&#xff0c;产生该告警。 当HA检测到浮动IP地址或数据库正常后&#xff0c;告警恢复。 告警属性 告警参数 对系统的影响 如果Manager的WebService浮动IP地址异常…...

编程日记 2023/10/30 13:06:31

CSS基础入门04

目录 1.内边距 1.1基础写法 1.2复合写法 2.外边距 2.1基础写法 2.2复合写法 2.3块级元素水平居中 3.去除浏览器默认样式 4.弹性布局 4.1初体验 5.flex 布局基本概念 6.常用属性 6.1justify-content 6.2align-items 1.内边距 padding 设置内容和边框之间的距离. …...

编程日记 2023/10/30 13:05:31

LeetCode2741.特别的排列 状压

暴力枚举的话是n&#xff01; 考虑状压DP&#xff0c;其实就是用二进制表示状态 再进行暴力 同时加一个记忆化就好了 这里有常用技巧&#xff1a; 全集&#xff08;1<<n&#xff09;-1 增加某个元素 x | (1<<i) 删除某个元素 x & ~(1<<i) const i…...

编程日记 2023/10/30 13:04:28

【Linux】Centos 8 服务器部署：阿里云域名注册、域名解析、个人网站 ICP 备案详细教程

目录 一、背景信息 二、操作步骤 &#xff08;1&#xff09;查询域名 &#xff08;2&#xff09;加入域名清单 &#xff08;3&#xff09;确认订单信息 &#xff08;4&#xff09;支付 &#xff08;5&#xff09;等待域名实名认证通过 三、域名注册成功 四、查看域名…...

编程日记 2023/10/30 13:02:27

Sass、Less和Stylus之间有什么主要的区别？

Sass、Less和Stylus是三种常见的CSS预处理器&#xff0c;它们在功能和语法上有一些区别。以下是它们之间的主要区别&#xff1a; 1&#xff1a;语法差异&#xff1a; Sass使用缩进的语法&#xff0c;使用类似于Python的缩进来表示嵌套规则和块级作用域。Less和Stylus使用类似…...

编程日记 2023/10/30 13:00:25

第八章 软件测试自动化

一、学习目的与要求 通过本章的学习&#xff0c;了解自动化测试应考虑的各种因素及如何衡量自动化测试成本&#xff0c;掌握自动化测试和手工测试的优缺点&#xff0c;能正确选择软件测试策略&#xff0c;了解测试工 具的分类和使用目的&#xff0c;熟悉常用的测试工具&#xf…...

编程日记 2023/10/30 12:57:20

科大讯飞勾勒生成式AI输入法“模样”，开启下一代输入法革命

回顾国内第三方输入法赛道近十余年的发展&#xff0c;移动互联网的市场红利催生了科大讯飞、百度、搜狗等颇具规模和实力的头部厂商。与此同时&#xff0c;历经多年、多方角逐&#xff0c;第三方输入法市场进入存量阶段&#xff0c;升级技术、优化用户体验来挖掘存量&#xff0…...

编程日记 2023/10/30 12:56:18

OV-VG: A Benchmark for Open-Vocabulary Visual Grounding

OV-VG: A Benchmark for Open-Vocabulary Visual Grounding 一、Abstract 写在前面 又是一周周末&#xff0c;光调代码去了&#xff0c;都没时间看论文了&#xff0c;汗。   这是一篇关于开放词汇定位的文章&#xff0c;也是近两年的新坑&#xff0c;但是资源也是需要不少。 …...

编程日记 2023/10/30 12:55:17

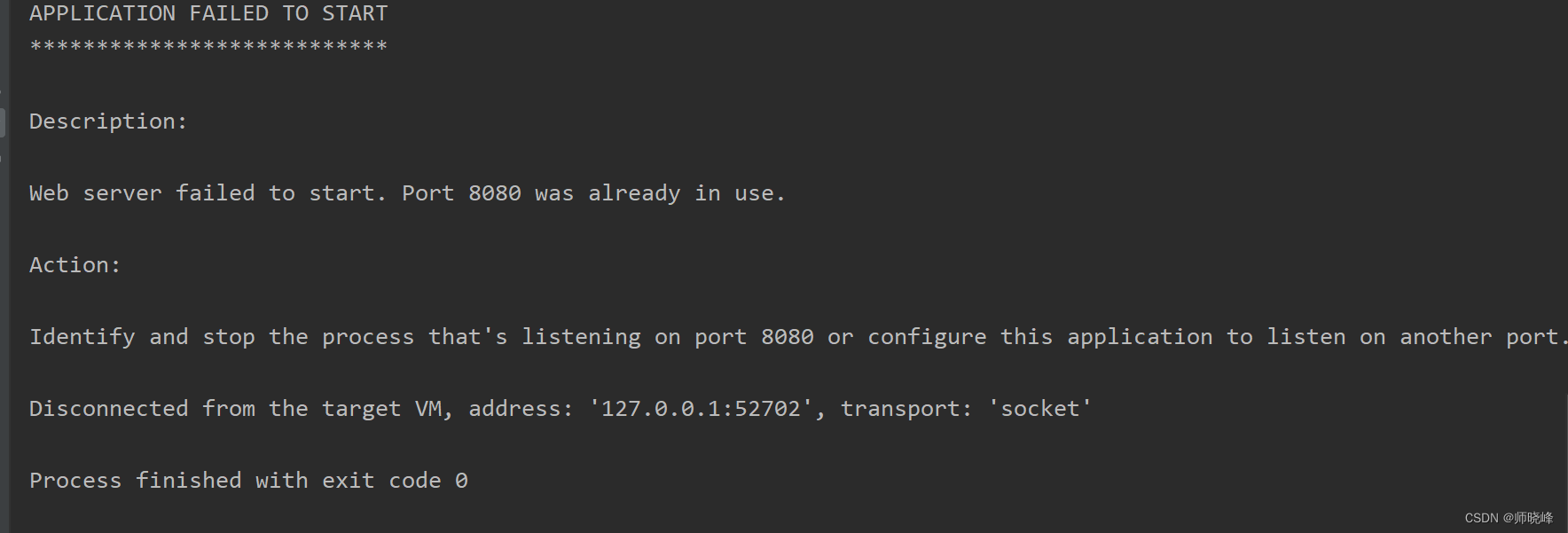
win10 javaweb 项目8080端口被占用

文章目录 前言出现场景&#xff1a;解决思路&#xff1a; 前言 提示&#xff1a;生活该走向何处&#xff1f;也许你还不知道答案&#xff0c;但是你一定是答案的一部分。 出现场景&#xff1a; 解决思路&#xff1a; 找到运行的进程直接干掉 打开命令窗口&#xff08;win r…...

编程日记 2023/10/30 12:54:16

C语言每日一题（22）合并两个有序数组

力扣网 88. 合并两个有序数组 题目描述 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2&#xff0c;另有两个整数 m 和 n &#xff0c;分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中&#xff0c;使合并后的数组同样按 非递减顺序 排列。 注意…...

编程日记 2023/10/30 12:53:14

C++学习day--24 推箱子游戏图像化开发

环境要求&#xff1a; 1、VS2015以上 2、成功安装并配置图形库 项目注意事项&#xff1a;代码复制好以后&#xff0c;把下面的字符集改为多字节字符集 第 1 节 项目需求 实现一款推箱子游戏&#xff0c;效果如下图所示 , 具体规则&#xff1a; 1. 箱子只能推动而不能拉动…...

编程日记 2023/10/30 12:52:12

YOLOv8中的After Fuse指的是什么？

Fuse是指模型的一些模块进行融合。常见的就是conv和bn层进行融合,在训练的时候模型是存在conv和bn的,但在推理的过程中,模型在初始化的时候会进行模型fuse,把其中的conv和bn进行融合,通过一些数学转换把bn层融合到conv里面,还有一些例如DBB,RepVGG等等模块支持融合的这些在fuse…...

编程日记 2023/10/30 12:50:11

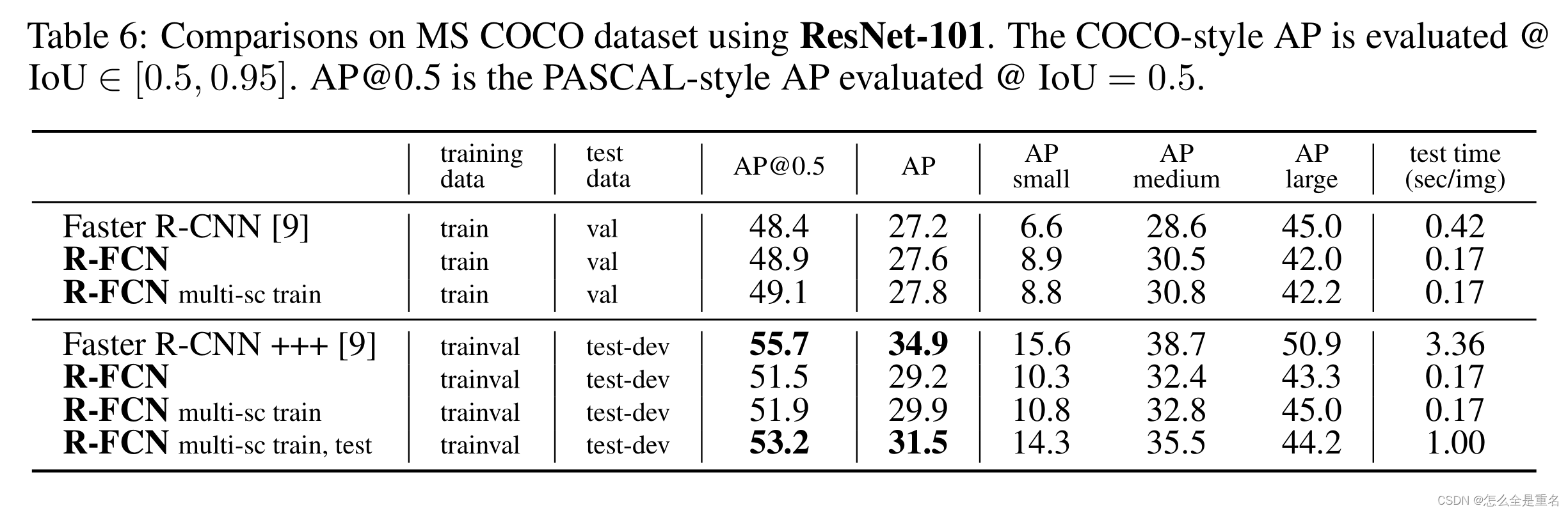
R-FCN: Object Detection via Region-based Fully Convolutional Networks（2016.6）

文章目录 AbstractIntroduction当前最先进目标检测存在的问题针对上述问题&#xff0c;我们提出... Our approachOverviewBackbone architecturePosition-sensitive score maps & Position-sensitive RoI pooling Related WorkExperimentsConclusion 原文链接 源代码 Abstr…...

编程日记 2023/10/30 12:49:09

Linux服务器部署Spring Boot项目的一些shell命令脚本

1.启动jar包的命令&#xff08;根据jar包数量创建&#xff0c;并指定相对应的jar包&#xff09; nohup java -server -Xms64m -Xmx128m -jar 项目jar包的名称.jar --spring.profiles.activeprod > 记录jar包的日志.log 2>&1 &可以写在start.sh文件里&#xff08…...

编程日记 2023/10/30 12:42:59

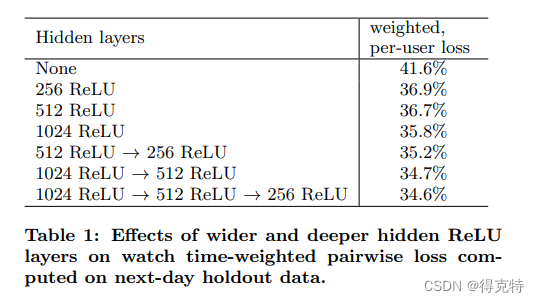
Youtube DNN：Deep Neural Networks for YouTube Recommendations

1.介绍 本文主要解决的三个挑战&#xff1a; 大规模的推荐场景&#xff0c;能够支持分布式训练和提供有效率的服务。不断更新的新物料。稀疏的用户行为&#xff0c;包含大量的噪声。 2.推荐系统 文章包含推荐系统的两阶段模型&#xff1a;召回和排序。 召回网络根据用户的历…...

编程日记 2023/10/30 12:41:57

Python 入门基础知识点有哪些？

Python是一种高级的、解释性的、面向对象的、动态类型语言&#xff0c;它在机器学习、数据分析、Web开发、科学计算等领域都有广泛的应用。下面是Python入门基础知识点的详细介绍。 1、变量和数据类型 在Python中&#xff0c;可以使用变量来存储数据。Python的数据类型包括整…...

编程日记 2023/10/30 12:40:57

【每日一题】补档 CF487B. Strip | 数据结构杂烩 -＞ 单调队列 | 困难

题目内容 原题链接 给定一个长度为 n n n 的数组&#xff0c;将这个数组进行拆分成若干个连续子数组&#xff0c; 使得每个子数组的最大值减去最小值小于等于 s s s &#xff0c; 且每个子数组的长度大于等于 l e n len len 。 问最少可以拆分成多少个连续子数组&#xff0…...

编程日记 2023/10/30 12:38:55

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2025/8/27 13:05:41

AI Agent与Agentic AI：原理、应用、挑战与未来展望

文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例&#xff1a;使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例&#xff1a;使用OpenAI GPT-3进…...

编程新知 2025/12/19 6:16:09

【解密LSTM、GRU如何解决传统RNN梯度消失问题】

解密LSTM与GRU&#xff1a;如何让RNN变得更聪明&#xff1f; 在深度学习的世界里&#xff0c;循环神经网络&#xff08;RNN&#xff09;以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而&#xff0c;传统RNN存在的一个严重问题——梯度消失&#…...

编程新知 2025/12/14 16:14:14

2024年赣州旅游投资集团社会招聘笔试真

2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案，答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年，()预言了电磁波的存在，并指出…...

编程新知 2025/12/10 4:08:53

渲染学进阶内容——模型

最近在写模组的时候发现渲染器里面离不开模型的定义，在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容，其实不管是方块还是方块实体，都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器，用于动态创…...

编程新知 2025/11/25 22:59:17

Neo4j 集群管理：原理、技术与最佳实践深度解析

Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档，本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石，用于构建高可用、可扩展且一致的图数据库服务…...

编程新知 2025/12/11 3:51:27

多种风格导航菜单 HTML 实现（附源码）

下面我将为您展示 6 种不同风格的导航菜单实现&#xff0c;每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

编程新知 2025/12/17 14:12:41

C++八股 —— 单例模式

文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全&#xff08;Thread Safety&#xff09; 线程安全是指在多线程环境下&#xff0c;某个函数、类或代码片段能够被多个线程同时调用时&#xff0c;仍能保证数据的一致性和逻辑的正确性&#xf…...

编程新知 2025/12/2 3:35:50

是否存在路径（FIFOBB算法）

题目描述 一个具有 n 个顶点e条边的无向图&#xff0c;该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序&#xff0c;确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数&#xff0c;分别表示n 和 e 的值&#xff08;1…...

编程新知 2025/10/1 6:09:21

Unity | AmplifyShaderEditor插件基础（第七集：平面波动shader）

目录 一、&#x1f44b;&#x1f3fb;前言 二、&#x1f608;sinx波动的基本原理 三、&#x1f608;波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、&#x1f30a;波动优化…...

编程新知 2025/12/9 15:19:40