并查集(13张图解)--擒贼先擒王
目录
前言
故事
🌼思路
🌼总结
🌼代码
👊观察过程代码
👊正确代码
👊细节代码
来自《啊哈算法》
前言
刚学了树在优先队列中的应用--堆的实现
那么树还有哪些神奇的用法呢?我们从一个故事说起----揭秘犯罪团伙

故事
快过年了,犯罪分子们也开始为年终奖“奋斗”了,小哼的家乡出现多次抢劫事件。
由于强盗人数过于庞大,作案频繁,警察想调查清楚到底有几个犯罪团伙实在不容易。
不过警察叔叔还是搜集到了几条线索
现在有10个强盗,9条线索

1--2(表示1号强盗与2号强盗是同伙)
3--4,5--2,4--6,2--6,8--7,9--7,1--6,2--4
规定,强盗同伙的同伙也是同伙,你能帮警察叔叔查出有多少个独立的犯罪团伙吗?
🌼思路
要解决这个问题,先假设10个强盗相互不认识,他们各自为政,每个人都是自己的头,只听自己的
之后,我们通过警察的线索,一步步“合并同伙”
1,声明一维数组
申请一个一维数组dad,dad[1] == 1表示1号强盗的头是自己,10号强盗的头是10号自己用dad[10] == 10表示
2,初始化
初始化dad数组(当然,书里是f数组) ,令 dad[i] = i; 即可

3,合并同伙
如果发现两个强盗是同伙,那么他俩是同一犯罪团伙,但是。。。谁做老大呢?
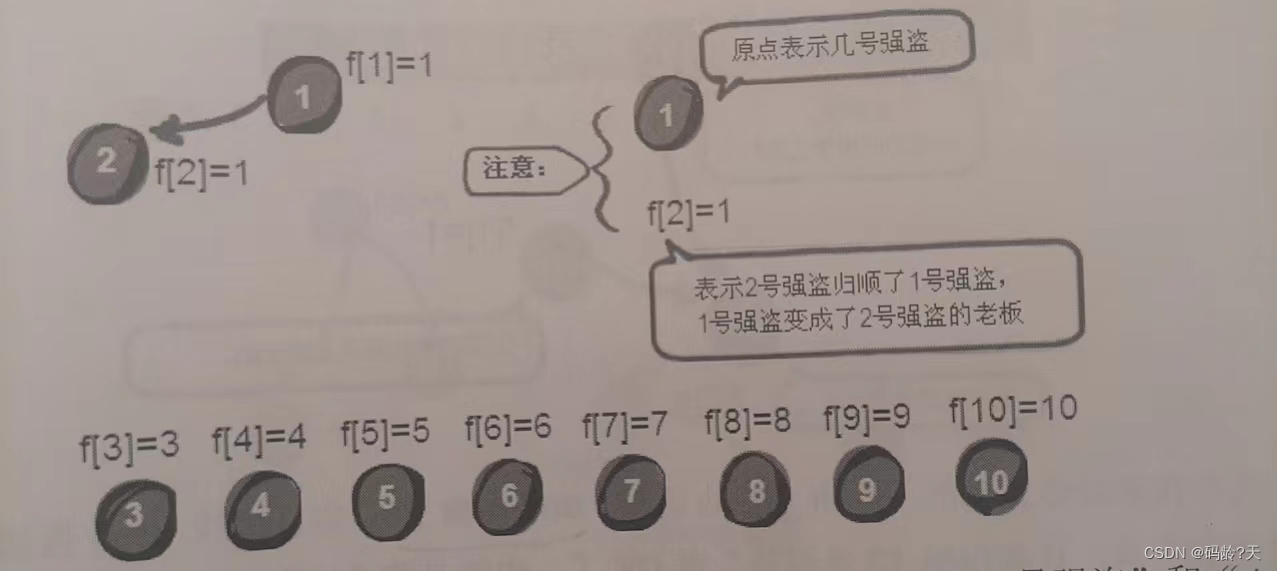
我们假定左边的强盗更厉害些,规定一个“靠左法则”,比如警察得到的第一条线索是,1号和2号同伙
(1)
所以1号在左边,更厉害,那么2号归顺1号,也就是1号是2号的头头,所以dad[2] = 1;表示2号强盗的头是1号强盗

(2)
第二条线索,3--4(3号强盗和4号是同伙),根据“左边的更厉害”,4号归顺3号,所以 dad[4] = 3;
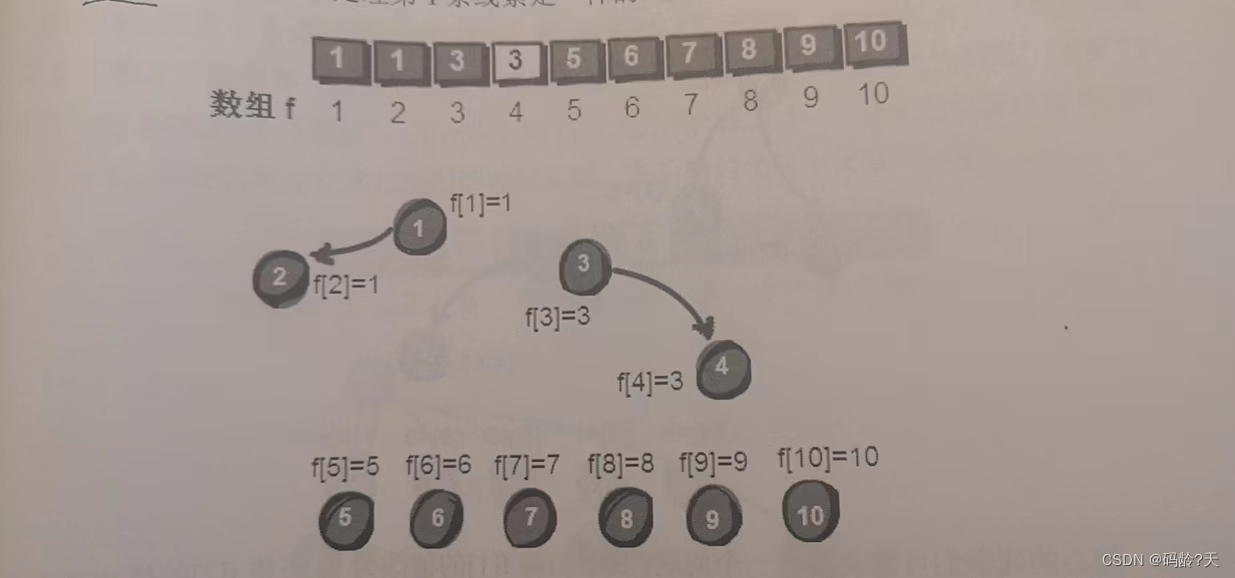
(3)
第3条线索,5--2,5号和2号强盗是同伙,dad[5] == 5,说明5号强盗的头是自己
dad[2] == 1,说明2号强盗的头是1号强盗
根据“左边的更厉害”,此时应该让2号归顺5号,那么“1号强盗”就不干了,“你凭什么抢我的人??”
于是这俩强盗差点打起来了,这让2号为难了,2号归顺5号还是继续跟着原来的头1号呢?
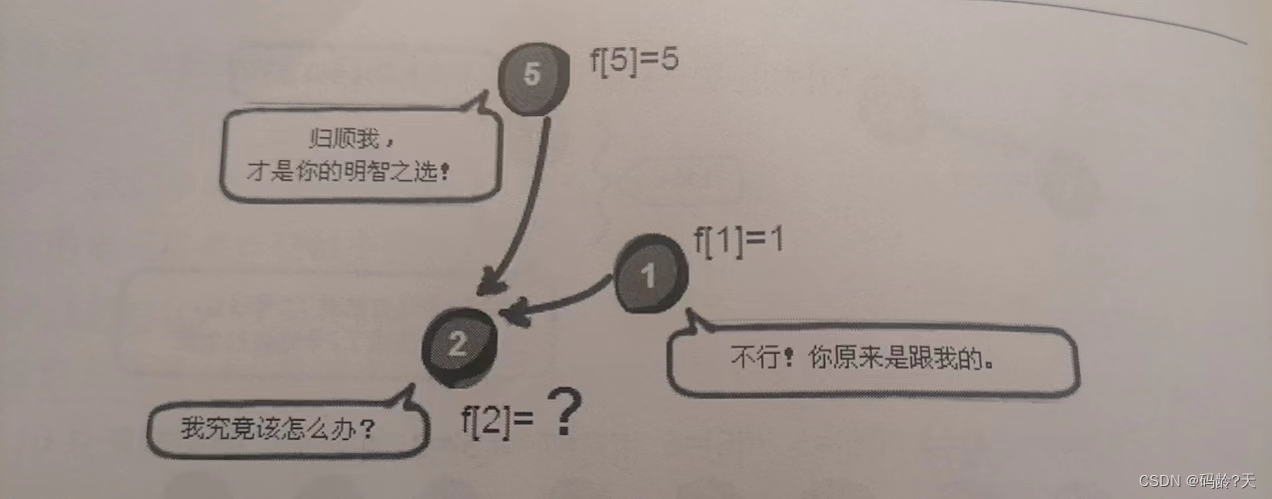
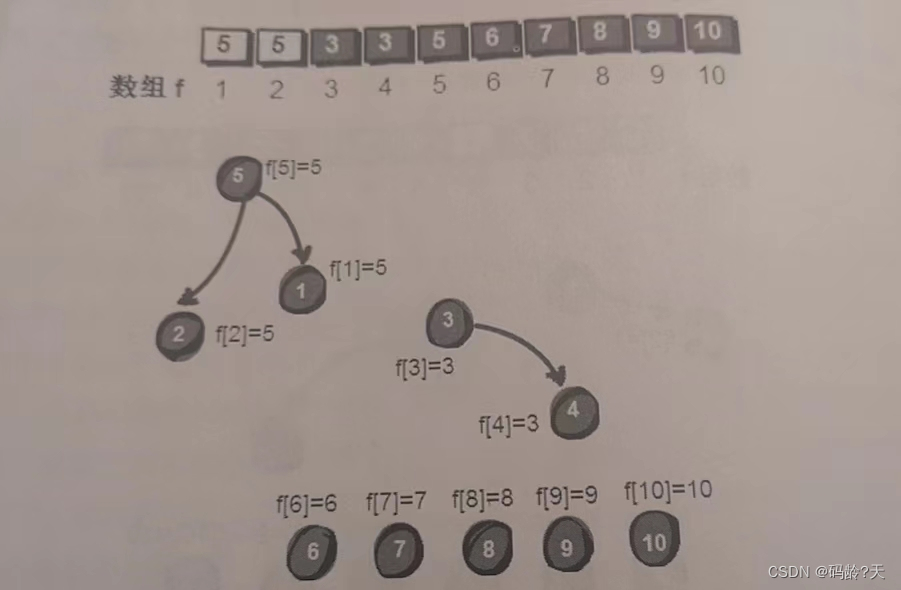
这里我们还是按左边的更厉害的原则,5号强盗直接找2号的头1号谈,让1号这个老大也归顺他(递归实现)
操作:dad[1] = 5; dad[2] = 5;
为什么在1号这个老大归顺5号后,还要再让2号归顺一次呢?
这一步不是必须的,但会提高后面找强盗最高领导人的速度(也就是找树的祖先的速度)
否则,很容易形成单支树结构(一长条。。。),极大浪费空间和时间
dad[2] = 5; 这看似多余的一步,也叫路径压缩(不要觉得名字很高大上,其实就是一行代码的事)
第四条线索
4--6(这俩同伙)
此时dad[4] == 3, dad[6] == 6,我们让6号强盗加入“3号犯罪团伙”,即dad[6] = 3;
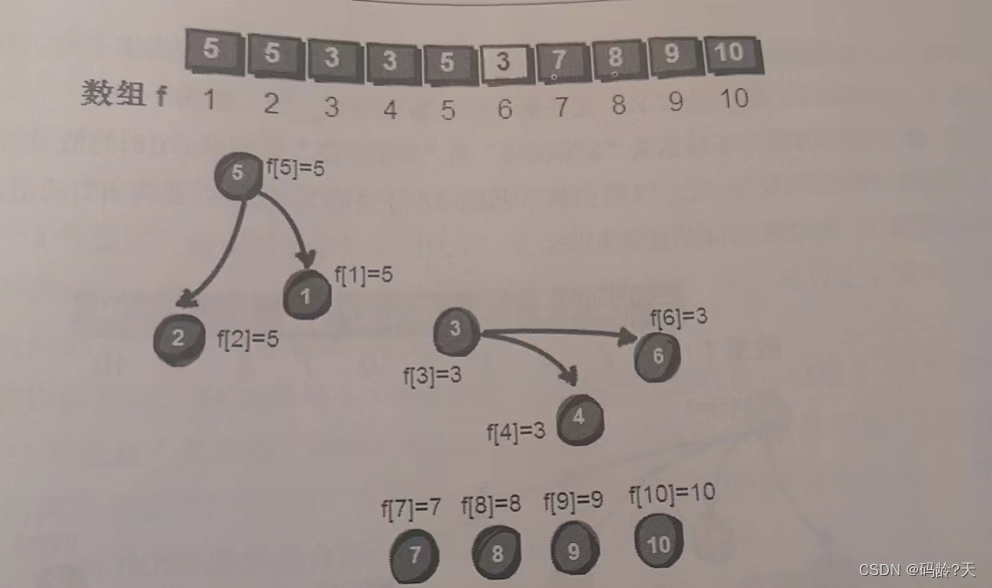
第5条线索
2--6
此时dad[2] == 5, dad[6] == 3
我们令6号和他的老大都归顺“5号犯罪团伙”(递归实现),dad[6] = 5; 以及 dad[3] = 5;
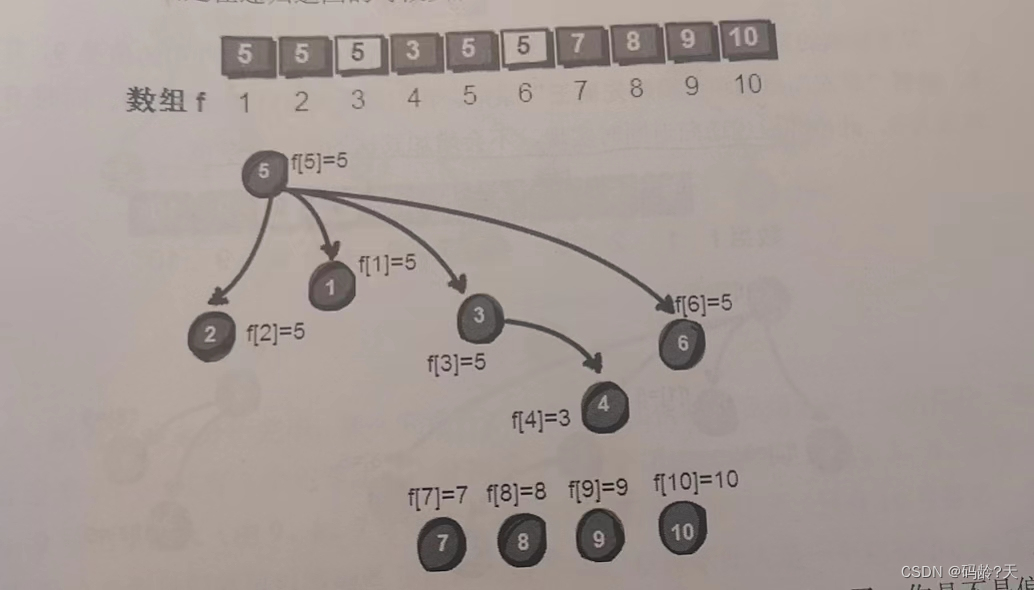
第6条线索
8--7
此时dad[8] == 8, dad[7] == 7, 让7号归顺8号好了,dad[7] = 8;

第7条线索
9--7
此时dad[9] == 9, dad[7] == 8,所以8号和7号都归顺9号强盗(路径压缩)(递归实现)
dad[8] = 9; dad[7] = 9;
除了让7号的老大归顺9号,我们还让7号也直接归顺9号,这一步叫路径压缩,这一步通过递归返回时实现,不会增加时间复杂度
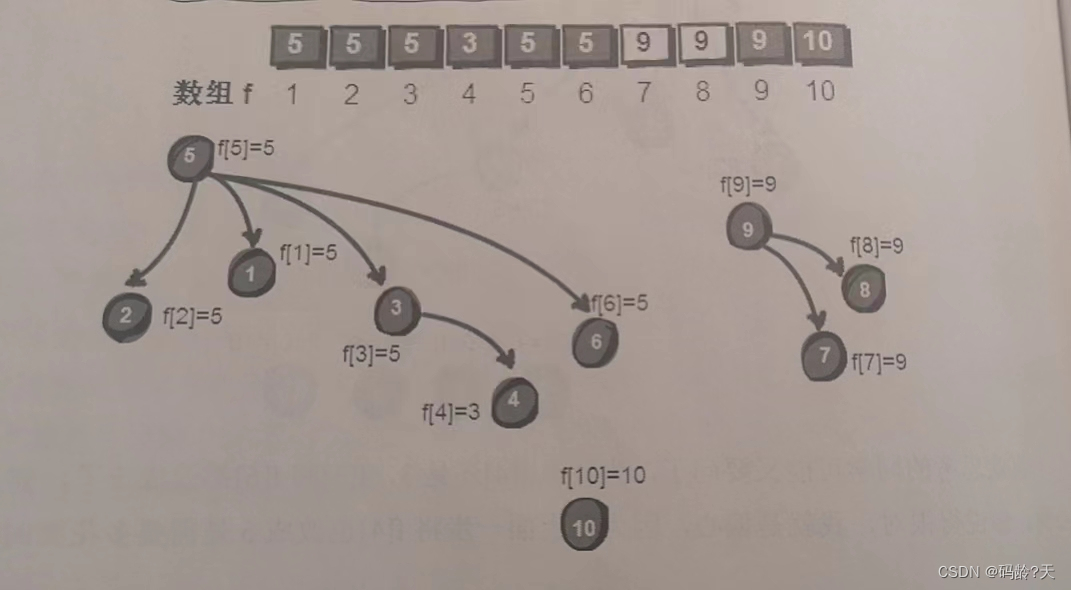
第8条线索
1--6
此时dad[1] == 5, dad[6] == 5,已经是同伙了,不需要操作
第9条线索
2--4
此时dad[2] == 5, dad[4] == 3
4号归顺3号,3号归顺5号,5号归顺自己,所以5号是最高领导人
从4号顺藤摸瓜到5号最高领导人的过程,就是递归
递归完后,dad[4] == 5;
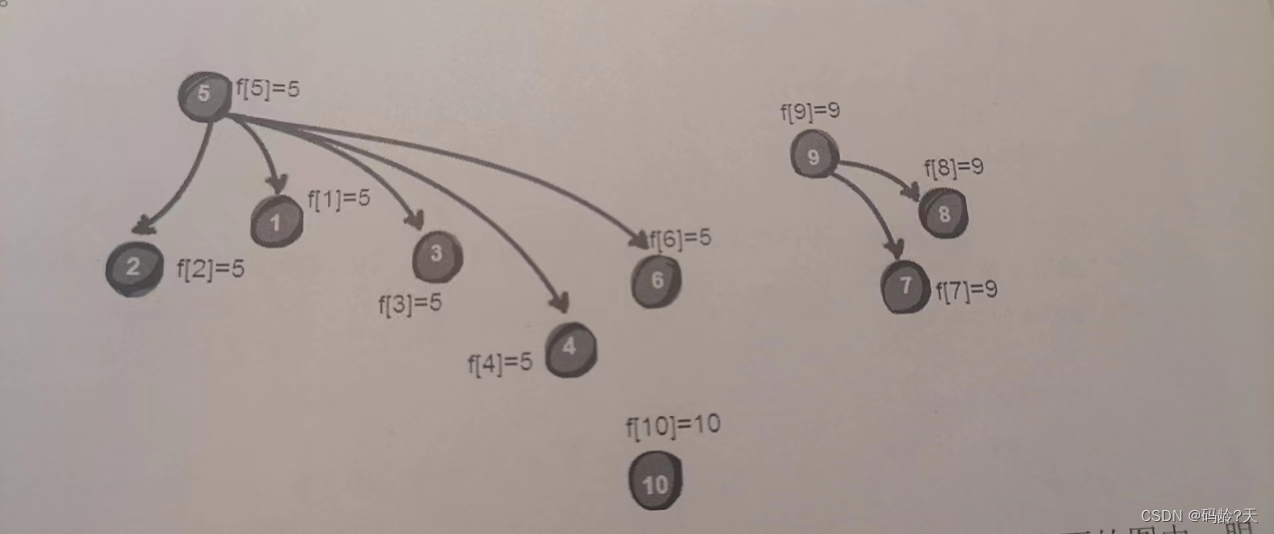
至此,所有线索分析完毕!那么有多少个犯罪团伙呢?
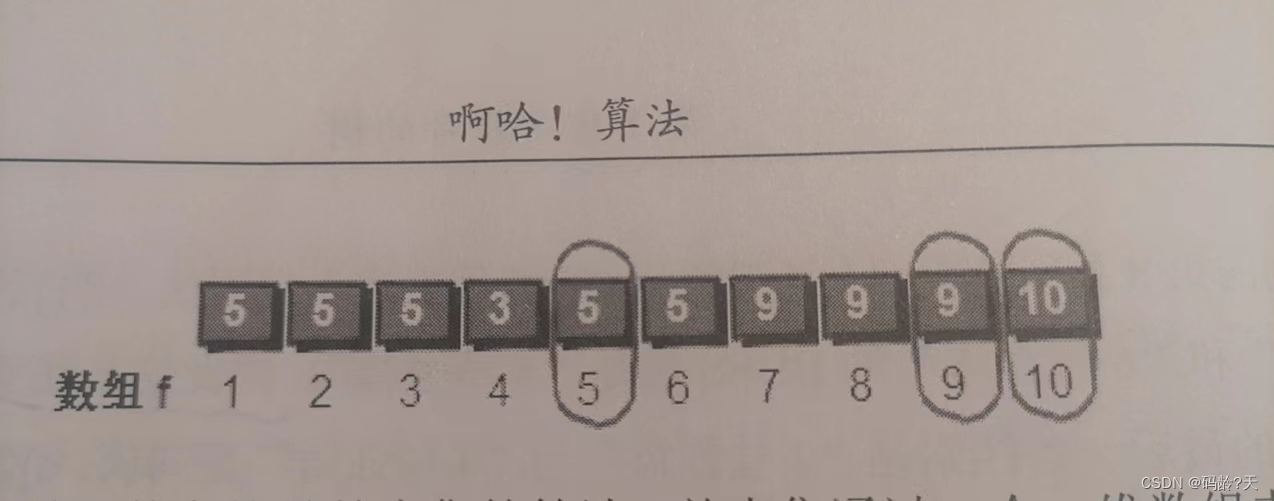
由上图可知,3个团伙
5号犯罪集团:5,2,1,3,4,6组成
9号犯罪集团:9,8,7组成
10号犯罪集团:10组成
容易知道,如果 dad[i] == i,表示 i 号强盗是一个团伙的最高领导人,最后数组dad中:
dad[5] == 5, dad[9] == 9, dad[10] == 10,所以共3个犯罪团伙
🌼总结
我们刚才模拟的是并查集算法,并查集通过一个一维数组实现,本质是维护一个森林。
初始,森林每个点都是孤立的,也就是每个强盗的老大都是自己,也可以理解为每个点就是一棵只有一个节点的树
之后,将这些孤立的点合并成一颗大树,合并的过程就是叫爸爸的过程
叫爸爸的过程,遵循“左边更厉害”和“擒贼先擒王”的原则
“擒贼先擒王”也就是,先让老大归顺左边的强盗,自己再归顺(自己再归顺就是路径压缩)
补充: 并查集也称为为不相交集数据结构
🌼代码
👊观察过程代码
#include<iostream>
using namespace std;
int dad[100];int Find(int x) //不停认老大, 直到顶头上司
{if(dad[x] == x) return x;else {//路径压缩, 将路径上所有点的上级都设置为根节点dad[x] = Find(dad[x]);return dad[x];}
}void join(int x, int y) //合并两个团伙
{//m为x的最高领导人, n为y的最高领导人int m = Find(dad[x]), n = Find(dad[y]);if(m != n) //路径压缩dad[n] = m; //第2个最高领导人认第1个当老大
}int main()
{for(int i = 1; i <= 10; ++i)dad[i] = i; //初始化自己为老大int a, b;for(int i = 1; i <= 9; ++i) {cout<<"第"<<i<<"条线索:";cin>>a>>b;join(a, b); //合并团伙cout<<dad[a]<<" "<<dad[b]<<endl;}int ans = 0;for(int i = 1; i <= 10; ++i)if(dad[i] == i)ans += 1;return 0;
}
第1条线索:1 2
1 1
第2条线索:3 4
3 3
第3条线索:5 2
5 1
第4条线索:4 6
3 3
第5条线索:2 6
1 3
第6条线索:8 7
8 8
第7条线索:9 7
9 8
第8条线索:1 6
5 3
第9条线索:2 4
1 3为什么第一次没实现路径压缩呢?(就是,虽然团伙总数确定了,但是每个人依然跟着自己原来的老大,没有跟着顶头上司)
原来是代码第18行
m = Find(dad[x]), n = Find(dad[y]);
应该改成
m = Find(x), n = Find(y);
否则只是令右老大归顺了左老大,但是右小弟没有直接归顺左老大,右小弟依然跟着右老大
这样就没起到路径压缩的效果
👊正确代码
即使是正确代码,《啊哈算法》里也存在BUG,不过无关痛痒而已(对时间复杂度几乎没影响)
#include<iostream>
using namespace std;
int dad[100];int Find(int x) //不停认老大, 直到顶头上司
{if(dad[x] == x) return x;else {//路径压缩, 将路径上所有点的上级都设置为根节点dad[x] = Find(dad[x]); //递归返回return dad[x];}
}void join(int x, int y) //合并两个团伙
{//m为x的最高领导人, n为y的最高领导人int m = Find(x), n = Find(y);if(m != n) //路径压缩dad[n] = m; //第2个最高领导人认第1个当老大
}int main()
{for(int i = 1; i <= 10; ++i)dad[i] = i; //初始化自己为老大int a, b;for(int i = 1; i <= 9; ++i) {cin>>a>>b;join(a, b); //合并团伙}int ans = 0;for(int i = 1; i <= 10; ++i)if(dad[i] == i)ans += 1;for(int i = 1; i <= 10; ++i)cout<<"第"<<i<<"个强盗的老大是"<<dad[i]<<endl;cout<<"共有"<<ans<<"个犯罪团伙";return 0;
}
1 2
3 4
5 2
4 6
2 6
8 7
9 7
1 6
2 4
第1个强盗的老大是5
第2个强盗的老大是5
第3个强盗的老大是5
第4个强盗的老大是5
第5个强盗的老大是5
第6个强盗的老大是5
第7个强盗的老大是8
第8个强盗的老大是9
第9个强盗的老大是9
第10个强盗的老大是10
共有3个犯罪团伙上述代码实现了路径压缩,但是第7个强盗的老大怎么还是8呢,不应该是9吗
因为这种较为简单的路径压缩,有一个小小的缺陷:
需要第一次先找到祖宗,第二次才能对路径上的节点进行压缩,而输入9 7前,7原来的老大是8,8的原来的老大也是8;当输入9 7后,进行join()函数
此时7的老大8号就归顺了9号,但7的老大依然是8号,没有变成9号,需要在下一次递归查找老大时,7的老大才变成9号,但此时已经没有下次了
当然,我们也可以在join()函数的最后重写一次 n = Find(y);
就可以实现书里的效果,但是不知道这样是否会影响时间复杂度
👊细节代码
#include<iostream>
using namespace std;
int dad[100];int Find(int x) //不停认老大, 直到顶头上司
{if(dad[x] == x) return x;else {//路径压缩, 将路径上所有点的上级都设置为根节点dad[x] = Find(dad[x]); //递归返回return dad[x];}
}void join(int x, int y) //合并两个团伙
{//m为x的最高领导人, n为y的最高领导人int m = Find(x), n = Find(y);if(m != n) //路径压缩dad[n] = m; //第2个最高领导人认第1个当老大n = Find(y); //重写一次
}int main()
{for(int i = 1; i <= 10; ++i)dad[i] = i; //初始化自己为老大int a, b;for(int i = 1; i <= 9; ++i) {cin>>a>>b;join(a, b); //合并团伙}int ans = 0;for(int i = 1; i <= 10; ++i)if(dad[i] == i)ans += 1;for(int i = 1; i <= 10; ++i)cout<<"第"<<i<<"个强盗的老大是"<<dad[i]<<endl;cout<<"共有"<<ans<<"个犯罪团伙";return 0;
}
1 2
3 4
5 2
4 6
2 6
8 7
9 7
1 6
2 4
第1个强盗的老大是5
第2个强盗的老大是5
第3个强盗的老大是5
第4个强盗的老大是5
第5个强盗的老大是5
第6个强盗的老大是5
第7个强盗的老大是9
第8个强盗的老大是9
第9个强盗的老大是9
第10个强盗的老大是10
共有3个犯罪团伙相关文章:

并查集(13张图解)--擒贼先擒王
目录 前言 故事 🌼思路 🌼总结 🌼代码 👊观察过程代码 👊正确代码 👊细节代码 来自《啊哈算法》 前言 刚学了树在优先队列中的应用--堆的实现 那么树还有哪些神奇的用法呢?我们从一…...
Flutter3引用原生播放器-IOS(Swift)篇
前言由于Flutter项目中需要使用到播放器功能,因此对flutter中各种播放器解决方案进行了一番研究和比对,最后决定还是自己通过Plugin的方法去引用原生播放器符合自己的需求,本篇文章会对各种解决方案做一个简单的比较,以及讲解一下…...
【蓝桥杯每日一题】双指针算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...
拼数(一般贪心)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题号:NC16783 时间限制:C/C 1秒,其他语言2秒 空间限制:C/C 262144K,其他语言524288K 64bit IO Format: %lld 题目描述 设有n个正整…...

LeetCode 热题 C++ 169. 多数元素 10. 正则表达式匹配 155. 最小栈
力扣169 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出࿱…...
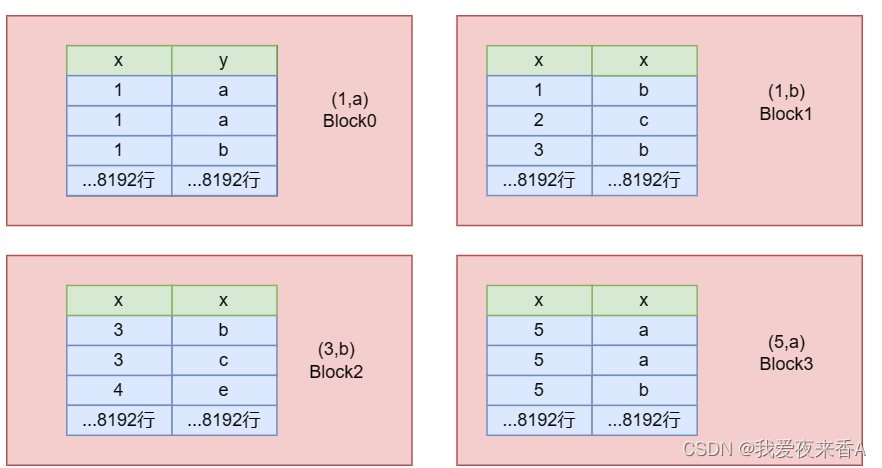
Clickhouse学习:MergeTree
MergeTree一、MergeTree逻辑存储结构二、MergeTree物理存储结构三、总结一、MergeTree逻辑存储结构 如上图所示,在排序键(CountrID、Date)上做索引,数据会按照这两个字段先后排序ClickHouse是稀疏索引,每隔8192行做一个索引,如(a,1),(a,2),比如想查a,要读取[0,3)之间的内容,稀疏…...
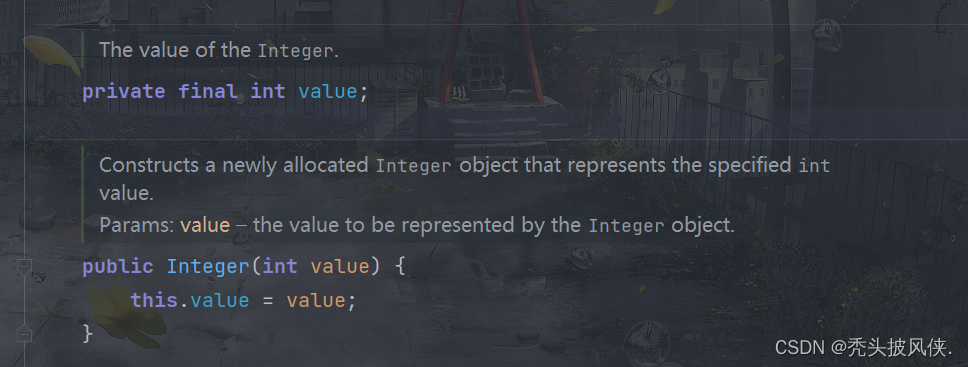
【java基础】包装类,自动装箱和自动拆箱
文章目录基本介绍包装类自动装箱自动拆箱包装类注意事项包装类比较包装器内容不可变基本介绍 有时,需要将int这样的基本类型转换为对象。所有的基本类型都有一个与之对应的类。 例如,Integer类对应基本类型int。通常,这些类称为包装器&#…...
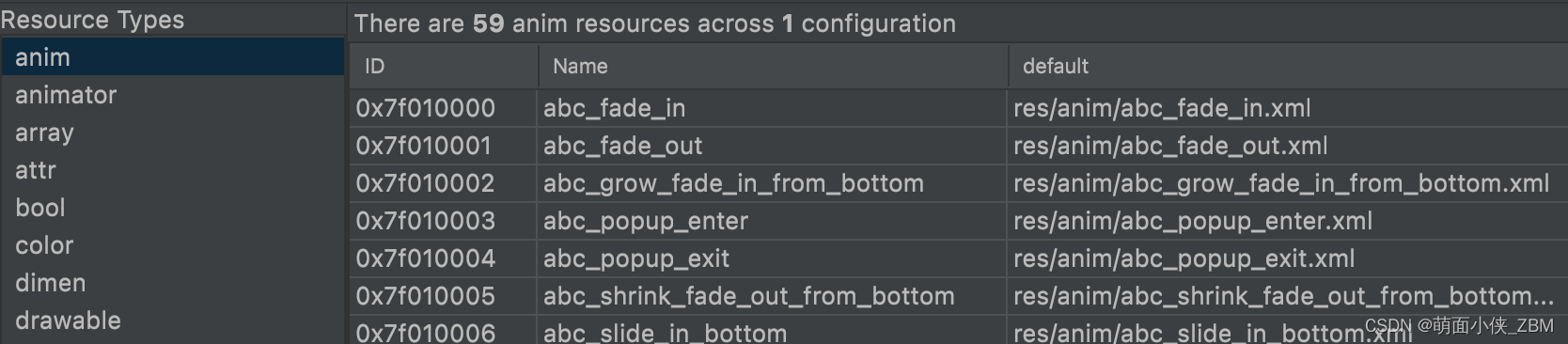
Android笔记(二十五):两种sdk热更插件资源加载方案
背景 在研究sdk插件化热更新方式的过程中总结出了两套插件资源加载方案,在此记录下 资源热更方式 方式一:合并所有插件资源 需要解决资源id冲突问题 资源ID值一共4个字段,由三部分组成:PackageIdTypeIdEntryId PackageId&…...

spring框架--全面详解(学习笔记)
目录 1.Spring是什么 2.Spring 框架特点 3.Spring体系结构 4.Spring开发环境搭建 5.spring中IOC和DI 6.Spring中bean的生命周期 7.Spring Bean作用域 8.spring注解开发 9.Spring框架中AOP(Aspect Oriented Programming) 10.AOP 实现分类 11.A…...
)
2023年CDGA考试模拟题库(401-500)
2023年CDGA考试模拟题库(401-500) 401.数据管理战略的SMART原则指的是哪项? [1分] A.具体 、高质量、可操作 、现实、有时间限制 B.具体、可衡量、可检验、现实、有时间限制 C.具体、可衡量、可操作、现实、有时间限制 D.具体、高质量、可检验、现实12-24个月的目标 答…...

软件设计师备考文档
cpu 计算机的基本硬件系统:运算器、控制器、存储器、输入设备、输出设备 cpu负责获取程序指令,对指令进行译码并加以执行 * cpu的功能控制器(保证程序正常执行,处理异常事件) 程序控制操作控制运算器(只能…...
)
Javascript的API基本内容(一)
一、获取DOM对象 querySelector 满足条件的第一个元素 querySelectorAll 满足条件的元素集合 返回伪数组 document.getElementById 专门获取元素类型节点,根据标签的 id 属性查找 二、操作元素内容 通过修改 DOM 的文本内容,动态改变网页的内容。 inn…...

10、最小公倍数
法一: #include <stdio.h>int main(){int a,b;scanf("%d%d",&a,&b);int m a>b?a:b;//m表示a,b之间的较大值while(1){if(m%a0&&m%b0){break;}m;}printf("%d",m);return 0; }法二:a*i%b0成立 #include &…...

【vue】vue2.x项目中使用md文件
一、Vue项目展示md文件的三种方式 1、将md文件 导入为 html 生成的标题标签自带具有id属性,值为标题内容; <h2 id"测试">测试</h2> # 处理md为html字符串 yarn add markdown-loader # 处理字符串,用于导出显示 yarn a…...

操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 注:阅读本编文章前,请先阅读系列文章,以免造成看不懂的情况!! MSF和CS绕过UAC提权 CS绕过UAC提权 拿到一个普通管理员的SHELL,在CS中没有*号代表有…...

快速排序+快速定位
快速排序算法采用了分治法以及递归作为解决问题的思想。在计算机科学中,分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以…...

nginx http rewrite module 详解
大家好,我是 17。 今天和大家聊聊 nginx http rewrite module 。 简单来说, ngx_http_rewrite_module module 用正则匹配请求,改写请求,然后做跳转。可以是内部跳转,也可以是外部跳转。 学习这个模块的时候…...

机器学习可解释性一(LIME)
随着深度学习的发展,越来越多的模型诞生,并且在训练集和测试集上的表现甚至于高于人类,但是深度学习一直被认为是一个黑盒模型,我们通俗的认为,经过训练后,机器学习到了数据中的特征,进而可以正…...

CV学习笔记-MobileNet
MobileNet 文章目录MobileNet1. MobileNet概述2. 深度可分离卷积(depthwise separable convolution)2.1 深度可分离卷积通俗理解2.2 深度可分离卷积对于参数的优化3. MobileNet网络结构4. 代码实现4.1 卷积块4.2 深度可分离卷积块4.3 MobileNet定义4.4 完…...

C++进阶——继承
C进阶——继承 1.继承的概念及定义 面向对象三大特性:封装、继承、多态。 概念: 继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段,它允许程序员在保持原有类特 性的基础上进行扩展,增加功能,这…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
