【OJ for Divide and Conquer】OJ题解
文章目录
- A - Ultra-QuickSort
- B - Hanoi Tower Troubles Again! [找规律+递归]
- C - Fibonacci Again[找规律]
- E - [Fire Net](https://programmerall.com/article/7276104269/)[DFS 搜索 ⭐⭐]
- F - Gridland[找规律]
- G - Maximum Subarray Sum[动态规划/分治..经典⭐]
- I - Quoit Design[最近点对距离]
A - Ultra-QuickSort
In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence
9 1 0 5 4 ,
Ultra-QuickSort produces the output
0 1 4 5 9 .
Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.
简单来说,就是有一组无序的数组,求两两交换的最小次数使得数组升序排列。
分析:要使得数组升序排列,
here 🙋 查看归并算法总结
我们只需要在归并排序的算法中,在合并时,判断前面子数列的值是否大于后面子序列的值。
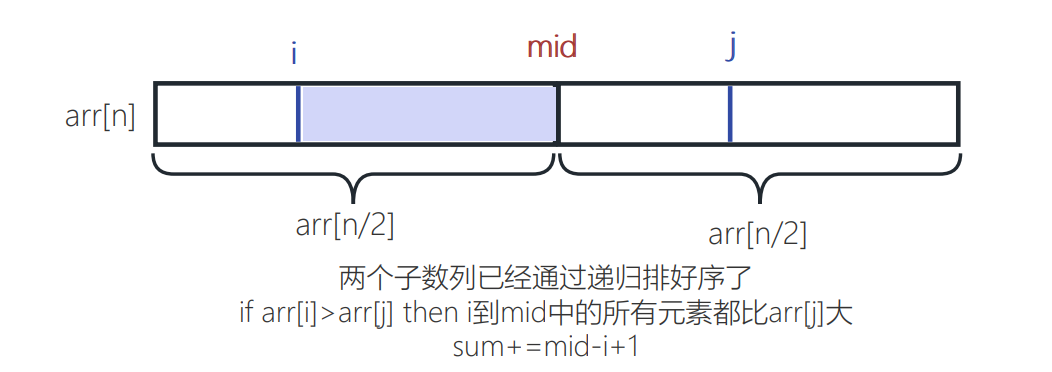
注意一个易错点,每轮loop都必须要指定退出条件,在这里条件就是当两个子序列的指针指向同一个数时,退出。
if(l>=r) return;
整体代码如下,
#include<iostream>
#include<vector>
using namespace std;
int arr[500010];
int tmp[500010];
int sum=0;
//归并算法
void mergesort(int l,int r){if(l>=r) return;int mid=(l+r)/2;mergesort(l,mid);mergesort(mid+1,r);int i=l,j=mid+1,k=l;while(i<=mid && j<=r){// cout<<"f"; while(arr[i]<=arr[j] && i<=mid) tmp[k++]=arr[i++];while(arr[i]>arr[j] && j<=r) {tmp[k++]=arr[j++];sum+=mid+1-i;}}while(i<=mid) tmp[k++]=arr[i++];while(j<=r) tmp[k++]=arr[j++];for(int k=l;k<=r;k++)arr[k]=tmp[k];
}
int main(){int n;while(cin>>n && n){for(int i=0;i<n;i++){cin>>arr[i];}sum=0;mergesort(0,n-1);cout << sum << endl;}
}
B - Hanoi Tower Troubles Again! [找规律+递归]
People stopped moving discs from peg to peg after they know the number of steps needed to complete the entire task. But on the other hand, they didn’t not stopped thinking about similar puzzles with the Hanoi Tower. Mr.S invented a little game on it. The game consists of N pegs and a LOT of balls. The balls are numbered 1,2,3… The balls look ordinary, but they are actually magic. If the sum of the numbers on two balls is NOT a square number, they will push each other with a great force when they’re too closed, so they can NEVER be put together touching each other.
The player should place one ball on the top of a peg at a time. He should first try ball 1, then ball 2, then ball 3… If he fails to do so, the game ends. Help the player to place as many balls as possible. You may take a look at the picture above, since it shows us a best result for 4 pegs.
简单来说,看每次提供的柱子数可以承载多少个圆盘,使得每根柱子上相邻两圆盘的加和必定为平方数。
分析:这道题看起来很难,实际上从简单情况入手。先看一根柱子、再看两根柱子…发现能承载圆盘的数量依次为1、3、7、11、17、23,每两个之间相差2、4、4、6、6…于是我们发现了规律。实际上,用数学方法证明也能得出该结论。
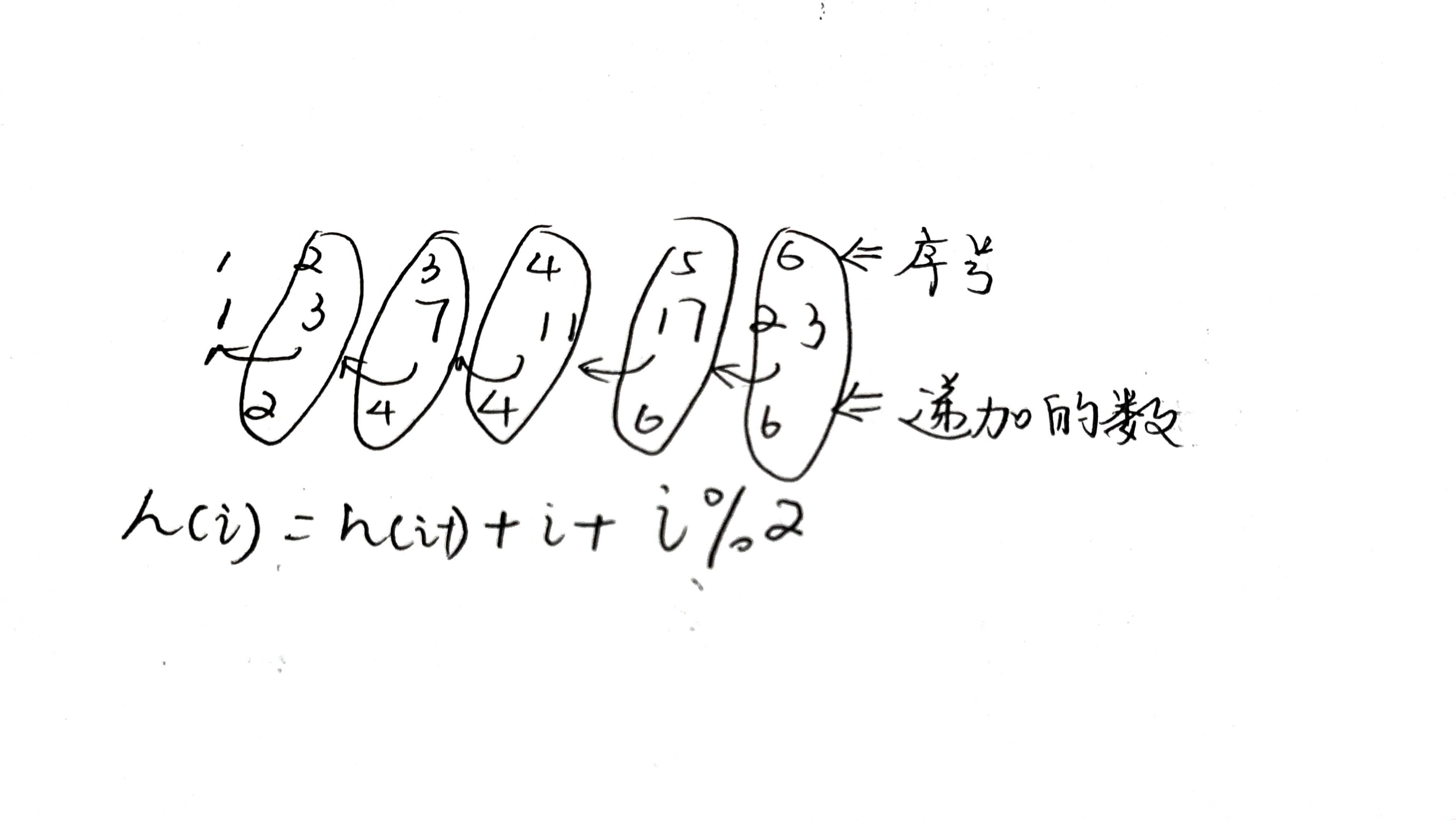
递推公式: H a n o i ( i ) = H a n o i ( i − 1 ) + i + i % 2 Hanoi(i)=Hanoi(i-1)+i+i \% 2 Hanoi(i)=Hanoi(i−1)+i+i%2
考虑到题目中有多次求解,所以我们用表格的方式将结果先提前算好存储起来。
void Hanoi(){table[1]=1;table[2]=3;for(int i=3;i<N;i++)table[i]=table[i-1]+i+i%2;
}
全部代码也就很明晰了:
#include<iostream>
using namespace std;
#define N 55
int table[N];
//打表过程 避免重复计算
void Hanoi(){table[1]=1;table[2]=3;for(int i=3;i<N;i++)table[i]=table[i-1]+i+i%2;
}
int main(){int n,x;cin>>n;Hanoi();for(int i=0;i<n;i++){cin>>x;cout<<table[x]<<endl;}
}
补充:
- 宏定义格式
#define 宏名 替换文本
#define N 10; // 宏定义
int c[N]; // 会被替换为: int c[10;];
C - Fibonacci Again[找规律]
There are another kind of Fibonacci numbers: F(0) = 7, F(1) = 11, F(n) = F(n-1) + F(n-2) (n>=2)
Input
Input consists of a sequence of lines, each containing an integer n. (n < 1,000,000)
Output
Print the word “yes” if 3 divide evenly into F(n).
Print the word “no” if not.
分析:注意 斐波那契数列会议非常快的速度增长,因此直接计算出结果并和3运算取余的做法不可取。我们考虑列出前面部分结果,试图找规律。嘿,还真成功了!
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 11 | 18 | 29 | 47 | 76 | 123 | 199 | 322 | 521 | 843 |
| √ | √ | √ |
观察表格:发现每4个为一组。在数组的第3个数时,可以被整除,也就是输出yes.
int main(){int n;int f[4]={0,0,1,0};while(cin>>n){if(f[n%4]) cout<<"yes"<<endl;else cout<<"no"<<endl;}
}
E - Fire Net[DFS 搜索 ⭐⭐]
Suppose that we have a square city with straight streets. A map of a city is a square board with n rows and n columns, each representing a street or a piece of wall.
A blockhouse is a small castle that has four openings through which to shoot. The four openings are facing North, East, South, and West, respectively. There will be one machine gun shooting through each opening.
Here we assume that a bullet is so powerful that it can run across any distance and destroy a blockhouse on its way. On the other hand, a wall is so strongly built that can stop the bullets.
The goal is to place as many blockhouses in a city as possible so that no two can destroy each other. A configuration of blockhouses is legal provided that no two blockhouses are on the same horizontal row or vertical column in a map unless there is at least one wall separating them. In this problem we will consider small square cities (at most 4x4) that contain walls through which bullets cannot run through.
The following image shows five pictures of the same board. The first picture is the empty board, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this board, the maximum number of blockhouses in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways.
Your task is to write a program that, given a description of a map, calculates the maximum number of blockhouses that can be placed in the city in a legal configuration.
分析:
map中各个符号的意义:
| X | . | % |
|---|---|---|
| 有墙(可以避开💣) | 啥也没有 | 有碉堡(可以四处散布💣) |
采用DFS的思想
深度优先搜索的步骤分为
1.递归下去 2.回溯上来。
顾名思义,深度优先,则是以深度为准则,先一条路走到底,直到达到目标。这里称之为递归下去。否则既没有达到目标又无路可走了,那么则退回到上一步的状态,走其他路。这便是回溯上来。总结DFS模板:【注意恢复现场这一步】
这道题的IDEA:
从左上角的元素开始进行深度搜索,一直搜索到右下角位置。使用check检查函数判断当前搜索到的位置能不能放置碉堡,若是可以放置,则将本轮的总和加一,并将此处标记为%,意思是有一座碉堡。然后继续进行深度搜索。如果已经到了最右下角位置,则回溯并记录最大值。
#include<iostream>
#include<algorithm>
using namespace std;
int n,ans=0;
char arr[5][5];int check(int x,int y){for(int i=x-1;i>=0;i--){if(arr[i][y]=='%') return false;if(arr[i][y]=='X') break;}for(int i=x+1;i<n;i++){if(arr[i][y]=='%') return false;if(arr[i][y]=='X') break;}for(int i=y-1;i>=0;i--){if(arr[x][i]=='%') return false;if(arr[x][i]=='X') break;}for(int i=x+1;i<n;i++){if(arr[x][i]=='%') return false;if(arr[x][i]=='X') break;}return true;
}//s表示当前的状态吧
void dfs(int s,int sum){if(s==n*n){ans=max(ans,sum);return;}int x=s/n;int y=s%n;if(arr[x][y]=='.' && check(x,y)){arr[x][y]='%'; //表示成功加入一个碉堡dfs(s+1,sum+1); //继续深度搜索arr[x][y]='.'; //!还原标记!}dfs(s+1,sum);
}int main(){while(cin>>n && n){ans=0;for(int i=0;i<n;i++)cin>>arr[i]; dfs(0,0);cout<<ans<<endl;}
}
F - Gridland[找规律]
For years, computer scientists have been trying to find efficient solutions to different computing problems. For some of them efficient algorithms are already available, these are the “easy” problems like sorting, evaluating a polynomial or finding the shortest path in a graph. For the “hard” ones only exponential-time algorithms are known. The traveling-salesman problem belongs to this latter group. Given a set of N towns and roads between these towns, the problem is to compute the shortest path allowing a salesman to visit each of the towns once and only once and return to the starting point.
The president of Gridland has hired you to design a program that calculates the length of the shortest traveling-salesman tour for the towns in the country. In Gridland, there is one town at each of the points of a rectangular grid. Roads run from every town in the directions North, Northwest, West, Southwest, South, Southeast, East, and Northeast, provided that there is a neighbouring town in that direction. The distance between neighbouring towns in directions North–South or East–West is 1 unit. The length of the roads is measured by the Euclidean distance. For example, Figure 7 shows 2 × 3-Gridland, i.e., a rectangular grid of dimensions 2 by 3. In 2 × 3-Gridland, the shortest tour has length 6.
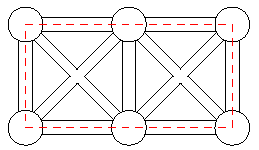
分析:初一看很难,但只要从简单情况出发,找寻规律,就可得到意外之喜😊
只要多做几组你就会发现规律:只要n,m有一个为偶数,答案为n*m;都为基数,答案为n*m-1+sqrt(2)
下图是当时很潦草的草稿…浅浅看一下吧❤
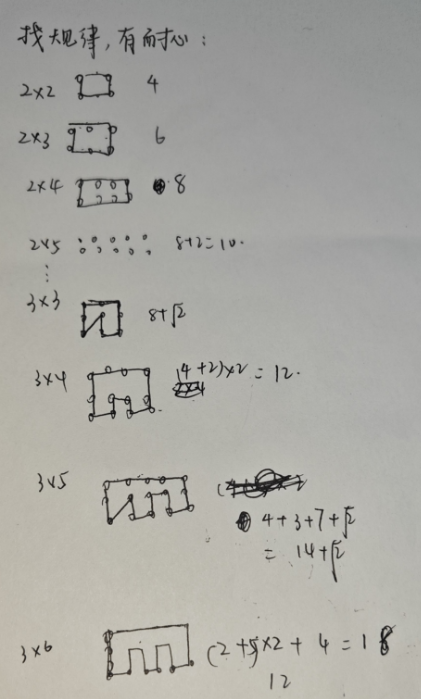
#include<iostream>
#include<math.h>using namespace std;int main(){int N;double ans;cin>>N;for(int i=1;i<=N;i++){int n,m;cin>>m>>n;if((m*n)%2) ans=m*n*1.0-1+sqrt(2);else ans=m*n*1.0;cout<<"Scenario #"<<i<<":\n";printf("%.2f\n\n",ans);}
}
补充一个知识点:
- prinf输出浮点数
>% - 0 m.n 格式字符
下面对组成格式说明的各项加以说明:
①%:表示格式说明的起始符号,不可缺少。
②-:有-表示左对齐输出,如省略表示右对齐输出。
③0:有0表示指定空位填0,如省略表示指定空位不填。
④m.n:m指域宽,即对应的输出项在输出设备上所占的字符数。N指精度。用于说明输出的实型数的小数位数。为指定n时,隐含的精度为n=6位。
G - Maximum Subarray Sum[动态规划/分治…经典⭐]
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
寻找和最大的子序列,并返回最大值
分析:
刚拿到这道题就想到了用动态规划的方法做。在每一步,我们维护两个变量,一个是全局最优,就是到当前元素为止最优的解是,一个是局部最优,就是必须包含当前元素的最优的解。其中这个局部最优,要么是从这个元素开始的新序列,要么是包含上一个元素的序列。
dp[i]=max(dp[i-1]+arr[i],arr[i]) dp是维护的局部最优解,arr是输入的数组。
#include<iostream>
#include<algorithm>
#include<climits>
using namespace std;
#define N 200100
int main(){int dp[N];int arr[N];int ans=INT_MIN;//INT_MIN:-2147483648 || INT_MAX:2147483647int n;cin>>n;for(int i=0;i<n;i++)cin>>arr[i];dp[0]=arr[0];for(int i=1;i<n;i++){dp[i]=max(dp[i-1]+arr[i],arr[i]);ans=max(ans,dp[i]);}cout<<ans<<endl;}
注意这道题目易错点是数组大小的开辟,小心审题就是了。
- 做题时候遇到了:runtime error (运行时错误)就是程序运行到一半,程序就崩溃了。可能有以下几种情况:
①除以零
②数组越界:int a[3]; a[10000000]=10;
③指针越界:int * p; p=(int *)malloc(5 * sizeof(int)); *(p+1000000)=10;
④使用已经释放的空间:int * p; p=(int *)malloc(5 * sizeof(int));free§; *p=10;
⑤数组开得太大,超出了栈的范围,造成栈溢出:int a[100000000];
I - Quoit Design[最近点对距离]
Have you ever played quoit in a playground? Quoit is a game in which flat rings are pitched at some toys, with all the toys encircled awarded.
In the field of Cyberground, the position of each toy is fixed, and the ring is carefully designed so it can only encircle one toy at a time. On the other hand, to make the game look more attractive, the ring is designed to have the largest radius. Given a configuration of the field, you are supposed to find the radius of such a ring.
Assume that all the toys are points on a plane. A point is encircled by the ring if the distance between the point and the center of the ring is strictly less than the radius of the ring. If two toys are placed at the same point, the radius of the ring is considered to be 0.
Input
The input consists of several test cases. For each case, the first line contains an integer N (2 <= N <= 100,000), the total number of toys in the field. Then N lines follow, each contains a pair of (x, y) which are the coordinates of a toy. The input is terminated by N = 0.
Output
For each test case, print in one line the radius of the ring required by the Cyberground manager, accurate up to 2 decimal places.
分析:这道题的难点在于读懂题!想要最大的圈直径,使得圈只能套到一个物品。其实就是找最近的两个点,之间的距离就是目标圈的直径。那么就变成了最近点对问题。链接 这个链接展示了详细的求解过程,可以仔细研究。
仔细看
相关文章:

【OJ for Divide and Conquer】OJ题解
文章目录 A - Ultra-QuickSortB - Hanoi Tower Troubles Again! [找规律递归]C - Fibonacci Again[找规律]E - [Fire Net](https://programmerall.com/article/7276104269/)[DFS 搜索 ⭐⭐]F - Gridland[找规律]G - Maximum Subarray Sum[动态规划/分治..经典⭐]I - Quoit Desi…...

使用 Sealos 一键部署 Kubernetes 集群
Sealos 是一款以 Kubernetes 为内核的云操作系统发行版,使用户能够像使用个人电脑一样简单地使用云。 与此同时,Sealos 还提供一套强大的工具,可以便利地管理整个 Kubernetes 集群的生命周期。 Sealos 不仅可以一键安装一个单节点的 Kubern…...

解读电力系统中的GPS北斗卫星同步时钟系统
随着电力系统的快速发展,变电站中的各类系统 :计算机监控系统、水情测报系统、视频监控系统 状态监测系统 生产信息管理系统等,各类装置:继电保护装置、故障录波装置、PMU装置、事件顺序记录SOE功能越来越强大,需要采集、记录的数…...

原子类:Java并发编程的利器
在多线程环境下,确保数据的一致性和原子性是至关重要的。Java提供了一些原子类,用于解决多线程并发问题。这些原子类能够确保操作在多线程环境下是原子的,即不会被其他线程干扰。本文将介绍Java中的原子类及其应用。 一、原子类概述 原子类…...

99%网工都会遇到的经典面试问题
①问题:介绍TCP连接的三次握手?追问:为什么TCP需要握手三次? 三次握手: 第一步:A向B发送一个SYN报文表示希望建立连接 第二步:B收到A发过来的数据包后,通过SYN得知这是一个建立连接的请求,于是发送ACK确认,由于TCP的全双工模式ÿ…...

html和css中图片加载与渲染的规则是什么?
浏览器渲染web页面的过程 解析html,构成dom树 2.加载css,构成样式规则树 3.加载js,解析js代码 4.dom树和样式树进行匹配,构成渲染树 5.计算元素位置进行页面布局 5.绘制页面,呈现到浏览器中 图片加载和渲染的过程 1.解…...

YOLO轻量化改进 , 边缘GPU友好的YOLO改进算法!
在本文中,作者根据现有先进方法中各种特征尺度之间缺少的组合连接的问题,提出了一种新的边缘GPU友好模块,用于多尺度特征交互。此外,作者提出了一种新的迁移学习backbone采用的灵感是来自不同任务的转换信息流的变化,旨…...

第15届蓝桥杯Scratch选拔赛中级(STEMA)真题2023年8月
第15届蓝桥杯Scratch选拔赛中级(STEMA)真题2023年8月 一、单选题 第 1 题 单选题 点击以下积木块,生成的随机数是一个( )。 A.整数 B.小数 C.整数或小数 D.以上都不对 第 2 题 单选题 运行以下程序࿰…...

c++二叉树遍历
参考文献 数据结构c语言版,严蔚敏_吴伟民著。 二叉树 中序遍历代码实现 #include<vector> #include<iostream> using namespace std;//Definition for a binary tree node. struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : v…...

day14_集合
今日内容 零、 复习昨日 一、集合框架体系 二、Collection 三、泛型 四、迭代 五、List(ArrayList、LinkedList) 零、 复习 throw和throws什么区别 throwthrows位置方法里面方法签名上怎么写throw 异常对象throws异常类名(多个)作用真正抛出异常对象声明抛出的异常类型 运行时…...

私有云:架构图
私有云:架构图 1、架构图2、服务器分配及配置3、本地物理机hosts文件配置4、相关软件包5、本地物理机电脑配置参考【内存最好20G往上】 机缘巧合之下突然想玩玩虚拟化,然后就查资料本地自己搭建一套私有云 使用【VMware Workstation】这个虚拟化软件来进…...

在安装和配置DVWA渗透测试环境遇到的报错问题
安装环境 前面的安装我参考的这个博主:渗透测试漏洞平台DVWA环境安装搭建及初级SQL注入-CSDN博客 修改bug 1.首先十分感谢提供帮助的博主,搭建DVWA Web渗透测试靶场_dvwa 白屏-CSDN博客,解决了我大多数问题,报错如下࿱…...
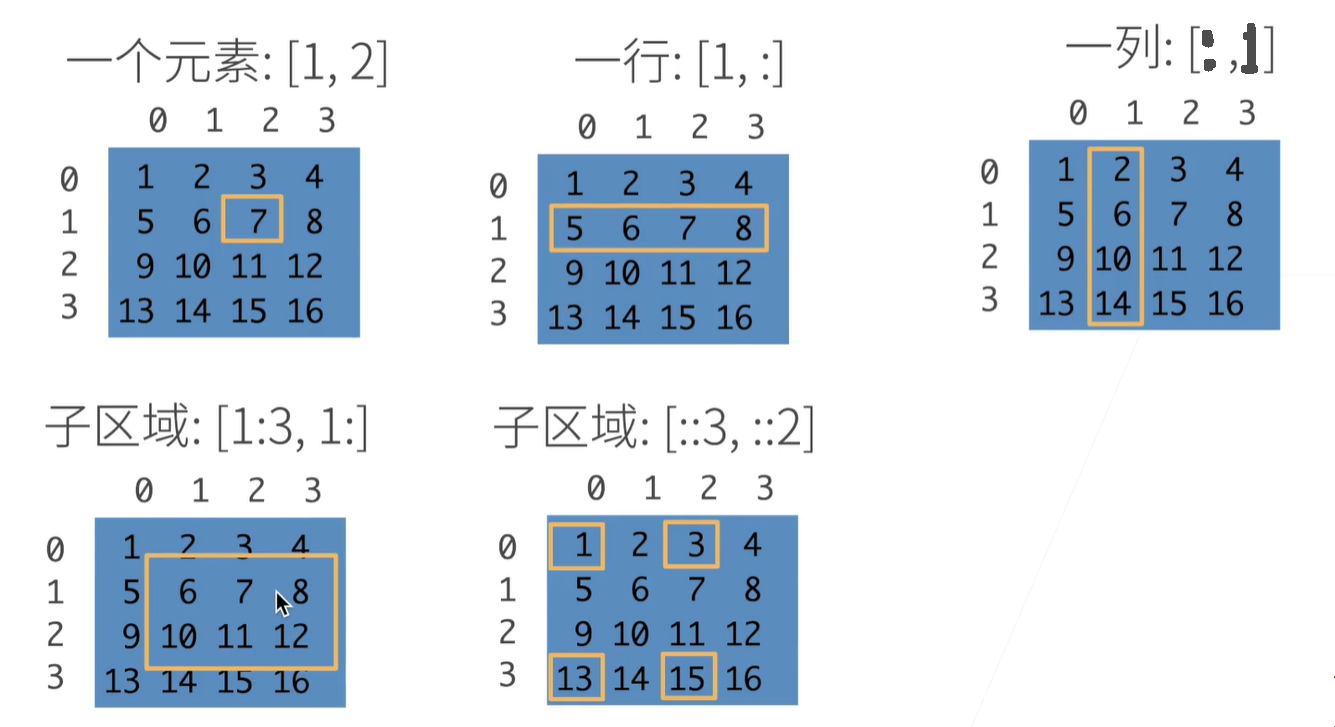
深度学习_2 数据操作
数据操作 机器学习包括的核心组件有: 可以用来学习的数据(data);如何转换数据的模型(model);一个目标函数(objective function),用来量化模型的有效性&…...
win 下安装 nvm 的使用与配置
nvm 全名 node.js version management,是一个 nodejs 的版本管理工具。通过它可以安装和切换不同版本的 nodejs。 注:如果已经安装了 nodejs 需先卸载后再安装 nvm 为了确保 nodejs 已彻底删除,可以看看安装目录中是否有 node 文件夹&#x…...

Git笔记
删除最后一次提交 git reset --hard HEAD~1...

省钱兄共享茶室共享娱乐室小程序都有哪些功能
随着共享经济的兴起,共享茶室和共享娱乐室作为一种新型的共享空间,逐渐受到了年轻人的青睐。省钱兄共享茶室共享娱乐室小程序作为该领域的优秀代表,集多种功能于一身,为用户提供了一个便捷、舒适、高效的社交娱乐平台。本文将详细…...

vue-cli方式创建vue3工程
创建工程前,可先用命令行查看是否安装vue-cli。 通过命令行查看vue-cli版本 vue --version 如果已安装vue-cli,则会显示当前安装版本 vue/cli 4.5.13 如果没有安装vue-cli,会提示安装 vue : 无法识别“vue”命令 需要通过npm全局安装v…...

四、W5100S/W5500+RP2040树莓派Pico<TCP Server数据回环测试>
文章目录 1. 前言2. 协议简介2.1 简述2.2 优点2.3 应用 3. WIZnet以太网芯片4. TCP Server数据回环测试4.1 程序流程图4.2 测试准备4.3 连接方式4.4 相关代码4.5 测试现象 5. 注意事项6. 相关链接 1. 前言 在计算机网络中,TCP Server是不可或缺的角色,它…...

技术视角下的跑腿小程序开发:关键挑战和解决方案
跑腿小程序作为连接服务提供者和用户的桥梁,面临着诸多技术挑战。本文将聚焦于技术层面的关键挑战,并提供解决方案,以帮助开发者应对技术上的复杂问题。 1. 实时性与性能挑战 挑战: 跑腿小程序需要实时地匹配订单、更新状态和提…...
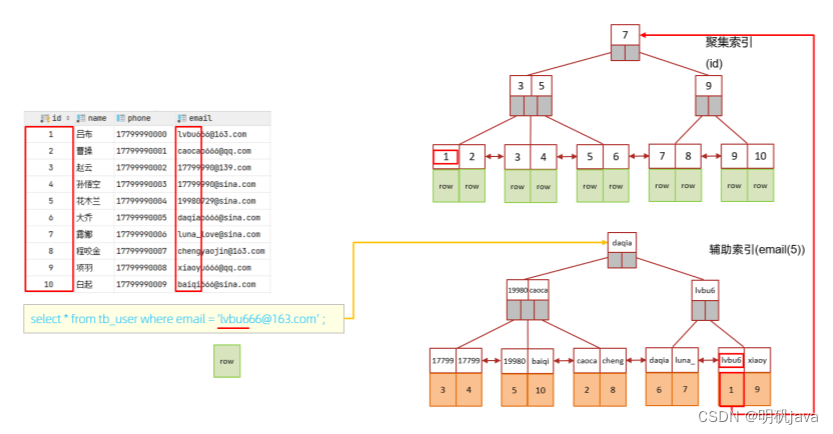
Mysql进阶-索引篇(下)
SQL性能分析 SQL执行频率 MySQL 客户端连接成功后,通过 show [session|global] status 命令可以提供服务器状态信息。通过如下指令,可以查看当前数据库的INSERT、UPDATE、DELETE、SELECT的访问频次,通过sql语句的访问频次,我们可…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

