【考研数学】概率论与数理统计 —— 第七章 | 参数估计(1,基本概念及点估计法)
文章目录
- 引言
- 一、参数估计的概念
- 二、参数的点估计
- 2.1 矩估计法
- 2.2 最大似然估计法
- 写在最后
引言
我们之前学了那么多分布,如正态分布 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2),泊松分布 P ( λ ) P(\lambda) P(λ) 等等,都是在已知 μ , σ , λ \mu,\sigma,\lambda μ,σ,λ 的情况下。那这些值是怎么来的呢?参数估计便可以帮助我们回答这一问题。
一、参数估计的概念
所谓参数估计,即总体 X X X 的分布已知,但其中分布中含有未知参数 θ \theta θ(或多个参数),从总体 X X X 中取简单随机样本 ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) ,且 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) (x1,x2,⋯,xn) 为样本观察值,利用样本对参数进行估计,称为参数估计。参数估计可分为点估计和区间估计。
二、参数的点估计
设总体 X X X 的分布已知,但其中分布中含有未知参数,从总体 X X X 中取简单随机样本 ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) ,且 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) (x1,x2,⋯,xn) 为其观察值。若用统计量 θ ^ ( X 1 , X 2 , ⋯ , X n ) \widehat{\theta}(X_1,X_2,\cdots,X_n) θ (X1,X2,⋯,Xn) 估计参数 θ \theta θ ,称其为参数 θ \theta θ 的估计量(本质上是一个随机变量),将样本观察值代入,称 θ ^ ( x 1 , x 2 , ⋯ , x n ) \widehat{\theta}(x_1,x_2,\cdots,x_n) θ (x1,x2,⋯,xn) 为参数 θ \theta θ 的估计值(本质上是一个常数)。
常见的点估计法有矩估计法和最大似然估计法。
2.1 矩估计法
1. 矩估计的基本思想
设总体为 X X X, ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) 为来自总体的简单随机样本,称
μ k = E ( X k ) ( k = 1 , 2 , ⋯ ) \mu_k=E(X^k)(k=1,2,\cdots) μk=E(Xk)(k=1,2,⋯) 为总体 X X X 的 k k k 阶原点矩;
A k = 1 n ∑ X i k ( k = 1 , 2 , ⋯ ) A_k=\frac{1}{n}\sum X_i^k(k=1,2,\cdots) Ak=n1∑Xik(k=1,2,⋯) 为样本的 k k k 阶原点矩,特别地, A 1 = X ‾ A_1=\overline{X} A1=X ;
B k = 1 n ∑ ( X i − X ‾ ) k ( k = 1 , 2 , ⋯ ) B_k=\frac{1}{n}\sum (X_i-\overline{X})^k(k=1,2,\cdots) Bk=n1∑(Xi−X)k(k=1,2,⋯) 为样本的 k k k 阶中心距。
矩估计法的依据就是大数定律,由独立同分布的大数定律,有 A k A_k Ak 依概率收敛于 μ k ( k = 1 , 2 , ⋯ ) . \mu_k(k=1,2,\cdots). μk(k=1,2,⋯).
2. 矩估计法的基本步骤
C a e s I : Caes\space I: Caes I: 含有一个参数 θ \theta θ
第一步,求 E ( X ) E(X) E(X) 或 E ( X 2 ) E(X^2) E(X2) ;
第二步,令 E ( X ) = X ‾ E(X)=\overline{X} E(X)=X 或 E ( X 2 ) = A 2 E(X^2)=A_2 E(X2)=A2 ,解出 θ \theta θ 的表达式,将观察值代入即得到估计值。
C a s e I I : Case\space II: Case II: 含有两个参数 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2
第一步,求 E ( X ) E(X) E(X), E ( X 2 ) E(X^2) E(X2) ;
第二步,令 E ( X ) = X ‾ , E ( X 2 ) = A 2 , D ( X ) = B 2 E(X)=\overline{X},E(X^2)=A_2,D(X)=B_2 E(X)=X,E(X2)=A2,D(X)=B2 ,解出 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2 的表达式,将观察值代入即得到估计值。
【例】设总体 X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma^2) X∼N(μ,σ2) , ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) 为来自总体的简单随机样本。(1)设 μ = 2 \mu=2 μ=2 ,求参数 σ 2 \sigma^2 σ2 的矩估计量;(2)设 μ \mu μ 未知,求参数 σ 2 \sigma^2 σ2 的矩估计量。
解:(1) E ( X ) = 2 , E ( X 2 ) = D ( X ) + [ E ( X ) ] 2 = σ 2 + 4 E(X)=2,E(X^2)=D(X)+[E(X)]^2=\sigma^2+4 E(X)=2,E(X2)=D(X)+[E(X)]2=σ2+4 。令 σ 2 + 4 = A 2 = 1 n ∑ X i 2 \sigma^2+4=A_2=\frac{1}{n}\sum X_i^2 σ2+4=A2=n1∑Xi2 得 σ ^ 2 = 1 n ∑ i = 1 n X i 2 − 4. \widehat{\sigma}^2=\frac{1}{n}\sum_{i=1}^nX_i^2-4. σ 2=n1i=1∑nXi2−4. (2) E ( X ) = μ , E ( X 2 ) = σ 2 + μ 2 E(X)=\mu,E(X^2)=\sigma^2+\mu^2 E(X)=μ,E(X2)=σ2+μ2 。令 E ( X ) = X ‾ , E ( X 2 ) = A 2 E(X)=\overline{X},E(X^2)=A_2 E(X)=X,E(X2)=A2 ,可计算得到矩估计量: σ ^ 2 = 1 n ∑ i = 1 n X i 2 − X ‾ 2 = 1 n ∑ i = 1 n ( X i − X ‾ ) 2 . \widehat{\sigma}^2=\frac{1}{n}\sum_{i=1}^nX_i^2-\overline{X}^2=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^2. σ 2=n1i=1∑nXi2−X2=n1i=1∑n(Xi−X)2. 对于第二问结果的变换,我们可以把 1 n ∑ i = 1 n ( X i − X ‾ ) 2 \frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^2 n1∑i=1n(Xi−X)2 拆开,写成 1 n ∑ i = 1 n ( X i 2 − 2 X i X ‾ + X ‾ 2 ) = 1 n ( ∑ i = 1 n X i 2 − 2 X ‾ ∑ i = 1 n X i + n X ‾ 2 ) = 1 n ∑ i = 1 n X i 2 − X ‾ 2 . \frac{1}{n}\sum_{i=1}^n(X_i^2-2X_i\overline{X}+\overline{X}^2)=\frac{1}{n}\bigg(\sum_{i=1}^nX_i^2-2\overline{X}\sum_{i=1}^nX_i+n\overline{X}^2\bigg)=\frac{1}{n}\sum_{i=1}^nX_i^2-\overline{X}^2. n1i=1∑n(Xi2−2XiX+X2)=n1(i=1∑nXi2−2Xi=1∑nXi+nX2)=n1i=1∑nXi2−X2.
2.2 最大似然估计法
设总体为 X X X, ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) 为来自总体的简单随机样本, ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) (x1,x2,⋯,xn) 为其观察值。样本 ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) 取 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) (x1,x2,⋯,xn) 的概率成为似然函数,记为 L ( θ ) L(\theta) L(θ) 或 L ( θ 1 , θ 2 ) L(\theta_1,\theta_2) L(θ1,θ2) 。
C a s e I : \pmb{Case\space I:} Case I: 总体 X X X 为离散型(分布律已知,但未知参数)
第一步:似然函数
L = P { X 1 = x 1 , X 2 = x 2 , ⋯ , X n = x n } = P { X 1 = x 1 } P { X 2 = x 2 } ⋯ P { X n = x n } = P { X = x 1 } P { X = x 2 } ⋯ P { X = x n } L=P\{X_1=x_1,X_2=x_2,\cdots,X_n=x_n\}=P\{X_1=x_1\}P\{X_2=x_2\}\cdots P\{X_n=x_n\}=P\{X=x_1\}P\{X=x_2\}\cdots P\{X=x_n\} L=P{X1=x1,X2=x2,⋯,Xn=xn}=P{X1=x1}P{X2=x2}⋯P{Xn=xn}=P{X=x1}P{X=x2}⋯P{X=xn} ;
第二步:对似然函数 L L L 两边取对数 ln L \ln L lnL ;
第三步: (1) 若 ln L \ln L lnL 只含有一个参数 θ \theta θ ,令 d ( ln L ) / d θ = 0 d(\ln L)/d\theta=0 d(lnL)/dθ=0 ,解出驻点 θ ^ = θ ^ ( x 1 , x 2 , ⋯ , x n ) \widehat{\theta}=\widehat{\theta}(x_1,x_2,\cdots,x_n) θ =θ (x1,x2,⋯,xn)(估计值),从而可以得到最大似然估计量 θ ^ = θ ^ ( X 1 , X 2 , ⋯ , X n ) \widehat{\theta}=\widehat{\theta}(X_1,X_2,\cdots,X_n) θ =θ (X1,X2,⋯,Xn) ;
(2)若 ln L \ln L lnL 含有两个参数 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2 ,令 ∂ ln L / ∂ θ 1 = 0 , ∂ ln L / ∂ θ 2 = 0 \partial \ln L/\partial \theta_1=0,\partial \ln L/\partial \theta_2=0 ∂lnL/∂θ1=0,∂lnL/∂θ2=0 ,解出驻点即可得到估计值。
C a s e I I : \pmb{Case\space II:} Case II: 总体 X X X 为连续型(概率密度 f ( x ) f(x) f(x) 已知,但含有未知参数)
第一步:似然函数 L = f ( x 1 ) f ( x 2 ) ⋯ f ( x n ) ; L=f(x_1)f(x_2)\cdots f(x_n); L=f(x1)f(x2)⋯f(xn); 其余步骤同上。
【例】设总体 X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma^2) X∼N(μ,σ2) , ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) 为来自总体的简单随机样本。设 μ = 2 \mu=2 μ=2 ,求参数 σ 2 \sigma^2 σ2 的矩估计量。
解: 似然函数为 L = f ( x 1 ) f ( x 2 ) ⋯ f ( x n ) = ( 1 2 π ) n ⋅ ( σ 2 ) − n 2 E X P { − 1 2 σ 2 ∑ i = 1 n ( x i − 2 ) 2 } . L=f(x_1)f(x_2)\cdots f(x_n)=\big(\frac{1}{\sqrt{2\pi}}\big)^n\cdot (\sigma^2)^{-\frac{n}{2}}EXP\big\{-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-2)^2\big\}. L=f(x1)f(x2)⋯f(xn)=(2π1)n⋅(σ2)−2nEXP{−2σ21i=1∑n(xi−2)2}. ln L = n ln ( 1 2 π ) − n 2 ln σ 2 − 1 2 σ 2 ∑ i = 1 n ( x i − 2 ) 2 . \ln{L}=n\ln\big(\frac{1}{\sqrt{2\pi}}\big)-\frac{n}{2}\ln\sigma^2-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-2)^2. lnL=nln(2π1)−2nlnσ2−2σ21i=1∑n(xi−2)2. 令 d ln L d ( σ 2 ) = − n 2 1 σ 2 + 1 2 σ 4 ∑ i = 1 n ( x i − 2 ) 2 = 0 \frac{d\ln L}{d(\sigma^2)}=-\frac{n}{2}\frac{1}{\sigma^2}+\frac{1}{2\sigma^4}\sum_{i=1}^n(x_i-2)^2=0 d(σ2)dlnL=−2nσ21+2σ41i=1∑n(xi−2)2=0 可解得 σ 2 \sigma^2 σ2 的最大似然估计量为: σ ^ 2 = 1 n ∑ i = 1 n ( x i − 2 ) 2 . \widehat{\sigma}^2=\frac{1}{n}\sum_{i=1}^n(x_i-2)^2. σ 2=n1i=1∑n(xi−2)2.
写在最后
以上便是用点估计法对总体分布的参数进行近似的方法,既然只是估计,那肯定会有误差,到底我们这样估计好不好呢,下一篇文章我们来学习参数估计量的评价标准。
相关文章:
)
【考研数学】概率论与数理统计 —— 第七章 | 参数估计(1,基本概念及点估计法)
文章目录 引言一、参数估计的概念二、参数的点估计2.1 矩估计法2.2 最大似然估计法 写在最后 引言 我们之前学了那么多分布,如正态分布 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2),泊松分布 P ( λ ) P(\lambda) P(λ) 等等,都是在已知 …...

获取文本长度
使用TextView的getLineCount方法,它可以返回TextView当前显示的行数。但是,这个方法只有在TextView绘制完成后才能返回正确的值,否则可能返回0。因此,需要在TextView的post方法中调用,或者在onWindowFocusChanged方法中…...
python html(文件/url/html字符串)转pdf
安装库 pip install pdfkit第二步 下载程序wkhtmltopdf https://wkhtmltopdf.org/downloads.html 下载7z压缩包 解压即可, 无需安装 解压后结构应该是这样, 我喜欢放在项目里, 相对路径引用(也可以使用绝对路径, 放其他地方) import pdfkit# 将 wkhtmltopdf.exe程序 路径 p…...

Spring概述
Spring概述 Spring 是最受欢迎的企业级 Java 应用程序开发框架,数以百万的来自世界各地的开发人员使用 Spring 框架来创建性能好、易于测试、可重用的代码。 Spring 框架是一个开源的 Java 平台,它最初是由 Rod Johnson 编写的,并且于 2003 …...

Linux网卡
网卡 网卡(Network Interface Card,NIC)是一种计算机硬件设备,也称为网络适配器或网络接口控制器。一个网卡就是一个接口 网卡组成和工作原理参考https://blog.csdn.net/tao546377318/article/details/51602298 每个网卡都拥有唯…...

【Python机器学习】零基础掌握ElasticNet变量选择回归器
如何优雅地解决房价预测问题? 房价预测一直是一个热门而复杂的话题。假设一个地产商希望准确地预测不同城市区域的房价,以便更有效地进行房地产投资。问题在于,房价是由多种因素共同决定的,例如地段、房屋面积、交通便利程度等。 为了解决这个问题,一个可行的思路是使用…...

【数据结构】模拟实现Vecotr
namespace my_vector {template <class T>class vector{public:typedef T* iterator;typedef const T* const_iterator;//常量指针,指针指向的值不可以变;//构造函数vector():start(nullptr),finish(nullptr),end_of_storage(nullptr){}//析构函数…...

Qt开发: 利用Qt的charts模块绘制曲线、饼图、柱状图、折线图等各种图表
一、前言 Qt Charts模块是Qt提供的一个用于创建各种类型图表的功能模块。为开发人员提供了一种简单而强大的方式来可视化数据。Qt Charts模块基于Qt GUI框架构建,可以与其他Qt模块无缝集成,例如Qt Widgets、Qt Quick和Qt OpenGL。 Qt Charts模块包含了几个核心类: (1)Q…...
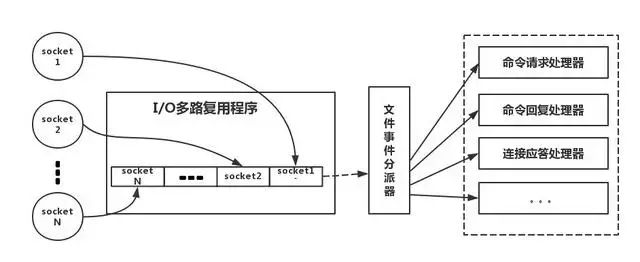
Redis:加速你的应用响应时间,提升用户体验
绝大部分写业务的程序员,在实际开发中使用 Redis 的时候,只会 Set Value 和 Get Value 两个操作,对 Redis 整体缺乏一个认知。这里对 Redis 常见问题做一个总结,解决大家的知识盲点。 1、为什么使用 Redis 在项目中使用 Redis&am…...

乐鑫 SoC 内存映射入门
微控制器 (MCU) 的性能和内存能力逐步提升,其复杂度也随之加大。特别是当用户需要配置内存管理单元来映射外部存储器芯片 (Flash/SPIRAM) 时,这种现象尤其明显。 开始在乐鑫 SoC 上运行 Zephyr RTOS 时,会发现这些 SoC 与 ARM 架构的 MCU 相…...
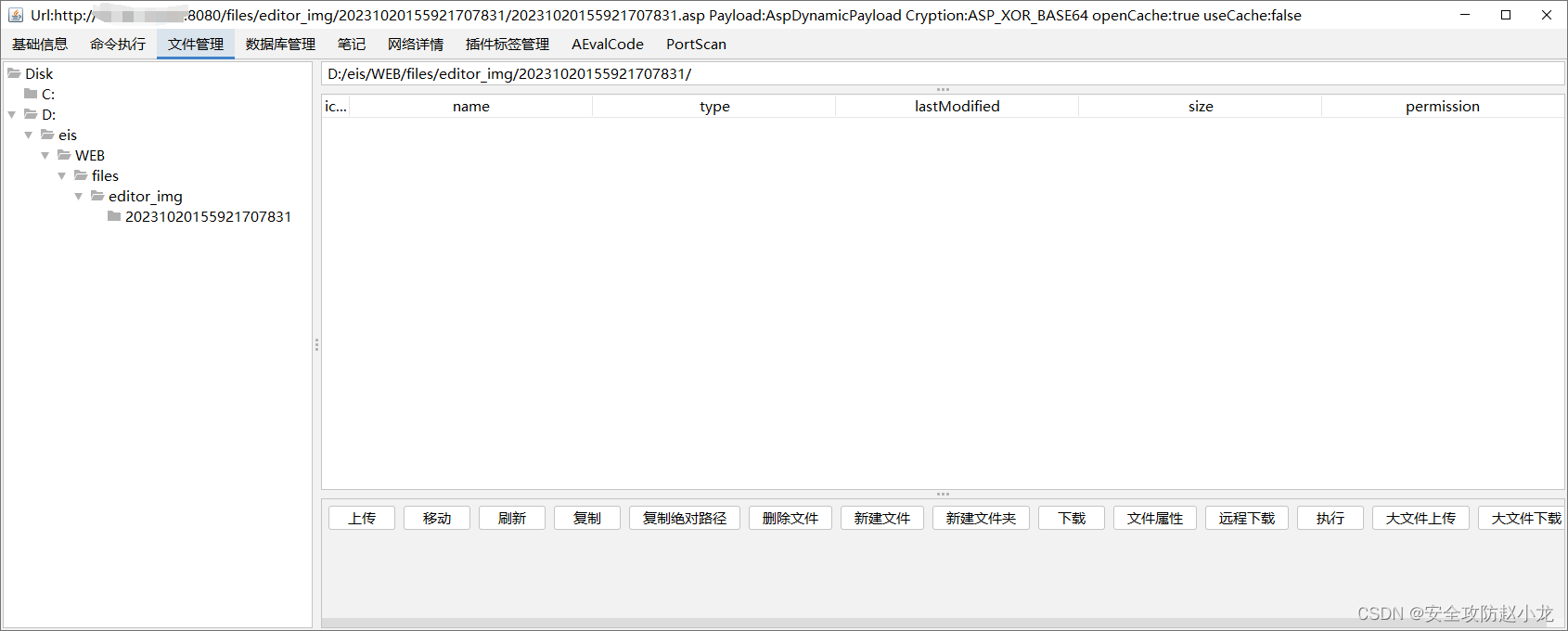
蓝凌EIS智慧协同平台saveImg接口存在任意文件上传漏洞
蓝凌EIS智慧协同平台saveImg接口存在任意文件上传漏洞 一、蓝凌EIS简介二、漏洞描述三、影响版本四、fofa查询语句五、漏洞复现六、深度复现1、发送如花2、哥斯拉直连 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者…...

【SEC 学习】美化 Linux 终端
一、步骤 1. 进入 /etc/bash.bashrc vim /etc/bash.bashrc2. 重新加载 bash.bashrc source /etc/bash.bashrc二、各参数指标 符号含义\u当前用户的账号名称\h仅取主机的第一个名字,如上例,则为fc4,.linux则被省略\H完整的主机名称。例如&…...

【Unity小技巧】可靠的相机抖动及如何同时处理多个震动(附项目源码)
文章目录 每篇一句前言安装虚拟相机虚拟相机震动测试代码控制震动清除震动控制震动的幅度和时间 两个不同的强弱震动同时发生源码完结 每篇一句 围在城里的人想逃出来,站在城外的人想冲进去,婚姻也罢,事业也罢,人生的欲望大都如此…...
)
【51单片机】51单片机概述(学习笔记)
一、课程简介 1、硬件设备 51单片机开发板 Win电脑 2、软件设备 Keil5:编写程序代码 STC-ISP:下载程序 有道词典 福昕阅读器 二、开发工具介绍 1、Keil5 keil.com > 下载C51版本 > 使用破解程序 2、STC-ISP 绿色版:直接运…...

make和new的区别
make和new都是golang用来分配内存(理论上都是在堆上分配),不同的是 new分配空间只是将内存清零,并没有初始化;而make分配之后只初始化内存new为每个类型都分配,而make专用于slice、map、channew返回类型指…...

vue3获取页面路径
import { useRouter, useRoute } from vue-routerconst router useRouter()router.currentRoute.value.path // 页面路径...

基于STM32闭环步进电机控制系统设计
**单片机设计介绍,1654基于STM32闭环步进电机控制系统设计(仿真,程序,说明) 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序文档 六、 文章目录 一 概要 基于STM32的闭环步进电机控制系统设计是…...

Java中的队列:各种类型及使用场景
在Java中,队列是一种重要的数据结构,用于存储按特定顺序排列的元素。队列在多线程环境中特别有用,因为它们可以用来解决并发问题。在Java中,队列主要分为以下几种类型: 接口: Queue: 这是Java Queue接口&…...

MappingMongoConverter原生mongo 枚举类ENUM映射使用的是name
j.l.IllegalArgumentException: No enum constant com.xxx.valobj.TypeEnum.stringat java.lang.Enum.valueOf...

Java中的锁:类型,比较,升级与降级
在Java中,锁是一种用于实现并发控制的重要工具。在多线程环境中,锁可以确保数据的一致性和完整性。Java提供了多种类型的锁,包括内置的synchronized关键字,ReentrantLock类以及更高级的并发工具,如StampedLock和ReadWr…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
